IAP 2022: Advanced Optimization Session (Session 2)¶
Shuvomoy Das Gupta
Basic Integer Programming¶
Example: Shuvo's COVID isolation¶
It is Summer of 2020. Shuvo, unfortunately, gets infected with COVID 19. So he has to isolate in a secure place designated by authority. Now he can take some valuable items with him during the isolation phase. He has $N$ items, each with a weight $w_i$ and a price $p_i$. Because he is feeling weak, he can only carry $C$ kilos. How does he choose what to bring with him so as to maximize the total value?
We can model Shuvo's situation as a (pure) integer optimization problem:
\begin{align*} \max& \sum_{i=1}^N v_i x_i \\ \text{s.t.}& \sum_{i=1}^N w_i x_i \leq C \\ & x_i \in \{0,1\}^n, \quad i = 1,\ldots,N \end{align*}Variable $x_i$ expresses if item $i$ is selected or not. In generally this problem is called the $0-1$ knapsack problem.
using JuMP, Gurobi, LinearAlgebra
# Problem data
v = [9, 3, 2, 6, 10, 7, 6, 6, 4, 5, 4, 1, 1,
6, 3, 2, 3, 2, 10, 7, 9, 8, 3, 10, 8, 5,
3, 8, 3, 6, 5, 7, 8, 6, 9, 7, 5, 5, 1, 5,
9, 5, 4, 5, 5, 3, 4, 8, 8, 10]
w = [4, 10, 9, 8, 8, 4, 7, 3, 1, 10, 5, 4, 2,
3, 9, 9, 9, 5, 8, 8, 4, 2, 6, 10, 5, 7, 7,
8, 4, 7, 7, 8, 4, 4, 10, 3, 9, 2, 9, 10, 3,
7, 3, 5, 5, 7, 10, 10, 5, 8]
C = 50
n = length(v)
50
Add the variable $x$ along with the binary constraint.
knapsack_model = Model(Gurobi.Optimizer)
Set parameter TokenServer to value "flexlm"
A JuMP Model Feasibility problem with: Variables: 0 Model mode: AUTOMATIC CachingOptimizer state: EMPTY_OPTIMIZER Solver name: Gurobi
# I am turing these off just for illustration,
# otherwise Gurobi ends up solving the problem during the presolve phase 😲
set_optimizer_attribute(knapsack_model, "Presolve", 0)
set_optimizer_attribute(knapsack_model, "Heuristics", 0)
Set parameter Presolve to value 0 Set parameter Heuristics to value 0
@variable(knapsack_model, x[1:n] >= 0, Bin)
50-element Vector{VariableRef}:
x[1]
x[2]
x[3]
x[4]
x[5]
x[6]
x[7]
x[8]
x[9]
x[10]
x[11]
x[12]
x[13]
⋮
x[39]
x[40]
x[41]
x[42]
x[43]
x[44]
x[45]
x[46]
x[47]
x[48]
x[49]
x[50]
Add the objective $v^\top x$.
@objective(knapsack_model, Max, v' * x)
Add the constraint $w^\top x \leq C$.
@constraint(knapsack_model, w' * x <= C)
optimize!(knapsack_model)
Set parameter Heuristics to value 0
Set parameter Presolve to value 0
Gurobi Optimizer version 9.5.0 build v9.5.0rc5 (linux64)
Thread count: 48 physical cores, 96 logical processors, using up to 32 threads
Optimize a model with 1 rows, 50 columns and 50 nonzeros
Model fingerprint: 0x0c089da8
Variable types: 0 continuous, 50 integer (50 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+01]
Objective range [1e+00, 1e+01]
Bounds range [0e+00, 0e+00]
RHS range [5e+01, 5e+01]
Variable types: 0 continuous, 50 integer (50 binary)
Root relaxation: objective 1.040000e+02, 1 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
* 0 0 0 104.0000000 104.00000 0.00% - 0s
Explored 1 nodes (1 simplex iterations) in 0.01 seconds (0.00 work units)
Thread count was 32 (of 96 available processors)
Solution count 1: 104
Optimal solution found (tolerance 1.00e-04)
Best objective 1.040000000000e+02, best bound 1.040000000000e+02, gap 0.0000%
User-callback calls 36, time in user-callback 0.00 sec
println(abs.(value.(x)))
[1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0]
objective_value(knapsack_model)
104.0
Branch-and-bound algorithm: the key algorithm to solve discrete-valued problem¶
Integer optimization problems in solvers such are Gurobi are solved using the Branch-and-bound algorithm. Let us try to understand how the basic Branch-and-bound algorithm works through a running example.
Toy example¶
In particular, consider the following (small) knapsack problem:
\begin{align*} \max\:& x + y \\ \text{s.t.}\:& x + 2y \leq 1.5 \\ & x, y \in \{0,1\} \end{align*}How would you solve this?
small_knapsack_model = Model(Gurobi.Optimizer)
@variable(small_knapsack_model , x, Bin)
@variable(small_knapsack_model , y, Bin)
@constraint(small_knapsack_model , x+2*y<=1.5)
@objective(small_knapsack_model , Max, x+y)
optimize!(small_knapsack_model )
println("X is: ", value(x), " Y is: ", value(y))
Set parameter TokenServer to value "flexlm" Gurobi Optimizer version 9.5.0 build v9.5.0rc5 (linux64) Thread count: 48 physical cores, 96 logical processors, using up to 32 threads Optimize a model with 1 rows, 2 columns and 2 nonzeros Model fingerprint: 0x062dc61b Variable types: 0 continuous, 2 integer (2 binary) Coefficient statistics: Matrix range [1e+00, 2e+00] Objective range [1e+00, 1e+00] Bounds range [0e+00, 0e+00] RHS range [2e+00, 2e+00] Found heuristic solution: objective 1.0000000 Presolve removed 1 rows and 2 columns Presolve time: 0.00s Presolve: All rows and columns removed Explored 0 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units) Thread count was 1 (of 96 available processors) Solution count 1: 1 Optimal solution found (tolerance 1.00e-04) Best objective 1.000000000000e+00, best bound 1.000000000000e+00, gap 0.0000% User-callback calls 139, time in user-callback 0.00 sec X is: 1.0 Y is: 0.0
Branch and Bound Tree¶
The simple way is just to consider each possible value for $x$ and $y$ and compare the cost.
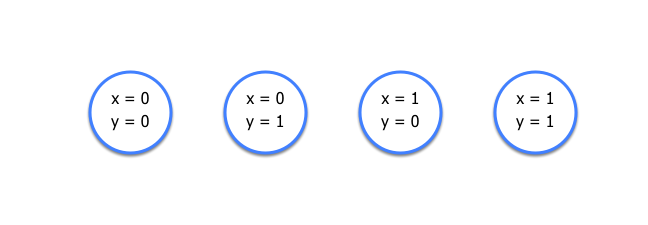
In the general case, this would lead to $2^N$ possible collections of items. After Shuvo has weighed all of them (and verified that he can lift them at once), he just chooses the best set.
Let's visualize this approach as a search tree:
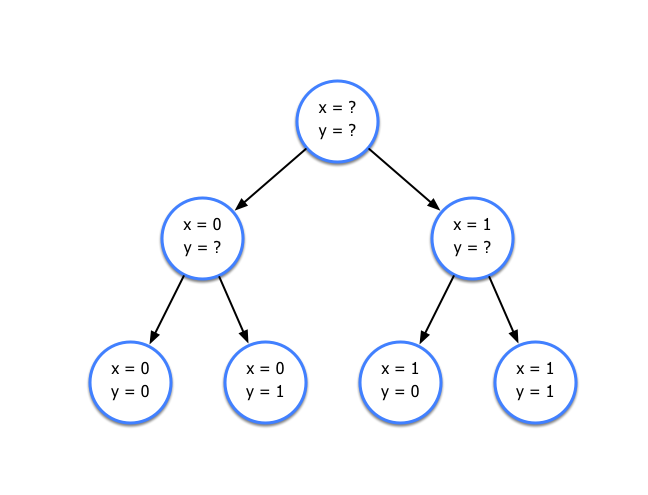
It's rooted at what we call the relaxation: none of variables have integrality enforced. As we go down leaves of the tree, we add pick a variable to branch on, and create two descended nodes that fix that variable to one of its possible values. If we follow the tree all the way to the bottom, we reach our enumeration from before.
As we go down the arcs of the tree we restrict our problem more and more, we must have that:
If node
qis descended from nodep, we must have that the optimal cost of subproblemqcannot be better than that of nodep
When we are solving the subproblem q: the following possibilities can happen:
(i) subproblem q is leads to an infeasible solution, so q and any of its descendents cannot contain the optimal solution => we can discard it
(ii) subproblem q has an optimal value that is worse than our best found feasible solution so far, so q and any of its descendents cannot contain the optimal solution => we can discard it
(iii) none of (i), (ii) happens, so we need to continue branching on q (create more descendents of q)
That is, we can prune the tree and safely discard some nodes, kind of like this:
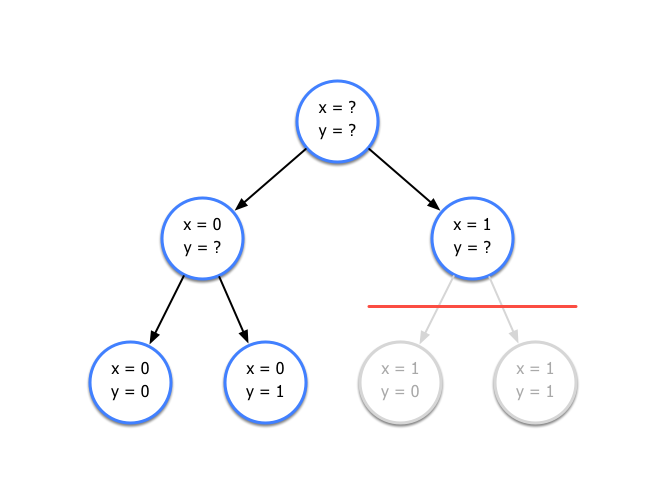
So at the root node the solver is solving the following relaxation:
\begin{align*} \max\quad& x + y \\ \text{s.t.}\quad& x + 2y \leq 1.5 \\ & 0 \leq x, y \leq 1 \\ & x, y \in \{0,1\} \end{align*}and subsequently restricting the problem more and more at the descendents.
What does the relaxation (no integrality restrictions) of this problem look like?
- First, we solve the LP relaxation and get $(x^*,y^*) = (1,0.25)$.
- This isn't integer feasible, so we branch on $y$. The subproblem with $y = 1$ is infeasible, and the subproblem with $y = 0$ is feasible with solution $(x^*,y^*) = (1,0)$. This is integer feasible, so we update our lower bound. We've also exhausted the tree, so we have our optimal solution!
- The branch-and-bound scheme can end up solving many subproblems, so for it to work well, we need to prune large portions of the tree.
Basic operation of the branch-and-bound algorithm¶
For a maximization problem, we'll keep track of a global lower bound $LB$ for our problem. Each node q will have an upper bound $UB_q$ that it inherents from its parent. If we get to the point where we have solved all subproblems (or, ideally, pruned off a great deal of them), we know that we're optimal. To do this we'll also keep track of a list $L$ of subproblems left to solve; initially, it's just the relaxation. The procedure is:
While $L$ is not empty, pick a subproblem q out of our list $L$ and solve it.
ifqis infeasible,continueifthe solution is integer feasible, update the lower bound $LB$ if the cost is higher than what we had beforeifthe relaxation value is less than our global $LB$continueelsepick a non-integer variable $i$ and branch by adding two subproblems to $L$:- One with $x_i = 0$
- Another with $x_i = 1$
Branch-and-bound is sometimes called an implicit enumeration scheme because of step 3: we avoid solving any subproblems that we can prove won't produce the optimal solution.
For a minimization problem, the role of upper bound and lower bound will be flipped.
Ιmplementation of the Branch and Bound Algorithm in Gurobi¶
The "magic" of modern MIP solvers largely comes down to pruning massive portions of the tree. Some of this is essentially beyond your control, but there are certain things which you can do. This is the topic of Part II of this IP crash course.
In what follows, we focus on Gurobi, a commercial solver that solves Mixed Integer LPs/QPs/QCQPs. (You can get the full picture of what solvers JuMP supports and what types of problems you can solve with each of them by visiting http://www.juliaopt.org/JuMP.jl/latest/installation/ and scrolling a bit down.)
What are the ingredients of Gurobi's branch and bound implementation?
- Presolve: reduce problem size via removal of redundant constraints and variable substitutions.
- Sophisticated Implementations of Continuous Optimization Methods: simplex-based, barrier-based.
- Cutting Planes: over the course of the solution process, add cuts that tighten the model and remove potential undesired fractional solution.
- Heuristics: e.g., randomized rounding.
- Branch Variable Selection: which variable to branch on.
Gurobihas lot of internal heuristics to do it.
Understanding Gurobi's Output¶
Usually Gurobi starts with solves the LP relaxation and reports back:
Root relaxation: objective 4.014179e+00, 18 iterations, 0.00 seconds
Now it explores the branch-and-bound tree, and updates us as it goes along. Let's look at just the first line:
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 4.01418 0 7 2.35937 4.01418 70.1% - 0s
We see that the information is broken down into four main columns:
Nodes: Global node information- how many nodes have we looked at
- how many do we have in our queue
Current Node- objective
- depth in the tree
- number of noninteger variables in the solution
Objective Bounds- Best incumbent
- bound at the node (by solving the relaxation)
- the gap between the two
Work- average simplex iterations per node
- total elapsed time
Solver Parameters¶
Gurobi (and other high-quality solvers such as CPLEX) allow you to tweak a wide range of different parameters; sometimes tuning these can drastically improve performance. It can be kind of intimidating, though: Gurobi has over 100 parameters (and CPLEX has even more!), so which are the important ones?
Some useful ones:
Gurobi:
TimeLimit: how long the solver will run before giving upMIPGap: termination criterion for relative gap $\frac{UB-LB}{LB}$MIPFocus: High-level controls on solver priority (proving optimality or increasing bound or finding optimal solution)VarBranch: MIP branching strategy (pseudocost/strong branching)Cuts: How aggresive we want to be in our cut generation (higher values improve lower bound but might slow overall process).
How to set these parameters in JuMP 0.22?
set_optimizer_attribute(model, "TimeLimit", 100)
set_optimizer_attribute(model, "Presolve", 0)
Is that it? Well, no, but you probably need domain knowledge about your problem to go much further.
Mixed-integer programming (MIP)¶
Mixed-integer programing problems are similar to integer programming problem but only some variables are integer-valued, where the rest are real-valued. The standard form MIP is defined as:
$$ \begin{aligned} & \text{minimize} && c^T x + d^T y\\ & \text{subject to} && A x + B y= f \\ & && x \geq 0, y \geq 0 \\ & && x \in \mathbb{R}^n, y \in {\{0,1\}}^p, \end{aligned} $$where $x,y$ are the decision variables, and the problem data is $A \in \mathbb{R}^{m \times n}, B \in \mathbb{R}^{m \times p}, c \in \mathbb{R}^n, d \in \mathbb{R}^p, f \in \mathbb{R}^m$.
Situations where mixed-integer programming models show up¶
Usually shows up in situations where
- modeling do/don't do decisions
- logical conditions
- implications (if something happens do this)
- either/or
Modeling "or" condition using MIP¶
Modeling logical or statements:
If we have a constraint such as: $$ \bigvee_{i=1,\ldots,m}(a_{i}^{\top}x\geq b_{i}), $$ which means atleast one of $\{a_{i}^{\top}x\geq b_{i}\}_{i\in\{1,\ldots,m\}}$. We model this through big-M constraint as follows:
\begin{align*} & y_{i}\in\{0,1\},\; \quad i=1,\ldots,m,\\ & a_{i}^{\top}x\geq b_{i}-M(1-y_{i}),\; \quad i=1,\ldots,m,\\ & \sum_{i=1}^{m}y_{i}\geq1. \end{align*}Here the big-M is assumed to be a very large positive number. The variable $y_{i}$ corresponds to the activation of the constraint $a_{i}^{\top}x\geq b_{i}$. Say, $y_{j}=1$ then $a_{j}^{\top}x\geq b_{j}-M(1-y_{j})=b_{j}$ which means that the constraint $a_{j}^{\top}x\geq b_{j}$ is activated. Note that the system of inequalities ensure that atleast one of the $y_{i}$s will be $1$, hence atleast one of $a_{i}^{\top}x\geq b_{i}$ will be activated.
Modeling implication statment:¶
Remember that the logical argument $P\Rightarrow Q$ is equivalent to $\lnot P\vee Q$ (``not $P$'' or Q), \emph{i.e.}, atleast one of $Q$ or $\lnot P$ will happen.
So $a^{\top}x\geq b\Rightarrow d^{\top}x\geq f$ is equivalent to
\begin{align*} & \lnot(a^{\top}x\geq b)\vee(d^{\top}x\geq f)\\ \Leftrightarrow & (a^{\top}x<b)\vee(d^{\top}x\geq f)\\ \Leftrightarrow & (a^{\top}x\leq b-\epsilon)\vee(d^{\top}x\geq f)\\ \Leftrightarrow & (-a^{\top}x\geq-b+\epsilon)\vee(d^{\top}x\geq f), \end{align*}where $\epsilon$ is a very small positive number. Then we proceed in a similar fashion for modeling ``or'' statements.
Solving MIP using JuMP+Gurobi¶
Let's see one simple example of how to solve MIP using JuMP+Gurobi. We will solve the standard form MIP:
# Load the data
include("img//mip_data.jl");
println(f)
[1.6760336777741285, 1.3832989003608955, 2.797511333830128, -2.6463111345930477, 0.5484362297666834, -6.031736504363563, 6.562664781641179, -3.2098566996858806, -2.762580590875767, 2.4686403945076987, 1.664406125871585, 2.426813022758185, 7.761292956425351]
using JuMP, Gurobi
sfMipModel = Model(Gurobi.Optimizer)
Set parameter TokenServer to value "flexlm"
A JuMP Model Feasibility problem with: Variables: 0 Model mode: AUTOMATIC CachingOptimizer state: EMPTY_OPTIMIZER Solver name: Gurobi
set_optimizer_attribute(sfMipModel, "MIPFocus", 3)
# If you are more interested in good quality feasible solutions, you can select MIPFocus=1.
# If you believe the solver is having no trouble finding the optimal solution, and wish to focus more
# attention on proving optimality, select MIPFocus=2.
# If the best objective bound is moving very slowly (or not at all), you may want to try MIPFocus=3 to focus on the bound.
Set parameter MIPFocus to value 3
@variable(sfMipModel, x[1:n] >=0)
15-element Vector{VariableRef}:
x[1]
x[2]
x[3]
x[4]
x[5]
x[6]
x[7]
x[8]
x[9]
x[10]
x[11]
x[12]
x[13]
x[14]
x[15]
@variable(sfMipModel, y[1:p] >= 0, Bin)
14-element Vector{VariableRef}:
y[1]
y[2]
y[3]
y[4]
y[5]
y[6]
y[7]
y[8]
y[9]
y[10]
y[11]
y[12]
y[13]
y[14]
@objective(sfMipModel, Min, sum(c[i] * x[i] for i in 1:n)+sum(d[i]*y[i] for i in 1:p))
for i in 1:m
@constraint(sfMipModel, sum(A[i,j]*x[j] for j in 1:n)+ sum(B[i,j]*y[j] for j in 1:p) == f[i])
end
optimize!(sfMipModel)
Set parameter MIPFocus to value 3
Gurobi Optimizer version 9.5.0 build v9.5.0rc5 (linux64)
Thread count: 48 physical cores, 96 logical processors, using up to 32 threads
Optimize a model with 13 rows, 29 columns and 377 nonzeros
Model fingerprint: 0x283aaa28
Variable types: 15 continuous, 14 integer (14 binary)
Coefficient statistics:
Matrix range [6e-03, 3e+00]
Objective range [4e-02, 2e+00]
Bounds range [0e+00, 0e+00]
RHS range [5e-01, 8e+00]
Presolve time: 0.00s
Presolved: 13 rows, 29 columns, 360 nonzeros
Variable types: 15 continuous, 14 integer (14 binary)
Root relaxation presolved: 13 rows, 29 columns, 360 nonzeros
Root relaxation: objective 6.576195e+00, 19 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 6.57620 0 5 - 6.57620 - - 0s
H 0 0 11.8611889 7.95094 33.0% - 0s
0 0 9.48852 0 4 11.86119 9.48852 20.0% - 0s
H 0 0 11.4692035 9.48852 17.3% - 0s
Cutting planes:
Gomory: 10
Lift-and-project: 1
MIR: 14
Flow cover: 24
Inf proof: 3
Explored 1 nodes (27 simplex iterations) in 0.07 seconds (0.02 work units)
Thread count was 32 (of 96 available processors)
Solution count 2: 11.4692 11.8612
Optimal solution found (tolerance 1.00e-04)
Best objective 1.146920353965e+01, best bound 1.146920353965e+01, gap 0.0000%
User-callback calls 236, time in user-callback 0.00 sec
x_sol = value.(x)
15-element Vector{Float64}:
0.9899474320258836
0.9642308227536968
0.5868159949777088
0.4630020993740819
0.901053837606137
0.5631434853865587
0.2257929580263573
0.6532009804572236
1.5223238215506862
0.0
0.54943253051681
1.1917506578662456
0.0
0.8500168300331316
0.8154952228571157
y_sol = value.(y)
14-element Vector{Float64}:
-0.0
-0.0
1.0
1.0
-0.0
-0.0
1.0
-0.0
-0.0
1.0
1.0
-0.0
-0.0
-0.0
Speed up the default Gurobi solver by exploiting problem structure¶
Gurobi's solver, while very good, is a generic solver, and is not intelligent enough to exploit problem specific insights. So, if you have specific domain knowledge for the problem you are trying to solve, you need to tell Gurobi about it, which will speed up the process by orders of magnitude.
There are 4 ways to provide Gurobi with problem specific insights in JuMP.
- Lazy constraint
- User cuts
- Custom heuristic
- Warm-starting
Lazy constraint¶
- Lazy constraint: Lazy constraints are useful when the full set of constraints is too large to explicitly include in the initial formulation. When a MIP solver reaches a new solution, for example with a heuristic or by solving a problem at a node in the branch-and-bound tree, it will give the user the chance to provide constraints that would make the current solution infeasible.
Suppose your integer optimization problem is:
\begin{array}{ll} \underset{x\in\mathbf{R}^{d}}{\mbox{minimize}} & c^\top x \\ \mbox{subject to} & Ax \leq b,\\ & x\succeq0,\\ & d_{i}^{\top}x\leq h_{i},\quad i=1,\ldots,p,\\ & x\in\{0,1\}^{d}, \end{array}where $p$ is a very large number. In fact it does happen in medical imaging. So, in this case, the problem starts with
\begin{array}{ll} \underset{x\in\mathbf{R}^{d}}{\mbox{minimize}} & c^\top x \\ \mbox{subject to} & Ax \leq b,\\ & x\succeq0,\\ & x\in\{0,1\}^{d}, \end{array}and once a integer solution is reached, we check if the solution violates any of the constraints $\{d_{i}^{\top}x\leq h_{i}\}_{i=1}^{p}$ and add the first one that gets violated. This can be done through the following code:
function good_callback_function(cb_data)
x_current = callback_value.(x)
if x_current violates some condition "conV"
con = @build_constraint(x should not violate "conV")
MOI.submit(model, MOI.LazyConstraint(cb_data), con)
end
end
# data
n = 20
p = 5
m = 5
A = [-0.25149258982896966 0.525287826731042 -0.6656342865169662 -1.2960398772338568 0.9101252450751471 -0.07298248406603706 -1.9148704340623688 -0.5073995272298952 -1.6558511941286744 2.1006659624182586 -0.502359026079171 -0.1708406495941207 1.4161030569819415 0.33735905844690145 -0.10748103771152817 -1.4416340194991104 -0.9578960880328228 -0.1738984790022571 -1.0517643292393826 -0.8271987403702172; -0.8518984622275042 -1.374417162491773 0.35920232369365845 0.8437691247979793 -0.6281577605465152 0.5921264379488904 -0.12756078132890084 -0.44447204507515287 0.7293549470299907 0.715267254601397 -0.9155882952842251 0.35378971887340743 -0.8043683142766567 0.5324223554306367 0.2088297149344946 -0.5594219995662968 0.5632674521223371 -0.2302672262989066 0.7676987968759004 1.0910836780489503; 1.473815753336459 -0.6525879104965642 0.8519411939583414 -0.05756789248416348 -0.7125581880426727 0.4736057460760701 -2.231011632648033 0.5409490591899032 0.1583459153748212 -1.1509507228336586 1.3994115761547934 0.14111034486559706 -0.15123003344570538 -0.547672888665602 -1.9555427017941476 -1.8533179907378834 0.13798098584535193 0.2337797562353011 -0.8404137158789987 0.060446173222487264; 0.6396537082966063 0.856847789735652 1.4805326346158039 0.012324563610194187 1.3977381658753554 1.3342059688961259 -0.4784014905808825 -0.14890693050929457 0.8155899237370289 -0.5697405099766946 1.3446291535605297 0.6840341944716634 1.2484251582871324 1.2891201777341281 -0.2791170028219365 0.43803145770984425 0.4677466100676112 1.3639772554672074 0.8359137382225728 0.8723882764319004; 0.40517145458826054 1.169967487661965 1.7941045258417871 1.035188318563306 1.118495812473751 -0.04027314052794962 0.5438620238342292 -0.8181792084120169 0.08209406151847103 0.6469386439823567 -0.9467882212470308 -0.2866858366079981 0.8836746919594078 -2.0164799655225094 -0.42541330025958685 -0.09145359012880407 0.8920741578367347 -0.5093214870138416 -0.23118339134915017 -1.262095251923206]
D = [-2.0831200526934572 1.5615062392183003 0.18155475431473142 0.7599664330346061 0.2668125999785801 1.2573917809432806 0.04093911087719557 -0.21735884773163816 1.6340683454668137 1.2804063399285137 0.6443447646682994 -0.8939206481655969 -0.22507735354054656 -0.3094500241639488 0.2954219652735186 -0.3880055556581179 -0.9578091110001216 -0.922838957226308 -1.3571981131817064 -0.05064205091038371; 0.6324558903791979 -0.6652227624026216 -1.7276813422697317 -0.689479323056671 -0.7816950255371095 -1.802372714658206 0.14164169531740856 0.46527545010854515 1.1036334528775311 1.305688755430216 0.3797915504580763 1.7602878854059907 0.8155022785101097 -0.6315798865662005 -0.30581893855662595 -0.33305541977514697 -0.8854550960099433 0.03621076189783246 -0.2788693026530316 1.6348184993843053; -2.4242492532538096 0.5770923004878816 0.4961795092913091 -0.04867957395223246 0.6673192113922586 -0.8855274251005092 0.4568856956106312 -0.6097467636667095 -0.3639368866683512 0.5625062854293676 -0.5017933052998168 0.3836052143475206 1.8936021566371188 -0.209665904941543 -1.3278566925429307 0.6736435837748775 -0.5017805315844522 0.6452850279162458 0.7881379044649098 0.45931063639065656; -0.5372061672955294 -0.7867658024064041 0.09657107558669714 -1.0587831441218194 -1.2444111679260363 -0.6885359430850223 -0.4325022650433149 0.7912025990048928 0.1141092892049688 0.918388681602774 0.41101551577580714 1.3817408040581836 -0.030696867637192395 0.7523799268172908 -0.3083505028779359 0.27074896029609724 -0.5303233440211375 -1.1025104074431078 -2.3234729621969272 0.705781546034252; 0.6313935384296541 0.699436081582457 -0.5461167811714385 -0.5108885871403681 -1.59867913729006 -0.7350106637365103 -1.1033454910986003 0.898936477156721 -0.07365263955313238 -0.48330570412807555 1.0944353481674236 0.19009504425867302 -0.5106409146420512 0.647369019147565 -0.40169454919669595 -0.1575677053433486 1.4977052939251785 -0.39775746600800416 1.821753152147404 0.10823903833322045]
c = [-5.724274247670441; 0.872180569098502; -13.289441619771337; -1.284190729811427; -10.090248808669005; 19.226305603166242; -14.323991615118594; -5.8893709748795615; -9.801477473401599; -2.533420139004128; -4.017671140375999; -12.25747413009963; -6.5234635509559205; -18.204822439044932; 10.759517257360242; -2.678837137470244; 2.6260424150728934; -9.929728378562064; -1.08448828496412; -14.883711771646961]
b = [-7.3620594939851545; 1.2864238748369008; -5.191670678971517; 3.4603990262005064; -0.9930993374575348]
h = [-5.110534843409266; -0.12459704540647681; -2.8197063217437384; -1.9945660953801996; 3.5137561922861824];
# a proper code is as follows:
lazy_model = Model(Gurobi.Optimizer)
@variable(lazy_model, x[1:n], Bin)
for i in 1:m
@constraint(lazy_model, sum(A[i,j]*x[j] for j in 1:n) <= b[i])
end
@objective(lazy_model, Min, sum(c[i] * x[i] for i in 1:n))
# lazy constraint is added through the following callback function
function my_callback_function(cb_data)
# check the status of the solution at the branch-and-bound tree node
status = callback_node_status(cb_data, lazy_model)
if status == MOI.CALLBACK_NODE_STATUS_FRACTIONAL
# if we enter this block then it means that
# `callback_value(cb_data, x)` is not integer (to some tolerance).
# Our lazy constraint generator requires an
# integer-feasible primal solution, so we can add a `return` here.
return
elseif status == MOI.CALLBACK_NODE_STATUS_INTEGER
# `callback_value(cb_data, x)` is integer (to some tolerance).
println("[😁] Current node has an integer solution")
else
@assert status == MOI.CALLBACK_NODE_STATUS_UNKNOWN
# `callback_value(cb_data, x)` might be integer feasible or infeasible,
# in such a case it is best if we call our lazy constraint
# @assert ensures that if the node status is none of the three conditions above,
# then it will throw an error
end
x_val = callback_value.(cb_data, x) # load the value of the interim solution at the node
for i in 1:p
if sum(D[i,j]*x_val[j] for j in 1:n) > h[i] + 1e-6
println("[😻] Submitting $(i)-th constraint d[i]'x <= h[i] as a lazy constraint")
# 💀 note that we using x_val which is a known vector, not x which is the variable
# also, added a small number 1e-6 to ensure numberical stability
# now add the lazy constraint
con = @build_constraint(sum(D[i,j]*x[j] for j in 1:n) <= h[i])
MOI.submit(lazy_model, MOI.LazyConstraint(cb_data), con) #💀 need to submit the constraint to our model
break
end
end
end
MOI.set(lazy_model, MOI.LazyConstraintCallback(), my_callback_function)
# 💀 need to invoke this command so that JuMP knows that "my_callback_function" is used to generate lazy constraints
optimize!(lazy_model)
Set parameter TokenServer to value "flexlm"
Set parameter LazyConstraints to value 1
Gurobi Optimizer version 9.5.0 build v9.5.0rc5 (linux64)
Thread count: 48 physical cores, 96 logical processors, using up to 32 threads
Optimize a model with 5 rows, 20 columns and 100 nonzeros
Model fingerprint: 0xb04b5cd0
Variable types: 0 continuous, 20 integer (20 binary)
Coefficient statistics:
Matrix range [1e-02, 2e+00]
Objective range [9e-01, 2e+01]
Bounds range [0e+00, 0e+00]
RHS range [1e+00, 7e+00]
[😁] Current node has an integer solution
[😻] Submitting 1-th constraint d[i]'x <= h[i] as a lazy constraint
Presolve time: 0.00s
Presolved: 5 rows, 20 columns, 100 nonzeros
Variable types: 0 continuous, 20 integer (20 binary)
Root relaxation: objective -6.474229e+01, 9 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 -64.74229 0 4 - -64.74229 - - 0s
0 0 -59.68164 0 5 - -59.68164 - - 0s
[😁] Current node has an integer solution
[😻] Submitting 1-th constraint d[i]'x <= h[i] as a lazy constraint
[😁] Current node has an integer solution
* 0 0 0 -48.0618899 -48.06189 0.00% - 0s
Cutting planes:
Gomory: 5
Cover: 3
MIR: 2
StrongCG: 2
RLT: 2
Lazy constraints: 1
Explored 1 nodes (29 simplex iterations) in 0.11 seconds (0.00 work units)
Thread count was 32 (of 96 available processors)
Solution count 1: -48.0619
No other solutions better than -48.0619
Optimal solution found (tolerance 1.00e-04)
Best objective -4.806188988663e+01, best bound -4.806188988663e+01, gap 0.0000%
User-callback calls 116, time in user-callback 0.10 sec
x_sol = value.(x)
20-element Vector{Float64}:
1.0
-0.0
-0.0
1.0
-0.0
-0.0
1.0
1.0
-0.0
-0.0
-0.0
1.0
-0.0
0.9999999999999992
1.0
1.0
1.0000000000000004
0.0
1.0
0.0
println(x_sol[15:20])
[1.0, 1.0, 1.0000000000000004, 0.0, 1.0, 0.0]
sum(x_sol)
10.0
D*x_sol <= h
true
lazy_obj_val = objective_value(lazy_model)
-48.0618898866258
User cuts¶
- User cuts: User cuts, or simply cuts, provide a way for the user to tighten the LP relaxation using problem-specific knowledge that the solver cannot or is unable to infer from the model. Just like with lazy constraints, when a MIP solver reaches a new node in the branch-and-bound tree, it will give the user the chance to provide cuts to make the current relaxed (fractional) solution infeasible in the hopes of obtaining an integer solution.
model = Model(Gurobi.Optimizer)
@variable(model, x <= 10.5, Int)
@objective(model, Max, x)
function my_callback_function(cb_data)
x_val = callback_value(cb_data, x)
con = @build_constraint(x <= floor(x_val))
MOI.submit(model, MOI.UserCut(cb_data), con)
end
MOI.set(model, MOI.UserCutCallback(), my_callback_function)
optimize!(model)
I personally recommend against using user cuts, unless you have a very good idea about the set of integer feasible solutions for your problem.
User cuts must not change the set of integer feasible solutions.
Equivalently, user cuts can only remove fractional solutions.
If you add a cut that removes an integer solution (even one that is not optimal), the solver may return an incorrect solution.
Heuristic solution¶
You may want to add a heuristic of your own if you have some special insight into the problem structure that the solver is not aware of, for example, you can consistently take fractional solutions and intelligently guess integer solutions from them.
Consider the made-up problem:
\begin{array}{ll} \underset{x\in\mathbf{R}^{d}}{\mbox{minimize}} & c^\top x \\ \mbox{subject to} & Ax \leq b,\\ & x\succeq0,\\ & x\in\{0,1\}^{d}, \end{array}For this problem, suppose from real life information, we know that, if $\sum_{i=1}^{n} x_i \leq 10$, then a very good candidate solution is:
[1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0].
Lets see how to implement this as a heuristic solution.
# data
n = 20
m = 5
A = [-0.25149258982896966 0.525287826731042 -0.6656342865169662 -1.2960398772338568 0.9101252450751471 -0.07298248406603706 -1.9148704340623688 -0.5073995272298952 -1.6558511941286744 2.1006659624182586 -0.502359026079171 -0.1708406495941207 1.4161030569819415 0.33735905844690145 -0.10748103771152817 -1.4416340194991104 -0.9578960880328228 -0.1738984790022571 -1.0517643292393826 -0.8271987403702172; -0.8518984622275042 -1.374417162491773 0.35920232369365845 0.8437691247979793 -0.6281577605465152 0.5921264379488904 -0.12756078132890084 -0.44447204507515287 0.7293549470299907 0.715267254601397 -0.9155882952842251 0.35378971887340743 -0.8043683142766567 0.5324223554306367 0.2088297149344946 -0.5594219995662968 0.5632674521223371 -0.2302672262989066 0.7676987968759004 1.0910836780489503; 1.473815753336459 -0.6525879104965642 0.8519411939583414 -0.05756789248416348 -0.7125581880426727 0.4736057460760701 -2.231011632648033 0.5409490591899032 0.1583459153748212 -1.1509507228336586 1.3994115761547934 0.14111034486559706 -0.15123003344570538 -0.547672888665602 -1.9555427017941476 -1.8533179907378834 0.13798098584535193 0.2337797562353011 -0.8404137158789987 0.060446173222487264; 0.6396537082966063 0.856847789735652 1.4805326346158039 0.012324563610194187 1.3977381658753554 1.3342059688961259 -0.4784014905808825 -0.14890693050929457 0.8155899237370289 -0.5697405099766946 1.3446291535605297 0.6840341944716634 1.2484251582871324 1.2891201777341281 -0.2791170028219365 0.43803145770984425 0.4677466100676112 1.3639772554672074 0.8359137382225728 0.8723882764319004; 0.40517145458826054 1.169967487661965 1.7941045258417871 1.035188318563306 1.118495812473751 -0.04027314052794962 0.5438620238342292 -0.8181792084120169 0.08209406151847103 0.6469386439823567 -0.9467882212470308 -0.2866858366079981 0.8836746919594078 -2.0164799655225094 -0.42541330025958685 -0.09145359012880407 0.8920741578367347 -0.5093214870138416 -0.23118339134915017 -1.262095251923206]
c = [-5.724274247670441; 0.872180569098502; -13.289441619771337; -1.284190729811427; -10.090248808669005; 19.226305603166242; -14.323991615118594; -5.8893709748795615; -9.801477473401599; -2.533420139004128; -4.017671140375999; -12.25747413009963; -6.5234635509559205; -18.204822439044932; 10.759517257360242; -2.678837137470244; 2.6260424150728934; -9.929728378562064; -1.08448828496412; -14.883711771646961]
b = [-7.3620594939851545; 1.2864238748369008; -5.191670678971517; 3.4603990262005064; -0.9930993374575348]
5-element Vector{Float64}:
-7.3620594939851545
1.2864238748369008
-5.191670678971517
3.4603990262005064
-0.9930993374575348
# a proper code is as follows:
hrstc_model = Model(Gurobi.Optimizer)
set_optimizer_attribute(hrstc_model, "Presolve", 0)
set_optimizer_attribute(hrstc_model, "Heuristics", 0)
@variable(hrstc_model, x[1:n], Bin)
for i in 1:m
@constraint(hrstc_model, sum(A[i,j]*x[j] for j in 1:n) <= b[i])
end
@objective(hrstc_model, Min, sum(c[i] * x[i] for i in 1:n))
# lazy constraint is added through the following callback function
function my_heuristic_callback_function(cb_data)
# load the current values of the variables at a node of the branch-and-bound tree
x_val = callback_value.(cb_data, x)
if sum(x_val) <= 10 # this is the condition for applying the heuristic
println("[🐼 ] Heuristic condition satisfied")
println("[🐯 ] Status of the callback node is: $(callback_node_status(cb_data,hrstc_model))")
# show the status of the callback node
println("[🐰 ]The values of the variables at the callback node $(x_val)")
# Load the heuristic solution values in a vertical vector pointwise
heuristic_values = vcat(1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0)
# Submit the heuristic solution for potentially improving the current solution
status = MOI.submit(
hrstc_model, MOI.HeuristicSolution(cb_data), x, heuristic_values
)
println("[🙀 ] Status of the submitted heuristic solution is: ", status) # The status shows if the submitted heuristic solution is accepted or not
end
end
# IMPORTANT: 💀 This enables the heuristic
MOI.set(hrstc_model, MOI.HeuristicCallback(), my_heuristic_callback_function)
optimize!(hrstc_model)
Set parameter TokenServer to value "flexlm"
Set parameter Presolve to value 0
Set parameter Heuristics to value 0
Set parameter Heuristics to value 0
Set parameter Presolve to value 0
Gurobi Optimizer version 9.5.0 build v9.5.0rc5 (linux64)
Thread count: 48 physical cores, 96 logical processors, using up to 32 threads
Optimize a model with 5 rows, 20 columns and 100 nonzeros
Model fingerprint: 0xb04b5cd0
Variable types: 0 continuous, 20 integer (20 binary)
Coefficient statistics:
Matrix range [1e-02, 2e+00]
Objective range [9e-01, 2e+01]
Bounds range [0e+00, 0e+00]
RHS range [1e+00, 7e+00]
Variable types: 0 continuous, 20 integer (20 binary)
Root relaxation: objective -6.474229e+01, 9 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 -64.74229 0 4 - -64.74229 - - 0s
[🐼 ] Heuristic condition satisfied
[🐯 ] Status of the callback node is: CALLBACK_NODE_STATUS_FRACTIONAL
[🐰 ]The values of the variables at the callback node [0.14765863276757993, 0.687383649659036, -0.0, 1.0, -0.0, -0.0, 1.0, 1.0, 1.0, -0.0, -0.0, 1.0, -0.0, 0.6051062159183456, 0.7099143090598492, 1.0, -0.0, -0.0, -0.0, 1.0]
[🙀 ] Status of the submitted heuristic solution is: HEURISTIC_SOLUTION_ACCEPTED
H 0 0 -48.2319356 -59.68164 23.7% - 0s
0 0 -49.20427 0 5 -48.23194 -49.20427 2.02% - 0s
Cutting planes:
Gomory: 6
Cover: 3
MIR: 2
RLT: 1
Explored 1 nodes (18 simplex iterations) in 0.03 seconds (0.00 work units)
Thread count was 32 (of 96 available processors)
Solution count 1: -48.2319
No other solutions better than -48.2319
Optimal solution found (tolerance 1.00e-04)
Best objective -4.823193564500e+01, best bound -4.823193564500e+01, gap 0.0000%
User-callback calls 48, time in user-callback 0.03 sec
A good resource to understand the cuts is here.
x_hrstc_opt = value.(x)
20-element Vector{Float64}:
1.0
-0.0
-0.0
1.0
-0.0
-0.0
1.0
1.0
1.0
-0.0
-0.0
-0.0
-0.0
1.0
1.0
1.0
-0.0
-0.0
1.0
-0.0
println(x_hrstc_opt)
[1.0, -0.0, -0.0, 1.0, -0.0, -0.0, 1.0, 1.0, 1.0, -0.0, -0.0, -0.0, -0.0, 1.0, 1.0, 1.0, -0.0, -0.0, 1.0, -0.0]
Warm-starting¶
- Warm-starting: If you know a good feasible solution for your problem, then you can provide
Gurobiwith that solution viawarm-starting.
Consider the same problem as before:
\begin{array}{ll} \underset{x\in\mathbf{R}^{d}}{\mbox{minimize}} & c^\top x \\ \mbox{subject to} & Ax \leq b,\\ & x\succeq0,\\ & x\in\{0,1\}^{d}, \end{array}But rather than custom heuristic, we want to feed the candidate solution is as a warm-start point, so Gurobi will start from this point and explore the tree from there.
x_warm_start = [1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0].
# a proper code is as follows:
x_warm_start = [1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 1.0, 1.0, 0.0, 0.0, 1.0, 0.0];
ws_model = Model(Gurobi.Optimizer)
set_optimizer_attribute(ws_model, "Presolve", 0)
set_optimizer_attribute(ws_model, "Heuristics", 0)
@variable(ws_model, x2[1:n], Bin)
for i in 1:m
@constraint(ws_model, sum(A[i,j]*x2[j] for j in 1:n) <= b[i])
end
# warm-starting here:
set_start_value.(x2, x_warm_start)
@objective(ws_model, Min, sum(c[i] * x2[i] for i in 1:n))
optimize!(ws_model)
Set parameter TokenServer to value "flexlm"
Set parameter Presolve to value 0
Set parameter Heuristics to value 0
Set parameter Heuristics to value 0
Set parameter Presolve to value 0
Gurobi Optimizer version 9.5.0 build v9.5.0rc5 (linux64)
Thread count: 48 physical cores, 96 logical processors, using up to 32 threads
Optimize a model with 5 rows, 20 columns and 100 nonzeros
Model fingerprint: 0x7cfd95e8
Variable types: 0 continuous, 20 integer (20 binary)
Coefficient statistics:
Matrix range [1e-02, 2e+00]
Objective range [9e-01, 2e+01]
Bounds range [0e+00, 0e+00]
RHS range [1e+00, 7e+00]
Loaded user MIP start with objective -48.2319
Variable types: 0 continuous, 20 integer (20 binary)
Root relaxation: objective -6.474229e+01, 9 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 -64.74229 0 4 -48.23194 -64.74229 34.2% - 0s
0 0 -48.23194 0 6 -48.23194 -48.23194 0.00% - 0s
Cutting planes:
Gomory: 3
Cover: 1
MIR: 1
RLT: 3
Explored 1 nodes (17 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 32 (of 96 available processors)
Solution count 1: -48.2319
No other solutions better than -48.2319
Optimal solution found (tolerance 1.00e-04)
Best objective -4.823193564500e+01, best bound -4.823193564500e+01, gap 0.0000%
User-callback calls 49, time in user-callback 0.00 sec
x_ws_opt = value.(x)
20-element Vector{Float64}:
1.0
-0.0
-0.0
1.0
-0.0
-0.0
1.0
1.0
1.0
-0.0
-0.0
-0.0
-0.0
1.0
1.0
1.0
-0.0
-0.0
1.0
-0.0
As an illustrative example, we will consider the sparse regression problem. The sparse regression is a nonconvex optimization problem with applications to gene expression analysis and signal processing etc.
Sparse regression problem. The sparse regression problem is concerned with approximating a vector $b\in\mathbf{R}^{m}$ with a linear combination of at most $k$ columns of a matrix $A\in\mathbf{R}^{m\times n}$ with bounded coefficients. The problem can be written as the following optimization problem
$$
\begin{array}{ll} \textrm{minimize} & \|Ax-b\|^{2}\\ \textrm{subject to} & \mathbf{card}(x)\leq k\\ & \|x\|_{\infty}\leq M, \end{array}
$$
where $x\in\mathbf{R}^{n}$ is the decision variable, and $A\in\mathbf{R}^{m\times n},b\in\mathbf{R}^{m},$ and $M\in\mathbf{R}$ are problem data. Here, $\mathbf{card}(x)$ is the number of nonzero components in $x$.
Modeling sparse regression problem as a MIQP. The sparse regression problem can be modeled as the following MIQP: $$ \begin{array}{ll} \textrm{minimize} & \|Ax-b\|^{2}\\ \textrm{subject to} & |x_{i}|\leq My_{i},\quad i=1,\ldots,n \qquad (1)\\ & \sum_{i=1}^{n}y_{i}\leq k\\ & x\in\mathbf{R}^{n},y\in\{0,1\}^{n}, \end{array} $$ where $x, y$ are decision variables.
We can write our objective function as $$ \begin{align*} \|Ax-b\|^{2} & =(Ax-b)^{\intercal}(Ax-b)\\ & =(x^{\intercal}A^{\intercal}-b^{\intercal})(Ax-b)\\ & =x^{\intercal}(A^{\intercal}A)x+(-2A^{\intercal}b)^{\intercal}x+\|b\|^{2}, \end{align*} $$ which takes the function in a quadratic form.
Rewriting the objective in a compatible format. If we define $S=A^{\intercal}A,$ $c=-2A^{\intercal}b,$ and $d=\|b\|^{2},$ then we can write the objective function as: $$ \sum_{i=1}^{n}\sum_{j=1}^{n}S_{ij}x_{i}x_{j}+\sum_{i=1}^{n}c_{i}x_{i}+d, $$ which is more compatible as an input for JuMP.
Rewriting the bound constraint in a more compatible format. Also, for JuMP, we write the bound constraint $|x_{i}|\leq My_{i}$ as two constraints: $x_i \leq M y_i$, and $-M y_i \leq x_i$ for $i=1,\ldots,n$.
# Data, change it accordingly
# ---------------------------
m = 5
n = 10
A = randn(m,n)
b = randn(m)
M = 1
k = convert(Int64, round(m/3))
# Renaming a bunch of variables
S = A'*A
c = -2*A'*b
d = norm(b)^2
5.652765754068141
# Define the model
# ----------------
model = Model(with_optimizer(Gurobi.Optimizer)) # define name of the model, it could be anything, not necessarily "model"
# Variables
# ---------
@variable(model, x[1:n]) # define variable x
@variable(model, y[1:n], Bin) # define the binary variable y
# Objective
# ---------
sense = MOI.MIN_SENSE # by this command, we are programatically defining a quadratic objective to be minimized
@objective(model, sense, sum(S[i,j]*x[i]*x[j] for i in 1:n, j in 1:n)+ sum(c[i]*x[i] for i in 1:n) + d) # define the objective
# Constraints
# ------------
@constraint(model, con_lb[i=1:n], -M*y[i] <= x[i]) # lower bound constraint
@constraint(model, con_ub[i=1:n], x[i] <= M*y[i]) # upper bound constraint
@constraint(model, con_bd_sum, sum(y[i] for i in 1:n) <= k) # cardinality constraint in terms of y
# Run the optimizer
# -----------------
status=optimize!(model) # time to optimize!
Set parameter TokenServer to value "flexlm"
Gurobi Optimizer version 9.5.0 build v9.5.0rc5 (linux64)
Thread count: 48 physical cores, 96 logical processors, using up to 32 threads
Optimize a model with 21 rows, 20 columns and 50 nonzeros
Model fingerprint: 0x4ad08fc0
Model has 55 quadratic objective terms
Variable types: 10 continuous, 10 integer (10 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [1e+00, 7e+00]
QObjective range [1e-01, 3e+01]
Bounds range [0e+00, 0e+00]
RHS range [2e+00, 2e+00]
Found heuristic solution: objective 5.6527658
Presolve time: 0.00s
Presolved: 21 rows, 20 columns, 50 nonzeros
Presolved model has 55 quadratic objective terms
Variable types: 10 continuous, 10 integer (10 binary)
Root relaxation: objective 1.111026e-01, 65 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 0.11110 0 4 5.65277 0.11110 98.0% - 0s
H 0 0 0.4923181 0.11110 77.4% - 0s
0 0 0.33538 0 4 0.49232 0.33538 31.9% - 0s
0 0 0.33538 0 4 0.49232 0.33538 31.9% - 0s
0 0 0.37953 0 2 0.49232 0.37953 22.9% - 0s
0 0 0.37953 0 2 0.49232 0.37953 22.9% - 0s
0 0 0.37953 0 1 0.49232 0.37953 22.9% - 0s
Explored 1 nodes (99 simplex iterations) in 0.01 seconds (0.00 work units)
Thread count was 32 (of 96 available processors)
Solution count 3: 0.492318 5.65277 5.65277
Optimal solution found (tolerance 1.00e-04)
Best objective 4.923181247866e-01, best bound 4.923181247866e-01, gap 0.0000%
User-callback calls 193, time in user-callback 0.00 sec