How to create NumPy arrays from scratch?¶
This tutorial is all about understanding the NumPy python package and creating NumPy arrays from scratch.¶

Regardless of the data, the first step in analyzing them is transforming them into an array of numbers. The fundamental process of doing data science is efficiently is storing and manipulating numerical arrays. Because of this Python has specialized tools for handling numerical arrays:
- NumPy Package
- Pandas Package
This tutorial only focuses on the NumPy package. However, Pandas package documentation will be provided in the latter days. Let's get started.
What is NumPy?¶
NumPy stands for *Numerical Python*. NumPy provides an efficient way to store and operate on dense data buffers. With the help of the NumPy library, we can create and operate with arrays to store the data. In some ways, NumPy’s arrays are like Python’s list built-in function.
How to execute NumPy and check its version?¶
Let’s get started. You can execute the below programs in your favorite python editors like PyCharm, Sublime Text, or Notebooks like Jupyter and Google Colab. It's basically your preference to choose an IDE of your choice. I am using Google Colab to write my code because it gives me tons of options to provides good documentation. Also, visit the NumPy website to get more guidelines about the installation process.
Once you have installed the NumPy on your IDE you need to import it. It’s often a good practice to check the version of the library. So to install the NumPy library you need to use the below code.
import numpy
print(numpy.__version__)
1.18.1
Just make sure that you the latest NumPy version to use all the features and options. Rather than using *“numpy”* we can use an alias as *“np”. This is called “Aliasing”. Now the point of using an alias is we can use “np”* rather *“numpy”* which is long to type every time when we use its methods. So creating an alias and checking the version can be done as shown below:
import numpy as np
print(np.__version__)
1.18.1
From now on we can use “np” rather than “numpy” every time.
Why Numpy arrays came into the picture when there were python’s fixed type arrays?¶
Python provides several different options for storing efficient, fixed-type data. Python has a built-in array module called “array” which is used to create arrays of uniform type. This was its main disadvantage.
import array
# Creating an array
print(array.array('i', [1, 2, 3, 4, 5]))
array('i', [1, 2, 3, 4, 5])
The *“i”* here indicates the integer data. We cannot try to store other types of data in the array module. It often leads to an error.
import array
# Creating an array
print(array.array('i', [1, 2.0, 3, 4, 5]))
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) <ipython-input-4-c92d6f7f41d6> in <module> 1 import array 2 # Creating an array ----> 3 print(array.array('i', [1, 2.0, 3, 4, 5])) TypeError: integer argument expected, got float
However, Python’s array module provides efficient storage of array-based data. But NumPy arrays can perform efficient operations on that type of data. There are two ways that we can create NumPy arrays:
- Creating a NumPy array from Python Lists
- Creating a NumPy array from scratch
import numpy as np
# Creating a list named "a"
a = [1, 2, 3, 4, 5]
print(type(a))
<class 'list'>
# Creating a numpy array from the list
print(np.array(a))
[1 2 3 4 5]
print(type(np.array(a)))
<class 'numpy.ndarray'>
The NumPy library is limited to arrays with the same type, if there is a type mismatch then it would upcast if possible. Consider the below example:
import numpy as np
# Creating a list named "a"
a = [1, 2.0, 3, 4, 5]
print(type(a))
<class 'list'>
# Creating a numpy array from the list
print(np.array(a))
[1. 2. 3. 4. 5.]
print(type(np.array(a)))
<class 'numpy.ndarray'>
So the original list was integers with one floating value but the numpy array upcasted it to all *floating-point* numbers. The integers are upcasted to floating-point numbers. Below is a small diagram that gives you enough knowledge to understand the upcast and downcast.
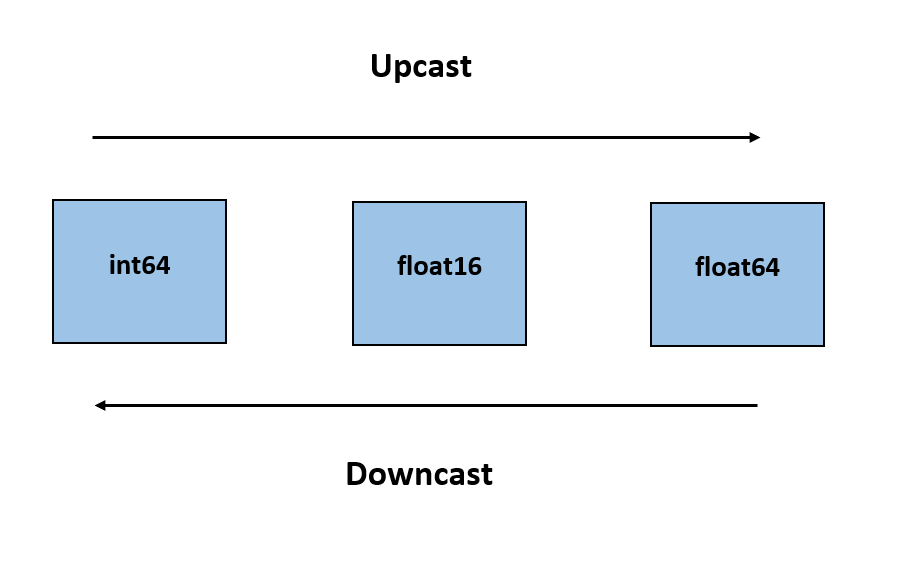
Also explicitly setting the data type is also possible. This can be done using the keyword *“dtype”*.
import numpy as np
# Creating a list named "a"
a = [1, 2, 3, 4, 5]
# Creating a numpy array from the list
np.array(a, dtype='float64')
print(np.array(a, dtype='float64'))
[1. 2. 3. 4. 5.]
As seen from the above example, the integer type list data is converted into the float type data by using the *“dtype”* keyword. Numpy arrays can also be *multidimensional* (Array within an array). Here’s one way of doing it.
import numpy as np
# Creating a list named "a"
a = [1, 2, 3, 4, 5]
# Creating a numpy array from the list
np.array([range(i, i + 4) for i in a])
array([[1, 2, 3, 4],
[2, 3, 4, 5],
[3, 4, 5, 6],
[4, 5, 6, 7],
[5, 6, 7, 8]])
Hint: Just increment the “i” value in terms of 1 (i+1, 2, 3, 4, …) by doing so you can increase the dimension of the array too. The above array is treated as 2D — Array.
Creating a NumPy array from scratch¶
Numpy arrays are actually used for creating larger arrays. It is more efficient to create large arrays from scratch using the numpy package library. Below are some of the examples of creating numpy arrays from scratch.
Creating an array filled with zeros of length 5¶
We can do this using the numpy built-in method called zeros as shown below:
import numpy as np
# Creating a numpy array of zeros of length 5
print(np.zeros(5, dtype='int'))
[0 0 0 0 0]
There are some standard numpy data types available. I cannot just discuss all of them in one stretch. Most of them are never used. So I will be providing the data types of numpy array in the form of a chart below just use that accordingly. If you don't know how to use the datatypes refer to Explicitly changing the array datatypes above its → *dtypes = “name of the datatype”*
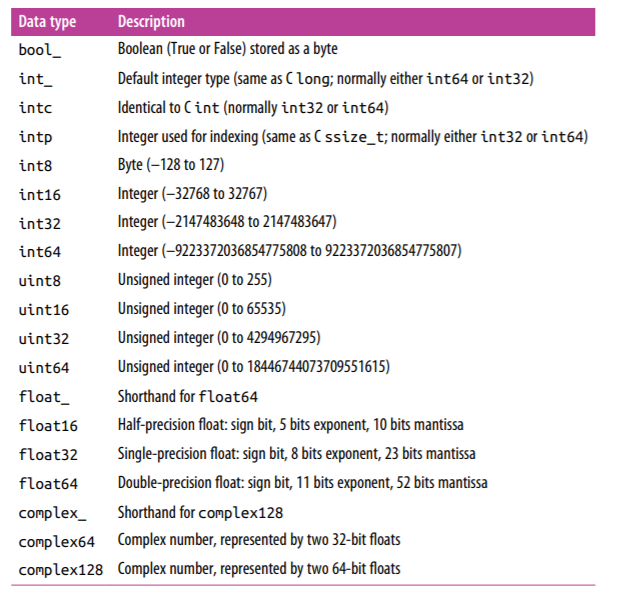
Creating a 3 x 4 array filled with 1's¶
Thanks to NumPy because we don’t have to put the array inside a looping statement (I hate to do that ;)). All you have to do is just mention the rows and the columns that you want your array to have inside the numpy.one method.
import numpy as np
# Creating a numpy array of 1’s which should have 3 rows and 4 columns
print(np.ones((3, 4)))
[[1. 1. 1. 1.] [1. 1. 1. 1.] [1. 1. 1. 1.]]
So the number 3 → rows and 4 → obviously columns.
Filling the numpy arrays with a particular number¶
Till now we have seen filling the array with 0’s and 1’s but we should also know that numpy allows us to fill the arrays with any specific number of our choice. We can do this with the help of *numpy.full* method. For example, let us fill the array with the number 500.
import numpy as np
# Creating a numpy array of 500’s which should have 3 rows and 4 columns
print(np.full((3, 4), 500))
[[500 500 500 500] [500 500 500 500] [500 500 500 500]]
With the help of the full method, we can add any number of our choice to our array.
Creating a numpy array of random numbers¶
*Uniform distribution →* It is a probability distribution in which all the outcomes are equally likely. For example, tossing a coin has the probability of uniform distribution because the outcomes are a most likely head or a tail. It’s never going to be both at the same time. The NumPy package library provides us a uniform distribution method to generate random numbers called *numpy.random.uniform*.
import numpy as np
# Create a 3x3 array of uniformly distributed
# random values between 0 and 1
print(np.random.random((3, 3)))
[[0.43391692 0.91483616 0.37762892] [0.10061519 0.8151521 0.12661754] [0.80940409 0.85737543 0.43698751]]
Also, the numpy package library has a seed generator along with the random number generator, with the help of the seed method we can control the sequence of the random numbers being generated. Most of them don’t know the specialty of the seed method and its purpose. To know more about the seed method refer below.
Why do we need “seed” inside the random number generator?¶
If we use the seed every time then we get the same sequence of random numbers.
So, the same seed yields the same sequence of random numbers.
import numpy as np
# Create a random number arrays of size 5
np.random.seed(0)
print(np.random.random(5))
[0.5488135 0.71518937 0.60276338 0.54488318 0.4236548 ]
No matter how many times you execute the above code you get the same random numbers every time. To know the difference just comment on the code (#) and then see the difference. Let us explore the seed method to a bit more extent. For example, if you use seed(1) and then generate some random numbers they will be the same with the ones you generate later on but with the same seed (1) as shown below.
import numpy as np
# Create a random number arrays of size 5
np.random.seed(1)
print(np.random.random(5))
[4.17022005e-01 7.20324493e-01 1.14374817e-04 3.02332573e-01 1.46755891e-01]
print(np.random.random(5))
[0.09233859 0.18626021 0.34556073 0.39676747 0.53881673]
np.random.seed(1)
print(np.random.random(5))
[4.17022005e-01 7.20324493e-01 1.14374817e-04 3.02332573e-01 1.46755891e-01]
*Same seed same random numbers ensure “Reproducibility”* — Quora.com
Also, the range of the seed is from 0 and 2**32–1. Don’t just use negative numbers as the seed value, if you do so you will get an error as shown below:
import numpy as np
np.random.seed(-1)
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-21-8b72c1b875d1> in <module> 1 import numpy as np ----> 2 np.random.seed(-1) mtrand.pyx in numpy.random.mtrand.RandomState.seed() _mt19937.pyx in numpy.random._mt19937.MT19937._legacy_seeding() _mt19937.pyx in numpy.random._mt19937.MT19937._legacy_seeding() ValueError: Seed must be between 0 and 2**32 - 1
*Normal Distribution →* Is Also known as the Gaussian Distribution, a continuous probability distribution for a real-valued random variable. It is also known as a *symmetric distribution* where most of the values cluster at the center of the peak. The standard deviation determines the spread.
The NumPy package library provides us a uniform distribution method to generate random numbers called *numpy.random.normal. The syntax is almost the same as the uniform distribution but you need to add two more vital data here known as the mean* and the *standard deviation*.
import numpy as np
# Create a 3x3 array of normally distributed random values
# with mean 0 and standard deviation 1
print(np.random.normal(0, 1, (3, 3)))
[[-1.10593508 -1.65451545 -2.3634686 ] [ 1.13534535 -1.01701414 0.63736181] [-0.85990661 1.77260763 -1.11036305]]
Creating an identity matrix using numpy array¶
An identity matrix is a matrix where the principal diagonal elements are 1 and the other elements except the principal diagonal elements are 0. The numpy package library provides a method to generate an identity matrix called the eye. An identity matrix is a square matrix meaning it has equal rows and columns.
import numpy as np
# Create a identity matrix of 4 rows and 4 columns
print(np.eye(4))
[[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 1.]]
The number 4 represents the rows and columns since it is a square matrix we only need to specify the value once (4 in this case).
This is the end of this tutorial “How to create NumPy arrays from scratch?”, this is just the introductory tutorial for NumPy Package library. However, much more complex concepts of the NumPy package library will be discussed in the upcoming tutorials. Thank you guys for spending your time reading my tutorial. I hope you enjoyed it. If you have any doubts related to NumPy, then the comment section is all yours. Until then Goodbye, See you have a good day.
Important Numpy mathematical functions¶
python numpy libary provides several important mathematical functions such as dot product,Multiplication,Broadcasting,mean,standard deviation,min,max and transpose of nd array.
Multiplication¶
Function of scalar mutiplication is to multiply consective elements of nd array
u=np.array([1,2,3])
v=np.array([4,5,6])
print(u*v)
[ 4 10 18]
Dot Product¶
dot_product=np.dot(u,v)
print(dot_product)
32
Broadcasting¶
Term broadcasting stands for situation when we add a certain number to entire matrix.
u_broadcasted=u+1
Mininum and maximum¶
minimum_element_of_u=u.min()
maximum_element_of_u=u.max()
print(minimum_element_of_u,maximum_element_of_u)
1 3
Mean¶
print("mean of matrix u is ",u.mean())
mean of matrix u is 2.0
Standard deviation.¶
print("standard deviation of matrix u is ",u.std())
standard deviation of matrix u is 0.816496580927726