Table of Contents¶

Ce notebook Jupyter, utilisant OCaml (via le kernel Ocaml), est une correction non officielle d'un texte de modélisation pour l'option informatique de l'agrégation externe de mathématiques.

Il s'agit du texte public2012-D5.

Cette tentative de correction partielle a été rédigée par Lilian Besson (sur GitHub ?, sur Bitbucket ?), et est open-source.

J'avais déjà rédigé une solution, pendant ma propre préparation à l'agrégation en 2013/2014, voir ce fichier.

Retour ?

Vous avez trouvé un bug ? → Signalez-le moi svp !, merci d'avance.

Vous avez une question ? → Posez la svp !

Proposition d'implémentation, en OCaml ¶

Pour l'option informatique (D) de l'agrégation de mathématiques (en France).¶

Attention : ce document ne prétend pas être LA correction du texte, mais un exemple de solution.

Je me suis inspiré des propositions d'implémentations rédigées par les élèves qui ont préparé ce texte en 3h50 le lundi 13 mai 2019.

Exercice requis¶

L'exercice de programmation était en page 2/8 du texte, après l'explication du problème et de l'algorithme de Bresenham.

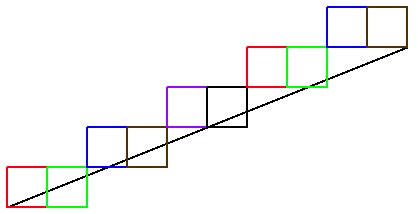
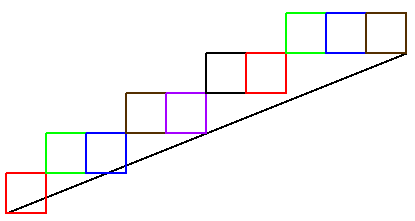
Écrire un programme permettant de représenter le segment $[A B]$, où $A= (a_1,a_2)$ et $B=(b_1,b_2)$, en suivant l'algorithme de Bresenham. On supposera que $a_1<b_1$, $a_2 \leq b_2$ et que la pente $\alpha$ de la droite est inférieure à $1$. La sortie du programme sera la liste des couples $(x_i,y_i)$ des points représentant le segment.

Attention, on rappelle que le rapport du jury précise explicitement que dans les exercices de programmation liste de … signifie liste OU tableau, au choix du candidat ou de la candidate.

Choix de structure de données¶

Soit $n = b_1 - a_1 \in\mathbb{N}$. Ici, on connaît à l'avance le nombre de points que doit contenir la solution, donc utiliser un tableau de $n+1$ points est une bonne idée.

En OCaml¶

On va préférer :

let segment = Array.make (n+1) (a1, a2) in
...

for i = 1 to n do
    let xi, yi = ..., ... in
    segment.(i) <- (xi, yi);
done

à :

let segment = ref [(a1, a2)] in
...

for i = 1 to n do
    let xi, yi = ..., ... in
    segment := (xi, yi) :: !segment;
done

En Python¶

On pourrait de même créer un tableau dès le début. On va préférer :

segment = [ (0,0) for i in range(n+1) ]
segment = [ (0,0) ] * (n+1)
...
for i in range(n):
    xi, yi = ..., ...
    segment[i] = (xi, yi)

à :

segment = [ (a1, a2) ]
...
for i in range(n):
    xi, yi = ..., ...
    segment.append(xi, yi)

Réponse¶

On utilise un type point pour représenter les points de coordonées entières $(x, y) \in\mathbb{Z}^2$, cela facilitera l'affichage des signatures :

In [3]:

type point = (int * int);;

let point_a : point = (0, 0)
and point_b : point = (4, 3);;

Out[3]:

type point = int * int

Out[3]:

val point_a : point = (0, 0)
val point_b : point = (4, 3)

In [5]:

type segment = point array;;

Out[5]:

type segment = point array

La fonction suivante renvoie un tableau de $n+1$ points, représentant le segment $[a, b]$ obtenus avec l'algorithme de Bresenham.

Complexité temporelle : $\mathcal{O}(n)$
Complexité mémoire : $\mathcal{O}(n)$, où n = b1 - a1. (dans tous les cas)

In [50]:

let bresenham (a : point) (b : point) : segment =
  let a1, a2 = a
  and b1, b2 = b in
  let n = b1 - a1 in
  let segment_ab = Array.make (n+1) a in
  let alpha_normalisee = b2 - a2 in (* pente normalisée, ie alpha*n dans *)
  let erreur = ref 0 in
  let y_tilde = ref a2 in
  for i = 1 to n-1 do
    if 2 * (!erreur + alpha_normalisee) <= n then
      erreur := !erreur + alpha_normalisee
    else begin
      erreur := !erreur + alpha_normalisee - n;
      y_tilde := !y_tilde + 1;
    end;
    segment_ab.(i) <- (a1 + i, !y_tilde);
  done;
  segment_ab.(n) <- b;
  segment_ab
;;

Out[50]:

val bresenham : point -> point -> segment = <fun>

On fait quelques exemples...¶

In [51]:

bresenham (0, 0) (5, 2);;

Out[51]:

- : segment = [|(0, 0); (1, 0); (2, 1); (3, 1); (4, 2); (5, 2)|]

In [52]:

bresenham (0, 0) (5, 5);;

Out[52]:

- : segment = [|(0, 0); (1, 1); (2, 2); (3, 3); (4, 4); (5, 5)|]

Si une hypothèse n'est pas vérifié¶

On vérifie que l'ordre des arguments est important, le programme exige que $a_1 < b_1$ et $a_2 \leq b_2$ :

In [53]:

bresenham (0, 0) (-5, 2);;

Exception: Invalid_argument "Array.make".
Raised by primitive operation at file "[50]", line 6, characters 2-430
Called from file "toplevel/toploop.ml", line 180, characters 17-56

Si la pente est $\alpha>1$, le programme ne fait pas ce qu'on espérait, car ses hypothèses ne sont pas respectées :

In [54]:

bresenham (0, 0) (0, 2);;

Out[54]:

- : segment = [|(0, 2)|]

Bonus : deux autres méthodes (droites inférieure et supérieure)¶

Ce n'est pas exigé dans le texte, mais on pouvait facilement implémenter la méthode qui longe la droite au plus près inférieurement, et au plus près supérieurement.

Pour la première, c'est assez facile et on peut aussi travailler uniquement avec des entiers :
- Complexité temporelle : $\mathcal{O}(n)$
- Complexité mémoire : $\mathcal{O}(n)$, où n = b1 - a1. (dans tous les cas)

In [55]:

let au_plus_pres_inferieurement (a : point) (b : point) : segment =
  let a1, a2 = a
  and b1, b2 = b in
  let n = b1 - a1 in
  let segment_ab = Array.make (n+1) a in
  let alpha_normalisee = b2 - a2 in (* pente normalisée, ie alpha*n dans *)
  for i = 1 to n-1 do
    (* on laisse la division entière faire la partie inférieure *)
    segment_ab.(i) <- (a1 + i, (alpha_normalisee * i + a2 * (b1-a1)) / (b1 -a1));
  done;
  segment_ab.(n) <- b;
  segment_ab
;;

Out[55]:

val au_plus_pres_inferieurement : point -> point -> segment = <fun>

Sur les mêmes exemples, on voit la différence, quand la pente est $\alpha<1$ :

In [56]:

bresenham (0, 0) (5, 2);;
au_plus_pres_inferieurement (0, 0) (5, 2);;

Out[56]:

- : segment = [|(0, 0); (1, 0); (2, 1); (3, 1); (4, 2); (5, 2)|]

Out[56]:

- : segment = [|(0, 0); (1, 0); (2, 0); (3, 1); (4, 1); (5, 2)|]

In [57]:

bresenham (0, 0) (5, 5);;
au_plus_pres_inferieurement (0, 0) (5, 5);;

Out[57]:

- : segment = [|(0, 0); (1, 1); (2, 2); (3, 3); (4, 4); (5, 5)|]

Out[57]:

- : segment = [|(0, 0); (1, 1); (2, 2); (3, 3); (4, 4); (5, 5)|]

Pour la droite au plus près supérieurement, on va illustrer l'utilisation d'arithmétique flottante et de la fonction ceil
- Complexité temporelle : $\mathcal{O}(n)$
- Complexité mémoire : $\mathcal{O}(n)$, où n = b1 - a1. (dans tous les cas)

In [58]:

ceil;;

Out[58]:

- : float -> float = <fun>

In [59]:

let ceil_to_int x = int_of_float (ceil x);;

Out[59]:

val ceil_to_int : float -> int = <fun>

In [60]:

let au_plus_pres_superieurement (a : point) (b : point) : segment =
  let a1, a2 = a
  and b1, b2 = b in
  let n = b1 - a1 in
  let segment_ab = Array.make (n+1) a in
  let alpha = (float_of_int (b2 - a2)) /. (float_of_int n) in (* pente normalisée, ie alpha*n dans *)
  for i = 1 to n-1 do
    segment_ab.(i) <- (a1 + i, ceil_to_int ((float_of_int a2) +. alpha *. (float_of_int i)));
  done;
  segment_ab.(n) <- b;
  segment_ab
;;

Out[60]:

val au_plus_pres_superieurement : point -> point -> segment = <fun>

Sur les mêmes exemples, on voit la différence, quand la pente est $\alpha<1$ :

In [61]:

bresenham (0, 0) (5, 2);;
au_plus_pres_superieurement (0, 0) (5, 2);;

Out[61]:

- : segment = [|(0, 0); (1, 0); (2, 1); (3, 1); (4, 2); (5, 2)|]

Out[61]:

- : segment = [|(0, 0); (1, 1); (2, 1); (3, 2); (4, 2); (5, 2)|]

In [62]:

bresenham (0, 0) (5, 5);;
au_plus_pres_superieurement (0, 0) (5, 5);;

Out[62]:

- : segment = [|(0, 0); (1, 1); (2, 2); (3, 3); (4, 4); (5, 5)|]

Out[62]:

- : segment = [|(0, 0); (1, 1); (2, 2); (3, 3); (4, 4); (5, 5)|]

Illustration¶

En bonus, on montre une illustration (on ferait des dessins au tableau).

Par la sélection de Bresenham¶

Par la sélection inférieure¶

Par la sélection supérieure¶

Autres bonus : calculer le mot binaire codant les déplacements¶

Si on utilise par exemple la droite longeant au plus près inférieurement, la fonction suivante renvoie la suite des déplacements horizontaux ou diagonaux pour longer le segment $[a, b]$.

In [63]:

type mot_binaire = bool array;;

Out[63]:

type mot_binaire = bool array

In [69]:

let deplacements (a : point) (b : point) : mot_binaire =
  let a1, a2 = a
  and b1, b2 = b in
  let n = b1 - a1 in
  let mot_binaire_ab : mot_binaire = Array.make n false in
  let alpha_normalisee = b2 - a2 in (* pente normalisée, ie alpha*n dans *)
  let y0 = ref 0 and y1 = ref 0 in
  for i = 1 to n do
    y0 := !y1;
    (* on laisse la division entière faire la partie inférieure *)
    y1 := (alpha_normalisee * i + a2 * (b1-a1)) / (b1 -a1);
    mot_binaire_ab.(i-1) <- !y0 != !y1;
  done;
  mot_binaire_ab
;;

Out[69]:

val deplacements : point -> point -> mot_binaire = <fun>

Sur les mêmes exemples, on voit la différence, quand la pente est $\alpha<1$ :

In [70]:

au_plus_pres_inferieurement (0, 0) (5, 2);;
deplacements (0, 0) (5, 2);;

Out[70]:

- : segment = [|(0, 0); (1, 0); (2, 0); (3, 1); (4, 1); (5, 2)|]

Out[70]:

- : mot_binaire = [|false; false; true; false; true|]

Le mot renvoyé est $(0 0 1 0 1)$, comme prévu.

Et si la pente est $\alpha=1$, le mot sera $(11111)$.

In [71]:

au_plus_pres_inferieurement (0, 0) (5, 5);;
deplacements (0, 0) (5, 5);;

Out[71]:

- : segment = [|(0, 0); (1, 1); (2, 2); (3, 3); (4, 4); (5, 5)|]

Out[71]:

- : mot_binaire = [|true; true; true; true; true|]

Conclusion¶

Attention¶

Les 35/40 minutes de passage au tableau ne doivent PAS être uniquement consacrée à la présentation de vos expériences sur l'ordinateur !

Il faut aussi :

faire une introduction générale (citer des mots clés),
présenter le plan de votre présentation,
introduire les notations, les objectifs et les résultats donnés par le texte,
prouver ou exposer des développements theoriques personnels (à choisir parmi la liste proposée, mais pas seulement),
etc.

C'est tout pour aujourd'hui les amis ! Allez voir d'autres notebooks si vous voulez.

Table of Contents¶

Agrégation externe de mathématiques, texte d’exercice diffusé en 2012¶

Épreuve de modélisation, option informatique¶

Proposition d'implémentation, en OCaml¶

Pour l'option informatique (D) de l'agrégation de mathématiques (en France).¶

Exercice requis¶

Choix de structure de données¶

En OCaml¶

En Python¶

Réponse¶

On fait quelques exemples...¶

Si une hypothèse n'est pas vérifié¶

Bonus : deux autres méthodes (droites inférieure et supérieure)¶

Illustration¶

Par la sélection de Bresenham¶

Par la sélection inférieure¶

Par la sélection supérieure¶

Autres bonus : calculer le mot binaire codant les déplacements¶

Conclusion¶

Attention¶

Proposition d'implémentation, en OCaml ¶