Here we will see another dimesionality reduction technique called LDA and compare it with PCA. Later on, using this we will do topic modelling.
- LDA
- LDA vs PCA
- Topic Modelling
import matplotlib.pyplot as plt
import nltk
import numpy as np
import pandas as pd
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
from nltk.stem.porter import *
from nltk.tokenize import word_tokenize
from sklearn.datasets import fetch_20newsgroups, load_iris
from sklearn.decomposition import PCA, LatentDirichletAllocation
from sklearn.feature_extraction.text import CountVectorizer
LDA(Linear Discriminant Analysis) and LDA vs PCA¶
LDA is a dimesionality reduction tecnique.It transforms your data from say 'n' dimensions to 'k'dimensions. Both are pretty similar in output but with one major difference. LDA is a supervised algorithm whereas PCA is not, PCA ignores class labels.
As, we have seen in previous weeks, PCA tries to find directions of maximum variance. PCA projects data onto new axis in such a way they explain the maximum variance without taking class labels into consideration. LDA on the other hand, creates new axis in such a way that when we project data on this axis, there is a maximum separation bewtween two class categories. LDA tries to separate classes as much as feasible on the new axis.
Below is the demonstration of same with Iris dataset.
data=load_iris().data
target=load_iris().target
target_names=load_iris().target_names
dataframe=pd.DataFrame(data=np.concatenate((data,target.reshape(150,1)),axis=1),columns=['col_1','col_2','col_3','col_4','target'])
dataframe.head()
dataframe.drop(columns=['target'],axis=1,inplace=True)
pca = PCA (n_components=2)
X_feature_reduced = pca.fit(dataframe).transform(dataframe)
plt.scatter(X_feature_reduced[:,0],X_feature_reduced[:,1],c=target)
plt.title("PCA")
plt.show()
lda = LatentDirichletAllocation(n_components=2)
X_feature_reduced = lda.fit(dataframe).transform(dataframe)
plt.scatter(X_feature_reduced[:,0],X_feature_reduced[:,1],c=target)
plt.title('LDA')
plt.show()
Observation¶
As we can see from above that LDA projected data on new axis in such a way that class are separated as much as possible.
How does LDA achieves this?¶
LDA creates new axis based on two criteria:
- Distance between means of classes
- Variation within each category
It projects data on new axis and finds mean for each class and variance for each class. It tries to maximise the distance between class means and tries to minimise the variation with each class. Using these into consideration we get a new axis.
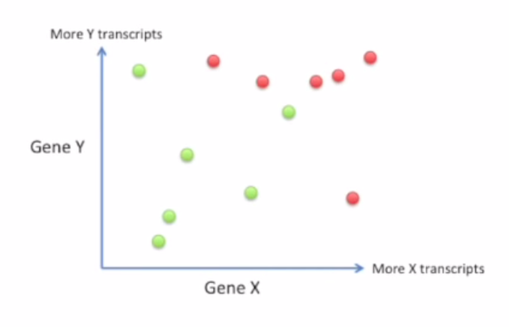 Above is the data for two Genes, we want to project them on new axis with one dimension.
Above is the data for two Genes, we want to project them on new axis with one dimension.

Criterion which we choose above to solve this is
(µ1-µ2)^2 /(s1+s2)^2
,where µ1 and µ2 are mean of each class and 's1 and s2' are variation/scatter within a clas while making new axis. We try to maximise this criteria while making new axis.
Topic modelling¶
Topic modelling is a method of assigning topic to each document. Each topic is made up of certain words.
Consider for example:
We have two topics, topic 1 and topic 2. 'Topic1' is represented by 'apple, banana, mango' and topic2 is represented by 'tennis, cricket, hockey'. We can infer that topic1 is talking about fruits and topic2 is talking about sports. We can assign new incoming document into one of these topics and that can be used for clustering purpose too. It is used in recommendation systems and many more.
Another example: Consider we have 6 documents
- apple banana
- apple orange
- banana orange
- tiger cat
- tiger dog
- cat dog
What topic modelling would do is if want to extract say two topic out of these documents, it will give two distributions, topic-word distribution and doc-topic distribution. In topic-word representation it should give word wise distribution for each topic and in doc-topic it would give for each document, it's topic representation or distribution of document for each topic.
It's ideal topic-word distribution should be:
| Topic | Apple | Banana | Orange | Tiger | Cat | Dog |
|---|---|---|---|---|---|---|
| Topic 1 | .33 | .33 | .33 | 0 | 0 | 0 |
| Topic 2 | 0 | 0 | 0 | 0.33 | 0.33 | 0.33 |
and it's ideal document-topic distrubution should be:
| Topic | doc1 | doc2 | doc3 | doc4 | doc5 | doc6 |
|---|---|---|---|---|---|---|
| Topic 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| Topic 2 | 0 | 0 | 0 | 1 | 1 | 1 |
and now suppose we have a new document say, ' cat dog apple', its topic wise representation should be
Topic1: 0.33
Topic2: 0.63
LDA is highly used for this purpose.It's usage for topic modelling and has been demonstrated below. We give to it the number of topics we want to find out of the corpus. Remember it follow bow approach therefore, relationship between words are lost in this manner.
lemmatizer=WordNetLemmatizer() #For words Lemmatization
stemmer=PorterStemmer() #For stemming words
stop_words=set(stopwords.words('english'))
def TokenizeText(text):
'''
Tokenizes text by removing various stopwords and lemmatizing them
'''
text=re.sub('[^A-Za-z0-9\s]+', '', text)
word_list=word_tokenize(text)
word_list_final=[]
for word in word_list:
if word not in stop_words:
word_list_final.append(lemmatizer.lemmatize(word))
return word_list_final
def gettopicwords(topics,cv,n_words=10):
'''
Print top n_words for each topic.
cv=Countvectorizer
'''
for i,topic in enumerate(topics):
top_words_array=np.array(cv.get_feature_names())[np.argsort(topic)[::-1][:n_words]]
print "For topic {} it's top {} words are ".format(str(i),str(n_words))
combined_sentence=""
for word in top_words_array:
combined_sentence+=word+" "
print combined_sentence
print " "
df=pd.read_csv('million-headlines.zip',usecols=[1])
df.head()
%%time
num_features=100000
# cv=CountVectorizer(min_df=0.01,max_df=0.97,tokenizer=TokenizeText,max_features=num_features)
cv=CountVectorizer(tokenizer=TokenizeText,max_features=num_features)
transformed_data=cv.fit_transform(df['headline_text'])
transformed_data
%%time
no_topics=10 ## We can change this, hyperparameter
lda = LatentDirichletAllocation(n_components=no_topics, max_iter=5, learning_method='online', learning_offset=50.,random_state=0).fit(transformed_data)
Lda.components_ is a topic_word table, it shows representation of each word in the topic. components_[i, j] can be viewed as pseudocount that represents the number of times word j was assigned to topic i. It can also be viewed as distribution over the words for each topic after normalization
gettopicwords(lda.components_,cv)
Assigning new topic¶
We can see that each document is a combination of each topic. Let's see topic represntation of first ten documents.
First ten documents and their topicwise representation is shown below
docs=df['headline_text'][:10]
data=[]
for doc in docs:
data.append(lda.transform(cv.transform([doc])))
cols=['topic'+str(i) for i in range(1,11)]
doc_topic_df=pd.DataFrame(columns=cols,data=np.array(data).reshape((10,10)))
doc_topic_df['major_topic']=doc_topic_df.idxmax(axis=1)
doc_topic_df['raw_doc']=docs
doc_topic_df
We saw how LDA can be used for topic modelling. This can be used for document custering based on the doc topic representation.