jax

JAX Basics¶

What mostly constitutes of Deep Learning at granular level?

Bandwidth: Loading and transfer of data from memory
MatMul Ops: Array manipulation and operations
Non Matmul Ops: Algorithms with support to auto-differentiation

If theoretically deep-learning is all applied-maths, then why scientific computing library like Numpy is not suitable? Or, Why powerful deep learning frameworks like Tensorflow and PyTorch are not built on Numpy?

Numpy cannot run on accelerated hardware.
Numpy doesn't have auto differentiation.
Numpy doesn't saves memory by fusing of operations.
Numpy doesn't supports vectorized batching of operations
Numpy (mostly python inherently) doesn't supports parallelization of data and computation

Mostly we work with CPU and GPU device data formats by copying the data into device memory, converting it into device format and then running operations on it.

To let numpy work on GPU, several teams came up with their solutions (we won't be discussing them on details):

CuPy and other Cu-Libraries by RAPIDS AI and NVIDIA supports CUDA Array Interface (GPU) instead of Numpy Array Interface (CPU), thus running only on GPU devices.
Numba by Ananconda is a JIT compiler supporting both CUDA Array Interface (GPU) and Numpy Array Interface (CPU) but it transpiles python bytecode directly to LLVM for compilation, thus complicating things.

This copy-and-converting data between different formats is an expensive and incredibly time-consuming task that adds zero value to data science pipelines.

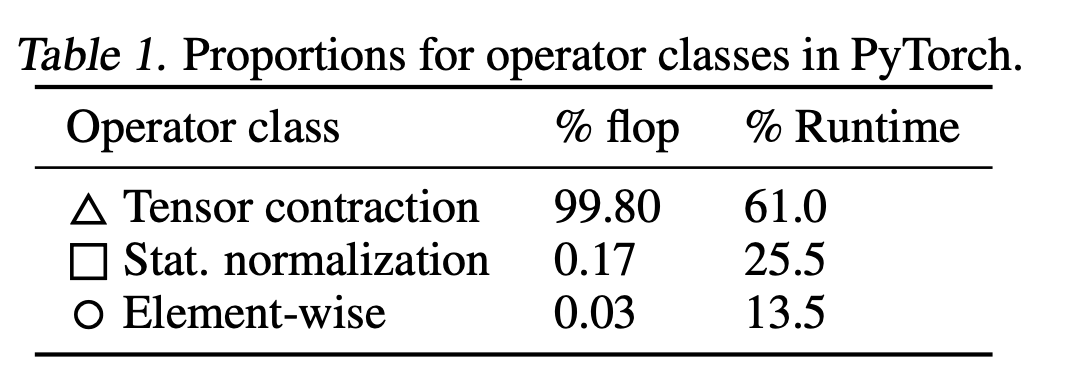
Let's look at a report from this recent paper on FLOP counts on SOTA model like BERT for different operator types: Bert Perf

You can see that altogether, our non-matmul ops only make up 0.2% of our FLOPS, but 40% of our runtimes. These are also called memory-bound operations.

Well, JAX seems like a promising alternative to Numpy, fixing all of above mentioned issues.

JAX is a high performance, numerical computing library which incorporates composable function transformations.

It lies at the intersection of Scientific Computing and Function Transformations, yielding a wide range of capability beyond the ability to train just Deep Learning models.

A function transformation is an operator on a function whose output is another function.

It treates differentiation as first-class citizen
Its hardware accelerator agnostic
Its compiler oriented
It provides numpy like API
And a lot more...

It mainly constitutes of JIT Compilation, Autograd And XLA Compiler

JIT: Just in Time compilation compiles code during execution of the program i.e. during runtime.
Autograd: It provides a framework for general Differentiable Programming.
XLA: Accelerated Linear Algebra is a graph-based, whole-program optimizing compiler, designed specifically for linear algebra. It divides the code into sequence of computation kernels, significantly increases execution speed and lower memory usage by fusing low-level operations. For example: it uses single gpu kernel by fusing addition and multiplication, without writing intermediate values into memory (instead keeping in GPU registers and streaming them).

Deep Learning Community is embracing JAX

Huggingface supports almost all their models in JAX
Deepmind shifted to JAX
Google used JAX with its 4096 cores TPU Supercomputer to win six out of eight MLPerf benchmark competitions.
Recently Google launched LaMDA which too is built on JAX.

In this notebook, we shall go through the powers of JAX.

Install Libraries¶

In [ ]:

!add-apt-repository ppa:longsleep/golang-backports -y
!apt update
!apt install golang-go
%env GOPATH=/root/go

!apt-get install graphviz gv
!go install github.com/google/pprof@latest

In [ ]:

!pip install --upgrade "jax[cuda]" -f https://storage.googleapis.com/jax-releases/jax_cuda_releases.html

Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Looking in links: https://storage.googleapis.com/jax-releases/jax_cuda_releases.html
Requirement already satisfied: jax[cuda] in /usr/local/lib/python3.7/dist-packages (0.3.8)
Requirement already satisfied: scipy>=1.2.1 in /usr/local/lib/python3.7/dist-packages (from jax[cuda]) (1.4.1)
Requirement already satisfied: typing-extensions in /usr/local/lib/python3.7/dist-packages (from jax[cuda]) (4.1.1)
Requirement already satisfied: absl-py in /usr/local/lib/python3.7/dist-packages (from jax[cuda]) (1.1.0)
Requirement already satisfied: opt-einsum in /usr/local/lib/python3.7/dist-packages (from jax[cuda]) (3.3.0)
Requirement already satisfied: numpy>=1.19 in /usr/local/lib/python3.7/dist-packages (from jax[cuda]) (1.21.6)
Collecting jaxlib==0.3.7+cuda11.cudnn82
  Downloading https://storage.googleapis.com/jax-releases/cuda11/jaxlib-0.3.7%2Bcuda11.cudnn82-cp37-none-manylinux2014_x86_64.whl (158.1 MB)
     |████████████████████████████████| 158.1 MB 29 kB/s 
Requirement already satisfied: flatbuffers<3.0,>=1.12 in /usr/local/lib/python3.7/dist-packages (from jaxlib==0.3.7+cuda11.cudnn82->jax[cuda]) (2.0)
Installing collected packages: jaxlib
  Attempting uninstall: jaxlib
    Found existing installation: jaxlib 0.3.7+cuda11.cudnn805
    Uninstalling jaxlib-0.3.7+cuda11.cudnn805:
      Successfully uninstalled jaxlib-0.3.7+cuda11.cudnn805
Successfully installed jaxlib-0.3.7+cuda11.cudnn82

In [ ]:

!nvidia-smi

Tue Jun 21 14:28:48 2022       
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 460.32.03    Driver Version: 460.32.03    CUDA Version: 11.2     |
|-------------------------------+----------------------+----------------------+
| GPU  Name        Persistence-M| Bus-Id        Disp.A | Volatile Uncorr. ECC |
| Fan  Temp  Perf  Pwr:Usage/Cap|         Memory-Usage | GPU-Util  Compute M. |
|                               |                      |               MIG M. |
|===============================+======================+======================|
|   0  Tesla P100-PCIE...  Off  | 00000000:00:04.0 Off |                    0 |
| N/A   36C    P0    26W / 250W |      0MiB / 16280MiB |      0%      Default |
|                               |                      |                  N/A |
+-------------------------------+----------------------+----------------------+
                                                                               
+-----------------------------------------------------------------------------+
| Processes:                                                                  |
|  GPU   GI   CI        PID   Type   Process name                  GPU Memory |
|        ID   ID                                                   Usage      |
|=============================================================================|
|  No running processes found                                                 |
+-----------------------------------------------------------------------------+

In [ ]:

import jax
jax.devices()

Out[ ]:

[GpuDevice(id=0, process_index=0)]

In [ ]:

import jax.numpy as jnp
from jax import random
from jax import grad, jit, make_jaxpr, vmap, pmap
import numpy as np

Syntax same, but BTS lies difference!!¶

In [ ]:

x = np.zeros(10)
x

Out[ ]:

array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

In [ ]:

y = jnp.zeros(10)
y

Out[ ]:

DeviceArray([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)

Unlike Numpy, JAX arrays are immutable, meaning that once created their contents cannot be changed.

In [ ]:

print("Numpy arrays are mutable")
print(f"Earlier memory address: {hex(id(x))}")
x[0] = 10
print(x)
print(f"Current memory address: {hex(id(x))}")
print("\n")
print("JAX cannot be in-place mutated. It returns a copy")
print(f"Earlier memory address: {hex(id(y))}")
y = y.at[0].set(10)
print(y)
print(f"Current memory address: {hex(id(y))}")

Numpy arrays are mutable
Earlier memory address: 0x7fafbda22450
[10.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
Current memory address: 0x7fafbda22450


JAX cannot be in-place mutated. It returns a copy
Earlier memory address: 0x7fafbe3554b0
[10.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
Current memory address: 0x7fafbe355330

Now let's understand JAX via few of its properties

How randomness is handled in JAX¶

In [ ]:

seed = 0
np.random.seed(seed)

print("For Numpy:")
# function def
def bar(): return np.random.uniform()
def car(): return np.random.uniform()

def foo1(): return bar() + 2*car()
print(f"bar + 2 x car gives {foo1()}")

def foo2(): return 2*car() + bar()
print(f"2 x car + bar gives {foo2()}")

For Numpy:
bar + 2 x car gives 1.9791922366721637
2 x car + bar gives 1.7504099351401847

Algorithm is same but the result is different. This is because the order of the execution of the functions is not the same anymore.

This becomes a problem when trying to parallelize all of our complex functions. We cannot guarantee order or their executions and therefore, there is no way of enforcing reproducibility of results we are getting.

JAX solves this by pseudo-random number generator keys.

In [ ]:

state = 101
key = random.PRNGKey(state)

# subkeys for each functions
subkeys = random.split(key, num=2)

print("For JAX:")
# function def
def bar(): return random.uniform(subkeys[0])
def car(): return random.uniform(subkeys[1])

def foo1(): return bar() + 2*car()
print(f"bar + 2 x car gives {foo1()}")

def foo2(): return 2*car() + bar()
print(f"2 x car + bar gives {foo2()}")

For JAX:
bar + 2 x car gives 2.470635175704956
2 x car + bar gives 2.470635175704956

Speed Comparison¶

In [ ]:

x = np.random.rand(10000,10000).astype(np.float32) 
# For fair comparision 
# Numpy defaults tp 64-bit dtypes whule JAX to 32-bit.
y = jnp.array(x)

In [ ]:

%timeit -n 1 -r 1 np.dot(x,x)

1 loop, best of 1: 22.1 s per loop

In [ ]:

%timeit -n 1 -r 1 jnp.dot(y,y).block_until_ready()

1 loop, best of 1: 3.62 s per loop

We are using block_until_ready for benchmarking for a reason we are about to cover. JAX compiles and caches it in the device memory. So next time you run the same operation, it gives results much faster.

Its 7-8 times faster.

In [ ]:

%timeit -n 1 -r 1 jnp.dot(y,y).block_until_ready()

1 loop, best of 1: 229 ms per loop

Its 100x faster. Impressive, but watch this - let's remove block until ready.

In [ ]:

%timeit -n 1 -r 1 jnp.dot(y,y)

1 loop, best of 1: 931 µs per loop

Micro seconds for 10k dim x 10k dim matrix multiplication on single NVIDIA TESLA P100 GPU of 16GB RAM, isn't that suprising?

Let's understand why.

Asynchronous Dispatch¶

JAX is async. What happened earlier was that JAX mislead us when we removed block until ready. We were not timing the execution of matrix multiplication, only the time to dispatch the work. To measure the true cost of operation, we need to wait untill the execution is complete in order to properly measure the time. So we use block until ready during benchmarking.

Explaination:

JAX does not wait for the operation to complete before returning control to the Python program. Instead, JAX returns a DeviceArray value, which is a future, i.e., a value that will be produced in the future on an accelerator device but isn’t necessarily available immediately. We can inspect the shape or type of a DeviceArray without waiting for the computation that produced it to complete, and we can even pass it to another JAX computation, as we do with the addition operation here. Only if we actually inspect the value of the array from the host, for example by printing it or by converting it into a plain old numpy.ndarray will JAX force the Python code to wait for the computation to complete.

Asynchronous dispatch is useful since it allows Python code to “run ahead” of an accelerator device, keeping Python code out of the critical path. Provided the Python code enqueues work on the device faster than it can be executed, and provided that the Python code does not actually need to inspect the output of a computation on the host, then a Python program can enqueue arbitrary amounts of work and avoid having the accelerator wait.

Let's breakdown the earlier operation:

In [ ]:

# instead of using .dot function let's user define it
def f(x):  
  return x @ x

In [ ]:

# measure NumPy runtime
x_np = np.random.rand(10000,10000).astype(np.float32) 
%timeit -n 1 -r 1 f(x_np)

1 loop, best of 1: 22.4 s per loop

NumPy takes around 20 s per evaluation on the CPU

In [ ]:

# measure JAX device transfer time
%time x_jax = jax.device_put(x_np)

CPU times: user 9 ms, sys: 1.02 ms, total: 10 ms
Wall time: 9.52 ms

JAX takes around 5 ms to copy the NumPy arrays onto the GPU

In [ ]:

# measure JAX compilation time
f_jit = jit(f)
%time f_jit(x_jax).block_until_ready()

CPU times: user 92.5 ms, sys: 48 ms, total: 140 ms
Wall time: 352 ms

Out[ ]:

DeviceArray([[2489.3577, 2463.2961, 2486.5251, ..., 2468.2246, 2485.337 ,
              2486.9387],
             [2515.0486, 2532.0928, 2548.9595, ..., 2523.4004, 2516.9792,
              2537.574 ],
             [2513.7805, 2521.4624, 2540.517 , ..., 2508.0244, 2507.6   ,
              2521.0579],
             ...,
             [2485.6765, 2488.7998, 2513.743 , ..., 2491.3413, 2475.7664,
              2484.1887],
             [2493.5042, 2491.062 , 2519.9312, ..., 2481.506 , 2483.618 ,
              2498.8936],
             [2495.9058, 2481.7222, 2509.2488, ..., 2477.701 , 2462.4023,
              2485.2917]], dtype=float32)

JAX takes around 300 ms to compile the function

In [ ]:

# measure JAX runtime
%timeit -n 1 -r 1 f_jit(x_jax).block_until_ready()

1 loop, best of 1: 229 ms per loop

JAX takes 200 ms per evaluation on the GPU.

In this case, we see that once the data is transfered and the function is compiled, JAX on the GPU is about 100x faster for repeated evaluations.

Is this a fair comparison on speed? Maybe. The performance that ultimately matters is for running full deep learning applications, which inevitably include some amount of both data transfer and compilation.

Did you notice jit?

JAX incorporates an extensible system for such function transformations, and has four main transformations of interest to the typical user:

jit() to transform functions into just-in-time compiled versions
grad() for evaluating the gradient function of the input function
vmap() for automatic vectorization of operations
pmap() for easy parallelization of computations

JIT Compilation¶

NumPy operations are executed eagerly, synchronously, and only on CPU.
By default JAX executes operations one at a time, in sequence or eagerly, and dispatches asynchronously on all devices CPU/GPU/TPU. Using just-in-time (JIT) compilation, sequences of operations can be optimized together and run at once. JAX uses the XLA compiler to execute blocks of code very efficiently.

But there is a catch - Not all JAX code can be JIT compiled, as it requires array shapes to be static & known at compile time. For ex: shape is not known for x for def f(x): return x[x<0] during compile time.

Let's understand how jit works.

In [ ]:

# Let's first see how numpy works
def f(x, y):
  print("Running f():")
  print(f"  x = {x}\n")
  print(f"  y = {y}\n")
  result = np.dot(x + 1, y + 1)
  print(f"  result = {result}\n")
  return result

x = np.random.randn(3, 4)
y = np.random.randn(4, 1)
f(x, y)

Running f():
  x = [[-0.35960949  1.52744007 -0.44154394  0.02519481]
 [-0.57144428 -1.52495174  0.72102243 -0.21198663]
 [ 0.60934449 -1.01884849 -0.74926673  0.05947864]]

  y = [[-1.06645266]
 [-0.26044164]
 [-1.17089024]
 [ 0.60112815]]

  result = [[3.37266737]
 [0.55089334]
 [1.53262843]]

Out[ ]:

array([[3.37266737],
       [0.55089334],
       [1.53262843]])

In [ ]:

def f(x, y):
  print("Running f():")
  print(f"  x = {x}")
  print(f"  y = {y}")
  result = jnp.dot(x + 1, y + 1)
  print(f"  result = {result}\n")
  return result

x = random.normal(key, (3, 4))
y = random.normal(key, (4, 1))
f_jit = jit(f)
f_jit(x, y)

Running f():
  x = Traced<ShapedArray(float32[3,4])>with<DynamicJaxprTrace(level=0/1)>
  y = Traced<ShapedArray(float32[4,1])>with<DynamicJaxprTrace(level=0/1)>
  result = Traced<ShapedArray(float32[3,1])>with<DynamicJaxprTrace(level=0/1)>

Out[ ]:

DeviceArray([[3.83735  ],
             [1.4746052],
             [5.683498 ]], dtype=float32)

Notice that rather than printing the data we passed to the function, it prints tracer objects that stand-in for them.

These tracer objects are what jit uses to extract the sequence of operations specified by the function. Basic tracers are stand-ins that encode the shape and dtype of the arrays, but are agnostic to the values. This recorded sequence of computations can then be efficiently applied within XLA to new inputs with the same shape and dtype, without having to re-execute the Python code.

Let's call the compiled function again on another input value but having same shape and dtype.

In [ ]:

key2 = random.PRNGKey(202)
x2 = random.normal(key2, (3, 4))
y2 = random.normal(key2, (4, 1))
f_jit(x2, y2)

Out[ ]:

DeviceArray([[6.8841944],
             [8.1478615],
             [5.9593167]], dtype=float32)

Did you notice print statements didn't run. Which means it didn't re-compile. It's because the result is computed in compiled XLA rather than in Python.

You can view the sequence of operations encoded in a JAX expression using the jax.make_jaxpr transformation:

In [ ]:

def f(x, y):
  return jnp.dot(x + 1, y + 1)

make_jaxpr(f)(x, y)

Out[ ]:

{ lambda ; a:f32[3,4] b:f32[4,1]. let
    c:f32[3,4] = add a 1.0
    d:f32[4,1] = add b 1.0
    e:f32[3,1] = dot_general[
      dimension_numbers=(((1,), (0,)), ((), ()))
      precision=None
      preferred_element_type=None
    ] c d
  in (e,) }

Remember:

Static Manner: Numpy executes operations only once at compile-time.
Traced Manner: JAX optimizes, compiles and executes operations at run-time.

And ya, JIT is faster than default.

In [ ]:

x = random.normal(key, (1000, 1000))

def f(x):
    for _ in range(10):
        x = 0.5*x + 0.1*jnp.sin(x)
    return x

g = jit(f)

In [ ]:

%timeit -n 1 -r 5 f(x).block_until_ready()

The slowest run took 83.29 times longer than the fastest. This could mean that an intermediate result is being cached.
1 loop, best of 5: 3.19 ms per loop

In [ ]:

%timeit -n 1 -r 5 g(x).block_until_ready()

The slowest run took 976.31 times longer than the fastest. This could mean that an intermediate result is being cached.
1 loop, best of 5: 229 µs per loop

Almost 30 times faster. \m/

Auto differentiation with grad()¶

Scalar-Valued Functions¶

Here we are looking for Gradient

For example,

gradient of $3x^2 + 2x + 5$ is $6x +2$

In [ ]:

def f(x):
    return 3*x**2 + 2*x + 5

# derivative of f at 1
print(grad(f)(1.0))

8.0

Vector-Valued Functions¶

Here we are looking for Jacobian

Ex: For vector [x*x, y*z], its jacobian is

[[d/dx x^2 , d/dy x^2, d/dz x^2]
[d/dx y*z , d/dy y*z, d/dz y*z]]

which reduces to

[[2*x, 0, 0]
[0, z, y]]

Let's code.

In [ ]:

from jax import jacfwd, jacrev, hessian
# forward mode differentiation, reverse mode differentiation, hessian

def vec_f(v):
  x = v[0]
  y = v[1]
  z = v[2]
  return jnp.array([x*x, y*z])

v = jnp.array([4., 5., 9.])
f = jacfwd(vec_f)
print(f(v))

[[8. 0. 0.]
 [0. 9. 5.]]

Hessians - Matrix of second order mixed partials¶

JAX makes computing Hessians exceedingly easy and efficient. Because of XLA, it can compute Hessians remarkably faster than PyTorch, which makes it much more practical to implement higher-order optimization techniques like AdaHessian.

In [ ]:

import torch as pt

def torch_fn(X):
  return pt.sum(pt.mul(X,X))
  
X = pt.randn((1000,))

%timeit -n 10 -r 5 pt.autograd.functional.hessian(torch_fn, X, vectorize=True)

10 loops, best of 5: 2.83 ms per loop

In [ ]:

def jax_fn(X):
  return jnp.sum(jnp.square(X))

jit_jax_fn = jit(hessian(jax_fn))

X = jnp.array(X)

%timeit -n 10 -r 5 jit_jax_fn(X).block_until_ready()

The slowest run took 43.66 times longer than the fastest. This could mean that an intermediate result is being cached.
10 loops, best of 5: 100 µs per loop

Almost 30 times faster!!

Automatic vectorization with Vmap¶

We can take a function that operates on a single data point and vectorize it so it can accept a batch of these data points (or a vector) of arbitrary size. It basically promotes matrix-vector products into matrix-matrix products.

Consider the task of adding two array

Watch the difference:

Unvectorized Vector Addition

Vectorized Vector Addition

In [ ]:

def f(x):
  return x * x

In [ ]:

%timeit -n 1 -r 5 jnp.stack([f(x) for x in jnp.arange(10000)]).block_until_ready()

1 loop, best of 5: 2.87 s per loop

In [ ]:

f_jit = jit(f)
%timeit -n 1 -r 5 jnp.stack([f_jit(x) for x in jnp.arange(10000)]).block_until_ready()

1 loop, best of 5: 2.9 s per loop

In [ ]:

%timeit -n 1 -r 5  vmap(f)(jnp.arange(10000)).block_until_ready()

The slowest run took 90.71 times longer than the fastest. This could mean that an intermediate result is being cached.
1 loop, best of 5: 839 µs per loop

In [ ]:

%timeit -n 1 -r 5  vmap(f_jit)(jnp.arange(10000)).block_until_ready()

The slowest run took 101.37 times longer than the fastest. This could mean that an intermediate result is being cached.
1 loop, best of 5: 688 µs per loop

Almost 400 times faster \m/

SPMD Programming with Pmap¶

Consider the example of vector-matrix multiplication.

Watch the difference:

Unparallelized vector-matrix multiplication

Parallelized vector-matrix multiplication

Check JAX TPU Notebook.

Device Memory Profiler¶

JAX’s built-in Device Memory Profiler, provides visibility into how the JAX code executes on GPUs and TPUs.

In [ ]:

import jax.profiler

def func1(x):
  return jnp.tile(x, 10) * 0.5

def func2(x):
  y = func1(x)
  return y, jnp.tile(x, 10) + 1

x = jax.random.normal(jax.random.PRNGKey(42), (1000, 1000))
y, z = func2(x)

z.block_until_ready()
jax.profiler.save_device_memory_profile("memory.prof")

In [ ]:

!go tool pprof -png memory.prof

Main binary filename not available.
Generating report in profile001.png

Overview:¶

JAX is easy to use with Numpy like API and is device agnostic
JAX is fast and easily parallelizable
Robust and powerful function transformations
Functional programming model which aligns well with maths, and are easier to debug and produce reproducible results.
It's still in dev mode, not officially released.
Its good for research purpose, but if you want to fast explore the JAX's deep learning capabilities try Flex or Haiku, built on JAX.

Are you convinced regarding awesomness of JAX?

If you love python, here's a fun fact you may like to know:

Numpy: 62.3% Python, 35.3% C
Pytorch: 52.4% C++, 37.4% Python
Tensorflow: 62.7% C++, 22.2% Python
Julia: 68.4% Julia, 16.4% C, 10.1% C++
Jax: 92.7% Python
Flax: 98.1% Python

Next - Train deep learning models using Flax/Haiku