MIT Licence

© Alexey A. Shcherbakov, 2024

Lecture 2.1. Photonic crystals. Properties and applications¶

Photonic crystals¶

A photonic crystal is a periodic structure in one, two, or three dimensions in which the material parameters relating the fields in the material equations for the electromagnetic field change periodically. In the theoretical description of photonic crystals, one usually starts by considering an infinite periodic structure that fills the entire space. In practice, examples of photonic crystals include periodic multilayers - Bragg gratings (one-dimensional), - etched long cylindrical cavities or periodically arranged cylinders on a substrate (two-dimensional), and artificial opals (three-dimensional). Profiled one-dimensional and two-dimensional diffraction gratings whose material distribution is invariant along the depth can also be considered as layers of corresponding photonic crystals.

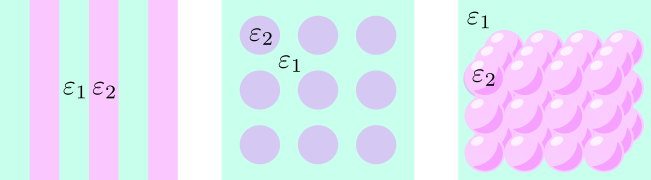
The terminology of photonic crystals has arisen from analogy with the terminology of a branch of the solid state physics where periodic potentials are considered. Electrons in solid crystalline solids can be described using the zone theory. Such concepts as inverse lattice, Brillouin zones, forbidden zone appear in the optics of periodic media as well. Thus, for example, in photonic crystals it is possible to find frequency intervals in which there are no propagating eigen solutions, in other words, all waves excited within these intervals will be evanescent. Such intervals are called band gaps. The possibility of formation of band gaps for all possible electromagnetic waves in a crystal shows its essential difference from free isotropic or anisotropic space. Therefore, one can expect a significant change in the characteristics of various sources of electromagnetic radiation placed inside or near photonic-crystal structures. Another direction of application of the special properties of photonic crystals is the creation of high-frequency resonators and waveguides by introducing defects into the ideal lattice. In this case, if all optical materials of which the photonic crystal consists are dielectric, the quality factor of such resonators can be very high.

Band gap¶

Let us consider some general electromagnetic properties of photonic crystals. In the simplest one-dimensional case of nonmagnetic media, the eigen equation in the crystal is the scalar Helmholtz equation \begin{equation}\tag{1} \left[\frac{d^2}{dz^2} + \omega^2\varepsilon(z)\mu_0\right] E(z) = 0 \end{equation} with the periodic function $\varepsilon(z+n\Lambda) = \varepsilon(z)$, where $\Lambda$ is the crystal period. According to the Floquet-Bloch's theorem, the field in a periodic potential is represented as a product of the Floquet-Bloch exponent by a periodic function. Let us decompose the latter into its Fourier series, so that \begin{equation}\tag{2} E(z) = e^{ik_0z} u(z) = e^{ik_0z} \sum_{m=-\infty}^{\infty} u_m \exp(2\pi im z/\Lambda). \end{equation} The set of points $mK = 2\pi im/\Lambda$ defines a grid in the reciprocal space, where the region $-K/2\leq k\leq K/2$ is called the first Brillouin zone. Let us multiply equation (1) by the inverse dielectric permittivity function and decompose this function into its Fourier series. For simplicity, we assume that the first three terms make the main contribution to the series, so that \begin{equation}\tag{3} \varepsilon^{-1}(z) = \sum_{m=-\infty}^{\infty} \zeta_m \exp(2\pi im z/\Lambda) \approx \zeta_0 + \zeta_1 e^{2\pi i z/\Lambda} + \zeta_{-1} e^{-2\pi i z/\Lambda}. \end{equation} Substituting (2) and (3) into (1) and using the orthogonality of exponential functions, we obtain a system of coupled equations \begin{equation}\tag{4} \zeta_1 \left[ k_0 + \frac{2\pi}{\Lambda}(m-1) \right]^2 u_{m-1} + \zeta_{-1} \left[ k_0 + \frac{2\pi}{\Lambda}(m+1) \right]^2 u_{m+1} \approx \left[ \omega^2\mu_0 - \zeta_0 \left(k_0 + \frac{2\pi}{\Lambda}m\right)^2 \right] u_{m} \end{equation} Let us write the equations for $m=0,\pm1$ and consider the values of the Bloch vector at the edge of the first Brillouin zone $k_0\approx K/2$. If the the dielectric permittivity is close to a one of a free isotropic space, we can also assume that at most points of k-space the dispersion is not very different from the dispersion of the free space $\omega^2\mu_0\approx \zeta_0 k_0^2$. Under these conditions, it can be shown that the main contribution to the field is made by the summands with $m=0,1$. Neglecting all other terms in (4), we obtain a system of two equations \begin{equation*} \begin{array}{c} \left( \omega^2\mu_0 - \zeta_0 k_0^2 \right) u_{0} - \zeta_1 \left( k_0 - \frac{2\pi}{\Lambda} \right)^2 u_{-1} \approx 0 \\ -\zeta_{-1} k_0^2 u_{0} + \left[ \omega^2\mu_0 - \zeta_0 \left(k_0 - \frac{2\pi}{\Lambda}\right)^2 \right] u_{-1} \approx 0 \end{array} \end{equation*} We denote $\Delta k = k-\pi/\Lambda$, so that $|\Delta k|\ll \pi/\Lambda$. Equating the determinant of the system to zero and solving with respect to the eigne frequency, we find two solutions \begin{equation*} \omega_{\pm} \approx \frac{K}{2} \sqrt{\zeta_0\pm|\zeta_1|} \pm \frac{1}{\sqrt{\zeta_0}|\zeta_1|} \frac{(\Delta k)^2}{K/2} \left( \zeta_0^2 -\frac{\zeta_1^2}{4} \right) \end{equation*} The band gap excists in the frequency range $(K/2)\sqrt{\zeta_0-|\zeta_1|} < \omega < (K/2)\sqrt{\zeta_0+|\zeta_1|}$.

In the absence of modulation $\zeta_m=0$ for all $m\neq0$ and the forbidden zone vanishes - the so-called empty lattice approximation is obtained. At non-zero modulation there is an infinite number of band gaps - the estimate for the lowest one is given above. Pairs of coincident solutions corresponding to intersections of dispersion lines in the empty lattice approach are split. Since, in the presence of periodicity, the solutions differing by $K=2\pi/\Lambda$ are equivalent, the solutions at the edges of the Brillouin zones correspond to the interference of waves propagating in opposite directions, which leads to the formation of standing waves whose group velocity $v_g = d\omega/dk_0$ is zero, and, therefore, the tangent to the dispersion curve $\omega(k_0)$ at the boundaries has a zero angle of inclination.

Group velocity anomaly¶

In the case of two-dimensional crystals, there are two noncollinear periodicity directions and, accordingly, two basis vectors of the reciprocal lattice. The first Brillouin zone is a two-dimensional Wigner-Seitz cell in reciprocal space. The high symmetry points of this zone are usually denoted by capitalized Greek letters. The center of the first Brillouin zone is called the $\Gamma$-point. Dispersion diagrams are often shown with with lines corresponding to direct trajectories connecting the points of high symmetry.

In the empty lattice approximation the disperion is defined by the equation \begin{equation}\tag{5} \left(k_x + mK_x\right)^2 + \left(k_y + nK_y\right)^2 = \omega^2\varepsilon\mu_0 \end{equation} For example, for a square lattice, the two periods are given by the vectors $\boldsymbol{p}_1 = (\Lambda,0)^T$ and $\boldsymbol{p}_2 = (0,\Lambda)^T$. Corresponding reciprocal lattice vectors are $\boldsymbol{K}_1 = (2\pi/\Lambda,0)^T$ and $\boldsymbol{K}_2 = (0,2\pi/\Lambda)^T$. The trajectory $\Gamma X$ is given by changing the vector $\boldsymbol{k} = (k_x,0)^T$. For the third zone with $m=2$, it can be seen that along the entire trajectory the slope of the dispersion curve remains small, which corresponds to the small group velocity of the waves. This effect is called the group velocity anomaly. Some research have demonstrated the structures of photonic crystals that allow the appearance of dispersion bands with almost zero group velocity.

Scaling and time reversal symmetry¶

If we normalize the wavevectors by the modulus of the inverse lattice vector $\boldsymbol{k}\rightarrow (1/K) \boldsymbol{k} = (\Lambda/2\pi) \boldsymbol{k}$, and the frequency is measured in units of $2\pi c/\Lambda$, the electromagnetic properties of photonic crystals as solutions of Maxwell's equations will remain the same under the condition that the values of material parameters are not changed. This follows from the substitution into the equations of the coordinates and time normalized by the period and $\Lambda/c$, respectively. This property is called scaling.

The wave equation is independent of the time sign change $t'=-t$, therefore, the solution $\tilde{\boldsymbol{E}}(\boldsymbol{r},t') = \boldsymbol{E}(\boldsymbol{r},-t)$ also satisfies this equation. Consequently, the eigenfrequencies of $\omega_{\boldsymbol{k}n}$, which the solutions to the eigenvalue problem, remain the same. Then, \begin{equation*} \tilde{\boldsymbol{E}}(\boldsymbol{r},t') = \boldsymbol{u}_{\boldsymbol{k}n}(\boldsymbol{r}) \exp[i(\boldsymbol{k}\boldsymbol{r} - \omega_{\boldsymbol{k}n}t')] \end{equation*} Inverse transformation gives \begin{equation*} \boldsymbol{E}(\boldsymbol{r},t) = \left( \boldsymbol{u}^*_{\boldsymbol{k}n}(\boldsymbol{r}) \exp[i(-\boldsymbol{k}\boldsymbol{r} - \omega_{\boldsymbol{k}n}t)] \right)^* \end{equation*} Since the measured field is the real part of a complex-valued solution, it can be seen that \begin{equation}\tag{6} \begin{array}{c} \omega_{-\boldsymbol{k}n} = \omega_{\boldsymbol{k}n}, \\ \boldsymbol{u}_{-\boldsymbol{k}n} = \boldsymbol{u}^*_{\boldsymbol{k}n} \end{array} \end{equation} This implies the symmetry of the dispersion diagrams with respect to the inversion in the reciprocal space.

References¶

1. K. Sakoda, Optical Properties of Photonic Crystals, Springer Science & Business Media (2004)
2. J.D. Joannopoulos, S.G. Johnson, J.N. Winn, and R.D. Meade, Photonic Crystals. Molding the Flow of Light (Second Edition), Princeton University Press (2011)