Лекция 1.2. Методы S- и Т-матриц¶

На данной лекции будет проведена аналогия между коэффициентами Френеля и Ми, введены матрицы рассеяния и прохождения, а также рассмотрены алгоритмы расчета оптических свойств многослойных структур с простыми границами и сред, сводящимся к таким структурам.

Отражение и преломление на плоской границе¶

В областях вне источников в однородном изотропном пространстве поле в декартовых координатах может быть разложено на волны двух ортогональных поляризаций, 's' и 'p', относительно выделенной в пространстве декартовой оси $Z$. При этом волны разделяются по направлению распространения относительно этой оси, что соответствует двум типам решений дисперсионного уравнения, и ниже обозначется верхним индексом $\sigma=\pm$. Обозначим амплитуды электрического поля 's'-поляризации как $a^{s\sigma}$, а амплитуды магнитного поля 'p'-поляризации как $a^{p\sigma}$. Тогда из закона Фарадея и теоремы о циркуляции магнитного поля получаем \begin{align*} \boldsymbol{E}^{s\sigma} &= a^{s\sigma} \hat{\boldsymbol{e}}^{s\sigma} \Rightarrow \boldsymbol{H}^{s\sigma} = \dfrac{1}{\omega\mu}\boldsymbol{k}^{\sigma} \times \boldsymbol{E}^{s\sigma} = \dfrac{k}{\omega\mu} a^{s\sigma} \hat{\boldsymbol{e}}^{p\sigma} \\ \boldsymbol{H}^{p\sigma} &= a^{p\sigma} \hat{\boldsymbol{e}}^{s\sigma} \Rightarrow \boldsymbol{E}^{p\sigma} = -\dfrac{1}{\omega\varepsilon}\boldsymbol{k}^{\sigma} \times \boldsymbol{H}^{p\sigma} = -\dfrac{k}{\omega\varepsilon} a^{p\sigma} \hat{\boldsymbol{e}}^{p\sigma} \end{align*} а разложение поле в области, свободной от источников имеет вид \begin{equation*} \left( \begin{array}{c} \boldsymbol{E}\left(\boldsymbol{r}\right) \\ \boldsymbol{H}\left(\boldsymbol{r} \right) \end{array} \right) = \iint_{-\infty}^{\infty} dk_{x}dk_{y} e^{i\boldsymbol{\rho}\boldsymbol{\varkappa}} \sum_{\sigma=\pm} \left( \! \begin{array}{c} a^{s\sigma}_{\boldsymbol{k}} \hat{\boldsymbol{e}}^{s\sigma}_{\boldsymbol{k}} - \dfrac{k}{\omega\varepsilon} a^{p\sigma}_{\boldsymbol{k}} \hat{\boldsymbol{e}}^{p\sigma}_{\boldsymbol{k}} \\ a^{p\sigma}_{\boldsymbol{k}} \hat{\boldsymbol{e}}^{s\sigma}_{\boldsymbol{k}} + \dfrac{k}{\omega\mu} a^{s\sigma}_{\boldsymbol{k}} \hat{\boldsymbol{e}}^{p\sigma}_{\boldsymbol{k}} \end{array} \! \right) e^{\sigma ik_{z}z} \end{equation*} где $\boldsymbol{\rho} = (x,y)^T$, и $\boldsymbol{\varkappa} = (k_x,k_y)^T$. Это выражение справедливо, как во всем однородном пространстве, так, например, и в полупространстве или слое, ограниченными плоскими границами $z=const$.

Пусть теперь плоская граница с координатой $z=0$ разделяет два однородных изотропных полупространства, каждое имеющее свои материальные константы $\varepsilon_{1,2}$, $\mu_{1,2}$ и соответствующие им волновые числа $k_{1,2}=\omega\sqrt{\varepsilon_{1,2}\mu_{1,2}}$. Условие сопряжения на границе (непрерывность тангенциальных компонент полей) имеет вид \begin{equation*} E_{x,y}(\boldsymbol{\rho},-0) = E_{x,y}(\boldsymbol{\rho},+0), \; H_{x,y}(\boldsymbol{\rho},-0) = H_{x,y}(\boldsymbol{\rho},+0) \end{equation*} Обозначим амплитуды разложения полей по плоским волнам в первой среде при $z < 0$ как $b^{P\sigma}_{\boldsymbol{k}}$, и во второй среде при $z > 0$ как $a^{P\sigma}_{\boldsymbol{k}}$, где $P=s,p$ обозначает состояние поляризации.

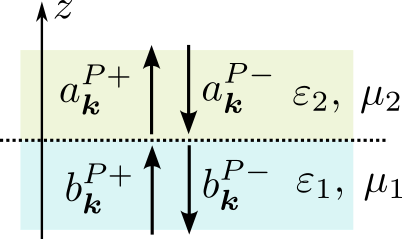
Без ограничения общности можно положить $k_y=0$ (проекция волнового числа/импульса волны в плоскости $XY$ сохраняется). Тогда условия сопряжения и ортогональность экспоненциальных множителей $\exp(i\boldsymbol{\varkappa}\boldsymbol{\rho})$ приводят к равенствам \begin{align*} \left( b_{\boldsymbol{k}}^{s+} + b_{\boldsymbol{k}}^{s-} \right) \hat{\boldsymbol{e}}_{y} + \frac{k_{z1}}{\omega\varepsilon_{1}} \left( b_{\boldsymbol{k}}^{p+} - b_{\boldsymbol{k}}^{p-} \right) \hat{\boldsymbol{e}}_{x} &= \left( a_{\boldsymbol{k}}^{s+} + a_{\boldsymbol{k}}^{s-} \right) \hat{\boldsymbol{e}}_{y} + \frac{k_{z2}}{\omega\varepsilon_{2}} \left( a_{\boldsymbol{k}}^{p+} - a_{\boldsymbol{k}}^{p-} \right) \hat{\boldsymbol{e}}_{x} \\ \left( b_{\boldsymbol{k}}^{p+} + b_{\boldsymbol{k}}^{p-}\right) \hat{\boldsymbol{e}}_{y}-\dfrac{k_{z1}}{\omega\mu_{1}}\left(b_{\boldsymbol{k}}^{s+} - b_{\boldsymbol{k}}^{s-}\right)\hat{\boldsymbol{e}}_{x} &= \left(a_{\boldsymbol{k}}^{p+}+a_{\boldsymbol{k}}^{p-}\right) \hat{\boldsymbol{e}}_{y}-\dfrac{k_{z2}}{\omega\mu_{2}}\left(a_{\boldsymbol{k}}^{s+}-a_{\boldsymbol{k}}^{s-}\right)\hat{\boldsymbol{e}}_{x} \end{align*} откуда следует связь между коэффициентами разложения поля по плоским волнам по обе стороны границы раздела сред. Эту связь можно записать в форме, одинаковой для обеих поляризаций, если ввести переменную $\eta$ такую, что $\eta\equiv\mu$ для 's'-поляризации и $\eta\equiv\varepsilon$ для 'p'-поляризации. Выразим амплитуды волн, распространяющихся от границы раздела $a^+$, $b^-$ через амплитуды полн, падающих на границу $a^-$, $b^+$ (нижний индекс также опускаем, поскольку соотношения диагональны по проекции волнового вектора на плоскость $XY$): \begin{equation*} \left( \! \begin{array}{c} b^- \\ a^+ \end{array} \! \right) = \left( \! \begin{array}{cc} r_{11} & t_{12} \\ t_{21} & r_{22} \end{array} \! \right) \left( \! \begin{array}{c} b^+ \\ a^- \end{array} \! \right) = S \left( \! \begin{array}{c} b^+ \\ a^- \end{array} \! \right) \end{equation*} где коэффициенты матрицы $S$ являются амплитудными коэффициентами отражения и прохождения Френеля, а матрица называется матрицей рассеяния или $S$-матрицей. В явном виде \begin{align*} r_{11} &= \dfrac{\eta_{2}k_{z1}-\eta_{1}k_{z2}}{\eta_{1}k_{z2}+\eta_{2}k_{z1}} \\ t_{12} &= \dfrac{2\eta_{1}k_{z2}}{\eta_{1}k_{z2}+\eta_{2}k_{z1}} = 1-r_{11} \\ t_{21} &= \dfrac{2\eta_{2}k_{z1}}{\eta_{1}k_{z2}+\eta_{2}k_{z1}} = 1+r_{11} \\ r_{22} &= \dfrac{\eta_{1}k_{z2}-\eta_{2}k_{z1}}{\eta_{1}k_{z2}+\eta_{2}k_{z1}} = -r_{11} \end{align*} Удобство записи этих коэффициентов через проекции волнового вектора на ось $Z$ состоит в том, что такая форма не изменяется для всех возможных случаев прохождения через границу, включая, неоднородные волны и комплексные значения материальных параметров.

Соотношение между амплитудами можно записать по-другому, в форме T-матрицы, которая связывает амплитуды с одной стороны границы раздела с амплитудами с другой стороны: \begin{equation*} \left( \! \begin{array}{c} a^- \\ a^+ \end{array} \! \right) = T \left( \! \begin{array}{c} b^- \\ b^+ \end{array} \! \right) \end{equation*} В явном виде \begin{align*} T_{11} = T_{22} &= \frac{1}{2} \left( 1+\dfrac{\eta_{1}k_{z2}}{\eta_{2}k_{z1}} \right) \\ T_{12} = T_{21} &= \frac{1}{2} \left( \dfrac{\eta_{1}k_{z2}}{\eta_{2}k_{z1}}-1 \right) \end{align*} Заметим, что T-матрицу также часто определяют не через соотношение между амплитудами плоских волн, а через соотношение между амплитудами проекций электрического и магнитного поля на оси $X,Y$.

Отражение и преломление на сферической границе¶

Теперь рассмотрим сферически симметричный случай и проведем аналогичный вывод для сферических волн. Разложение произвольного монохроматического поля через векторные сферические волны в объеме однородной изотропной среды без источников запишем как \begin{align*} \boldsymbol{E}(k\boldsymbol{r}) &= \sum_{m,n}\sum_{\sigma=1,3} \left[ a^{\sigma}_{mn} \boldsymbol{M}^{\sigma}_{mn}(k\boldsymbol{r}) + b^{\sigma}_{mn} \boldsymbol{N}^{\sigma}_{mn}(k\boldsymbol{r}) \right] \\ \boldsymbol{H}(k\boldsymbol{r}) = \dfrac{i}{\omega\mu} \nabla \times {\boldsymbol E}(k\boldsymbol{r}) &= \dfrac{ik}{\omega\mu} \sum_{m,n} \sum_{\sigma=1,3} \left[ b^{\sigma}_{mn} \boldsymbol{M}^{\sigma}_{mn}(k\boldsymbol{r}) + a^{\sigma}_{mn} \boldsymbol{N}^{\sigma}_{mn}(k\boldsymbol{r}) \right] \end{align*} Это определение отличается от разложения по плоским волнам в том смысле, что для обеих поляризаций $a^{\sigma}_{mn},b^{\sigma}_{mn}$ обозначают амплитуды электрического поля. Здесь необходимо отметить, что, если область пространства, где в таком виде записывается поле, включает начало координат (точку $r=0$), то в разложении должны отсутствовать члены с раходящимися в нуле сферическими волнами, то есть, нужно положить $a^{3}_{mn}\equiv0$. Поле в однородной изотропной области пространства без источников должно быть конечно.

Пусть сферическая граница $r = R$ разделяет две однородные изотропные среды с материальными константами $\varepsilon_{1,2}$, $\mu_{1,2}$, расположенные вблизи этой границы. Внутренняя область может как включать начало координат, так и нет. Запишем условия сопряжения \begin{equation*} E_{\theta,\phi}(R-0,\theta,\phi) = E_{\theta,\phi}(R+0,\theta,\phi), \; H_{\theta,\phi}(R-0,\theta,\phi) = H_{\theta,\phi}(R+0,\theta,\phi) \end{equation*} Подставим явное выражение компонент полей через явный вид проекций векторных сферических волн на единичные векторы сферической системы координат, проинтегрируем по угловым координатам и воспользуемся ортогональностью сферических гармоник. Компоненты, соответствующие разным поляризациям, разделятся. Обозначим амплитуды вблизи границы для $r<R$ с помощью верхнего индекса $(1)$, для $r>R$ с помощью верхнего индекса $(2)$. \begin{align*} a_{nm}^{(1)1}j_{n}\left(k_{1}R\right) - a_{nm}^{(2)3}h_{n}^{(1)}\left(k_{2}R\right) &= a_{nm}^{(2)1}j_{n}\left(k_{2}R\right) - a_{nm}^{(1)3}h_{n}^{(1)}\left(k_{1}R\right) \\ \dfrac{\mu_{2}}{\mu_{1}}a_{nm}^{(1)1}\tilde{j}_{n}\left(k_{1}R\right) - a_{nm}^{(2)3}\tilde{h}_{n}^{(1)}\left(k_{2}R\right) &= a_{nm}^{(2)1}\tilde{j}_{n}\left(k_{2}R\right) - \dfrac{\mu_{2}}{\mu_{1}}a_{nm}^{(1)3}\tilde{h}_{n}^{(1)}\left(k_{1}R\right) \\ b_{nm}^{(1)1}\tilde{j}_{n}\left(k_{1}R\right) - b_{nm}^{(2)3}\dfrac{k_{1}}{k_{2}}\tilde{h}_{n}^{(1)}\left(k_{2}R\right) &= b_{nm}^{(2)1}\dfrac{k_{1}}{k_{2}}\tilde{j}_{n}\left(k_{2}R\right) - b_{nm}^{(1)3}\tilde{h}_{n}^{(1)}\left(k_{1}R\right) \\ b_{nm}^{(1)1}\dfrac{k_{1}}{k_{2}}\dfrac{\mu_{2}}{\mu_{1}}j_{n}\left(k_{1}R\right) - b_{nm}^{(2)3}h_{n}^{(1)}\left(k_{2}R\right) &= b_{nm}^{(2)1}j_{n}\left(k_{2}R\right) - b_{nm}^{(1)3}\dfrac{k_{1}}{k_{2}}\dfrac{\mu_{2}}{\mu_{1}}h_{n}^{(1)}\left(k_{1}R\right) \end{align*} Соотношения между коэффициентами запишем в виде S-матрицы. По аналогии со случаем плоских волн коэффициенты этой матрицы можно трактовать как коэффициенты прохождения и отражения: \begin{equation*} \left( \! \begin{array}{c} a^{(1)1}_{mn} \\ a^{(2)3}_{mn} \end{array} \! \right) = \left( \! \begin{array}{cc} r_{11mn} & t_{12mn} \\ t_{21mn} & r_{22mn} \end{array} \! \right) \left( \! \begin{array}{c} a^{(1)3}_{mn} \\ a^{(2)1}_{mn} \end{array} \! \right) = S^{P}_{mn} \left( \! \begin{array}{c} a^{(1)3}_{mn} \\ a^{(3)1}_{mn} \end{array} \! \right) \end{equation*} и аналогично для коэффициентов $b^{P\sigma}_{mn}$. Для вычисления коэффициентов матрицы в явном виде необходимо воспользоваться соотношением, которое следует из формул Вронскианов сферических функций Бесселя: \begin{equation*} j_{n}(z)\frac{d}{dz}[zh_n^{(1)}(z)] - h_n^{(1)}(z)\frac{d}{dz}[zj_n(z)] = \frac{i}{z} \end{equation*} Таким образом, получается \begin{align*} r_{11mn} =& \dfrac{\dfrac{\mu_{2}}{\mu_{1}}h_{n}^{(1)}\left(k_{2}R\right)\tilde{h}_{n}^{(1)}\left(k_{1}R\right)-h_{n}^{(1)}\left(k_{1}R\right)\tilde{h}_{n}^{(1)}\left(k_{2}R\right)}{j_{n}\left(k_{1}R\right)\tilde{h}_{n}^{(1)}\left(k_{2}R\right)-\dfrac{\mu_{2}}{\mu_{1}}h_{n}^{(1)}\left(k_{2}R\right)\tilde{j}_{n}\left(k_{1}R\right)} \\ t_{12mn} =& \frac{i}{k_{2}R}\dfrac{1}{j_{n}\left(k_{1}R\right)\tilde{h}_{n}^{(1)}\left(k_{2}R\right)-\dfrac{\mu_{2}}{\mu_{1}}h_{n}^{(1)}\left(k_{2}R\right)\tilde{j}_{n}\left(k_{1}R\right)} \\ t_{21mn} =& \dfrac{\mu_{2}}{\mu_{1}}\frac{i}{k_{1}R}\dfrac{1}{j_{n}\left(k_{1}R\right)\tilde{h}_{n}^{(1)}\left(k_{2}R\right)-\dfrac{\mu_{2}}{\mu_{1}}h_{n}^{(1)}\left(k_{2}R\right)\tilde{j}_{n}\left(k_{1}R\right)} \\ r_{22mn} =& \dfrac{\dfrac{\mu_{2}}{\mu_{1}}j_{n}\left(k_{2}R\right)\tilde{j}_{n}\left(k_{1}R\right)-j_{n}\left(k_{1}R\right)\tilde{j}_{n}\left(k_{2}R\right)}{j_{n}\left(k_{1}R\right)\tilde{h}_{n}^{(1)}\left(k_{2}R\right)-\dfrac{\mu_{2}}{\mu_{1}}h_{n}^{(1)}\left(k_{2}R\right)\tilde{j}_{n}\left(k_{1}R\right)} \end{align*} Формулы для второй поляризации аналогичны.

Аналогичные результаты можно получить и для случая цилиндрической геометрии.

Методы S- и Т-матриц¶

Введенные выше матрицы позволяют рассчитывать распространение излучения в слоистых средах, состоящих из однородных слоёв, и средах с пространственно неоднородным распределением материальных параметров. В простейшем случае материальные параметры зависят от координаты $z$ при использовании базиса плоских волн или от расстояния до начала координат $r$ при использовании базиса сферических волн. Тогда матрицы рассеяния и переноса остаются диагональными относительно этого базиса, что существенно упрощает как формулировку методов, так и расчеты.

Для формулировки методов расчета распространения излучения, а именно, когда для заданной внешней падающей волны требуется рассчитать поле излучения во всем пространстве, кроме выведенных выше S- и T-матриц границ разделов сред, нам потребуются соответствующие матрицы, позволяющие связывать амплитуды волн в разных пространственных точках одной и той же однородной изотропной среды. В случае декартовых координат матрица рассеяния такого однородного слоя толщиной $\ell$ должна задавать набег фазы соотетствующих волн на толщине этого слоя: \begin{equation*} S_{\ell} = \left( \! \begin{array}{cc} 0 & \exp{(ik_z\ell)} \\ \exp{(ik_z\ell)} & 0 \end{array} \! \right) \end{equation*}

\begin{equation*} T_{\ell} = \left( \! \begin{array}{cc} \exp{(-ik_z\ell)} & 0 \\ 0 & \exp{(ik_z\ell)} \end{array} \! \right) \end{equation*}

В случае сферической геометрии S-матрица однородного сферического слоя будет представлять собой матрицу с единицами на побочной диагонали, а T-матрица - матрицу с единицами на основной диагонали.

Основным шагом методов является операция композиции двух матриц, $S^{(1,2)}$ или $T^{(1,2)}$, для соседних пространственных областей, например матрицы границы раздела и матрицы однородного слоя. Эта операция позволяет получить матрицу составной области из матриц подобластей этой области. Как следует из определения, для T-матриц такая композиция задается обычным матричным произведением: \begin{equation*} T = T^{(2)} T^{(1))} \end{equation*} Для S-матриц композиция $S = S^{(2)} \ast S^{(1)}$ задается по следующему правилу: \begin{align*} S_{11} =& S^{(1)}_{11} + S^{(1)}_{12} \left( 1-S^{(2)}_{11}S^{(1)}_{22} \right)^{-1} S^{(2)}_{11} S^{(1)}_{21} \\ S_{12} =& S^{(1)}_{12} \left( 1-S^{(2)}_{11}S^{(1)}_{22} \right)^{-1} S^{(2)}_{12} \\ S_{21} =& S^{(2)}_{21} \left( 1-S^{(1)}_{22}S^{(2)}_{11} \right)^{-1} S^{(1)}_{21} \\ S_{22} =& S^{(2)}_{22} + S^{(2)}_{21} \left( 1-S^{(1)}_{22}S^{(2)}_{11} \right)^{-1} S^{(1)}_{22} S^{(2)}_{12} \\ \end{align*} Метод матриц переноса удобен с точки зрения получения аналитических результатов, метод матриц рассеяния является вычислительно устойчивым.

Чтобы рассчитать отражение и прохождение через произвольный неоднородный слой, плоский, сферический или цилиндрический, где задано изменение материальных параметров в соответствующем измерении, нужно разбить его на конечное число тонких по сравнению с длиной волны в матерале подслоев и рассматривать систему как многослойник, состоящий из идущих друг за другом однородных слоев.

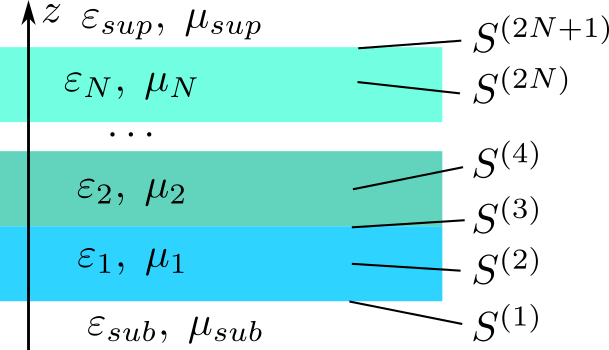
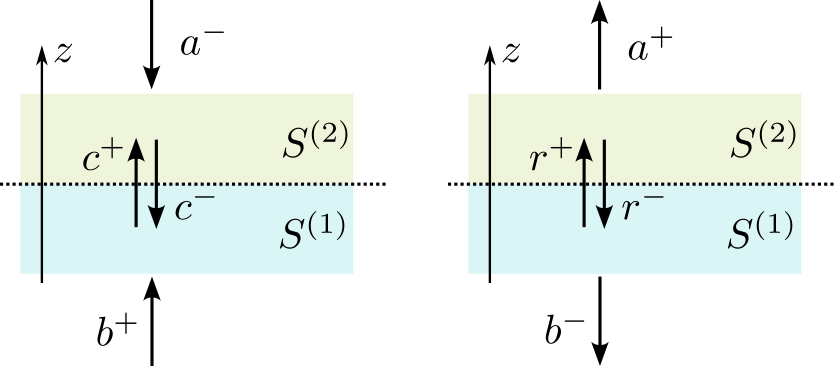
Чтобы найти поле внутри неоднородной структуры с заданной координатой, необходимо рассмотреть две матрицы, $S^{(1,2)}$ или $T^{(1,2)}$, подструктур, граничащих вдоль этой координаты, и по заданным амплитудам падающих на структуру волн внешних источников, расположенных вне структуры, найти амплитуды волн внутри структуры: \begin{equation*} \left( \! \begin{array}{c} c^- \\ c^+ \end{array} \! \right) = \left( \! \begin{array}{cc} \left( 1-S^{(2)}_{11}S^{(1)}_{22} \right)^{-1} S^{(2)}_{11} S^{(1)}_{21} & \left( 1-S^{(2)}_{11}S^{(1)}_{22} \right)^{-1} S^{(2)}_{12} \\ \left( 1-S^{(1)}_{22}S^{(2)}_{11} \right)^{-1} S^{(1)}_{21} & \left( 1-S^{(1)}_{22}S^{(2)}_{11} \right)^{-1} S^{(1)}_{11} S^{(2)}_{12} \end{array} \! \right) \left( \! \begin{array}{c} b^+ \\ a^- \end{array} \! \right) \end{equation*}

Если источник расположен внутри неоднородной структуры, и $S^{(1,2)}$ или $T^{(1,2)}$ - матрицы подструктур, окружающих этот источник, то поле излучения вне структуры можно найти по формулам \begin{equation*} \left( \! \begin{array}{c} b^- \\ a^+ \end{array} \! \right) = \left( \! \begin{array}{cc} S^{(1)}_{12} \left( 1-S^{(2)}_{11}S^{(1)}_{22} \right)^{-1} & S^{(1)}_{12} \left( 1-S^{(2)}_{11}S^{(1)}_{22} \right)^{-1} S^{(2)}_{11} \\ S^{(2)}_{21} \left( 1-S^{(1)}_{22}S^{(2)}_{11} \right)^{-1} S^{(1)}_{22} & S^{(2)}_{21} \left( 1-S^{(1)}_{22}S^{(2)}_{11} \right)^{-1} \end{array} \! \right) \left( \! \begin{array}{c} r^- \\ r^+ \end{array} \! \right) \end{equation*} где $r^{\pm}$ - амплитуды излучения в однородной изотропной среде.

К расчету поля внутри структуры (слева), и расчету излучения источников в структуре (справа)

Плоский волновод¶

Рассмотрим пример плоского волновода - слоя однородного материала $-h/2\leq z\leq h/2$ с диэлектрической проницаемостью $\varepsilon_2$, находящегося между дву полубесконечными обкладками с диэлектрическими проницаемостями $\varepsilon_{1,3}$. Обозначим коэффициенты отражения на нижней и верхней границе слоя для волн, падающих изнутри слоя, как $r_L$ и $r_U$ соответственно. Тогда матрицы рассеяния нижней границы, слоя материала волновода, и верхней границы имеют вид \begin{equation*} S^{(1)} = \left(\begin{array}{cc} -r_{L} & 1+r_{L} \\ 1-r_{L} & r_{L} \end{array}\right), \; S^{(2)} = \left(\begin{array}{cc} 0 & e^{ik_zh} \\ e^{ik_zh} & e^{ik_zh} \end{array}\right), \; S^{(3)}=\left(\begin{array}{cc} r_{U} & 1-r_{U} \\ 1+r_{U} & -r_{U} \end{array}\right) \end{equation*} Их композиция даёт матрицу рассеяния волновода: \begin{equation*} S = \left(\begin{array}{cc} -r_{L} + \dfrac{r_{L}\left(1-r_{L}^{2}\right)e^{2ik_{z}h}}{1-r_{U}r_{L}e^{2ik_{z}h}} & \dfrac{\left(1+r_{L}\right)\left(1-r_{U}\right)e^{ik_{z}h}}{1-r_{U}r_{L}e^{2ik_{z}h}} \\ \dfrac{\left(1+r_{U}\right)\left(1-r_{L}\right)e^{ik_{z}h}}{1-r_{U}r_{L}e^{2ik_{z}h}} & -r_{U}+\dfrac{r_{L}\left(1-r_{U}^{2}\right)e^{2ik_{z}h}}{1-r_{U}r_{L}e^{2ik_{z}h}} \end{array}\right) \end{equation*} где $k_z$ - проекция волнового вектора внутри слоя.

В приложениях рассмотренный слой может выступать и как волноведущая структура, и как резонатор Фабри-Перо. Матрица рассеяния дает единый способ описания слоя, позволяя получить и дискретный, и непрерывный спектры. Пусть на структуру падает поле, задаваемое вектором амплитуд $\boldsymbol{a}_{inc}$, а рассеянное поле задается вектором $\boldsymbol{a}_{sca}$. Запишем связь между ними через обратную матрицу $S^{-1}\boldsymbol{a}_{sca} = \boldsymbol{a}_{inc}$. При нулевой правой части решениями этого уравнения будут являться собственные решения $\boldsymbol{a}_{eig}$, то есть, собственные числа будут определяться полюсами матрицы рассеяния.

Пусть для простоты $r_U = r_L = r$. Из явного вида выведенной выше матрицы получаем условие: \begin{equation*} 1-r^{2}\exp\left(2ik_{z}h\right) = 0 \end{equation*} В случае режима Фабри-Перо длина волны такова, что $|r|<1$, и записав условие на фазы, получается условие резонанса Фабри-Перо: \begin{align*} & \Re e\left\{ k_{z}\right\} h+\arg\left(r\right)=\pi l,\thinspace l\in\mathbb{Z} \\ & \exp\left(-\Im m\left\{ k_{z}\right\} h\right)=\left|r\right| \end{align*} В чисто диэлектрической структуре, где показатель преломления слоя выше показателя преломления обкладок, волноводные моды можно получить учтя, что при полном внутреннем отражении $|r|=1$, поскольку проекция волнового вектора внутри слоя $k_z$ является вещественным числом, в снаружи - чисто мнимым числом $i\kappa_z = i\sqrt{k_x^2-\omega^2\varepsilon_1\mu_1}$. Например, для ТЕ мод \begin{equation*} \dfrac{\mu_{1}k_{z}-i\mu_{2}\chi_{z}}{\mu_{1}k_{z}+i\mu_{2}\chi_{z}}\exp\left(ik_{z}h\right)=\pm1 \end{equation*} Разделяя это уравнение на вещественную и мнимую части, с помощью несложных алгебраических преобразований можно получить обычные дисперсионные уравнения для плоского волновода: \begin{align*} & \dfrac{\mu_{1}}{\mu_{2}}k_{z}\tan\left(\dfrac{k_{z}h}{2}\right) = \sqrt{\omega^{2}\left(\varepsilon_2\mu_2-\varepsilon_{1}\mu_{1}\right)-k_{z}^{2}} \\ & \dfrac{\mu_{1}}{\mu_{2}}k_{z}\cot\left(\dfrac{k_{z}h}{2}\right) = -\sqrt{\omega^{2}\left(\varepsilon_2\mu_2-\varepsilon_{1}\mu_{1}\right)-k_{z}^{2}} \end{align*} Их решения имеют простую графическую визуализацию как пересечения кривых тангенса и арктангенса с дугой окружности.

Задача Коши для коэффициента отражения неоднородного слоя¶

Расчет распространения в неоднородной одномерной структуре можно сформулировать как задачу Коши для некоторого дифференциального уравнения. Чтобы его получить, рассмотрим полученное выражение для матрицы рассения некоторого слоя и устремим толщину слоя к нулю. Пусть стоит задача определения коэффициента отражения как функции координты в толщине неоднородного слоя $r(z)$. Тогда начальным условием будет $r(-h/2)=0$. В уравнении для матрицы рассеяния для тонкого слоя толщиной $\Delta\ll n\lambda$, расположенного в точке с координатой $z$, положим $r_L = -r(z)$, и разложим коэффициент Френеля по малому параметру $\Delta$: \begin{equation*} r_{U}=\dfrac{k_{z}\left(z\right)/\eta\left(z\right)-k_{z}\left(z+\Delta\right)/\eta\left(z+\Delta\right)}{k_{z}\left(z+\Delta\right)/\eta\left(z+\Delta\right)+k_{z}\left(z\right)/\eta\left(z\right)}\approx-\dfrac{\left(k_{z}/\eta\right)'}{2\left(k_{z}/\eta\right)}\Delta \end{equation*} Тогда для коэффициента отражения, задаваемого элементом $S_{22}$, \begin{equation*} r\left(z+\Delta\right)=\dfrac{-r_{U}+r\left(z\right)e^{2ik_{z}\Delta}}{1-r\left(z\right)r_{U}e^{2ik_{z}\Delta}} \approx \left(\dfrac{\left(k_{z}/\eta\right)'}{2\left(k_{z}/\eta\right)}-r^{2}\left(z\right)\dfrac{\left(k_{z}/\eta\right)'}{2\left(k_{z}/\eta\right)}+r\left(z\right)2ik_{z}\right)\Delta+r\left(z\right) \end{equation*} Отсюда при $\Delta\rightarrow0$ получаем искомое дифференциальное уравнение, которое можно решить, например, методом Рунге-Кутта: \begin{equation*} \dfrac{dr}{dz}=2ik_{z}r\left(z\right)+\dfrac{\left(k_{z}/\eta\right)'}{2\left(k_{z}/\eta\right)}\left[1-r^{2}\left(z\right)\right] \end{equation*}

Литература¶

Orfanidis, J. Electromagnetic waves and antennas, Ch. 5-8 Rutgers University (2016)
N. P. K. Cotter, T. W. Preist, and J. R. Sambles, Scattering-matrix approach to multilayer diffraction, J. Opt. Soc. Am. A 12, 1097-1103 (1995)
A.A. Shcherbakov, A.V. Tishchenko, D.S. Setz, B.C. Krummacher, Rigorous S-matrix approach to the modeling of the optical properties of OLEDs, Organic Electronics 12, 4, 654-659 (2011)
J. E. Davis, Multilayer reflectivity (2014)