import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from IPython.display import YouTubeVideo
from scipy.stats import norm
Multidimensional Kalman Filter¶
for a Constant Acceleration Model (CA)¶
Situation covered: You have a Position Sensor (e.g. a Vision System) and try to calculate velocity ($\dot x$ and $\dot y$) as well as position ($x$ and $y$) of a ball in 3D space.
YouTubeVideo("tIIJME8-au8")
State Vector - Constant Acceleration¶
Constant Acceleration Model for Motion in 3D
$$x= \left[ \matrix{ x \\ y \\ z \\ \dot x \\ \dot y \\ \dot z \\ \ddot x \\ \ddot y \\ \ddot z} \right]$$Formal Definition:
$$x_{k+1} = A \cdot x_{k} + B \cdot u_k$$Hence, we have no control input $u$.
$$x_{k+1} = \begin{bmatrix}1 & 0 & 0 & \Delta t & 0 & 0 & \frac{1}{2}\Delta t^2 & 0 & 0 \\ 0 & 1 & 0 & 0 & \Delta t & 0 & 0 & \frac{1}{2}\Delta t^2 & 0 \\ 0 & 0 & 1 & 0 & 0 & \Delta t & 0 & 0 & \frac{1}{2}\Delta t^2 \\ 0 & 0 & 0 & 1 & 0 & 0 & \Delta t & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & \Delta t & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & \Delta t \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ \dot x \\ \dot y \\ \dot z \\ \ddot x \\ \ddot y \\ \ddot z\end{bmatrix}_{k}$$$$y = H \cdot x$$Position ($x$ & $y$ & $z$) is measured with vision system:
$$y = \begin{bmatrix}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \cdot x$$Initial Uncertainty¶
P = 100.0*np.eye(9)
fig = plt.figure(figsize=(6, 6))
im = plt.imshow(P, interpolation="none", cmap=plt.get_cmap('binary'))
plt.title('Initial Covariance Matrix $P$')
ylocs, ylabels = plt.yticks()
# set the locations of the yticks
plt.yticks(np.arange(10))
# set the locations and labels of the yticks
plt.yticks(np.arange(9),('$x$', '$y$', '$z$', '$\dot x$', '$\dot y$', '$\dot z$', '$\ddot x$', '$\ddot y$', '$\ddot z$'), fontsize=22)
xlocs, xlabels = plt.xticks()
# set the locations of the yticks
plt.xticks(np.arange(7))
# set the locations and labels of the yticks
plt.xticks(np.arange(9),('$x$', '$y$', '$z$', '$\dot x$', '$\dot y$', '$\dot z$', '$\ddot x$', '$\ddot y$', '$\ddot z$'), fontsize=22)
plt.xlim([-0.5,8.5])
plt.ylim([8.5, -0.5])
from mpl_toolkits.axes_grid1 import make_axes_locatable
divider = make_axes_locatable(plt.gca())
cax = divider.append_axes("right", "5%", pad="3%")
plt.colorbar(im, cax=cax)
plt.tight_layout()
Dynamic Matrix¶
dt = 0.01 # Time Step between Filter Steps
A = np.matrix([[1.0, 0.0, 0.0, dt, 0.0, 0.0, 1/2.0*dt**2, 0.0, 0.0],
[0.0, 1.0, 0.0, 0.0, dt, 0.0, 0.0, 1/2.0*dt**2, 0.0],
[0.0, 0.0, 1.0, 0.0, 0.0, dt, 0.0, 0.0, 1/2.0*dt**2],
[0.0, 0.0, 0.0, 1.0, 0.0, 0.0, dt, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, dt, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, dt],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0]])
print(A.shape)
(9, 9)
Measurement Matrix¶
Here you can determine, which of the states is covered by a measurement. In this example, the position ($x$ and $y$) is measured.
H = np.matrix([[1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]])
print(H, H.shape)
[[1. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0.]] (3, 9)
Measurement Noise Covariance Matrix $R$¶
rp = 1.0**2 # Noise of Position Measurement
R = np.matrix([[rp, 0.0, 0.0],
[0.0, rp, 0.0],
[0.0, 0.0, rp]])
print(R, R.shape)
fig = plt.figure(figsize=(4, 4))
im = plt.imshow(R, interpolation="none", cmap=plt.get_cmap('binary'))
plt.title('Measurement Noise Covariance Matrix $R$')
ylocs, ylabels = plt.yticks()
# set the locations of the yticks
plt.yticks(np.arange(4))
# set the locations and labels of the yticks
plt.yticks(np.arange(3),('$x$', '$y$', '$z$'), fontsize=22)
xlocs, xlabels = plt.xticks()
# set the locations of the yticks
plt.xticks(np.arange(4))
# set the locations and labels of the yticks
plt.xticks(np.arange(3),('$x$', '$y$', '$z$'), fontsize=22)
plt.xlim([-0.5,2.5])
plt.ylim([2.5, -0.5])
from mpl_toolkits.axes_grid1 import make_axes_locatable
divider = make_axes_locatable(plt.gca())
cax = divider.append_axes("right", "5%", pad="3%")
plt.colorbar(im, cax=cax)
plt.tight_layout()
[[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]] (3, 3)
Process Noise Covariance Matrix $Q$ for CA Model¶
The Position of an object can be influenced by a force (e.g. wind), which leads to an acceleration disturbance (noise). This process noise has to be modeled with the process noise covariance matrix Q.
To easily calcualte Q, one can ask the question: How the noise effects my state vector? For example, how the jerk change the position over one timestep dt. With $\sigma_{j}$ as the magnitude of the standard deviation of the jerk, which distrubs the ball in 3D space. We do not assume cross correlation, which means if a jerk will act in x direction of the movement, it will not push in y or z direction.
We can construct the values with the help of a matrix $G$, which is an "actor" to the state vector.
Symbolic Calculation¶
from sympy import Symbol, Matrix
from sympy.interactive import printing
printing.init_printing()
dts = Symbol('\Delta t')
Gs = Matrix([dts**3/6, dts**2/2, dts])
Gs
Gs*Gs.T
sj = 0.1
Q = np.matrix([[(dt**6)/36, 0, 0, (dt**5)/12, 0, 0, (dt**4)/6, 0, 0],
[0, (dt**6)/36, 0, 0, (dt**5)/12, 0, 0, (dt**4)/6, 0],
[0, 0, (dt**6)/36, 0, 0, (dt**5)/12, 0, 0, (dt**4)/6],
[(dt**5)/12, 0, 0, (dt**4)/4, 0, 0, (dt**3)/2, 0, 0],
[0, (dt**5)/12, 0, 0, (dt**4)/4, 0, 0, (dt**3)/2, 0],
[0, 0, (dt**5)/12, 0, 0, (dt**4)/4, 0, 0, (dt**3)/2],
[(dt**4)/6, 0, 0, (dt**3)/2, 0, 0, (dt**2), 0, 0],
[0, (dt**4)/6, 0, 0, (dt**3)/2, 0, 0, (dt**2), 0],
[0, 0, (dt**4)/6, 0, 0, (dt**3)/2, 0, 0, (dt**2)]]) *sj**2
print(Q.shape)
(9, 9)
fig = plt.figure(figsize=(6, 6))
im = plt.imshow(Q, interpolation="none", cmap=plt.get_cmap('binary'))
plt.title('Process Noise Covariance Matrix $Q$')
ylocs, ylabels = plt.yticks()
# set the locations of the yticks
plt.yticks(np.arange(10))
# set the locations and labels of the yticks
plt.yticks(np.arange(9),('$x$', '$y$', '$z$', '$\dot x$', '$\dot y$', '$\dot z$', '$\ddot x$', '$\ddot y$', '$\ddot z$'), fontsize=22)
xlocs, xlabels = plt.xticks()
# set the locations of the yticks
plt.xticks(np.arange(7))
# set the locations and labels of the yticks
plt.xticks(np.arange(9),('$x$', '$y$', '$z$', '$\dot x$', '$\dot y$', '$\dot z$', '$\ddot x$', '$\ddot y$', '$\ddot z$'), fontsize=22)
plt.xlim([-0.5,8.5])
plt.ylim([8.5, -0.5])
from mpl_toolkits.axes_grid1 import make_axes_locatable
divider = make_axes_locatable(plt.gca())
cax = divider.append_axes("right", "5%", pad="3%")
plt.colorbar(im, cax=cax)
plt.tight_layout()
Disturbance Control Matrix $B$¶
B = np.matrix([[0.0],
[0.0],
[0.0],
[0.0],
[0.0],
[0.0],
[0.0],
[0.0],
[0.0]])
print(B, B.shape)
[[0.] [0.] [0.] [0.] [0.] [0.] [0.] [0.] [0.]] (9, 1)
Control Input $u$¶
Assumed constant over time
u = 0.0
Identity Matrix¶
I = np.eye(9)
print(I, I.shape)
[[1. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 1. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 1. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 1. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 1. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 1. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 1.]] (9, 9)
Measurements¶
Synthetically creation of the Position Data for the ball
Hz = 100.0 # Frequency of Vision System
dt = 1.0/Hz
T = 1.0 # s measuremnt time
m = int(T/dt) # number of measurements
px= 0.0 # x Position Start
py= 0.0 # y Position Start
pz= 1.0 # z Position Start
vx = 10.0 # m/s Velocity at the beginning
vy = 0.0 # m/s Velocity
vz = 0.0 # m/s Velocity
c = 0.1 # Drag Resistance Coefficient
d = 0.9 # Damping
Xr=[]
Yr=[]
Zr=[]
for i in range(int(m)):
accx = -c*vx**2 # Drag Resistance
vx += accx*dt
px += vx*dt
accz = -9.806 + c*vz**2 # Gravitation + Drag
vz += accz*dt
pz += vz*dt
if pz<0.01:
vz=-vz*d
pz+=0.02
if vx<0.1:
accx=0.0
accz=0.0
Xr.append(px)
Yr.append(py)
Zr.append(pz)
Add Noise to the Real Position¶
sp= 0.1 # Sigma for position noise
Xm = Xr + sp * (np.random.randn(m))
Ym = Yr + sp * (np.random.randn(m))
Zm = Zr + sp * (np.random.randn(m))
fig = plt.figure(figsize=(16,9))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(Xm, Ym, Zm, c='gray')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.title('Ball Trajectory observed from Computer Vision System (with Noise)')
#ax.w_xaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
# Axis equal
max_range = np.array([Xm.max()-Xm.min(), Ym.max()-Ym.min(), Zm.max()-Zm.min()]).max() / 3.0
mean_x = Xm.mean()
mean_y = Ym.mean()
mean_z = Zm.mean()
ax.set_xlim(mean_x - max_range, mean_x + max_range)
ax.set_ylim(mean_y - max_range, mean_y + max_range)
ax.set_zlim(mean_z - max_range, mean_z + max_range)
#plt.savefig('BallTrajectory-Computervision.png', dpi=150, bbox_inches='tight')
measurements = np.vstack((Xm,Ym,Zm))
print(measurements.shape)
(3, 100)
Initial State¶
x = np.matrix([0.0, 0.0, 1.0, 10.0, 0.0, 0.0, 0.0, 0.0, -9.81]).T
print(x, x.shape)
[[ 0. ] [ 0. ] [ 1. ] [10. ] [ 0. ] [ 0. ] [ 0. ] [ 0. ] [-9.81]] (9, 1)
# Preallocation for Plotting
xt = []
yt = []
zt = []
dxt= []
dyt= []
dzt= []
ddxt=[]
ddyt=[]
ddzt=[]
Zx = []
Zy = []
Zz = []
Px = []
Py = []
Pz = []
Pdx= []
Pdy= []
Pdz= []
Pddx=[]
Pddy=[]
Pddz=[]
Kx = []
Ky = []
Kz = []
Kdx= []
Kdy= []
Kdz= []
Kddx=[]
Kddy=[]
Kddz=[]
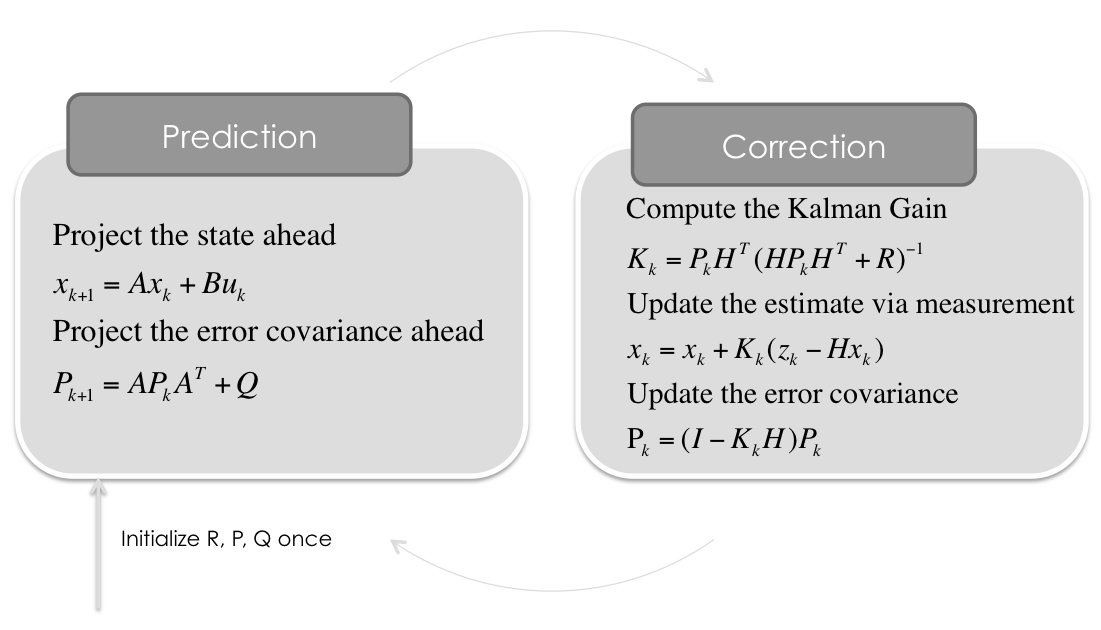
Kalman Filter¶
hitplate=False
for filterstep in range(m):
# Model the direction switch, when hitting the plate
if x[2]<0.01 and not hitplate:
x[5]=-x[5]
hitplate=True
# Time Update (Prediction)
# ========================
# Project the state ahead
x = A*x + B*u
# Project the error covariance ahead
P = A*P*A.T + Q
# Measurement Update (Correction)
# ===============================
# Compute the Kalman Gain
S = H*P*H.T + R
K = (P*H.T) * np.linalg.pinv(S)
# Update the estimate via z
Z = measurements[:,filterstep].reshape(H.shape[0],1)
y = Z - (H*x) # Innovation or Residual
x = x + (K*y)
# Update the error covariance
P = (I - (K*H))*P
# Save states for Plotting
xt.append(float(x[0]))
yt.append(float(x[1]))
zt.append(float(x[2]))
dxt.append(float(x[3]))
dyt.append(float(x[4]))
dzt.append(float(x[5]))
ddxt.append(float(x[6]))
ddyt.append(float(x[7]))
ddzt.append(float(x[8]))
Zx.append(float(Z[0]))
Zy.append(float(Z[1]))
Zz.append(float(Z[2]))
Px.append(float(P[0,0]))
Py.append(float(P[1,1]))
Pz.append(float(P[2,2]))
Pdx.append(float(P[3,3]))
Pdy.append(float(P[4,4]))
Pdz.append(float(P[5,5]))
Pddx.append(float(P[6,6]))
Pddy.append(float(P[7,7]))
Pddz.append(float(P[8,8]))
Kx.append(float(K[0,0]))
Ky.append(float(K[1,0]))
Kz.append(float(K[2,0]))
Kdx.append(float(K[3,0]))
Kdy.append(float(K[4,0]))
Kdz.append(float(K[5,0]))
Kddx.append(float(K[6,0]))
Kddy.append(float(K[7,0]))
Kddz.append(float(K[8,0]))
Plots¶
Estimated State¶
fig = plt.figure(figsize=(16,9))
plt.subplot(211)
plt.title('Estimated State (elements from vector $x$)')
plt.plot(range(len(measurements[0])),dxt, label='$\dot x$')
plt.plot(range(len(measurements[0])),dyt, label='$\dot y$')
plt.plot(range(len(measurements[0])),dzt, label='$\dot z$')
plt.legend(loc='best',prop={'size':22})
plt.subplot(212)
plt.plot(range(len(measurements[0])),ddxt, label='$\ddot x$')
plt.plot(range(len(measurements[0])),ddyt, label='$\ddot y$')
plt.plot(range(len(measurements[0])),ddzt, label='$\ddot z$')
plt.xlabel('Filter Step')
plt.ylabel('')
plt.legend(loc='best',prop={'size':22})
<matplotlib.legend.Legend at 0x1a1740f0f0>
Uncertainty¶
fig = plt.figure(figsize=(16,9))
plt.subplot(311)
plt.plot(range(len(measurements[0])),Px, label='$x$')
plt.plot(range(len(measurements[0])),Py, label='$y$')
plt.plot(range(len(measurements[0])),Pz, label='$z$')
plt.title('Uncertainty (Elements from Matrix $P$)')
plt.legend(loc='best',prop={'size':22})
plt.subplot(312)
plt.plot(range(len(measurements[0])),Pdx, label='$\dot x$')
plt.plot(range(len(measurements[0])),Pdy, label='$\dot y$')
plt.plot(range(len(measurements[0])),Pdz, label='$\dot z$')
plt.legend(loc='best',prop={'size':22})
plt.subplot(313)
plt.plot(range(len(measurements[0])),Pddx, label='$\ddot x$')
plt.plot(range(len(measurements[0])),Pddy, label='$\ddot y$')
plt.plot(range(len(measurements[0])),Pddz, label='$\ddot z$')
plt.xlabel('Filter Step')
plt.ylabel('')
plt.legend(loc='best',prop={'size':22})
<matplotlib.legend.Legend at 0x1a1801d748>
Kalman Gains¶
fig = plt.figure(figsize=(16,9))
plt.plot(range(len(measurements[0])),Kx, label='Kalman Gain for $x$')
plt.plot(range(len(measurements[0])),Ky, label='Kalman Gain for $y$')
plt.plot(range(len(measurements[0])),Kz, label='Kalman Gain for $z$')
plt.plot(range(len(measurements[0])),Kdx, label='Kalman Gain for $\dot x$')
plt.plot(range(len(measurements[0])),Kdy, label='Kalman Gain for $\dot y$')
plt.plot(range(len(measurements[0])),Kdz, label='Kalman Gain for $\dot z$')
plt.plot(range(len(measurements[0])),Kddx, label='Kalman Gain for $\ddot x$')
plt.plot(range(len(measurements[0])),Kddy, label='Kalman Gain for $\ddot y$')
plt.plot(range(len(measurements[0])),Kddz, label='Kalman Gain for $\ddot z$')
plt.xlabel('Filter Step')
plt.ylabel('')
plt.title('Kalman Gain (the lower, the more the measurement fullfill the prediction)')
plt.legend(loc='best',prop={'size':18})
<matplotlib.legend.Legend at 0x1a1836ad68>
Covariance Matrix¶
fig = plt.figure(figsize=(6, 6))
im = plt.imshow(P, interpolation="none", cmap=plt.get_cmap('binary'))
plt.title('Covariance Matrix $P$ (after %i Filtersteps)' % m)
ylocs, ylabels = plt.yticks()
# set the locations of the yticks
plt.yticks(np.arange(10))
# set the locations and labels of the yticks
plt.yticks(np.arange(9),('$x$', '$y$', '$z$', '$\dot x$', '$\dot y$', '$\dot z$', '$\ddot x$', '$\ddot y$', '$\ddot z$'), fontsize=22)
xlocs, xlabels = plt.xticks()
# set the locations of the yticks
plt.xticks(np.arange(7))
# set the locations and labels of the yticks
plt.xticks(np.arange(9),('$x$', '$y$', '$z$', '$\dot x$', '$\dot y$', '$\dot z$', '$\ddot x$', '$\ddot y$', '$\ddot z$'), fontsize=22)
plt.xlim([-0.5,8.5])
plt.ylim([8.5, -0.5])
from mpl_toolkits.axes_grid1 import make_axes_locatable
divider = make_axes_locatable(plt.gca())
cax = divider.append_axes("right", "5%", pad="3%")
plt.colorbar(im, cax=cax)
plt.tight_layout()
Position in x/z Plane¶
fig = plt.figure(figsize=(16,9))
plt.plot(xt,zt, label='Kalman Filter Estimate')
plt.scatter(Xm,Zm, label='Measurement', c='gray', s=30)
plt.plot(Xr, Zr, label='Real')
plt.title('Estimate of Ball Trajectory (Elements from State Vector $x$)')
plt.legend(loc='best',prop={'size':22})
plt.axhline(0, color='k')
plt.axis('equal')
plt.xlabel('X ($m$)')
plt.ylabel('Y ($m$)')
plt.ylim(0, 2);
plt.savefig('Kalman-Filter-CA-Ball-StateEstimated.png', dpi=150, bbox_inches='tight')
Position in 3D¶
fig = plt.figure(figsize=(16,9))
ax = fig.add_subplot(111, projection='3d')
ax.plot(xt,yt,zt, label='Kalman Filter Estimate')
ax.plot(Xr, Yr, Zr, label='Real')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.legend()
plt.title('Ball Trajectory estimated with Kalman Filter')
# Axis equal
max_range = np.array([Xm.max()-Xm.min(), Ym.max()-Ym.min(), Zm.max()-Zm.min()]).max() / 3.0
mean_x = Xm.mean()
mean_y = Ym.mean()
mean_z = Zm.mean()
ax.set_xlim(mean_x - max_range, mean_x + max_range)
ax.set_ylim(mean_y - max_range, mean_y + max_range)
ax.set_zlim(mean_z - max_range, mean_z + max_range)
plt.savefig('Kalman-Filter-CA-Ball-Trajectory.png', dpi=150, bbox_inches='tight')
Conclusion¶
dist = np.sqrt((Xm-xt)**2 + (Ym-yt)**2 + (Zm-zt)**2)
print('Estimated Position is %.2fm away from ball position.' % dist[-1])
Estimated Position is 0.20m away from ball position.
The Kalman Filter is just for linear dynamic systems. The drag resistance coefficient is nonlinear with a state, but the filter can handle this until a certain amount of drag.
But at this time the ball is hitting the ground, the nonlinearity is too much and the filter is providing a wrong solution. Therefore, one have to model a switch in the filter loop, which helps the filter to get it.
Fragen? @Balzer82