PyGBe on Localized Surface Plasmon Resonance (LSPR)¶
Natalia C. Clementi & Lorena A. Barba
The George Washington University, April 2017
PyGBe¶
PyGBe—pronounced _pigbē_—is a Python library that uses the boundary integral method applied to biomolecular electrostatics and (most recently) simple nanoparticle plasmonics.
The official citation for PyGBE is given in Reference 1. The software is shared under the BSD 3-clause license and the development repository is available on Github at https://github.com/barbagroup/pygbe.
The physical model behind PyGBE is an implicit-solvent representation of biomolecules in an ionic solution (i.e., continuum approximation). Interfaces between biomolecules and surroundings (so-called solvent-accessible surfaces) are discretized with triangular elements, where values of electrostatic potential are obtained by collocation. Algorithmically, the solver is accelerated using a treecode; further acceleration on hardware is obtained using GPUs.
The most recent updates to PyGBe allow treating localized surface plasmons quasi-statically. Localized surface plasmon resonance (LSPR) is an optical effect, but electrostatics is a good approximation in the long-wavelength limit. For nanoparticles smaller than the wavelength of incident light, PyGBe can compute the extinction cross-section. We plan to use this new feature of PyGBe to study the suitability and performance of nanobiosensors.
We believe PyGBe to be the first open-source software able to compute extinction cross-sections of arbitrary geometry.
Response of LSPR biosensors¶
LSPR is an optical effect, but electrostatics makes a good approximation in the long-wavelength limit. In this regime, PyGBe's approach can be suitable.
The electric field decays rapidly away from the nanoparticle. Reference 2 shows that analytes are hard to sense if placed further than approximately $15$ nm from the biosensor.
As the sensitivity of LSPR biosensors is highly dependent on distance, we will use PyGBE to study this behavior using a spherical biosensor responding to analytes at different distances.
The boundary integral method used in PyGBe accounts for fine structural details of the analyte and the nanoparticle, as well as the relative position between them.
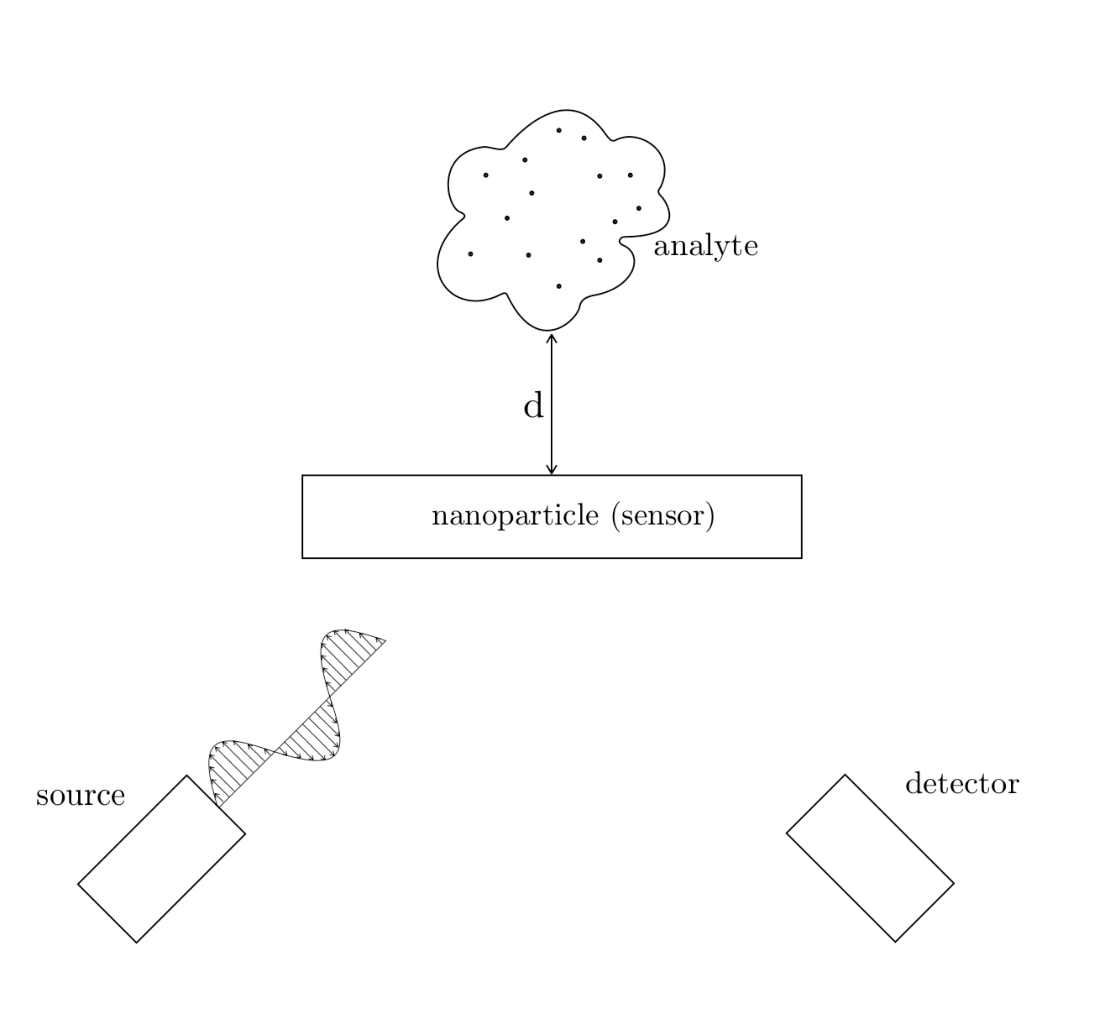
Fig 1. Sketch of an LSPR biosensor from Ref. 3.¶
Scattering in the far field¶
In LSPR computations, we measure the scattered electromagnetic field on a detector that is located far away from the nanoparticle. In the quasistatic approximation, we only need to compute the electric field and the magnetic contribution can be neglected (Ref. 4).
In the far-field limit, the scattered field in the outside region ($\Omega_2$) is given by:
\begin{equation*} \mathbf{E}_{2s} = \frac{1}{4\pi\epsilon_2}k^2\frac{e^{ikr}}{r} (\mathbf{\hat{r}} \times \mathbf{p})\times\mathbf{\hat{r}}. \end{equation*}where $k=2\pi/\lambda$ is the wave number and $\lambda$ the wavelength, $\mathbf{\hat{r}}$ is a unit vector in the direction of the observation point, and $\mathbf{p}$ is the dipole moment.
We can also obtain the scattered field with the forward-scattering amplitude (Ref. 5):
\begin{equation*} \mathbf{E}_{2s}(\mathbf{r})_{r\to\infty} = \frac{e^{ikr}}{r} \mathbf{F}(\mathbf{k},\mathbf{k}_0), \end{equation*}where $\mathbf{F}$ is the forward-scattering amplitude, $\mathbf{k}$ is the scattered wave vector in the direction of propagation, and $\mathbf{k}_0$ the wave vector of the incident field.
Via these two equations, we use PyGBe to compute the scattered electric field and then solve for the forward-scattering amplitude.
Cross extinction section and optical theorem¶
The optical theorem relates the extinction cross-section with the forward-scattering amplitude. The traditional expression for this relationship applies for non-absorbing media (4,5). The expression for absorbing media (Refs. 7 and 8) was recently corrected by Mishchenko (Ref. 9), who gives the following expression:
\begin{equation*} C_\text{ext} = \frac{4\pi}{k^\prime} \operatorname{Im} \left[ \frac{\mathbf{\hat{e}}_i}{|\mathbf{E}_i|}\mathbf{F}(\mathbf{k}=\mathbf{k}_0, \mathbf{k}_0) \right]. \end{equation*}Here, $k^\prime$ is the real part of the complex wave number.
\begin{equation*} k = k^\prime + ik^{\prime\prime} = \frac{2\pi}{\lambda} n, \end{equation*}and $n$ is the refraction index of the host medium.
Preliminary results¶
In the following notebooks, we report on code verification of PyGBe's new LSPR feature using analytical solutions, and grid-convergence analysis.
Analytical solutions for extinction cross-sections are available only for simple spherical geometries. We first compare the results obtained with PyGBe and the analytical solution for isolated spheres. We use four increasingly refined triangular meshes on the spherical surface to study grid convergence. Next, we compute the extinction cross-section as a function of wevelength for silver and gold spheres in water, and compare with the analytical result. See:
The final notebook presents calculations of LSPR response for one spherical nanoparticle surrounded by six spherical "molecules." A grid-convergence study (using Richardson extrapolation) shows that PyGBe is suitable for modeling this phenomenon. See:
References¶
Cooper, C.D., Clementi, N.C., Forsyth, G.F. and Barba, L.A. (2016), PyGBe: Python, GPUs and Boundary elements for biomolecular electrostatics, The Journal of Open Source Software (JOSS), Vol.1(4), doi:10.21105/joss.00043.
Haes, A.J., Zou, S., Schatz, G.C., & Van Duyne, R.P. (2004), A nanoscale optical biosensor: the long range distance dependence of the localized surface plasmon resonance of noble metal nanoparticles, The Journal of Physical Chemistry B Vol.108(1):109-116.
Cooper Villagran, Christopher D. (2015), Biomolecular electrostatics with continuum models: a boundary integral implementation and applications to biosensors, Boston University PhD Thesis. https://open.bu.edu/handle/2144/15650
Mayergoyz, I.D. and Zhang, Z. (2007), The computation of extinction cross sections of resonant metallic nanoparticles subject to optical radiation. IEEE Transactions on Magnetics, Vol.43(4):1681–1684, doi:10.1021/jp0361327.
Jackson, J. D. (1998), Classical Electrodynamics Wiley, 3rd edition.
Bohren, C.F. and Huffman, D.R. (1983), Absorption and Scattering of Light by Small Particles, John Wiley & Sons.
Bohren, C.F. and Gilra, D.P. (1979). Extinction by a spherical particle in an absorbing medium, Journal of Colloid and Interface Science, Vol.72(2):215–221 doi:10.1016/0021-9797(79)90103-6.
Videen, G. and Sun, W. (2003), Yet another look at light scattering from particles in absorbing media, Applied Optics, Vol.42(33):6724–6727 doi:10.1364/AO.42.006724.
Mishchenko, M. I. (2007). Electromagnetic scattering by a fixed finite object embedded in an absorbing medium, Optics Express, Vol.20(15):13188–13202 doi:10.1364/OE.15.013188.
#Ignore this cell, It simply loads a style for the notebook.
from IPython.core.display import HTML
def css_styling():
try:
styles = open("styles/custom.css", "r").read()
return HTML(styles)
except:
pass
css_styling()