Dynamic Models¶

Preliminaries¶

• Goal
  • Introduction to dynamic (=temporal) Latent Variable Models, including the Hidden Markov Model and Kalman filter.
• Materials
  • Mandatory
    • These lecture notes
  • Optional
    • Bishop pp.605-615 on Hidden Markov Models
    • Bishop pp.635-641 on Kalman filters
    • Faragher (2012), Understanding the Basis of the Kalman Filter
    • Minka (1999), From Hidden Markov Models to Linear Dynamical Systems

Example Problem¶

• We consider a one-dimensional cart position tracking problem, see Faragher 2012.

• The hidden states are the position $z_t$ and velocity $\dot z_t$. We can apply an external acceleration/breaking force $u_t$. (Noisy) observations are represented by $x_t$.

• The equations of motions are given by

$$\begin{align*} \begin{bmatrix} z_t \\ \dot{z_t}\end{bmatrix} &= \begin{bmatrix} 1 & \Delta t \\ 0 & 1\end{bmatrix} \begin{bmatrix} z_{t-1} \\ \dot z_{t-1}\end{bmatrix} + \begin{bmatrix} (\Delta t)^2/2 \\ \Delta t\end{bmatrix} u_t + \mathcal{N}(0,\Sigma_z) \\ x_t &= \begin{bmatrix} z_t \\ \dot{z_t}\end{bmatrix} + \mathcal{N}(0,\Sigma_x) \end{align*}$$

• Task: Infer the position $z_t$ after 10 time steps. (Solution later in this lesson).

Dynamical Models¶

• In this lesson, we consider models where the sequence order of observations matters.

• Consider the ordered observation sequence $x^T \triangleq \left(x_1,x_2,\ldots,x_T\right)$.

  • (For brevity, in this lesson we use the notation $x_t^T$ to denote $(x_t,x_{t+1},\ldots,x_T)$ and drop the subscript if $t=1$, so $x^T = x_1^T = \left(x_1,x_2,\ldots,x_T\right)$).

• We wish to develop a generative model $$ p( x^T )$$

that 'explains' the time series $x^T$.

• We cannot use the IID assumption $p( x^T ) = \prod_t p(x_t )$. In general, we can use the chain rule (a.k.a. the general product rule)

$$\begin{align*} p(x^T) &= p(x_T|x^{T-1}) \,p(x^{T-1}) \\ &= p(x_T|x^{T-1}) \,p(x_{T-1}|x^{T-2}) \cdots p(x_2|x_1)\,p(x_1) \\ &= p(x_1)\prod_{t=2}^T p(x_t\,|\,x^{t-1}) \end{align*}$$

• Generally, we will want to limit the depth of dependencies on previous observations. For example, a $K$th-order linear Auto-Regressive (AR) model that is given by

$$\begin{align*} p(x_t\,|\,x^{t-1}) = \mathcal{N}\left(x_t \,\middle|\, \sum_{k=1}^K a_k x_{t-k}\,,\sigma^2\,\right) \end{align*}$$

limits the dependencies to the past $K$ samples.

State-space Models¶

• A limitation of AR models is that they need a lot of parameters in order to create a flexible model. E.g., if $x_t \in \mathbb{R}^M$ is an $M$-dimensional time series, then the $K$-th order AR model for $x_t$ will have $KM^2$ parameters.

• Similar to our work on Gaussian Mixture models, we can create a flexible dynamic system by introducing latent (unobserved) variables $z^T \triangleq \left(z_1,z_2,\dots,z_T\right)$ (one $z_t$ for each observation $x_t$). In dynamic systems, $z_t$ are called state variables.

• A state space model is a particular latent variable dynamical model defined by

$$\begin{align*} p(x^T,z^T) &= \underbrace{p(z_1)}_{\text{initial state}} \prod_{t=2}^T \underbrace{p(z_t\,|\,z_{t-1})}_{\text{state transitions}}\,\prod_{t=1}^T \underbrace{p(x_t\,|\,z_t)}_{\text{observations}} \end{align*}$$

• The condition $p(z_t\,|\,z^{t-1}) = p(z_t\,|\,z_{t-1})$ is called a $1$st-order Markov condition.

• The Forney-style factor graph for a state-space model:

Hidden Markov Models and Linear Dynamical Systems¶

• A Hidden Markov Model (HMM) is a specific state-space model with discrete-valued state variables $z_t$.

• Typically, $z_t$ is a $K$-dimensional one-hot coded latent 'class indicator' with transition probabilities $a_{jk} \triangleq p(z_{tk}=1\,|\,z_{t-1,j}=1)$, or equivalently, $$p(z_t|z_{t-1}) = \prod_{k=1}^K \prod_{j=1}^K a_{jk}^{z_{t-1,j}\cdot z_{tk}}$$

which is usually accompanied by an initial state distribution $p(z_{1k}=1) = \pi_k$.

• The classical HMM has also discrete-valued observations but in pratice any (probabilistic) observation model $p(x_t|z_t)$ may be coupled to the hidden Markov chain.

• Another well-known state-space model with continuous-valued state variables $z_t$ is the (Linear) Gaussian Dynamical System (LGDS), which is defined as

$$\begin{align*} p(z_t\,|\,z_{t-1}) &= \mathcal{N}\left(\, A z_{t-1}\,,\,\Sigma_z\,\right) \\ p(x_t\,|\,z_t) &= \mathcal{N}\left(\, C z_t\,,\,\Sigma_x\,\right) \\ p(z_1) &= \mathcal{N}\left(\, \mu_1\,,\,\Sigma_1\,\right) \end{align*}$$

• Note that the joint distribution over all states and observations $\{(x_1,z_1),\ldots,(x_t,z_t)\}$ is a (large-dimensional) Gaussian distribution. This means that, in principle, every inference problem on the LGDS model also leads to a Gaussian distribution.

• HMM's and LGDS's (and variants thereof) are at the basis of a wide range of complex information processing systems, such as speech and language recognition, robotics and automatic car navigation, and even processing of DNA sequences.

Common Signal Processing Tasks as Message Passing-based Inference¶

• As we have seen, inference tasks in linear Gaussian state space models can be analytically solved.

• However, these derivations quickly become cumbersome and prone to errors.

• Alternatively, we could specify the generative model in a (Forney-style) factor graph and use automated message passing to infer the posterior over the hidden variables. Here follows some examples.

• Filtering, a.k.a. state estimation: estimation of a state (at time step $t$), based on past and current (at $t$) observations.

• Smoothing: estimation of a state based on both past and future observations. Needs backward messages from the future.

• Prediction: estimation of future state or observation based only on observations of the past.

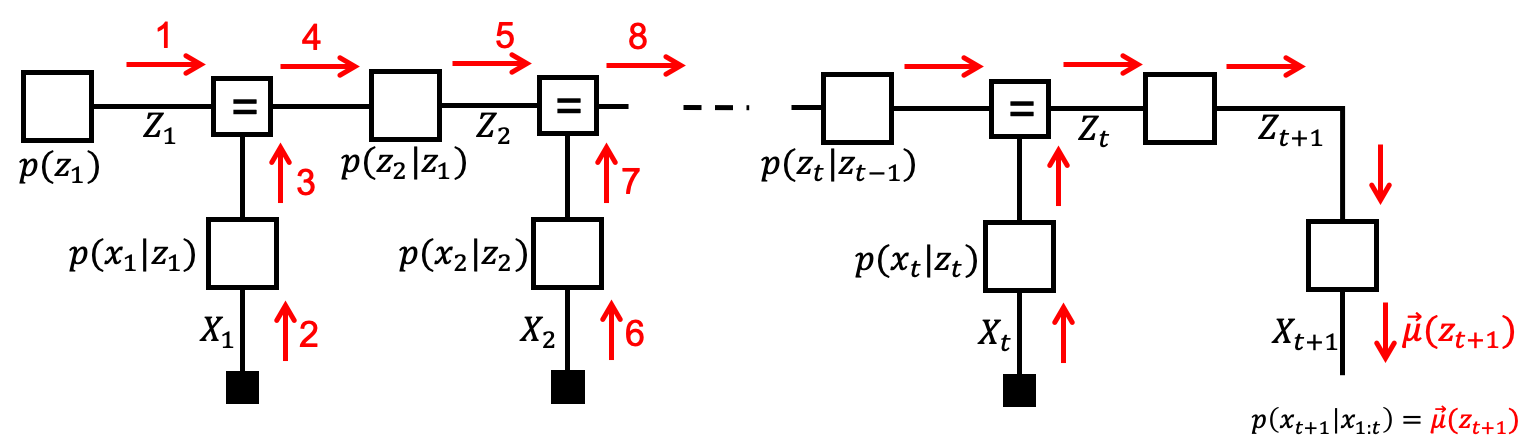
Kalman Filtering¶

• Technically, a Kalman filter is the solution to the recursive estimation (inference) of the hidden state $z_t$ based on past observations in an LGDS, i.e., Kalman filtering solves the problem $p(z_t\,|\,x^t)$ based on the previous estimate $p(z_{t-1}\,|\,x^{t-1})$ and a new observation $x_t$ (in the context of the given model specification of course).

• Let's infer the Kalman filter for a scalar linear Gaussian dynamical system:

$$\begin{aligned} p(z_t\,|\,z_{t-1}) &= \mathcal{N}(z_t\,|\,a z_{t-1},\sigma_z^2) \qquad &&\text{(state transition)} \\ p(x_t\,|\,z_t) &= \mathcal{N}(x_t\,|\,c z_t,\sigma_x^2) \qquad &&\text{(observation)} \end{aligned}$$

• Kalman filtering comprises inferring $p(z_t\,|\,x^t)$ from a given prior estimate $p(z_{t-1}\,|\,x^{t-1})$ (available after the previous time step) and a new observation $x_t$. Let us assume that

$$\begin{align*} p(z_{t-1}\,|\,x^{t-1}) = \mathcal{N}(z_{t-1} \,|\, \mu_{t-1}, \sigma_{t-1}^2) \qquad \text{(prior)} \end{align*}$$

• Note that everything is Gaussian, so it is in principle possible to execute inference problems analytically and the result will be a Gaussian posterior:
  • (In the following derivation we make use of the renormalization equality $\mathcal{N}(x\,|\,cz,\sigma^2) = \frac{1}{c}\mathcal{N}\left(z \,\big|\,\frac{x}{c},\left(\frac{\sigma}{c}\right)^2\right)$).

$$\begin{align*} \underbrace{p(z_t\,|\,x^t)}_{\text{posterior}} &= p(z_t\,|\,x_t,x^{t-1}) \\ &\propto p(x_t,z_t\,|\,x^{t-1}) \\ &= p(x_t\,|\,z_t) \,p(z_t\,|\,x^{t-1}) \\ &= p(x_t\,|\,z_t) \, \int p(z_t,z_{t-1}\,|\,x^{t-1}) \mathrm{d}z_{t-1} \\ &= \underbrace{p(x_t\,|\,z_t)}_{\text{observation}} \, \int \underbrace{p(z_t\,|\,z_{t-1})}_{\text{state transition}} \, \underbrace{p(z_{t-1}\,|\,x^{t-1})}_{\text{prior}} \mathrm{d}z_{t-1} \\ &= \mathcal{N}(x_t\,|\,c z_t,\sigma_x^2) \int \mathcal{N}(z_t\,|\,a z_{t-1},\sigma_z^2) \, \mathcal{N}(z_{t-1} \,|\, \mu_{t-1}, \sigma_{t-1}^2) \mathrm{d}z_{t-1} \\ &= \frac{1}{c}\mathcal{N}\left(z_t\bigm| \frac{x_t}{c} ,\left(\frac{\sigma_x}{c}\right)^2\right) \int \frac{1}{a}\underbrace{\mathcal{N}\left(z_{t-1}\bigm| \frac{z_t}{a},\left(\frac{\sigma_z}{a}\right)^2 \right) \, \mathcal{N}(z_{t-1} \,|\, \mu_{t-1}, \sigma_{t-1}^2)}_{\text{use Gaussian multiplication formula SRG-6}} \mathrm{d}z_{t-1} \\ &\propto \underbrace{\mathcal{N}\left(z_t\,\bigm| \,\frac{x_t}{c} ,\left(\frac{\sigma_x}{c}\right)^2\right) \cdot \mathcal{N}\left(z_t\, \bigm|\,a \mu_{t-1},\sigma_z^2 + \left(a \sigma_{t-1}\right)^2 \right)}_{\text{use SRG-6 again}} \\ &\propto \mathcal{N}\left( z_t \,|\, \mu_t, \sigma_t^2\right) \end{align*}$$

with $$\begin{align*} \rho_t^2 &= a^2 \sigma_{t-1}^2 + \sigma_z^2 \quad \text{(predicted variance)}\\ K_t &= \frac{c \rho_t^2}{c^2 \rho_t^2 + \sigma_x^2} \quad \text{(Kalman gain)} \\ \mu_t &= \underbrace{a \mu_{t-1}}_{\text{prior prediction}} + K_t \cdot \underbrace{\left( x_t - c a \mu_{t-1}\right)}_{\text{prediction error}} \quad \text{(posterior mean)}\\ \sigma_t^2 &= \left( 1 - c\cdot K_t \right) \rho_t^2 \quad \text{(posterior variance)} \end{align*}$$

• Kalman filtering consists of computing/updating these last four equations for each new observation ($x_t$). This is a very efficient recursive algorithm to estimate the state $z_t$ from all observations (until $t$).

• It turns out that it's also possible to get an analytical result for $p(x_t|x^{t-1})$, which is the model evidence in a filtering context. See optional slides for details.

Multi-dimensional Kalman Filtering¶

• The Kalman filter equations can also be derived for multidimensional state-space models. In particular, for the model

$$\begin{align*} z_t &= A z_{t-1} + \mathcal{N}(0,\Gamma) \\ x_t &= C z_t + \mathcal{N}(0,\Sigma) \end{align*}$$

the Kalman filter update equations for the posterior $p(z_t |x^t) = \mathcal{N}\left(z_t \bigm| \mu_t, V_t \right)$ are given by (see Bishop, pg.639) $$\begin{align*} P_t &= A V_{t-1} A^T + \Gamma \qquad &&\text{(predicted variance)}\\ K_t &= P_t C^T \cdot \left(C P_t C^T + \Sigma \right)^{-1} \qquad &&\text{(Kalman gain)} \\ \mu_t &= A \mu_{t-1} + K_t\cdot\left(x_t - C A \mu_{t-1} \right) \qquad &&\text{(posterior state mean)}\\ V_t &= \left(I-K_t C \right) P_{t} \qquad &&\text{(posterior state variance)} \end{align*}$$

Code Example: Kalman Filtering and the Cart Position Tracking Example Revisited¶

• We can now solve the cart tracking problem of the introductory example by implementing the Kalman filter.

The Cart Tracking Problem Revisited: Inference by Message Passing¶

• Let's solve the cart tracking problem by sum-product message passing in a factor graph like the one depicted above. All we have to do is create factor nodes for the state-transition model $p(z_t|z_{t-1})$ and the observation model $p(x_t|z_t)$. Then we let RxInfer execute the message passing schedule.

Now that we've built the model, we can perform Kalman filtering by inserting measurement data into the model and performing message passing.

• Note that both the analytical Kalman filtering solution and the message passing solution lead to the same results. The advantage of message passing-based inference with RxInfer is that we did not need to derive any inference equations. RxInfer took care of all that.

Recap Dynamical Models¶

• Dynamical systems do not obey the sample-by-sample independence assumption, but still can be specified, and state and parameter estimation equations can be solved by similar tools as for static models.

• Two of the more famous and powerful models with latent states include the hidden Markov model (with discrete states) and the Linear Gaussian dynamical system (with continuous states).

• For the LGDS, the Kalman filter is a well-known recursive state estimation procedure. The Kalman filter can be derived through Bayesian update rules on Gaussian distributions.

• If anything changes in the model, e.g., the state noise is not Gaussian, then you have to re-derive the inference equations again from scratch and it may not lead to an analytically pleasing answer.

• $\Rightarrow$ Generally, we will want to automate the inference processes. As we discussed, message passing in a factor graph is a visually appealing method to automate inference processes. We showed how Kalman filtering emerged naturally by automated message passing.

OPTIONAL SLIDES¶

Proof of Kalman filtering equations including evidence updating¶

• Now let's proof the Kalman filtering equations including evidence updating by probabilistic calculus:

$$\begin{align*} \overbrace{p(z_t\,|\,x^t)}^{\text{posterior}} \cdot \overbrace{p(x_t\,|\,x^{t-1})}^{\text{evidence}} &= p(x_t,z_t\,|\,x^{t-1}) \\ &= p(x_t\,|\,z_t) \,p(z_t\,|\,x^{t-1}) \\ &= p(x_t\,|\,z_t) \, \int p(z_t,z_{t-1}\,|\,x^{t-1}) \mathrm{d}z_{t-1} \\ &= p(x_t\,|\,z_t) \, \int p(z_t\,|\,z_{t-1}) \, p(z_{t-1}\,|\,x^{t-1}) \mathrm{d}z_{t-1} \\ &= \underbrace{\mathcal{N}(x_t|c z_t, \sigma_x^2)}_{\text{likelihood}} \, \int \underbrace{\mathcal{N}(z_t\,|\,a z_{t-1},\sigma_z^2)}_{\text{state transition} } \, \underbrace{\mathcal{N}(z_{t-1} \,|\, \mu_{t-1}, \sigma_{t-1}^2) }_{\text{prior}} \mathrm{d}z_{t-1} \end{align*}$$

• The RHS can be further evaluated by making use of the Gaussian multiplication rules and the following renormalization equality:

$$\begin{align*} \mathcal{N}(x\,|\,cz,\sigma^2) = \frac{1}{c}\cdot \mathcal{N}\left(z \,\big|\,\frac{x}{c},\left(\frac{\sigma}{c}\right)^2\right) \qquad &&\text{(renormalization)}\,. \end{align*}$$

In particular, the RHS evaluates to $$\begin{align*} \mathcal{N}(x_t|c z_t, &\sigma_x^2) \, \int \underbrace{\mathcal{N}(z_t\,|\,a z_{t-1},\sigma_z^2)}_{\text{use renormalization}} \mathcal{N}(z_{t-1} \,|\, \mu_{t-1}, \sigma_{t-1}^2) \mathrm{d}z_{t-1} \\ &= \mathcal{N}(x_t|c z_t, \sigma_x^2) \, \int \frac{1}{a}\underbrace{\mathcal{N}\left(z_{t-1}\bigm| \frac{z_t}{a},\left(\frac{\sigma_z}{a}\right)^2 \right) \mathcal{N}(z_{t-1} \,|\, \mu_{t-1}, \sigma_{t-1}^2)}_{\text{use Gaussian multiplication formula SRG-6}} \mathrm{d}z_{t-1} \\ &= \frac{1}{a} \mathcal{N}(x_t|c z_t, \sigma_x^2) \, \int \underbrace{\mathcal{N}\left(\mu_{t-1}\bigm| \frac{z_t}{a},\left(\frac{\sigma_z}{a}\right)^2 + \sigma_{t-1}^2 \right)}_{\text{not a function of }z_{t-1}} \underbrace{\mathcal{N}(z_{t-1} \,|\, \cdot, \cdot)}_{\text{integrates to }1} \mathrm{d}z_{t-1} \\ &= \frac{1}{a} \underbrace{\mathcal{N}(x_t|c z_t, \sigma_x^2)}_{\text{use renormalization rule}} \, \underbrace{\mathcal{N}\left(\mu_{t-1}\bigm| \frac{z_t}{a},\left(\frac{\sigma_z}{a}\right)^2 + \sigma_{t-1}^2 \right)}_{\text{use renormalization rule}} \\ &= \frac{1}{c} \underbrace{\mathcal{N}\left(z_t \bigm| \frac{x_t}{c}, \left( \frac{\sigma_x}{c}\right)^2 \right) \mathcal{N}\left(z_t\, \bigm|\,a \mu_{t-1},\sigma_z^2 + \left(a \sigma_{t-1}\right)^2 \right)}_{\text{use SRG-6 again}} \\ &= \underbrace{\frac{1}{c} \mathcal{N}\left( \frac{x_t}{c} \bigm| a \mu_{t-1}, \left( \frac{\sigma_x}{c}\right)^2+ \sigma_z^2 + \left(a \sigma_{t-1}\right)^2\right)}_{\text{use renormalization}} \, \mathcal{N}\left( z_t \,|\, \mu_t, \sigma_t^2\right)\\ &= \underbrace{\mathcal{N}\left(x_t \,|\, ca \mu_{t-1}, \sigma_x^2 + c^2(\sigma_z^2+a^2\sigma_{t-1}^2) \right)}_{\text{evidence } p(x_t|x^{t-1})} \cdot \underbrace{\mathcal{N}\left( z_t \,|\, \mu_t, \sigma_t^2\right)}_{\text{posterior }p(z_t|x^t) } \end{align*}$$ with $$\begin{align*} \rho_t^2 &= a^2 \sigma_{t-1}^2 + \sigma_z^2 \qquad &&\text{(predicted variance)}\\ K_t &= \frac{c \rho_t^2}{c^2 \rho_t^2 + \sigma_x^2} \qquad &&\text{(Kalman gain)} \\ \mu_t &= \underbrace{a \mu_{t-1}}_{\text{prior prediction}} + K_t \cdot \underbrace{\left( x_t - c a \mu_{t-1}\right)}_{\text{prediction error}} \qquad &&\text{(posterior mean)}\\ \sigma_t^2 &= \left( 1 - c\cdot K_t \right) \rho_t^2 \qquad &&\text{(posterior variance)} \end{align*}$$

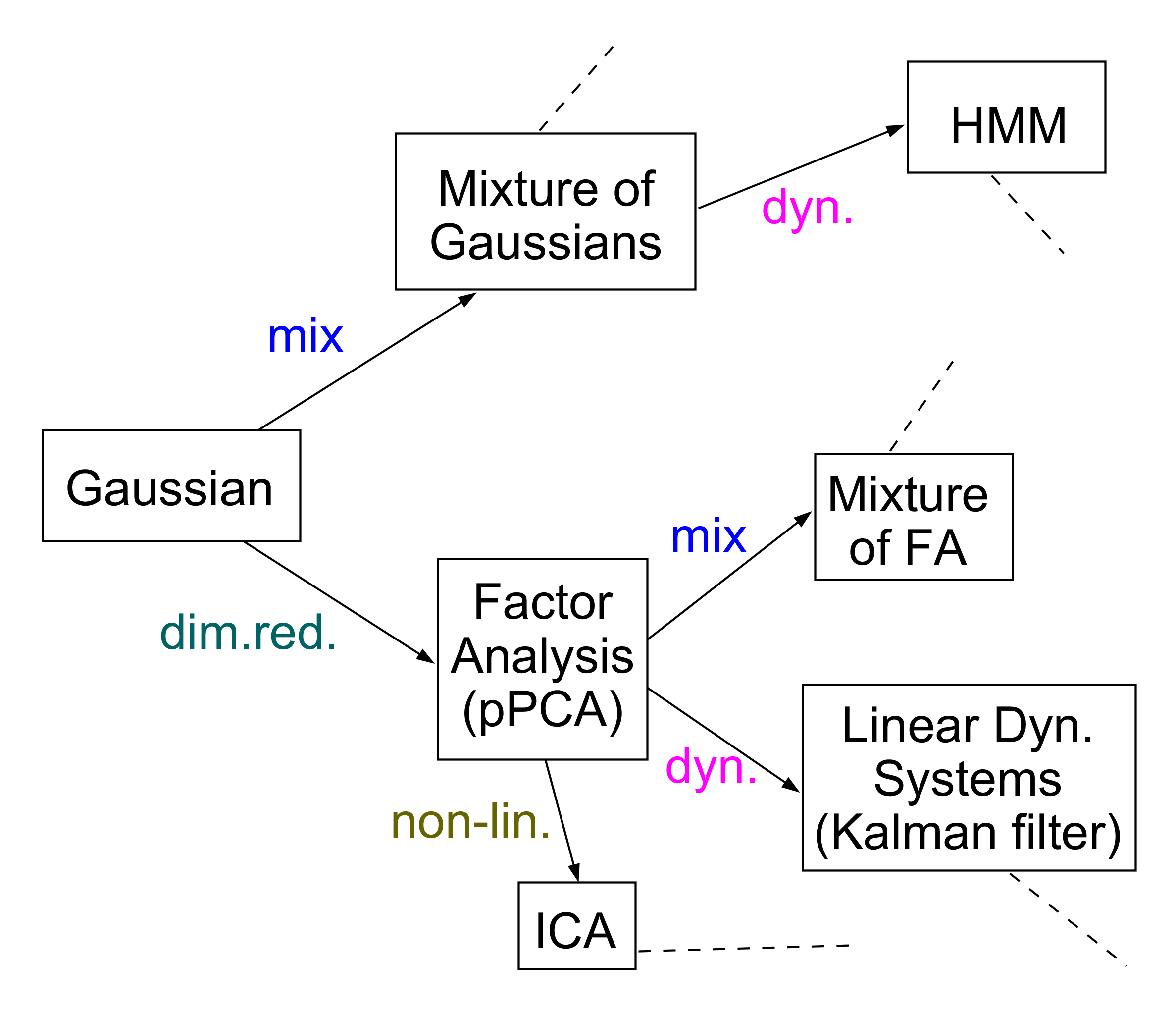
Extensions of Generative Gaussian Models¶

• Using the methods of the previous lessons, it is possible to create your own new models based on stacking Gaussian and categorical distributions in new ways: