Factor Graphs¶
- [1] Consider the following state-space model:
where $k=1,2,\ldots,n$ is the time step counter; $z_k$ is an unobserved state sequence; $x_k$ is an observed sequence; $w_k \sim \mathcal{N}(0,\Sigma_w)$ and $v_k \sim \mathcal{N}(0,\Sigma_v)$ are (unobserved) state and observation noise sequences respectively; $z_0 \sim \mathcal{N}(0,\Sigma_0)$ is the initial state and $A$, $C$, $\Sigma_v$,$\Sigma_w$ and $\Sigma_0$ are known parameters. The Forney-style factor graph (FFG) for one time step is depicted here:
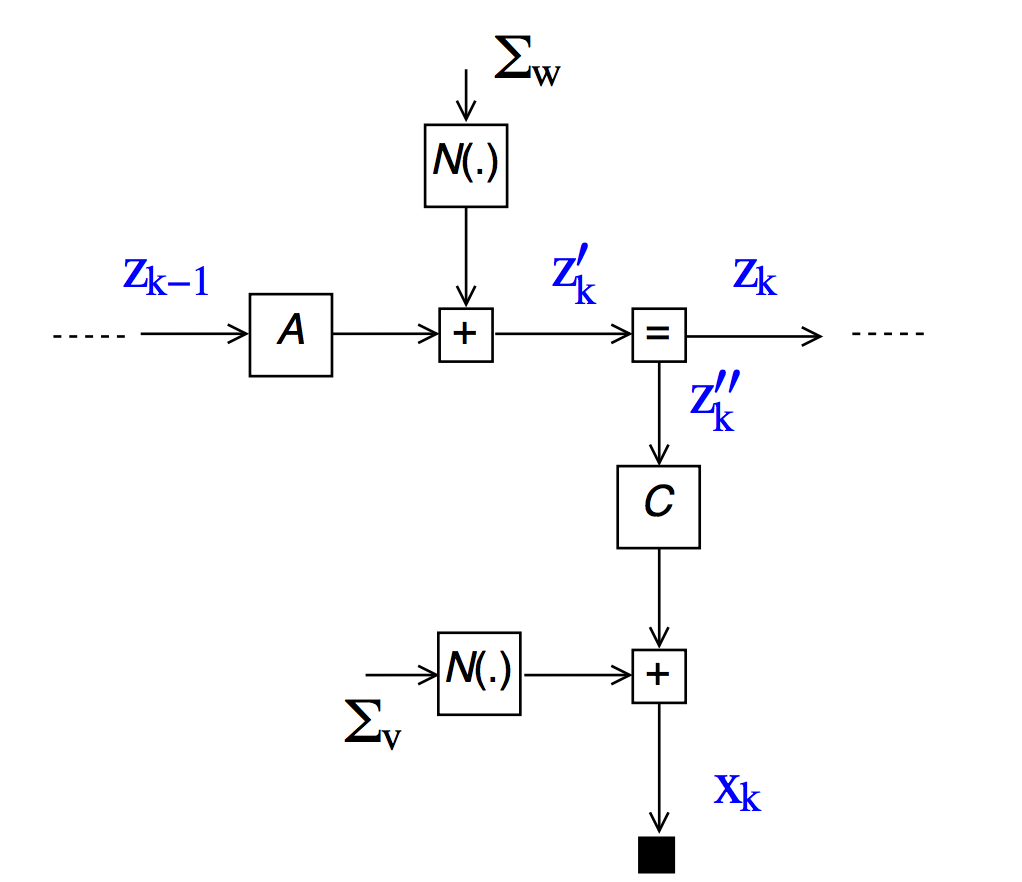 (a) Rewrite the state-space equations as a set of conditional probability distributions.
$$\begin{align*}
p(z_k|z_{k-1},A,\Sigma_w) &= \ldots \\
p(x_k|z_k,C,\Sigma_v) &= \ldots \\
p(z_0|\Sigma_0) &= \ldots
\end{align*}$$
(b) Define $z^n \triangleq (z_0,z_1,\ldots,z_n)$, $x^n \triangleq (x_1,\ldots,x_n)$ and $\theta=\{A,C,\Sigma_w,\Sigma_v\}$. Now write out the generative model $p(x^n,z^n|\theta)$ as a product of factors.
(c) We are interested in estimating $z_k$ from a given estimate for $z_{k-1}$ and the current observation $x_k$, i.e., we are interested in computing $p(z_k|z_{k-1},x_k,\theta)$. Can $p(z_k|z_{k-1},x_k,\theta)$ be expressed as a Gaussian distribution? Explain why or why not in one sentence.
(d) Copy the graph onto your exam paper and draw the message passing schedule for computing $p(z_k|z_{k-1},x_k,\theta)$ by drawing arrows in the factor graph. Indicate the order of the messages by assigning numbers to the arrows.
(e) Now assume that our belief about parameter $\Sigma_v$ is instead given by a distribution $p(\Sigma_v)$ (rather than a known value). Adapt the factor graph drawing of the previous answer to reflects our belief about $\Sigma_v$.
(a) Rewrite the state-space equations as a set of conditional probability distributions.
$$\begin{align*}
p(z_k|z_{k-1},A,\Sigma_w) &= \ldots \\
p(x_k|z_k,C,\Sigma_v) &= \ldots \\
p(z_0|\Sigma_0) &= \ldots
\end{align*}$$
(b) Define $z^n \triangleq (z_0,z_1,\ldots,z_n)$, $x^n \triangleq (x_1,\ldots,x_n)$ and $\theta=\{A,C,\Sigma_w,\Sigma_v\}$. Now write out the generative model $p(x^n,z^n|\theta)$ as a product of factors.
(c) We are interested in estimating $z_k$ from a given estimate for $z_{k-1}$ and the current observation $x_k$, i.e., we are interested in computing $p(z_k|z_{k-1},x_k,\theta)$. Can $p(z_k|z_{k-1},x_k,\theta)$ be expressed as a Gaussian distribution? Explain why or why not in one sentence.
(d) Copy the graph onto your exam paper and draw the message passing schedule for computing $p(z_k|z_{k-1},x_k,\theta)$ by drawing arrows in the factor graph. Indicate the order of the messages by assigning numbers to the arrows.
(e) Now assume that our belief about parameter $\Sigma_v$ is instead given by a distribution $p(\Sigma_v)$ (rather than a known value). Adapt the factor graph drawing of the previous answer to reflects our belief about $\Sigma_v$.
- [2] Consider an addition node $$f_+(x,y,z) = \delta(z-x-y)$$
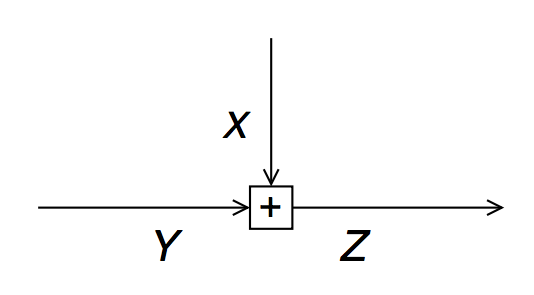
(a) Derive an expression for the outgoing message $\overrightarrow{\mu}_{Z}(z)$ in terms of the incoming messages $\overrightarrow{\mu}_{X}(\cdot)$ and $\overrightarrow{\mu}_{Y}(\cdot)$.
(b) Now assume that both incoming messages are Gaussian, namely $\overrightarrow{\mu}_{X}(x) \sim \mathcal{N}(\overrightarrow{m}_X,\overrightarrow{V}_X)$ and $\overrightarrow{\mu}_{Y}(y) \sim \mathcal{N}(\overrightarrow{m}_Y,\overrightarrow{V}_Y)$. Evaluate the outgoing message $\overrightarrow{\mu}_{Z}(z)$. You will need the multiplication rule for Gaussians.
(c) For the same summation node, work out the SP update rule for the backward message $\overleftarrow{\mu}_{X}(x)$ as a function of $\overrightarrow{\mu}_{Y}(y)$ and $\overleftarrow{\mu}_{Z}(z)$. And further refine the answer for Gaussian messages.