The General EM Algorithm¶
Preliminaries¶
- Goal
- A more formal treatment of the general EM algorithm
- Materials
- Mandatory
- These lecture notes
- Optional
- Bishop pp. 55-57 for Jensen's inequality
- Bishop pp. 439-443 for EM applied to GMM
- Bishop pp. 450-455 for the general EM algorithm
- Liang (2015) Technical Details about the EM algorithm
- Bo and Batzoglou (2008) What is the expectation algorithm?
- Mandatory
The Kullback-Leibler Divergence¶
In order to prove that the EM algorithm works, we will need Gibbs inequality, which is a famous theorem in information theory.
Definition: the Kullback-Leibler divergence (a.k.a. relative entropy) is a distance measure between two distributions $q$ and $p$ and is defined as
- Theorem: Gibbs Inequality (proof uses Jensen inquality):
with equality only iff $p=q$.
- Note that the KL divergence is an asymmetric distance measure, i.e. in general
EM by maximizing a Lower Bound on the Log-Likelihood¶
- Consider a model for observations $x$, hidden variables $z$ and tuning parameters $\theta$. Note that, for any distribution $q(z)$, we can expand the log-likelihood as follows:
- Hence, $\mathrm{LB}(q,\theta)$ is a lower bound on the log-likelihood $\log p(x|\theta)$.
- Technically, the Expectation-Maximization (EM) algorithm is defined by coordinate ascent on $\mathrm{LB}(q,\theta)$:
- Since $\mathrm{LB}(q,\theta) \leq \mathrm{L}(\theta)$ (for all choices of $q(z)$), maximizing the lower-bound $\mathrm{LB}$ will also maximize the log-likelihood wrt $\theta$. The reason to maximize $\mathrm{LB}$ rather than log-likelihood $\mathrm{L}$ directly is that $\arg\max \mathrm{LB}$ often leads to easier expressions. E.g., see this illustrative figure (Bishop p.453):
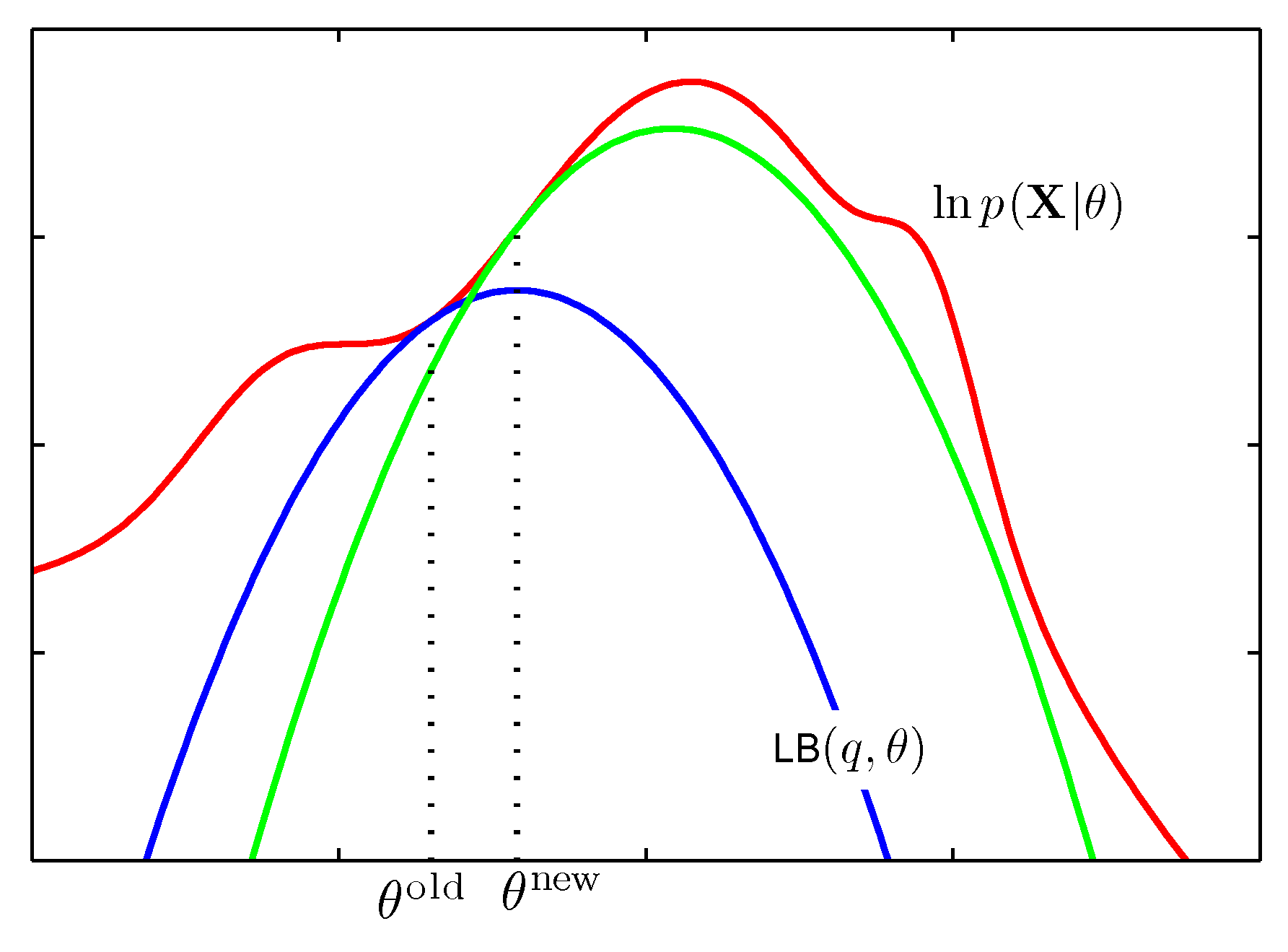
EM Details¶
Maximizing $\mathrm{LB}$ w.r.t. $q$¶
- Note that
and consequenty, maximizing $\mathrm{LB}$ over $q$ leads to minimization of the KL-divergence. Specifically, it follows from Gibbs inequality that $$ q^{(m+1)}(z) := p(z|x,\theta^{(m)}) $$
Maximizing $\mathrm{LB}$ w.r.t. $\theta$¶
- It also follows from (the last line of) the multi-line derivation above that maximizing $\mathrm{LB}$ w.r.t. $\theta$ amounts to maximization of the expected complete-data log-likelihood (where the complete data set is defined as $\{(x_i,z_i)\}_{i=1}^N$). Hence, the EM algorithm comprises iterations of
Hoemwork exercise: EM for GMM Revisited¶
E-step¶
- Write down the GMM generative model
- The complete-data set is $D_c=\{x_1,z_1,x_2,z_2,\ldots,x_n,z_n\}$. Write down the complete-data likelihood $p(D_c|\theta)$
- Write down the complete-data log-likelihood $\log p(D_c|\theta)$
- Write down the expected complete-data log-likelihood $\mathrm{E}_Z\left[ \log p(D_c|\theta) \right]$
M-step¶
Maximize $\mathrm{E}_Z\left[ \log p(D_c|\theta) \right]$ w.r.t. $\theta=\{\pi,\mu,\Sigma\}$
Verify that your solution is the same as the 'intuitive' solution of the previous lesson.
Homework Exercise: EM for Three Coins problem¶
- You have three coins in your pocket. For each coin, outcomes $\in \{\mathrm{H},\mathrm{T}\}$.
Scenario. Toss coin $0$. If Head comes up, toss three times with coin $1$; otherwise, toss three times with coin $2$.
The observed sequences after each toss with coin $0$ were $\langle \mathrm{HHH}\rangle$, $\langle \mathrm{HTH}\rangle$, $\langle \mathrm{HHT}\rangle$, and $\langle\mathrm{HTT}\rangle$
Task. Use EM to estimate most the likely values for $\lambda$, $\rho$ and $\theta$
Report Card on EM¶
- EM is a general procedure for learning in the presence of unobserved variables.
- In a sense, it is a family of algorithms. The update rules you will derive depend on the probability model assumed.
- (Good!) No tuning parameters such a learning rate, unlike gradient descent-type algorithms
- (Bad). EM is an iterative procedure that is very sensitive to initial
conditions! EM converges to a local optimum.
- Start from trash $\rightarrow$ end up with trash. Hence, we need a good and fast initialization procedure (often used: K-Means, see Bishop p.424)
- Also used to train HMMs, etc.
(OPTIONAL SLIDE) The Free-Energy Principle¶
- The negative lower-bound $\mathrm{F}(q,\theta) \triangleq -\mathrm{LB}(q,\theta)$ also appears in various scientific disciplines. In statistical physics and variational calculus, $F$ is known as the free energy functional. Hence, the EM algorithm is a special case of free energy minimization.
- It follows from Eq.1 above that
- The Free-Energy Principle (FEP) is an influential neuroscientific theory that claims that information processing in the brain is also an example of free-energy minimization, see Friston, 2009.
- According to FEP, the brain contains a generative model $p(x,z,a,\theta)$ for its environment. Here, $x$ are the sensory signals (observations); $z$ corresponds to (hidden) environmental causes of the sensorium; $a$ represents our actions (control signals for movement) and $\theta$ describes the fixed 'physical rules' of the world.
(OPTIONAL SLIDE) The Free-Energy Principle, cont'd¶
- Solely through free-energy minimization, the brain infers an approximate posterior $q(z,a,\theta)$, thus inferring our perception, actions, and learning equations.
- Free-energy can be interpreted as (a generalized notion of sum of) prediction errors. Free-energy minimization aims to minimize prediction errors through perception, actions, and learning. (The next picture is from a 2012 tutorial presentation by Karl Friston)

(OPTIONAL SLIDE) The Free-Energy Principle, cont'd¶
- $\Rightarrow$ The brain is "nothing but" an approximate Bayesian agent that tries to build a model for its world. Actions (behavior) are selected to fulfill prior expectations about the world.
- In our BIASlab research team in the Signal Processing Systems group (FLUX floor 7), we work on developing (approximately Bayesian) artificial intelligent agents that learn purposeful behavior through interactions with their environments, inspired by the free-energy principle. Applications include
- robotics
- self-learning of new signal processing algorithms, e.g., for hearing aids
- self-learning how to drive
- Let me know (email bert.de.vries@tue.nl) if you're interested in developing machine learning applications that are directly inspired by how the brain computes. We often have open traineeships or MSc thesis projects available.
open("../../styles/aipstyle.html") do f
display("text/html", read(f, String))
end