%%javascript
IPython.OutputArea.prototype._should_scroll = function(lines) {
return false;}
7 Equilibrium in the Flexprice Model¶
QUESTIONS¶
- In the flexible-price model, what keeps aggregate demand and the level of production equal to potential output?
- In the flexible-price model, what makes the supply of funds—saving—equal to the demand for funds—investment—in financial markets?
- When saving or investment demand changes, what happens n the flexible-price model to the real interest rate, and why?
4.As government policies, the international economic environment, or other features of policy or the economic environment change, what happens in the flexible-price model to^consumption, investment, government, and gross and net export spending?
financial markets: The stock market, the bond market, the short-term borrowing market, plus firms' borrowings from banks.
total saving private saving plus government saving (the government's surplus; government saving is negative when the government runs a deficit) plus foreign saving.
private saving Equal to households' disposable incomes (which include earnings retained by corporations and then reinvested) minus their consumption spending. Household saving includes both saving done directly by households and saving done on their behalf by firms whose stock they own.
government saving: The government's budget surplus. Government saving is negative when the government runs a budget deficit.
foreign saving: The net amount of money that foreigners are committing to buying up property and assets in the home country. Equal to minus net exports.
capital inflow: Net investment by the citizens of one country in another—the "flow" of financial capital from one country to another.
crowding out: Decreases in investment spending caused by a drop in government saving that leads to higher real interest rates.
7.1 Full-Employment Equilibrium¶
Chapter 6 set out the determinants of the components of total spending. But knowing what determines consumption spending C, investment spending I, and net exports NX is not enough for understanding the macroeconomy. The macroeconomy is a system. The determinants of net exports are affected indirectly by the level of investment spending. Investment spending cannot be analyzed without knowing what has happened to consumption spending. But consumption spending depends on income, which in turn depends on the levels of net exports and investment spending.
We need a way of analyzing the macroeconomy as an interdependent system, rather than as a collection of parts we stack next to each other. What are the forces in the economy that make aggregate demand equal output? This question has two answers. One answer is correct when we assume prices, wages, and debts are fully flexible. A second—different—answer is correct when we assume that they are "sticky".
Starting in Chapter 9, we will look at the sticky-price model of the macroeconomy. In this chapter, we assume prices, wages, and debts are fully flexible.
7.1.1 Price Flexibility¶
The key assumption that separates how we analyze equilibrium in this chapter from our analysis that begins in Chapter 9 is the assumption of price flexibility. In this chapter, we assume prices are fully flexible. We must confess: This assumption is not a realistic description of the short run. We use it because assuming prices are flexible is very helpful for analyzing the economy in the long run.
7.1.1.1 If Prices Were Truly Flexible: Some Details¶
What does it mean for prices to be flexible? The authors work in Berkeley, where sometimes it seems every student in a morning class arrives with a paper coffee cup in hand. The lines at one of the most popular cafes, Caffe Strada, typically go out the door just before the 10:00 a.m. classes begin. Everyone in line needs to have their cappuccino, latte, or espresso if they’re going to make it through class. This is especially the case on our foggy, chilly mornings in late spring.
If prices were fully flexible, the price of the coffee drinks would rise between the time the last student got in line and the time she reached the counter. The chill in the air increased demand. The time (morning) increased demand. In a world of fully flexible prices, the price of the product would respond by rising immediately. As you stood there, waiting to reach the counter, you’d see the price of your coffee drink rise. But 45 minutes later, when the sun had burned off the fog so the chill in the air was gone, and when everyone was already in class, the subsequent fall in demand would lead to falling prices. That swing in prices in immediate response to changes in demand would be an example of fully flexible prices. This is, of course, an example on a micro scale. When the same story applies in industry after industry, then you have a macro story.
If prices, wages, and debts were to be fully flexible across the macroeconomy, the amount of output the economy produces Y is always equal to its potential output Y*. So what guarantees that, in a flexible-price economy, this full-employment level of output will also be an equilibrium level of output, where output equals aggregate demand?
It is the real interest rate r that adjusts to ensure full-employment equilibrium in a flexible-price macroeconomy. Now we will see why and how:
7.1.2 The Flow-of-Funds Approach¶
We saw in Chapter 6 that the real interest rate determines investment spending. Also, the real interest rate determines the real exchange rate $ \epsilon $, and this real exchange rate determines net exports. What you will learn in this chapter is that the real interest rate changes and adjusts to make the demand for output equal to the available output—which in this flexible-price economy is potential output Y*. What causes the real interest rate to change and adjust and to rapidly be at the level consistent with full-employment equilibrium? Supply and demand in financial markets cause this as purchasing power—funds—flow into and out of the markets in the economy that finance production and consumption. Thus we call this the flow-of-funds approach to understanding macroeconomic equilibrium in a flexible-price economy.
What is the real interest rate that plays this role? The real interest rate is the price that a lender charges to provide and the price that a borrower pays to acquire financing, which is the social power to control the commitment of resources. Finance flows through the financial markets as savers try to find a productive, profitable, and interest-, dividend-, or capital gains-earning place to put their savings; and as businesses try to find cheap financing for the investment projects they undertake in the hope that they will become profitable.
Why do some people and organizations provide finance—lend money? Because they have no immediate spending use for it, and receiving some interest is better than having it sit under the mattress. Why do businesses borrow money? They borrow money because they hope to make a profit by using the funds they borrow to invest in new plant and equipment in order to expand their operations.
Thus the saving of households and others flows into the financial market, and the borrowing of businesses seeking to finance investment flows out of financial market. The real interest rate is the price charged and received in the financial market. Loanable funds are the commodity that is traded in this market: control over purchasing power today under the condition that such control is only temporary, and that the control over purchasing power will have to be returned—that the loan will have to be paid back.
When the interest rate is at its long-run equilibrium level, the supply of loanable funds equals the demand for loanable funds. The financial market is then in balance.
7.1.2.1 The Paradox of Thrift¶
Chapter 4, recall, presented a truly long-run economic model, a model of economic growth. Remember—or review—that when the saving rate increases in such a long-run model, the capital-output ratio increases to its new steady-state balanced growth-path equilibrium value. More saving thus produces a higher level of productivity and standard of living. But Chapter 4 had no story about how an increase in saving produces a higher capital-labor ratio—it assumed that more savings by individuala automatically translated into higher investment by businesses and a faster-growing capital stock. But there was no clear and explicit mechanism.
There was thus a gap in the argument of Chapter 4. What if there is no mechanism, or if the mechanism fails? What if purchasing power flows into the financial market as households and organizations seek to not consume but save, but the flow of purchasing power out of financial markets is not of equal magnitude? Then savers cannot find enough in the way of investments—stocks, bonds, real estate portfolios, loans—and so they seek to hold some other asset that will allow them to save and thus to carry their purchasing power from the present into the future. What is that other asset? It is cash: money. And so if there is no mechanism—or if the mechanism fails—we then have that excess demand for money that British economist John Stuart Mill put his finger on in 1829 as the cause of a high-unemployment depressed-production "general glut":
Persons... at that particular time... liked better to possess money than any other commodity. Money, consequently, was in request, and all other commodities comparative disrepute... the result is, that all commodities fall in price, or become unsaleable...
If there is no effective mechanism, then increases in desired savings from households and organizations unaccompanied by parallel increases in desired investment spending by businesses can fail to enrich but rather impoverish an economy by causing a depression. John Maynard Keynes (1936) noted in his General Theory of Employment, Interest, and Money that this "paradox of thrift" was of great concern to Thomas Robert Malthus, who argued that the idea that more savings automatically and necessarily generated more investment and greater wealth "of all the opinions advanced by able and ingenious men... appears to me to be the most directly opposed to just theory, and the most uniformly contradicted by experience"; that this paradox most prominently advocated in Bernard de Mandeville's (1721) Fable of the Bees, but can be traced back more than a century earlier to Barthelemy de Laffemas's (1598) Les Trésors et Richesses pour Mettre l'Estat en Splendeur.
Here, however, in the flexprice model of Chapter 7, there is no "paradox of thrift". Here we fill that gap in the Chapter 4 argument. Here there is a mechanism. Chapter 7 provides this answer: the real interest rate is the price that adjusts to ensure that supply and demand are in balance in the flow-of-funds through the fionancial market, and thus that increases in savings lead to more investment. You will learn in this chapter that when saving increases, real interest rates decline, and so investment spending increases. And more investment in plant and equipment produces a larger capital stock, which in the very long run increases the capital-labor ratio, the capital-output ratio, and output per worker.
But this only works when prices, wages, and debts are none of them "sticky".
Note, therefore that there will be a certain tension in this chapter. Prices are flexible; the time scale of the analysis must be long enough for prices to adjust so that there is no excess demand or excess supply in any of the economy’s markets. So this analysis of Chapter 7 applies to changes in the economy only if they take significantly longer than a month or a quarter. On the other hand, we are going to assume that potential output Y* does not change, which means that the analysis of Chapter 7 applies to changes in the economy only if they take significantly less than a decade. The usefulness of the flexible-price model thus tends to get squeezed between the sticky-price fluctuations model covered in later chapters and the long-run growth model covered earlier.
But before we get too far ahead of ourselves, let’s build the model.
7.1.3 RECAP: Full-Employment Equilibrium¶
In a flexible-price economy, real output Y always equals potential output Y*. At equilibrium in output markets, this potential output will equal aggregate demand; this is the flow-of-output approach. We can also look at equilibrium with the flow-of-funds approach; saving equals investment in equilibrium. Changes in the real interest rate will take the economy to equilibrium.
7.2 Two Approaches, One Model¶
<font color="000088>7.2.1 Flow-of-Funds and Flow-of-Output
The goal of this chapter is to show how the real interest rate ensures full-employment equilibrium in an economy with flexible prices. At equilibrium, two statements will be true:
- The supply of funds will equal the demand for funds
- Aggregate demand for output will equal potential output.
The first is a statement about the flow-of-funds into and out of financial markets. The second is a statement about the circular flow of output in the economy, and about "Say's Law"—that there is (in this chapter's flexprice model, at least) no "general glut" of high unemployment and idle productive capacity. In this section, we will show that these two statements—one from the flow-of-funds approach and the other from the circular flow of purchasing power approach—can be mathematically derived from each other.
Why, if the two approaches to this one model are equivalent mathematically, do we bother with two approaches? The answer is worth remembering, because this will not be the last time in your studies of economics that a second, mathematically equivalent, approach is suddenly substituted for an approach you have already figured out. There are times in economics—and this is one of them—when a mathematically equivalent approach has much better and clearer economic intuition than the original approach you already mastered. And the best economics is always the most intuitive story.
We can show that the flow-of-funds approach and the circular flow approach are equivalent ways of modeling the flexible-price economy in two ways. We can show the equivalence with algebra. And we can show the equivalence using the drawing introduced in Chapter 2 of the economy’s circular flow. Let’s start with the circular flow.
7.2.2 Using the Circular Flow Diagram¶
Goods and services—output—are produced in businesses, generating income (the blue flow) for households. Household income includes not just wage and salary income, but interest income, rent income, retained business earnings, and more. Households can do three things with this income (the green flows): consume goods and services that are produced by businesses, pay net taxes to government, or save—household saving—in financial markets. With the net tax revenues, government can buy goods and services from businesses (the pink flow) or accu mulate a surplus (green flow) which it saves in financial markets. Some goods and services are imported from other countries, so not all of the spending for goods and services flows back to domestic businesses; some of it flows to the rest of the world. Imports are at least partially offset by our exports of goods and services to other countries. The difference — imports less exports—represents funds from our economy that accumulate in the rest of the world. This net inflow of financial capital from the rest of the world (red flow) is saved in financial markets.
The financial markets lend the funds saved by households, government, and the rest of the world to businesses, which use the funds to invest in plant and equipment (pink flow). Total saving S is the sum of private saving Sp, government saving Sg, and foreign saving by the rest of the world Sf. So through the financial markets, total saving S equals investment I. This is the flow-of-funds approach to equilibrium.
The sum of consumption spending (pink flow from households), government spending (pink flow from government), investment spending (pink flow from financial markets), less the net imports (red flow to rest of the world) flows into businesses. This is aggregate demand. Businesses produce output in response to this aggregate demand. So through the output markets, aggregate demand equals output. This is the flow-of-output approach to equilibrium. And the output produced by businesses generates income for households. Off we go on another round through the circular flow.
The circular flow diagram is one way to understand that the flow-of-funds and flow-of-output approaches to the macroeconomy are equivalent. We can also demonstrate that equivalence a second way: algebra.
The Circular Flow Diagram: This version of the circular flow is complicated by the addition of the government and financial markets to the diagram. Not all final goods and services are bought by households. Some are bought by the government, which taxes to raise resources to finance itself. Some are bought by businesses seeking to invest, which raise the needed resources by issuing stock, issuing bonds, and borrowing—all of which take place in financial markets. This version is also complicated by its recognizing that there is a world outside, a world that buys the products of domestic businesses and that invests through domestic financial markets.
7.2.3 Using Some Algebra¶
We start from the familiar flow-of-output equilibrium condition, and derive the flow- of-funds equilibrium condition. Begin with the definition of aggregate demand AD:
AD = C + I + G + NX
Under the flow-of-output approach, aggregate demand AD and output Y are equal in macroeconomic equilibrium. When wages and prices are flexible, then output Y equals the economy’s potential productive output Y. So in flow-of-output equilibrium, potential output Y will equal aggregate demand AD. We have
Y* = C + I + G + NX
Now a few steps will take us to the equivalent flow-of-funds equilibrium statement. Subtract consumption C, government purchases G, and net exports NX from both sides in order to move everything except investment spending I to the left-hand side:
Y* - C - G - NX = I
And then a little math trick will give us economically meaningful concepts: Subtract and add net taxes T on the left-hand side by subtracting it from income Y* and adding it to — G. Add some parentheses so we can group terms by economic concepts:
(Y* —T —C) + (T —G) + (-NX) = I
7.2.4 Unpacking the Flow-of-Funds Equation¶
Now let’s step back and look at what this flow-of-funds equation means.
The right-hand side of this equation is simply investment spending I. In the circular flow approach, investment spending is simply spending by firms to build factories and structures and boost their productive capacity. But under the flow-of-funds approach, we think of investment I not as the output that businesses buy, but as the funds that businesses allocate to buying these investment goods. Investment spending I is the flow of funds out of financial markets to businesses, which then use the funds to undertake investment. It is the demand for loanable funds.
The left-hand side of the equation measures the total saving flowing into financial markets from three different groups—private savings via households (which, remember, include not only the workers but also the owners of businesses, and the businesses themselves because they are acting as agents for their owners), the government, and the rest of the world.
The first term:
$ Y^* — T — C $
is equal to private household saving Sp. In this flexible-price model, potential output Y* is equal to real output. Output and household income are always equal. So Y* is just household income. Subtract net taxes T and consumption spending C from household income Y* and what is left? What is left is private saving—the flow of funds from households into financial markets — because saving is the only thing that households do with income, other than pay it to the government as taxes and spend it on consumption goods.
The second term
$ T — G $
is equal to government saving Sg. T is simply the taxes the government collects minus the transfer payments it makes to individuals. G is government purchases. So T — G is the difference between the taxes that the government collects and the transfer payments and purchases the government makes. When T-G is positive, the government is running a budget surplus. The surplus is government saving SG. When T —G is negative, the government is running a deficit (as it is today). Then SG will be less than zero.
The last term—the opposite of net exports, -NX—is foreign saving Sf, saving by foreigners directed into the United States. It is the capital inflow, the net flow of funds that the rest of the world channels into domestic financial markets. Net exports are the difference between the dollars foreigners spend buying our exports and the dollars earned by foreigners selling us imports. If net exports are less than zero—which they typically are for America—foreigners have dollars left over after they buy all our exports they want. These internationally owned dollars flow into financial markets. They aren’t spent buying our exports, and the only other useful thing the rest of the world can do with them is save them. (When net exports are positive, this term has a different interpretation. It is the net amount of domestic saving that is diverted into international financial markets—the amount of saving that does not show up as loanable funds available to finance investment at home, but instead finances investment abroad.)
We have derived the flow-of-funds equilibrium equation. The three left-hand side terms of
$ (Y^*-T-C)+(T- G)+(~NX)=I $
are the three flows of purchasing power into the financial markets: private saving, government saving, and foreign saving. Added together they make up total saving S, which is the supply of loanable funds. The demand for loanable funds is simply investment spending I, the right-hand side of the equation above. So the flow-of-funds equilibrium equation can also be written
$ S^p + S^g + S^f = I $
What we have shown is that the circular-flow equilibrium condition—output equals aggregate demand—is equivalent to the flow-of-funds equilibrium condition—saving equals investment. When one statement is true, the other must also be true. When one is false, the other must also be false. If supply equals demand in the market for loanable funds
$ S^p + S^g + S^f = I $
then aggregate demand in the flexible-price economy is equal to full-employment output. And if output equals aggregate demand in the markets for goods and services, then
$ Y^* = C + I + G + NX $
The Flow of Funds through Financial Markets: Private saving, government saving, and foreign saving flow into financial markets. These funds flow out of financial markets to businesses, which use the funds to finance investment demand—the purchase of new plant and equipment.
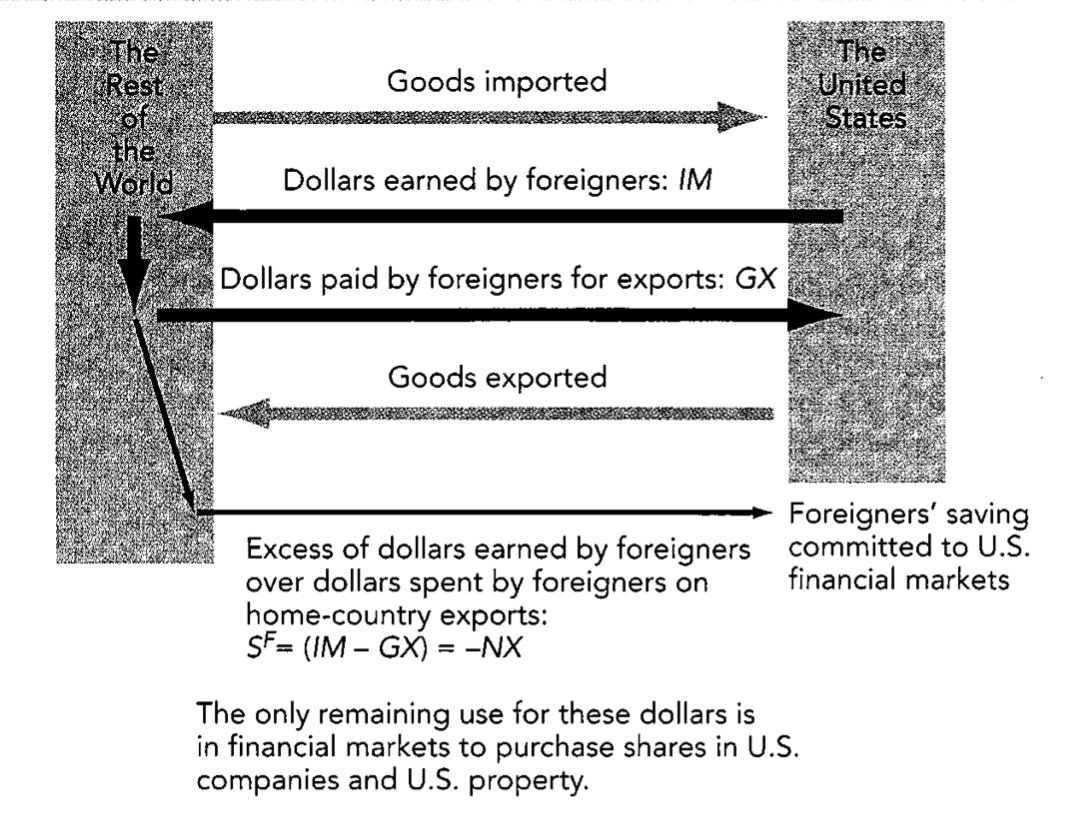
Imports Minus Exports Equals Foreign Saving: Dollars earned by foreigners from selling us imported goods and services return to the United States either as payments for goods and services we export or as foreign sav ing that flows into U.S. financial markets.
7.2.4.1 Financial Transactions And The Flow Of Funds: Some Details¶
The relationship between the funds that flow into and the funds that flow out of financial markets is indirect. When the government runs a surplus, it does not directly lend money to a business that wants to build a new factory. Instead, the government uses the surplus to buy back some of the bonds that it previously issued. The bank that owned those bonds then takes the cash it received from the government and uses it to buy some other financial asset — perhaps bonds issued by a corporation.
Similarly, households or foreigners using financial markets to save rarely buy newly issued corporate bonds. Moreover, they rarely buy shares of stock that are part of an initial public offering. On the rare occasion when they do, they are directly transferring purchasing power to a company undertaking investment. Instead, households and foreigners usually save by purchasing already-existing securities or simply depositing their wealth in a bank.
The relationship between the flows of funds into and out of financial markets is indirect, but it is very real. then the supply and demand in the flow of funds through financial markets balances as well.
7.2.5 RECAP: Two Approaches, One Model¶
We can approach equilibrium in two ways.
One is the circular flow of purchasing power approach: In equilibrium, output equals aggregate demand.
The other is the flow-of-funds approach: In equilibrium, saving equals investment.
We can show that these two approaches are equivalent using the circular flow diagram. We can also show they are equivalent algebraically, by starting with one equilibrium condition, Y = AD, and deriving from it the other, 5 = I.
7.3 The Real Interest Rate Adjusts to Ensure Equilibrium¶
In a flexible-price economy, equilibrium exists when aggregate demand equals potential output. But what economic forces will make aggregate demand equal potential output? The determinants of C, I, G, and NX are things like consumers’ optimism, interest rates, the sensitivity of exports to exchange rates, and so on. These determinants seem to have nothing at all to do with the determinants of Y. It is the form of the production function and the available resources on the sup ply side that determine the level of potential output Y. So what will make the sum of C, I, G, and NX equal potential output?
The answer is: The real interest rate r plays the key role. If government policy, the international economic environment, or domestic conditions change, then the real interest rate changes in response. In turn, the change in the real interest rate causes changes in investment spending, the exchange rate, and net exports. The real interest rate will continue to change until the economy is again at equilibrium. It is these changes in the real interest rate that ensure that in the long run a flexible- price macroeconomy reaches and stays at equilibrium where aggregate demand equals potential output.
But how could a disequilibrium between aggregate demand and output lead to a change in the real interest rate? Here is where the flow-of-funds approach comes in. Equilibrium with aggregate demand equal to potential output is equivalent to equilibrium with the supply of funds—saving—equal to the demand for funds—investment. When aggregate demand is less than potential output, saving is greater than investment. And when aggregate demand is greater than potential output, investment is greater than saving.
When the supply of funds—saving—is greater than the demand for funds—investment—what will happen? The price of loanable funds—the real interest rate r—will fall. Some financial institutions—banks, mutual funds, venture capitalists, insurance companies, whatever—will find purchasing power piling up as more money flows into their accounts than they can find good projects to commit to. They will try to underbid their competitors. How do they underbid? They underbid by saying that they will accept a lower interest rate than the current real interest rate.
As the real interest rate falls, two things happen. The number and value of investment projects that are profitable rise. Investment spending rises, closing the gap between saving and investment (and, not coincidentally, closing the gap between aggregate demand and potential output). And net exports rise, decreasing foreign saving and further closing the gap between saving and investment (and, again not coincidentally, further closing the gap between aggregate demand and potential output). The process will stop when the interest rate has fallen just enough to make the flow of saving into the financial markets equal to investment. So that’s the big bottom line: The real interest rate ensures equilibrium in the flexible-price model because both investment and saving respond to changes in the real interest rate.
<font color="000088"7.3.1 Graphing the Saving-Investment Relationship
We can depict these relationships graphically. Investment spending is the demand for loanable funds. As the real interest rate r falls, investment spending I rises.
Total saving is the supply of loanable funds. It has three components: private saving Sp, government saving Sg (which is usually negative), and foreign saving S<supf.
Let’s start with foreign saving. As the real interest rate r falls, foreign saving falls. The intuition is a bit roundabout. As the real domestic interest rate falls, the nominal and real exchange rates rise. When the real exchange rate s rises, gross exports GX rise. When gross exports rise, net exports NX rise, which is the same thing as saying net imports (—NX) fall. When net imports fall, net foreign inflow of financial capital falls. And net foreign inflow of financial capital is just a long phrase for foreign saving. It is important to remember that foreign saving can be either negative or positive. When a country runs a trade surplus, foreign saving is negative. When it runs a trade deficit, as the United States has been doing for many years, foreign saving is positive. To remind ourselves that foreign saving can be negative or positive, we draw the foreign saving curve crossing the vertical axis.
The Demand for Loanable Funds: The demand for loanable funds is investment de mand. When the real interest rate falls, the number and value of prof itable investment projects rise, increasing businesses' demand for loanable funds to finance investment.
Foreign Saving: The Supply of Loanable Funds from Foreigners: The supply of loanable funds from foreigners is foreign saving. When the domestic real interest rate falls, foreigners will move some funds out of dollar- denominated assets and into assets denominated in other currencies, decreasing foreign saving as nominal and real exchange rates rise.
Private and Government Supply of Loanable Funds: Private saving Sp does not change when the real interest rate r changes. The distance from the vertical axis to the household saving line measures the amount of funds that flow into financial markets from households. If households dissave, so that SH is negative, the household saving line is to the left of zero. Government saving Sg also does not change when the real interest rate r changes. The distance from the vertical axis to the government saving line would measure the amount of funds that flow from financial markets to the government. If the government runs a deficit, so that SGis negative, the government saving line is to the left of zero.
Total Saving: The Supply of Loanable Funds: Total saving is the sum of foreign, household, and government saving. Total saving increases as the real interest rate rises because of the relationship between the real interest rate and foreign saving.
Private saving is another component of total saving. It is what’s left over after net taxes T and consumption C have been subtracted from household income. Consumption spending depends on income, as do net taxes. But as we noted in Appendix 6a, real interest rates do not affect consumption. And because we are assuming that household income is always equal to potential output Y*, which depends on the supplies of inputs and the production function, then income is not dependent on the real interest rate. And since neither the tax rate nor income depends on the real interest rate, net taxes don’t change when the real interest rate changes. So private saving Sp does not change when the real interest rate changes. We show the relationship between household saving and the real interest rate as a vertical line.
Government saving Sg is the final component of total saving. But its value also does not depend on the value of the real interest rate. So here again, we would show the relationship between government saving and the real interest rate as a vertical line. If government saving was negative—if the government was running a deficit—then the government saving line would be to the left of zero.
Total saving is the sum of foreign, household, and government saving. Graphically, we take the foreign saving line, shift it over by the amount of household saving, and shift it over again—or in the case of a government budget deficit shift it back—by the amount of government saving. This gives us the relationship between total saving S and the real interest rate
We now have the two sides of the loanable funds market. The demand for loanable funds is investment spending. The supply of loanable funds is total saving. Bring them together to see the market for loanable funds. When total saving S equals investment demand I, the market for loanable funds is in equilibrium.
7.3.2 The Adjustment to Flow-of-Funds Equilibrium¶
Suppose that the real interest rate is initially greater than the equilibrium real interest rate. Saving will exceed investment by the amount labeled “excess saving.” Some lenders will offer to accept a lower inter est rate. As interest rates fall, investment spending will increase, moving along the investment demand curve. And as interest rates fall, foreign saving will fall, moving along the total saving curve. The macroeconomy will move to the equilibrium interest rate, where saving equals investment. And, as we showed above, when saving equals investment, aggregate demand equals potential output. When prices are fully flexible, the real interest rate adjusts to ensure full employment.
Equilibrium in the Flow of Loanable Funds: The market for loanable funds is in equilibrium when the supply of loanable funds—total saving S—equals the demand for loanable funds—investment demand.
Excess Saving in the Market for Loanable Funds
7.3.3 RECAP: The Real Interest Rate Adjusts to Ensure Equilibrium¶
In the flexible-price model, the real interest rate is the price that equilibrates the market for loadable funds—the place where saving flows into and investment financing flows out of financial markets. What happens if the flow of funds does not balance—if at the current real interest rate, the flow of saving into the financial markets exceeds the demand by corporations and others for purchasing power to finance investment? Then the price of loans—the real interest rate—will fall, until the supply of funds—saving—equals the deriiand for funds—investinent. Conversely, if investment demand exceeds saving, the real interest rate will rise. When the real interest rate is at its equilibrium value, saving equals investment: S = I. Moreover, aggregate demand equals full-employment real GDP: AD = Y*.
7.4 Using the Model: What Makes the Real Interest Rate Change?¶
We can use this graphical way of looking at the flow of funds to figure out what happens to the equilibrium real interest rate when there is some change in the eco nomic environment or in economic policy. Some changes make either the saving or the investment curve shift. Other changes also affect the slope of the saving or investment curve. When one or both of the curves shift or change slope, there will be a new equilibrium real interest rate.
Let’s take a look:
<font color="000088>7.4.1 The Effect of a Change in Saving
Total saving S is the sum of private, government, and foreign saving. So a decrease in any of those components of 5 will decrease total saving. It could be a decrease in household saving, decreasing Sp. It could be an increase in government spending, which decreases government saving Sg. It could be a decrease in our imports, which decreases foreign saving Sf. Any of these changes would be shown by a shift to the left of the total saving S curve.
As an example, let’s suppose the economy is in equilibrium when policy makers decide to increase annual government purchases by the amount $ {\Delta}G $. More government purchases mean less government saving. Less government saving means that the supply of saving in the loanable funds market is shifted to the left: At each possible interest rate, total saving flowing into the loanable funds market is decreased.
At the original real interest rate, investment demand will now exceed total saving. This shortfall in saving will cause the real interest rate r to rise; some borrowers bid up interest rates in an attempt to obtain funding for their investment projects. But the rising interest rate squeezes other borrowers out of the market; the total quantity of funds demanded for investment falls, moving us up and to the left along the inves ment demand curve. The rising domestic real interest rate also lowers the real exchange rate s and increases foreign saving flowing into domestic financial markets, moving us along the second total saving curve. The real interest rate will rise until saving again equals investment. In the end, the flow-of-funds market settles down to equilibrium at a new, higher equilibrium interest rate r with a new, lower level of investment.
When the supply of loanable funds S decreases, the real interest rate r rises, investment spending falls, and (not surprisingly) the amount of saving falls. But notice what has happened: The final change in investment and saving, shown along the horizontal axis, is smaller than the change in saving that threw the flow-of-funds markets out of equilibrium. How could that be? The final change in saving is smaller than the initial change in saving because foreign saving rose when the real interest rate rose. But this rise in foreign saving is relatively small so, overall, saving still falls.
A Decrease in Saving Increases the Real Interest Rate: When government purchases rise or taxes are cut, government saving is lowered. The drop in total saving leads to higher real interest rates, increased financing of investment by foreigners, and a fall in investment spending by businesses. Economists worry about the long-run effects of rising govern ment deficits because of their effect on capital accumulation.
A drop in household saving Sp would be analyzed the same way, as would a drop in foreign saving SF that occurred at every interest rate. In both of these cases, the total saving curve shifts to the left, raising the real interest rate, increasing foreign saving slightly to offset part but not all of the initial drop in saving, and decreasing investment demand.
A tax cut has a slightly different effect. It is very like the effect of a government purchases increase. But because a tax cut increases disposable income and the mar ginal propensity to consume is less than 1, there is one difference. The difference is that a portion of the addition to household income from the tax cut shows up as household saving. So the initial shift to the left of the total saving curve is smaller than the drop in government saving by the amount of this change in house hold saving. Otherwise the effects are very similar: Like a government purchases increase, a tax cut leads to an increase in the interest rate, a rise in foreign saving, and a fall in investment spending.
Why do economists make such a big deal out of a decrease in government saving—whether it’s due to a decrease in taxes or an increase in government purchases? Because as Figure 7.10 illustrates, in the long run, a decrease in gov ernment saving—an increase in the budget deficit—makes interest rates rise, which reduces investment spending. And remember one of the lessons of the standard of living. In the long run, increases in government borrowing “crowd out"—reduce-—investment spending, which, all else equal, slows the country’s rate of economic growth while the economy adjusts to a lower balanced-growth path.
7.4.2 The Effect of a Change in Investment Demand¶
We can also use the flow-of-funds graph to see the effect of an increase in investment I. Suppose that businesses suddenly become more optimistic about the future and increase the amount they wish to spend on new plant and equipment (as they did in the late 1990s). What would be the effect of such a domestic investment boom?
Investment—the demand-for-loanable-funds curve—shifts to the right. At the initial interest rate, investment demand now exceeds saving. Firms that wish to increase their investment spending will bid up interest rates as they compete for scarce loans.
As interest rates rise, two things simultaneously happen:
One, other firms will decrease their investment spending because their planned investment projects are no longer profitable at these now-higher interest rates—a movement along the new investment demand curve.
Two, the higher real interest rate leads to a fall in the real exchange rate, to a fall in net exports, and thus to an increase in foreign saving flowing into domestic financial markets—a movement along the saving curve. In the end, the loanable funds market settles at a higher interest rate with an increased level of saving and investment.
Notice what happened: The higher interest rates due to the first shift in investment led to a subsequent decrease in investment that partly—but not entirely—offset the initial shift. So investment did increase. What made the increase in investment possible? The increase in foreign saving. If saving had not increased in reaction to the higher interest rates, investment could not increase.
Without an increase in saving, the shift in investment demand would make interest rates rise so much that investment spending would fall right back to its initial position. Instead, when foreign saving increases with real interest rates, both saving and investment increase in response to increased business optimism.
An Increase in Investment Also Increases the Real Interest Rate: Increased investment demand leads to higher real interest rates, which dampen business enthusiasm for new investment projects while increasing financing of investment by foreigners.
7.4.3 RECAP: Using the Model: What Makes the Real Interest Rate Change?¶
We can use the graphical approach to flow-of-funds equilibrium to see that an increase in saving or a decrease in investment—shifts to the right in the sav ing curve or to the left in the investment demand curve—would lead to a fall in the real interest rate. And a decrease in saving or an increase in investment would make the real interest rate rise. When the supply of saving shifts, the ultimate change in saving will be smaller than the initial change in saving. When investment demand shifts, the ultimate change in investment will be smaller than the initial change in investment. In both cases, this is due to changes in the real interest rate which induce movements along the saving and investment curves that partly offset the initial shifts.
7.5 Calculating the Equilibrium Real Interest Rate: Algebra¶
The flow-of-funds graphs let us figure out whether interest rates rise or fall in reaction to a change in policy or economic environment that affects investment demand or total saving. But what if we are policy makers who want to know the precise value of the real interest rate at equilibrium, and by how much the interest rate will change if we implement some policy? To figure out the value of the interest rate and how much it changes in reaction to a change in policy or economic envi ronment, we need to do some algebra.
What we need are the equations for total saving S and for investment demand I. Equilibrium occurs when saving S equals investment I, so we will just set the equa tions equal to each other. Then we solve for the real interest rate.
This sounds straightforward—and it is. But the equations can get quite messy. Don’t get discouraged. If the notation and the algebra get to be a bit much, remem ber that all we’re doing is setting saving equal to investment and solving for r.
7.5.1 The Formula for the Equilibrium Real Interest Rate¶
Start with total saving S, which is the sum of private saving Sp, government saving Sg, and foreign saving Sf:
$ S = S^p + S^g + S^f $
Private saving is equal to total income Y minus net taxes T minus consumption spending C. But since we are in a world of flexible prices (that’s our assumption in this chapter, remember), total income Y is always equal to potential output Y. Consumption spending depends on baseline consumption c0, the marginal propensity to consume cy, the tax rate t, and potential income Y. Remember, net taxes are a constant proportion of income: T = tY. Thus:
$ S^p = Y^* - T - C = Y^* - tY^* - \left(c_0 + c_y(1-t)Y^*\right) $
Government saving is equal to net taxes T minus government purchases G.
$ S^g = T - G = tY^* - G $
Note that neither private saving nor government saving depends on the real interest rate. That is why we graph private saving Sp and government saving Sg as vertical lines on every graph with the interest rate r on the vertical axis.
On the other side of the flow-of-funds equilibrium equation, demand for funds is simply investment spending, which depends on animal spirits $ I_0 $, the sensitivity of investment spending to the real interest rate $ I_r $, and the level of the real interest rate r. When the real interest rate r rises, investment spending I falls:
$ I = I_0 - \left(I_r\right)r $
7.5.1.1 If Trade Were Balanced¶
Suppose trade were balanced. Then foreign savings Sf would be zero. And our flow-of-funds equilibrium equation would become:
$ S^p + S^g + 0 = Y^* - tY^* - \left(c_0 + c_y(1-t)Y^*\right) + tY^* - G = I $
Which simplifies to:
$ Y^* - c_0 - c_y(1-t)Y^* - G = I_0 - \left(I_r\right)r $
And solving for r:
$ r^* = \frac{I_0 + c_0 + \left[(1-t)c_y - 1\right]Y^*}{I_r} $
At this value of $ r^* $, domestic aggregate demand is equal to Y*—enough to carry employment to full employment and production to potential output.
7.5.1.2 But Trade Is Not Balanced¶
However, trade is not balanced. So what about foreign saving Sf?
Foreign saving is imports minus exports. The determinants of foreign saving are three parameters—the propensity to import imy, foreigners’ propensity to buy exports xf, and the sensitivity of exports to the exchange rate $ x_{\epsilon} $—and three variables: foreign incomes Yf, domestic total income Y*, and the exchange rate $ \epsilon $:
$ S^f = -NX = {im_y}Y^* - {x_f}Y^f - x_{\epsilon}\epsilon $
And it is the exchange rate that changes when the real interest rate r changes:
$ \epsilon = {\epsilon}_0 - {{\epsilon}_r}(r- r^f) $
where the real exchange rate $ \epsilon $ depends on the baseline value of the real exchange rate, the sensitivity of the real exchange rate to changes in interest rates, the domestic real interest rate r, and the foreign real interest rate $ r^f $.
Thus, because foreign saving depends on the exchange rate, and because the exchange rate depends on the interest rate, foreign saving Sf depends on the real interest rate r. When the real interest rate rises, the total saving flow increases. Why? Because an increase in the real interest rate attracts foreign capital into domestic financial markets and increases foreign saving:
$ S^f = -NX = {im_y}Y^* - {x_f}Y^f - x_{\epsilon}\left({\epsilon}_0 - {{\epsilon}_r}(r- r^f)\right) $
The flow-of-funds equilibrium is where supply and demand balance: where total saving is equal to investment spending. So now we solve this equation for r*, the equilibrium real interest rate, which will equal:
$ r^* = \frac{I_0 + G + c_0 - \left[1 - (1-t)c_y + im_y\right]Y^* + {x_f}Y^f + x_{\epsilon}\left({\epsilon}_0 + {{\epsilon}_r}r^f\right)}
{I_r + x_{\epsilon}{\epsilon}_r} $
This equation is a little unappetizing: you cannot be expected to remember it.
It is, however, worthwhile because you can refer to it. And referring to it will allow you to analyze what pretty much any sudden shock will do or what pretty much any counterfactual scenario will mean for a flexprice economy.
7.5.1.3 Deriving the Equilibrium Interest Rate Equation¶
Unless you are fascinated, feel welcome to skip this subsection. It is important to get the intuition: the interest rate shifts up or down to keep the flow-of-funds through financial markets in supply-and-demand balance, and that rapidly drives the flexprice economy to its full-employment production-equal-to-potential equilibrium. But the details are to be referred to when needed, not memorized: there are better things to keep in your brain in these days of high information technology.
To derive the equation for the equilibrium real interest rate, we start from either the flow-of-output or the flow-of-funds equilibrium statement:
$ Y = C + l + G + NX $ or $ S^p + S^g + S^f = I $
They are eqiuivalent. Many students like to start from $ Y=C+f+G+ NX $ simply because it is more familiar. If you do, you will have to plug-and-chug in a slightly different way, for here we begin with the flow-of-funds equilibrium equation:
$ S^p + S^g + S^f = I $
Recall that private saving, taxes, and consumption spending are:
$ S^p = Y - T - C $
$ T = tY $
$ C = c_0 + c_y(1-t)Y $
Substituting gives us:
$ S^p = Y - tY - c_0- c_y(1 - t)Y $
Recall that government saving is:
$ S^g = T - G = tY - G $
And recall that foreign saving is:
$ S^f = IM - GX = - NX = (im_y)Y - (x_fY^f + x_{\epsilon}{\epsilon}) $
Plugging in for the components of the savings flow-of-funds into financial markets gives us:
$ (Y - tY - c_0 - c_y(1 - t)Y) + (tY - G) + ((im_y)Y - (x_fY^f + x_{\epsilon}{\epsilon})) = I $
We can simplify this a little:
$ (1-im_y - c_y(1-t))Y - c_0 - G - x_fY^f - x_{\epsilon}{\epsilon} = I $
Investment spending is:
$ I = I_0 - I_rr $
Plugging in:
$ (1-im_y - c_y(1-t))Y - c_0 - G - x_fY^f - x_{\epsilon}{\epsilon} = I_0 - I_rr $
Recall the exchange rate:
$ \epsilon = {\epsilon}_0 + {\epsilon}_r(r^f - r) $
Plug it in:
$ (1-im_y - c_y(1-t))Y - c_0 - G - x_fY^f - x_{\epsilon}({\epsilon}_0 + {\epsilon}_r(r^f - r)) = I_0 - I_rr $
Separating out the terms with r in them:
$ I_rr + x_{\epsilon}{\epsilon}_rr = c_0 + I_0 + G + x_fY^f + x_{\epsilon}{\epsilon}_0 + x_{\epsilon}{\epsilon}_rr^f - (1-im_y - c_y(1-t))Y $
and dividing through:
$ r^* = \frac{I_0 + G + c_0 - \left[1 - (1-t)c_y + im_y\right]Y^* + {x_f}Y^f + x_{\epsilon}\left({\epsilon}_0 + {{\epsilon}_r}r^f\right)}
{I_r + x_{\epsilon}{\epsilon}_r} $
And so we are done.
Once agai: It is important to get the intuition: the interest rate shifts up or down to keep the flow-of-funds through financial markets in supply-and-demand balance, and that rapidly drives the flexprice economy to its full-employment production-equal-to-potential equilibrium. But the details are to be referred to when needed, not memorized: there are better things to keep in your brain in these days of high information technology.
7.5.2 Interpreting the Equilibrium Real Interest Rate Equation¶
What does this equation:
$ r^* = \frac{I_0 + G + c_0 - \left[1 - (1-t)c_y + im_y\right]Y^* + {x_f}Y^f + x_{\epsilon}\left({\epsilon}_0 + {{\epsilon}_r}r^f\right)}
{I_r + x_{\epsilon}{\epsilon}_r} $
say?
First look at the numerator. When $ I_0 $ increases—when business "animal spirits" rise as those sitting on businesses' investment approval committees get more optimistic and excited—the real interest rate r will increase. A rise in $ I_0 $ is an increase in the demand for financing in the loanable funds market—and when demand goes up, the price, which is the real interest rate $ r $, tends to rise.
When $ G $ increases—when the government spends more and borrows more in order to finance its spending, thus decreasing public saving—the real interest rate $ r $ will rise. When $ c_0 $ gets larger—when consumers get more confident and are more eager to spend on consumption goods, thus reducing private saving—the real interest rate $ r $ will rise. And when incomes abroad $ Y^f $ rise, thus boosting demand for our exports and redirecting dollars earned from our imports away from invsetment in America, thus reducing foreign saving, the real interest rate $ r $ will rise. All three of these are reductions in saving: in government saving, private saving, and foreign saving, respectively. And when the supply of savings flowing into the loanable funds market declines, the price, which is the real interest rate $ r $, tends to rise.
Were $ Y $ to increase—it usually does not rise in calculations involving the flexprice model, as supply-and-demand balance in the labor market enforces $ Y = Y^* $, output equal to potential—the price in the flow-of-funds through the financial market, the real interest rate $ r $, would decline. Other things being equal, a richer country would save more, by an amount equal to a fraction $ (1-im_y - c_y(1-t)) $ times the increase in national income, and such an increase in savings supply would lower the price that is the real interest rate $ r $.
By how much does the real interest rate rise in respone to such changes in economic policy and in the economic environment? We get the answer to this question by looking at the denominator: $ I_r + x_{\epsilon}{\epsilon}_r $. The larger the denominator, the smaller the incressse in the real interest rate $ r $ when business animal spirits or any other factor tending to raise it rises. Why? The first term $ I_r $ captures the change in investment due to a change in the real interest rate. The larger the sensitivity of investment to interest rates $ I_r $, the flatter the investment demand curve; the more quickly and farther investment spending will fall in response to a rise in interest rates as the economy moves along a flatter investment demand-for-financing curve. Thus the smaller will be the rise in interest rates needed to restore equilibrium in the flow-of-funds through the financial market.
The second term $ x_{\epsilon}{\epsilon}_r $ tells us how much foreigners' desired investments in America change in response to a change in the real interest rate $ r $. With a higher real interest rate foreign savings invested in America are more profitable, hence foreigners want to undertake more of them. The larger is the product $ x_{\epsilon}{\epsilon}_r $, the flatter is the total saving curve on a graph with total savings $ S^p + S^g + S^f $ on the horizontal and the real interest rate $ r $ on the vertical axis; the larger is the change in foreign saving when the real interest rate rises as the economy moves along a flatter savings supply-of-finance curve. And the larger the relative change in foreign saving, the less the real interest rate $ r $ will be pulled up.
The Slope of the Investment Curve Affects the Size of Changes in the Real Interest Rate
With the algebraic equations, we can calculate the equilibrium value of the real interest rate. To do so requires the value of all of those constants in the equilibrium equation above. Often, however, the information is given to us not as a list of values of parameters such as the marginal propensity to consume $ c_y $ and so on, but as equations for the four components of aggregate demand. Here again, we can calculate the equilibrium value of the real interest rate. We just remember that equilibrium occurs when saving S equals investment I, which is the same thing as aggregate demand AD equals output Y.
7.5.2.1 Calculating The Equilibrium Real Interest Rate from Parameter Values: An Example¶
Assume the parameters of the model are:
- $ I_0 = 3650 $ baseline "animal spirits" for business investment spending
- $ Y^* = 20000 $ potential output is 20,000 billion dollars a year
- $ c_0 = 750 $ baseline "consumer confidence" for household consumption spending
- $ c_y = 0.75 $ marginal propensity to consume
- $ t = 0.15 $ tax rate
- $ G = 3750 $ government purchases
- $ im_y = 0.15 $ propensity to purchase imports
- $ x_f = 0.10 $ foreigners' propensity to purchase exports with rising income
- $ Y^f = 25000 $ foreigners' relevant income
- $ x_{\epsilon} = 500 $ foreigners' propensity to purchase exports with a rising value of foreign currency
- $ {\epsilon}_r = 10 $ foreign exchange speculators' tolerance for risk in an attempt to capture higher interest rates
- $ {\epsilon}_0 = 0 $ foreign exchange speculators' view of the long-run likely value of the exchange rate
- $ r^f = 0.02 $ foreign real interest rate
- $ I_r = 20000 $ responsiveness of investment spending to the interest rate
- $ \epsilon = 0 $ exchange rate, as deviation from baseline
- $ {\epsilon}_0 = 0 $ foreign exchange speculators' views of exchange rate fundamentals, as deviation from baseline
To find the equilibrium real interest rate, we substitute these values into the equation for the real interest rate:
$ r^* = \frac{I_0 + G + c_0 - \left[1 - (1-t)c_y + im_y\right]Y^* + {x_f}Y^f + x_{\epsilon}\left({\epsilon}_0 + {{\epsilon}_r}r^f\right)}
{I_r + x_{\epsilon}{\epsilon}_r} $
$ r = \frac{3650 + 750 + 3750 + (0.10)(25000) - (1-0.15 - (0.75)(1-0.15))Y + (500)(10)(0) + (500)(10)(0.02)}{20000 + (500)(10)} $
and then simplify.
$ r = 0.02
7.5.2.2 Calculating the Equilibrium Real Interest Rate from Aggregate Demand Equations: An Example¶
Suppose that we had the same economy that was described in Box 7.4, but instead of being given the values of the parameters, we were given the aggregate demand equations themselves:
- $ Y = Y^* = 20000 $
- $ C = 750 + 0.75(1 - 0.15)Y $
- $ I = 3650 - 20000r $
- $ G = 3750 $
- $ GX = (0.1)(25000) + (500)(10)(0) + (500)(10)(0.02 - r) $
- $ IM = (0.15)Y
- $ NX = GX - IM $
First, combine the expressions for gross exports and imports to get:
$ NX = -(0.15)Y - (500)(10)r $
Now how do we find the equilibrium real interest rate? In the flexprice model's equilibrium, output Y is equal to potential output Y* which equals aggregate demand AD, which is the sum of consumption C, investment I, government G, and net exports NX. Thus:
$ Y^* = Y = C + I + G + NX $
- $ Y = Y^* = 20000 $
- $ C = 750 + 0.75(1 - 0.15)Y = 13500 $
- $ I = 3650 - 20000r $
- $ G = 3750 $
- $ GX = (0.1)(25000) + (500)(10)(0) + (500)(10)(0.02 - r) = 2600 - 5000r $
- $ IM = (0.15)Y = 3000
- $ NX = - 5000r - 400 $
$ 20000 = 13500 + 3750 + 3650 - 20000r - 400 - 5000r $
$ 20000 = 20500 - 25000r $
$ r = 0.02 $
When the economy is in equilibrium, the real interest rate will be 0.02, or 2 percent per year.
7.5.3 Determining the Effect of a Change in Fiscal Policy on Aggregate Demand¶
7.5.3.1 Baseline and Alternative Scenarios, and $ \Delta $ Differences¶
With the graphs of saving and investment, we were able to figure out whether the interest rate would increase or decrease. Now we can figure out the effect of a change in policy on the real interest rate and on the values of consumption, investment, government purchases, and net exports. Let’s use a familiar example: an increase in government purchases G.
The equilibrium real interest rate is:
$ r^* = \frac{I_0 + G + c_0 - \left[1 - (1-t)c_y + im_y\right]Y^* + {x_f}Y^f + x_{\epsilon}\left({\epsilon}_0 + {{\epsilon}_r}r^f\right)}
{I_r + x_{\epsilon}{\epsilon}_r} $
Now let us suppose that the economy's baseline is some equilibrium in which this equation is satisfied, that we want to consider an alernative in which we have perturbed some element of the economic environment or economic policy, and then calculate:
$ {\Delta}r^* = r_{alt} - r_{base} $
and similarly use " $ \Delta $ " to denote the difference between alternative-scenario and baseline-scenario values of all relevant variables and parameters. In this " $ \Delta $ " notation, our equation for the equilibrium real interest rate becomes:
$ {\Delta}r^* = \frac{{\Delta}I_0 + {\Delta}G + {\Delta}c_0 - \left[1 - (1-t)c_y + im_y\right]{\Delta}Y^* + {x_f}{\Delta}Y^f + x_{\epsilon}\left({\Delta}{\epsilon}_0 + {{\epsilon}_r}{\Delta}r^f\right)}{I_r + x_{\epsilon}{\epsilon}_r} $
We can immediately simplify this because we are considering only a change in government purchases $ G $. There is no change to consumer confidence, to business animal spirits, to the level of potential output, to relevant foreign output, to interest rates abroad, or to foreign exchange speculators' views of the fundamental value of the exchange rate. All of these that do not change between the baseline and the alternative scenarios become zeros. With so many zeros, there is very little left of the equation above:
$ {\Delta}r^* = \frac{{\Delta}G}{I_r + x_{\epsilon}{\epsilon}_r} $
The size of the change in the equilibrium real interest rate comparing the baseline to the alternative scenario depends on the sensitivity of investment to changes in the real interest rate, the sensitivity of exports to a change in the real exchange rate, the sensitivity of the real exchange rate to a change in domestic real interest rates—which multiplied togethert are the sensitivity of foreign savings to changes in the domestic real interest rate—and the difference in governmetn purchases. That is all.
7.5.3.2 Other Components of Aggregate Demand¶
With government purchases rising, what happens to the other components of aggregate demand? The change in government purchases has no effect on consumption. Because potential output does not change, national income does not change. National income, baseline consumption, the tax rate, and the marginal propensity to consume do not shift, so there is no effect on the consumption function. Thus the change in consumption spending is zero:
$ {\Delta}C = 0 $
The shift in government purchases has an indirect effect on investment. Investment depends on the interest rate, and the interest rate will change as a result of the change in government purchases. So we see that investment spending will change by:
$ {\Delta}I = -I_r{\Delta}r = \frac{I_r{\Delta}G}{I_r + x_{\epsilon}{\epsilon}_r} $
Investment spending thus falls when government spending rises. This is what we call "crowding out": The rise in government purchases increases real interest rates, which “crowds out” private investment spending.
Nothing in the international economic environment—our propensity to import, foreigners’ propensity to buy our exports, foreign exchange speculators' optimism or pessimism, or foreign interest rates—changes when domestic fiscal policy changes. Nor does the level of potential output change. But look back at our exchange rate equation:
$ \epsilon = {\epsilon}_0 + {\epsilon}_r(r^f - r)
Thus a change $ {\Delta}r $ in the domestic real interest rate will change the exchange rate, the value of foreign currency, by an amount
$ {\Delta}\epsilon = - {\epsilon}_r{\Delta}r $
This will in turn change exports by an amount:
$ {\Delta}NX = {\Delta}GX = - x_{\epsilon}{\epsilon}_r{\Delta}r $
Last, real GDP does not change because potential output does not change, and this is a long-run full-employment model, with real GDP always equal to potential output:
$ {\Delta}Y = {\Delta}Y^* = 0 $
The change in aggregate demand is the sum of the changes in consumption, investment, government purchases, and net exports:
$ {\Delta}AD = {\Delta}C + {\Delta}I + {\Delta}G + {\Delta}NX $
$ {\Delta}AD = 0 -I_r{\Delta}r + {\Delta}G - x_{\epsilon}{\epsilon}_r{\Delta}r $
And substituting in $ {\Delta}r^* $:
$ {\Delta}AD = 0 - \frac{I_r{\Delta}G}{I_r + x_{\epsilon}{\epsilon}_r} + {\Delta}G - \frac{x_{\epsilon}{\epsilon}_r{\Delta}G}{I_r + x_{\epsilon}{\epsilon}_r} $
$ {\Delta}AD = {\Delta}G - \frac{I_r{\Delta}G}{I_r + x_{\epsilon}{\epsilon}_r} - \frac{x_{\epsilon}{\epsilon}_r{\Delta}G}{I_r + x_{\epsilon}{\epsilon}_r} $
$ {\Delta}AD = {\Delta}G - {\Delta}G $
$ {\Delta}AD = 0 $
The change in aggregate demand is 0! The increase in government spending AG is just offset by the decreases in investment spending and net exports. Aggregate demand does not change when government spending changes because this is a long-run model in which we have assumed that real GDP is always equal to its potential value $ Y^* $. In this flexprice business-cycle long-run model, a change in the economic environment or economic policy that shifts one of the components of aggregate demand leads to a reallocation of aggregate demand but doesn’t change the overall value of aggregate demand.
7.5.3.3 The Effect on Saving¶
What effect does an increase in government purchases have on total saving S? Since neither household income nor consumption changes, private household saving does not change:
$ {\Delta}S^p = 0 $
Government purchases, however, do change. Since government saving is taxes minus government purchases, and since government purchases have gone up, the change in government saving is
$ {\Delta}S^g = - {\Delta}G $
Foreign saving is the opposite of net exports, so foreign saving changes by:
$ {\Delta}S^f = - {\Delta}NX = x_{\epsilon}{\epsilon}_r{\Delta}r = \frac{x_{\epsilon}{\epsilon}_r{\Delta}G}{I_r + x_{\epsilon}{\epsilon}_r} $
Put all these pieces together and we get
$ {\Delta}S = {\Delta}S^p + {\Delta}S^g + {\Delta}S^f = -{\Delta}G + \frac{x_{\epsilon}{\epsilon}_r{\Delta}G}{I_r + x_{\epsilon}{\epsilon}_r} = \frac{I_r{\Delta}G}{I_r + x_{\epsilon}{\epsilon}_r} $
The change in total saving just equals the change in investment. This is precisely what we ought to have expected. The increase in government purchases reduces the flow of saving into financial markets. The interest rate rises. The higher interest rate reduces businesses’ plans for investment spending but also calls forth additional saving from foreigners. And so the higher interest rate has returned the flow-of-funds through finacial markets to supply-and-demand balance.
Note that the falls in investment and in total saving are not as large as the rise in government purchases. This is also what we snojl have expected. The increase in government purchases reduced the flow of domestic saving into financial markets, but the increased flow of foreign-owned capital into the market partially offset this reduction. The extra foreign saving kept the decline in invest ment from being as large as the rise in government purchases.
What is the point of the march through the algebra? It allows us to calculate not just qualititative but quantitative effects: to know not just that the interest rate will go up, but by how much the interest rate will go up, and what its effects will be on different pieces of the economy.
7.5.3.4 Trumponomics: Increased Government Purchases: An Example¶
Consider the economy with its parameters as they were in section 7.5.2 above. Suppose that we have an increase in annual government purchases $ {\Delta}G $ of 200 billion. For those parameter values, the algebraic effects of an increase in government purchases on the economy become arithmetically:
$ {\Delta}r^* = \frac{{\Delta}G}{20000 + (500)(10)} = \frac{{\Delta}G}{25000} = \frac{200}{25000} = 0.008 $
$ {\Delta}C = 0 $
$ {\Delta}I = -\frac{20000{\Delta}G}{20000 + (500(10)} = 0.8{\Delta}G = -160 $
$ {\Delta}\epsilon = - 10{\Delta}r = - 0.08 $
$ {\Delta}NX = {\Delta}GX = - (500)(10){\Delta}r = -40 $
$ {\Delta}Y = {\Delta}Y^* = 0 $
$ {\Delta}AD = {\Delta}C + {\Delta}I + {\Delta}G + {\Delta}NX = 0 - 160 + 200 - 40 = 0 $
A 200 billion increase in government purchases, a 160 billion decrease in investment spending, a 40 billion reduction in gross and net exports, no change in aggregate demand, an 0.8 percentage-point increase in the real interest rate, and an 8 percent increase in the value of the exchange rate, in the value of foreign currency, are what the flexprice model with these parameter values predicts.
This is of interest because an increase in government purchases of about 200 billion dollars at an annual rate is one of President Donald Trump's two successful initiatives in economic policy in the first two years of his presidency.
The Shift in U.S. Fiscal Policy from the Election of Donald Trump
Back in 2015-2016 it appeared as though the United States was on a trajectory to attain a federal deficit path in which the federal government budget deficit was about 3.0 percent of GDP—about the average over 1968-2017. Such a deficit was perfectly sustainable, given a nominal GDP growth rate of 5.0 percent per year, at a stable debt-to-annual-GDP ratio of 60 percent. Such a deficit was a big change from the Clinton years, when we were actually running surpluses—a circumstance I played a small part in creating, and of which I am very proud. But such a deficit had become normal. Ronald Reagan broke the mold. After Reagan, politicians no longer seriously sought to get the budget to balance—except for Bill Clinton and his Democatic congressional majorities of 1993-94. This is one reason I do have considerable affection for Bill Clinton, in spite of his problems with his zipper, his love for "welfare reform", and assorted other things.
The 3 percent of GDP deficit was also a big change from the Great Recession years of 2009, 2010 and 2011, when the government was stepping up and spending a lot more than it was taking in taxes both to boost employment—because there was a lot of unemployment then—and because tax revenues are depressed when employment and production are depressed.
But with the coming of Donald Trump to the presidency, things shifted. The U.S. is now on a trajectory to a deficit of 5 percent of GDP. This does not appear unsustainable: At least, investors are very willing to hold us government bonds even though we have this substantial deficit. But it is a sizeable change.
Roughly half of this increase is a consequences of the late-2017 Republican corporate tax cut. Roughly half of this increase is a consequences of the early-2018 breaking of the institutional and procedural barriers that had put downward pressure on spending. These two were the two initiatives in economic policy that the Trump administration succeeded in implementing.
Here we are just examining the second—the roughly 200 billion permanent increase in annual spending. Supposing that the Federal Reserve manages to use the tools at its disposal to keep the economy near full employment, it is entirely appropriate to use the flexprice model to analyze its effects. And we have just done so:
- real interest rate $ r $ increases: up 0.008 (by 0.8 percentage points, measured as an annual rate).
- government purchases $ G $ increase: up by 200 billion at an annual rate.
- investment spending $ I $ declines: down by 160 billion at an annual rate.
- gross exports $ GX $ and net exports $ NX $ decline: down by 40 billion at an annual rate.
- the exchange rate, the value of foreign currency $ \epsilon $ rises in value: up by 0.08 (by 8 percent, as the value of the dollar declines and the dollar depreciates).
Reduced annual investment spending of 160 billion means that the United States is investing 500 dollars per person fewer each year building up its capital stock. That is large enough, perhaps, to take one-tenth a percent per year off the economic growth rate of the country as a whole. Unless you think that the United States is investing too much—that we are building too many houses and installing too many machines in factories—that should be somewhat worrisome. And the fall in exports means that the U.S. trade deficit is now higher by 40 billion a year.
These effects of Donald Trump's policies are not what he ordered. He came into office wanting, above all, to eliminate the trade deficit. He came into office wanting, second of all, to boost American economic growth. Yet those are not what this policy is tending to do. And this is one of two signature accomplishments.
7.5.3.5 Trumponomics: Increased "Animal Spirits" and Investment¶
President Trump's second signature accomplishment—and the other 200 billion of the increase in the annual federal budget deficit—was the late-2017 corporate tax cut. Normally a tax cut would shift the economy toward increasing consumption spending. But this was not a normal tax cut. Its benefits were concentrated very high up in the wealth ladder—it is those with the tens of millions of dollars of wealth, and more, who received extra money. The marginal propensity to consume $ c_y $ for this group is very close to zero. Thus the first effect was to diminish government $ S^g $ by about 200 billion at an annual rate, and boost private saving $ S^p $ by about 200 billion at an annual rate, leaving investment spending and interest rates unchanged.
The other point of the tax cut besides the wealth transfer was to induce more investment in America by making corporate investments more profitable: lower corporate tax rates leave higher corporate after-tax profits. The administration claimed that these added incentives would rapidly boost investment in America, adding about 800 billion to annual investment. That would have been a large increase in $ {\Delta|I} $ indeed. What effect would it have had on the economy?
Looking at the "changes" differentials between the baseline no-tax cut and the alternative tax-cut scenario, the important pieces of the flexprice model are:
$ {\Delta}I = {\Delta}I_o - I_r{\Delta}r $
$ {\Delta}{\epsilon} = -{\epsilon}_r{\Delta}r $
$ {\Delta}GX = x_{\epsilon}{\Delta}{\epsilon} $
$ {\Delta}S^f = - {\Delta}GX $
$ {\Delta}I = {\Delta}S^f $
And the effect on the equilibrium real interest rate, with our parameter values, is:
$ {\Delta}r* = \frac{{\Delta}I_o}{I_r + x_{\epsilon}{\epsilon}_r} $
$ = \frac{800}{20000 + (500)(10)} = + 0.032 $
The real interest rate goes up by another 3.2 percentage points. And:
$ {\Delta}I = {\Delta}I_o - I_r{\Delta}r = 800 - (20000)(.032) = +160 $
$ {\Delta}{\epsilon} = -{\epsilon}_r{\Delta}r = -(10)(0.032) = -0.32 $
$ {\Delta}GX = x_{\epsilon}{\Delta}{\epsilon} = (500)(-0.32) = -160 $
Investment spending would have gone up by 160 billion at an annual rate—cancelling the drag on investment placed by the government purchases increase.
The exchange rate—the value of foreign currency—would have fallen by 32 percent, as the dollar underwent an enormous boom.
And the annual trade balance would have worsened by an additional 160 billion dollars.
Needless to say, that is not what happened in reaction to the late-2017 tax cut. There was no surge in the dollar.
What went wrong? Well, the Trump administration—ably assisted by tame economists in universities and think-tanks—vastly overstated how powerful the corporate tax cut was going to be as an incentive to boost investment.
# calibrating the flexprice model to the U.S. economy today
# consensus parameter values...
Y = 20000
C = 13500
I = 3250
G = 3750
GX = 2500
IM = 3000
NX = GX-IM
I_0 = 3650
I_r = 20000
e_r = 10
x_e = 500
t = 0.15
c_0 = 750
c_y = 0.75
im_y = 0.15
x_f = 0.10
Y_f = 25000
e = 0
r = 0.02
C_calc = c_0 + c_y*(1-t)*Y
I_calc = I_0 - I_r*r
GX_calc = x_f*Y_f + x_e*e_r*e
GX_calc
0.0
7.5.4 RECAP: Calculating the Equilibrium Real Interest Rate
We can use the flexible-price model to calculate the equilibrium real interest rate. With equations for the components of aggregate demand and the value of potential output, we can use the flow-of-funds equilibrium condition—set total saving equal to investment—and solve for equilibrium real interest rate r. Or we can use the flow-of-output equilibrium condition-set aggregate demand equal to output—and solve for equilibrium r. Either approach gives the same result.
We can then use the equilibrium real interest rate and our knowledge of the economic environment to calculate the equilibrium values of the components of aggregate demand and total saving. And we can then use that model solution as a springboard to calculate how the economy’s equilibrium will change in response to changes in the environment or in policy.
Conclusion¶
This chapter has analyzed a flexible-price macroeconomy in the short run—a time span in which neither labor nor capital stocks have an opportunity to change enough to materially affect the level of potential output. It has taken a snapshot of the economy in equilibrium at a point in time. Note that this equilibrium is not the balanced growth-path equilibrium of the Solow Growth Model: it is a different equilibrium concept. This equilibrium is one in which there are no pressures for any of the components of aggregate demand, C, I, G, GX, or NX, to change; and no pressures for either the real interest rate r or the real exchange rate $ \epsilon $ to change immediately.
This chapter has asked how the equilibrium would be different if the economic environment or economic policy were different. It has at times implicitly talked about the dynamic evo lution of the economy in the short run by describing the economy as shifting from one equilibrium to another in response to a change in policy or in the environment.
Remember that there is a tension: Prices are flexible enough and the time span is long enough for the real wage to adjust to keep output equal to potential, for the price level to adjust to keep aggregate demand equal to output, and for the real interest rate and the real exchange rate to adjust so that the components of aggregate demand sum up to its total. Yet the time span is short enough that potential output does not materially change via investment, labor-force growth, and growth in the efficiency-of-labor. We are thus caught between the long-run model of Chapters 4 and 5 and the upcoming sticky-price properly short-run model of Chapters 9 to 12.
Nevertheless, the flexible-price model presented here can be powerful. It allows us to say a great deal about the way various kinds of shocks will affect the economy and the composition of total spending and output—as long as full employment is maintained. But note that full employment does not have to be maintained by the adjustment of flexible prices. It can also be maintained by clever and appropriate policy. And as long as the central bank and the fiscal authorities are successful at maintaining full employment, the flexprice model is a useful and appropriqte tool.
Moreoever, we have been able to resolve the big mystery of Chapter 4: How we can be certain that a change in desired savings translates into increased investment and thus a higher capital stock.
In the flexible-price model, the interest rate plays the key role in keeping the economy in balance: keeping aggregate demand equal to potential output and the economy at full employment. Changes in economic policy and the economic environment induce changes in the mix of spending. They shift the proportions of aggregate demand between consumption, investment, government purchases, and net exports. But they do not affect the level of aggregate demand. Things that reduce saving—whether they reduce household saving, government saving, or the capital inflow—raise interest rates and reduce investment. Changes in economic policy and in the economic environment that increase saving lower interest rates and increase investment.
Think back to Chapters 4 and 5, where long-run growth depended on the economy’s saving-investment rate. Here we have seen how a great many changes in economic policy and in the economic environment affect saving and investment. There are powerful links in the long run between shifts that change equilibrium interest rates and the economy’s long-run growth path. Drawing those links explicitly would be too hard and too complicated. Nevertheless, when doing analyses using this chapter’s flexible-price model remember that this chapter’s assumption that the level of potential output is not changed by different levels of investment spending is just a “snapshot” simplifying assumption. In the long run of Chapters 4 and 5, changes in investment have powerful effects on production and prosperity.
We have covered a lot of ground in this chapter. However, it is worth emphasizing what this chapter has not done:
As the paragraphs above stressed, this chapter has not dealt with the impact of changes in policy and the economic environment on economic growth, which was done in Chapters 4 and 5. Refer to those chapters to analyze how changes in saving and investment ultimately affect productivity and material standards of living in the long run.
It has ignored the nominal financial side of the economy—money, prices, and inflation—completely.
It has maintained the full-employment assumption—that notion will be relaxed in the chapters starting with Chapter 9.
Catch Our Breath¶
- Ask me two questions…
- Make two comments…
- Further reading…
Lecture Support: http://nbviewer.jupyter.org/github/braddelong/LSF18E101B/blob/master/Equilibrium_in_the_Flexprice_Model.ipynb
Equilibrium in the Flexprice Model: https://www.icloud.com/keynote/0eT-yTiDbnFJG75PcmVtFrsRg
Equilibrium in the Flexprice Model: PRESENTATION SLIDES¶
We have just stormed through chapter 6—the building blocks of the business cycle model chapter:
- Read appendix 6a on how consumption is differently affected by permanent and transitory shifts in Y
Now we will move on to chapter 7: Equilibrium in the flexprice business cycle model
- We will take a little peak inside the national income identity
- C + I + G + NX = AD: that’s aggregate demand—spending
- How do we know that is equal to Y—useful output produced, and sold?
- We understand that K, E, L, and labor market equilibrium pushes w/p to a level at which firms want to employ everyone.
- But then what determines where it all goes?
Well, What If Not? What If Aggregate Demand AD > Y Production?¶
- Businesses have inventories…
- They run those inventories down…
- They react by raising prices…
- Unless something else happens to increase dollar spending, rising prices mean that the same spending flow of nominal dollars is a lower real aggregate demand for goods and services…
- And so we have inflation—a general rise in the price level—and real aggregate demand falls to match Y = Y☆ as the same spending flow buys fewer goods…
- This chain of logic won’t work when we get to sticky prices…
Well, What If Not? What If Aggregate Demand AD > Y Production?¶
- Businesses have inventories…
- They will find those inventories building up…
- They will cut prices…
- Unless something else happens to decrease dollar spending, falling prices mean that the same spending flow of nominal dollars is a higher real aggregate demand for goods and services…
- And so we have deflation—a general rise in the price level—and real aggregate demand rises to match Y = Y☆ as the same spending flow buys more goods…
- This chain of logic won’t work when we get to sticky prices…
Pause to Note: This AD = Y = Y* Is Not a Terribly Good Assumption¶
- It is not even a terribly good assumption if one qualifies it by “after five years”
- Asymmetry in changes
- Falls below, not fluctuations around
- But we use it as a benchmark
- And it can apply to the real world:
- After 10 years, with no big shocks
- After 3 years, if somebody is making Y = Y☆ by successful demand management policy
Calculating Flexprice Equilibrium¶
Three prices: W/P, P, r
- W/P to set $ Y = Y^*$: the "labor market"
- P we will get to in chapter 8—the "money market"
- r: the flow-of-funds through financial markets
Move to a different form of the national income identity
$ Y = C + I + G + NX $
$ Y - C - T - NX = I + (G-T) $
$ (Y - C - T) - NX + (T-G) = I $
$ S_p + S_f + S_g = I $
Now We Have Something We Can Work with!¶
We have not just an equation: we have a process
$ S_p(Y, t) + S_f(\epsilon, ...) + S_g = I(r) $
- If $ S_p + S_f + S_g > I $...
- People will be scrambling to buy the bonds and stocks issued by companies to finance their investment spending...
- The prices of bonds and stocks will go up...
- Which is the same thing as the interest rate r falling...
- As r falls, I increases: it is more profitable to build building and install machines...
- As r falls, ε—the exchange rate, the value of foreign goods/currency—rises...
- As domestic goods appear cheaper, foreigners spend more of their dollars buying domestic exports...
- And spend fewer adding to the savings pool...
- Thus $ S_f $ goes down and $ I $ goes up...
- Until r has fallen enough and ε has adjusted enough to bring $ S = I $ into balance...
- And those movements in r and ε drive changes in exports and investment spending...
Now We Have Something We Can Work with!¶
- If $ S_p + S_f + S_g < I $, then...
- Companies will be scrambling to sell the bonds and stocks they issued to finance their investment spending...
- The prices of bonds and stocks will go down...
- Which is the same thing as the interest rate r going up...
- As r rises, I falls: it is no longer as profitable to build building and install machines...
- As r rises, ε—the exchange rate, the value of foreign goods/currency—falls...
- As domestic goods appear more expensive, foreigners spend less of their dollars buying domestic exports...
- And spend more adding to the savings pool...
- Thus $ S_f $ goes up and $ I $ goes down...
- Until r has fallen enough and ε has adjusted enough to bring $ S = I $ into balance...
- And those movements in r and ε drive changes in exports and investment spending...
Catch Our Breath¶
- Ask me two questions…
- Make two comments…
- Further reading…
Lecture Support: http://nbviewer.jupyter.org/github/braddelong/LSF18E101B/blob/master/Equilibrium_in_the_Flexprice_Model.ipynb
Keynote File: https://www.icloud.com/keynote/0eT-yTiDbnFJG75PcmVtFrsRg
Solving the Flexprice Model¶
Savings and Investment Functions¶
The private savings function
$ Y - C - T = S_p $
$ Y - (c_o + c_y(1-t)Y) - T = S_p $
$ Y - (c_o + c_y(1-t)Y) - tY = S_p $
$ (1 - c_y - t + c_{y}t)Y - c_o = S_p $
Government savings
$ S_g = T - G = tY - G $
Foreign Savings
$ S_f = - NX = IM - GX $
$ S_f = im_{y}Y - x_fY^f - {x_{\epsilon}}{\epsilon} $
$ S_f = im_{y}Y - x_fY^f -$
$ {x_{\epsilon}}\left({\epsilon}_o + {\epsilon}_r\left(r^f - r\right)\right) $
Investment
$ I = I_o - {I_r}r $
Solving using $\Delta$s¶
- Start at full employment
- $ \Delta $: deviations from full-employment
- Hence:
$ {\Delta}Y = 0 $
$ {\Delta}C = {\Delta}c_o + {c_y}(1-t){\Delta}Y $ :: consumption
$ {\Delta}I = {\Delta}I_o - {I_r}{\Delta}r $ :: investment
$ {\Delta}G $ :: government
$ {\Delta}NX = x_f{\Delta}Y^f + {x_{\epsilon}}{\Delta}{\epsilon} - im_y{\Delta}Y $ :: international
$ {\Delta}\epsilon = {\Delta}{\epsilon}_o + {\epsilon}_r\left({\Delta}r^f - {\Delta}r\right) $ :: exchange rate
- Then trace changes through...
An Increase in Government Purchases of ΔG...¶
- Start at full employment
- $ \Delta $: deviations from full-employment
- Hence:
$ {\Delta}G = {\Delta}G $
$ {\Delta}Y = 0 $
$ {\Delta}S_p + {\Delta}S_f + {\Delta}S_g = {\Delta}I $
$ {\Delta}S_p + {\Delta}S_f - {\Delta}G = {\Delta}I $
$ {\Delta}S_p = (1 - c_y - t + c_{y}t){\Delta}Y - {\Delta}c_o = 0 $
$ 0 + {\Delta}S_f - {\Delta}G = {\Delta}I $
$ {\Delta}S_f = im_{y}{\Delta}Y - x_f{\Delta}Y^f - {x_{\epsilon}}\left({\Delta}{\epsilon}_o + {\epsilon}_r\left({\Delta}r^f - {\Delta}r\right)\right) $
$ {\Delta}S_f = x_{\epsilon}{\epsilon}_r{\Delta}r $
$ {\Delta}I = {\Delta}I_o - {I_r}{\Delta}r $
$ 0 + x_{\epsilon}{\epsilon}_r{\Delta}r - {\Delta}G = -{I_r}{\Delta}r $
$ -{\Delta}G = -\left({I_r} + x_{\epsilon}{\epsilon}_r\right){\Delta}r $
$ {\Delta}r = \frac{{\Delta}G}{{I_r} + x_{\epsilon}{\epsilon}_r} $
$ {\Delta}I = -I_{r}{\Delta}r = \frac{-I_{r}{\Delta}G}{{I_r} + x_{\epsilon}{\epsilon}_r} $
$ {\Delta}GX = {\Delta}NX = -{x_{\epsilon}}{\epsilon}_r{\Delta}r = \frac{-{x_{\epsilon}}{\epsilon}_{r}{\Delta}G}{{I_r} + x_{\epsilon}{\epsilon}_r} $
$ {\Delta}I + {\Delta}GX = -{\Delta}G $
A Decrease in Animal Spirits ${\Delta}I_o $... ¶
- Start at full employment
- $ \Delta $: deviations from full-employment
- Hence:
$ {\Delta}I = {\Delta}I_o - I_r{\Delta}r $ :: investment
$ {\Delta}Y = 0 $ :: full employment is maintained
$ {\Delta}S_p + {\Delta}S_f + {\Delta}S_g = {\Delta}I $ :: flow-of-funds
$ {\Delta}S_g = t{\Delta}Y - {\Delta}G = 0 $ :: government savings
$ {\Delta}S_p + {\Delta}S_f + 0 = {\Delta}I_o - I_r{\Delta}r $ :: it's a zero...
$ {\Delta}S_p = (1 - c_y - t + c_{y}t){\Delta}Y - {\Delta}c_o = 0 $ :: pvt dom svgs
$ 0 + {\Delta}S_f + 0 = {\Delta}I_o - I_r{\Delta}r $ :: it's a zero
$ {\Delta}S_f = im_{y}{\Delta}Y - x_f{\Delta}Y^f - x_{\epsilon}{\Delta}{\epsilon}_o - {x_{\epsilon}}{\epsilon}_r\left({\Delta}r^f - {\Delta}r\right) $ :: foreigners
$ {\Delta}S_f = 0 - 0 - 0 - x_{\epsilon}{\epsilon}_r\left(0 - {\Delta}r\right) $ :: one term nonzero
$ x_{\epsilon}{\epsilon}_r{\Delta}r = {\Delta}I_o - I_r{\Delta}r $ :: flow-of-funds
$ \left(I_r + x_{\epsilon}{\epsilon}_r\right){\Delta}r = {\Delta}I_o $
$ {\Delta}r = \frac{{\Delta}I_o}{I_r + x_{\epsilon}{\epsilon}_r} $ :: Change in r
$ {\Delta}I = {\Delta}I_o - I_r{\Delta}r = {\Delta}I_o - \frac{I_r{\Delta}I_o}{I_r + x_{\epsilon}{\epsilon}_r} = \frac{x_{\epsilon}{\epsilon}_r{\Delta}I_o}{I_r + x_{\epsilon}{\epsilon}_r} $ :: Change in I
$ {\Delta}GX = - {\Delta}S_f - x_{\epsilon}{\epsilon}_r{\Delta}r = -\frac{x_{\epsilon}{\epsilon}_r{\Delta}I_o}{I_r + x_{\epsilon}{\epsilon}_r} $ :: Change in GX
$ {\Delta}S_p + {\Delta}S_f - {\Delta}G = {\Delta}I $
$ {\Delta}S_p = (1 - c_y - t + c_{y}t){\Delta}Y - {\Delta}c_o = 0 $
$ 0 + {\Delta}S_f - {\Delta}G = {\Delta}I $
$ {\Delta}S_f = im_{y}{\Delta}Y - x_f{\Delta}Y^f - {x_{\epsilon}}\left({\Delta}{\epsilon}_o + {\epsilon}_r\left({\Delta}r^f - {\Delta}r\right)\right) $
$ {\Delta}S_f = x_{\epsilon}{\epsilon}_r{\Delta}r $
$ {\Delta}I = {\Delta}I_o - {I_r}{\Delta}r $
$ 0 + x_{\epsilon}{\epsilon}_r{\Delta}r - {\Delta}G = -{I_r}{\Delta}r $
$ -{\Delta}G = -\left({I_r} + x_{\epsilon}{\epsilon}_r\right){\Delta}r $
$ {\Delta}r = \frac{{\Delta}G}{{I_r} + x_{\epsilon}{\epsilon}_r} $
$ {\Delta}I = -I_{r}{\Delta}r = \frac{-I_{r}{\Delta}G}{{I_r} + x_{\epsilon}{\epsilon}_r} $
$ {\Delta}GX = {\Delta}NX = -{x_{\epsilon}}{\epsilon}_r{\Delta}r = \frac{-{x_{\epsilon}}{\epsilon}_{r}{\Delta}G}{{I_r} + x_{\epsilon}{\epsilon}_r} $
$ {\Delta}I + {\Delta}GX = -{\Delta}G $
Implications¶
- ΔIo is negative here…
- So the interest rate r falls…
- So investment spending I falls—but not by as much as the fall in ΔIo here…
- Consumption C, government spending G, and national income Y are unaffected…
- Imports IM are unaffected…
- So something must go up when I goes down? What is that something?
- GX:
- A lower interest rate produced by less optimism about their investments by businesses here at home discourages the inflow of foreign saving…
- And raises the value of foreign currency—the exchange rate…
- Hence U.S. exports look more tempting to foreigners…
Catch Our Breath¶
- Ask me two questions…
- Make two comments…
- Further reading…
Lecture Support: http://nbviewer.jupyter.org/github/braddelong/LSF18E101B/blob/master/Equilibrium_in_the_Flexprice_Model.ipynb
Keynote File: https://www.icloud.com/keynote/0eT-yTiDbnFJG75PcmVtFrsRg