Econ 135 Scratch¶
Economics 135:¶
History of Economic Growth¶
Brad DeLong¶
Department of Economics and Blum Center, U.C. Berkeley; and WCEG; last revised: 2020-01-12
Original course by Melissa Dell (Harvard Econ 1342 https://canvas.harvard.edu/courses/8254/assignments/syllabus), revised by Brad DeLong, research assistance by Anish Biligiri
https://bcourses.berkeley.edu/courses/1487685
To Your Clickers…¶
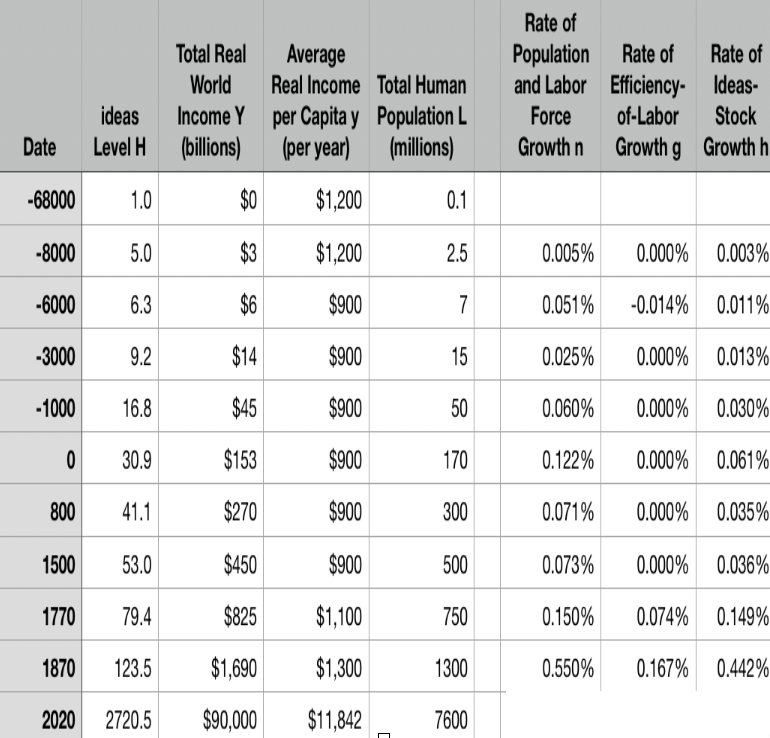
Approximately what was the growth rate of the human useful-ideas stock between the year 0 and 1500?
- About 0.036%/year
- About 3.6%/year
- About 2.06%/year
- About 0.206%/year
- None of the above are close
How Should You Have Calculated the Answer?¶
What should you have had in the front of your minds? What in the back of your minds? What chain of reasoning should you have used?
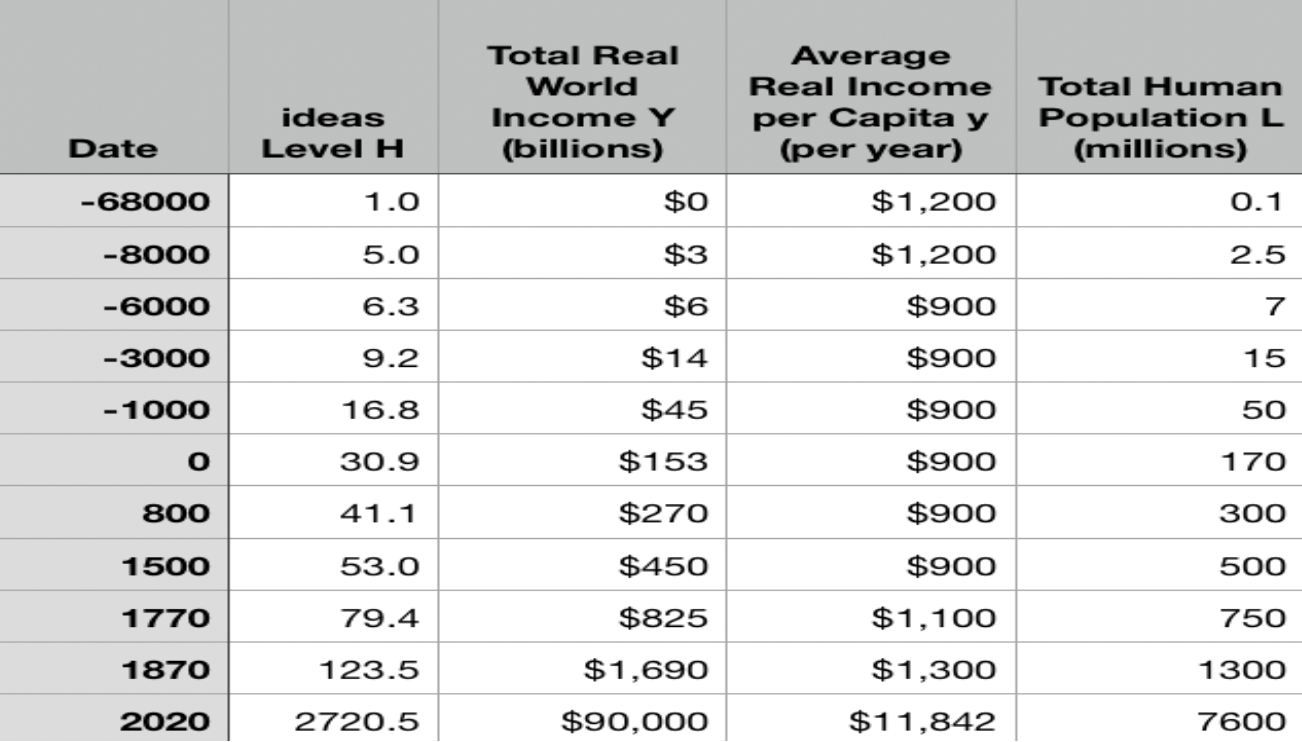
One Table: Average Global Numbers¶
- About 0.036%/year
- About 3.6%/year
- About 2.06%/year
- About 0.206%/year
- None of the above are close
Why Is This Interesting?
2.06/.0036 is about 60, no?
- What else do you find interesting about this table to the left?
Pre-Class Reading: Aristotle¶

Gustave Dore: Dante and Virgil meet the past’s great thinkers in Hell’s Limbo
Dante Alighieri (1320): Inferno:
Poi ch'innalzai un poco più le ciglia,
vidi il maestro di color che sanno
seder tra filosofica famiglia...
(When I had lifted up my brows a little,
The Master I beheld of those who know,
Sit with his philosophic family.
All gaze upon him, and all do him honour.
There I beheld both Socrates and Plato,
Who nearer him before the others stand…)
- Partha Dasgupta (2007): Economics: A Very Short Introduction, selections https://delong.typepad.com/files/dasgupta-economics.pdf
- Aristotle: Politics, Book I https://delong.typepad.com/files/aristotle-politics-book-i.pdf
Dasgupta is for section.
Let’s look at Aristoteles son of Nikomachus of Stagira…
- -384 Stagira to -322 Euboea
- Lyceum, Peripatetic
- THE Philosopher: “the Master… of those who know”
- 1650 years after his death, Aristotle’s is the most powerful intellectual name that Dante can conjure with
- Deepest thinker, trying hard to get it right, most respected intellectual landmark for millennia
- But you are going to hit Aristotle and think: “this is weird”—and a lot of it is weird, and even repugnant
Nevertheless, We Read Aristotle…¶

Raphael: The School of Athens: Plato and Aristotle in Conversation
A mighty, flawed thinker we can learn from:
His thought is mighty
Many have taken his thought—even where it is flawed—to be mighty
We have a lot to learn from him—even if often what we have to learn is not what he sets out to teach…
Note his (implicit and explicit) starting points…
Critically evaluate his arguments: where do we get off and where can we rejoin his cable-car?
Aristotle: Politics¶

Aristotle: Roman marble copy of a Greek bronze by Lysippos (-330)
- For a Greek man to have a functional household, and for Greek men to have a functional city-state, they need resources
- Politics Book I is what Aristotle believes people thinking about politics need to know about acquiring, maintaining, and managing resources
- It is what Aristotle has to say about what we would call the economy
- And we are interested in what Aristotle’s writings here tell us about economic growth
- About what Aristotle’s thoughts are about economic growth
- About the broader intellectual currents in which Aristotle was then swimming
- About the economy in which he was embedded, and about its process of growth—or of not-growth
Questions¶

Classical Athenian 4-drachma silver coin: The “owl”, with the head of the goddess Athene on the front and her familiar bird of wisdom on the back, of the type that Aristotle (or his slaves) would have carried on their person. Weighs 3/5 of an ounce. The Athenian navy paid its oarsmen one drachma a day.
- What assumption that Aristotle made—perhaps (probably?) without thinking about it, because it seemed most obvious to him—struck you as the most wrong or repugnant or weird?
- What does Aristotle say are the four tasks of the Greek man in managing his household? Why these four?
- What role do the “statues of Daedalus, [and] the tripods [robotic catering vessels] of Hephaestus” play in Aristotle’s argument about how the economy of his age is, must be, and should be structured?
- What role does Aristotle’s claim that “Of the art of acquisition [ktêtike] then there is one kind which by nature is a part of the management of a household…. There is another… commonly and rightly called an art of wealth-getting [chrêmatistikê]… [with] the notion that riches and property have no limit…” play in his argument?
- At the end of the first long paragraph of I.11, Aristotle writes: “Of the several divisions of wealth-getting I now speak generally; a minute consideration of them might be useful in practice, but it would be tiresome to dwell upon them at greater length now…” An alternative translation would say “detailed and exact discussion would be useful for the practical workings but to spend too much time on such things is crude…” (see Josiah Ober (2019): Agamemnon’s Cluelessness https://delong.typepad.com/files/ober-agamemnon-1.pdf). Aristotle considers knowledge of the art of wealth-getting “not unworthy of philosophy”, but spending your time practicing this art “illiberal an irksome”; philosophers should know how Thales of Miletos got rich by cornering the olive-press market on the island of Lesbos, but for Aristotle, his students, or his readers to dwell upon these matters at greater length would be “tiresome” or “crude”. What do you think is going on in Aristotle’s mind here?
- Did you find any advice—even indirect and oblique advice—from Aristotle in this passage about what the economic policy of a city-state should be? If so, what was it? If not, why do you think he fails to offer advice here (he offers lots of advice as to the organization and policies of city-states later on in the book)?
- Near the start of Book I Aristotle divided household management into four branches: (1) master-slave, (2) gender roles, (3) human reproduction, and acquiring material resources. he then skipped over (2) and (3) to talk about (1) and (4). Near the very end of the Book I, in I.12, he returns to (2) and (3). He says that “A husband and father, we saw, rules over wife and children, both free, but the rule differs, the rule over his children being a royal, over his wife a constitutional rule”. What is the distinction that you think Aristotle is drawing here? How important is it? (And do note that Aristoteles is here having an argument with Sokrates and Platon, who believed in gender equity: that the souls and thus “the courage and justice of a man and of a woman, are…the same…”
- What does Aristotle conclude, at the end of the book, is the proper way to rank in importance the different branches of the art of household management?
Memo: Guesses at the Population of Athens (and Piraeus)¶
-1000: 4000
-750: 10000
-550: 30000
-450: 75000
-350: 60000
-250: 40000
-150: 30000
-50: 15000
Further Reading¶
- Dante Alighieri (1320): Inferno http://www.gutenberg.org/files/41537/41537-h/41537-h.htm
- Aristoteles of Stagira (-340): Nikomakhean Ethics, V Justice https://delong.typepad.com/files/aristotle-nicomachean-5.pdf
- Gustave Dore (1861): Illustrations for Dante’s “Divine Comedy” https://www.google.com/books/edition/The_Doré_Illustrations_for_Dante_s_Divi/R2TkMiHSOjUC
- Andy Matuschak (2019): Why Books Don’t Work https://andymatuschak.org/books/
- Ian Morris (2005): The Growth of Greek Cities in the First Millennium BC https://www.princeton.edu/~pswpc/pdfs/morris/120509.pdf
- Josiah Ober (2019): Agamemnon’s Cluelessness https://delong.typepad.com/files/ober-agamemnon-1.pdf
- H.N. Turteltaub (2001): Over the Wine-Dark Sea https://isbn.nu//0765344513
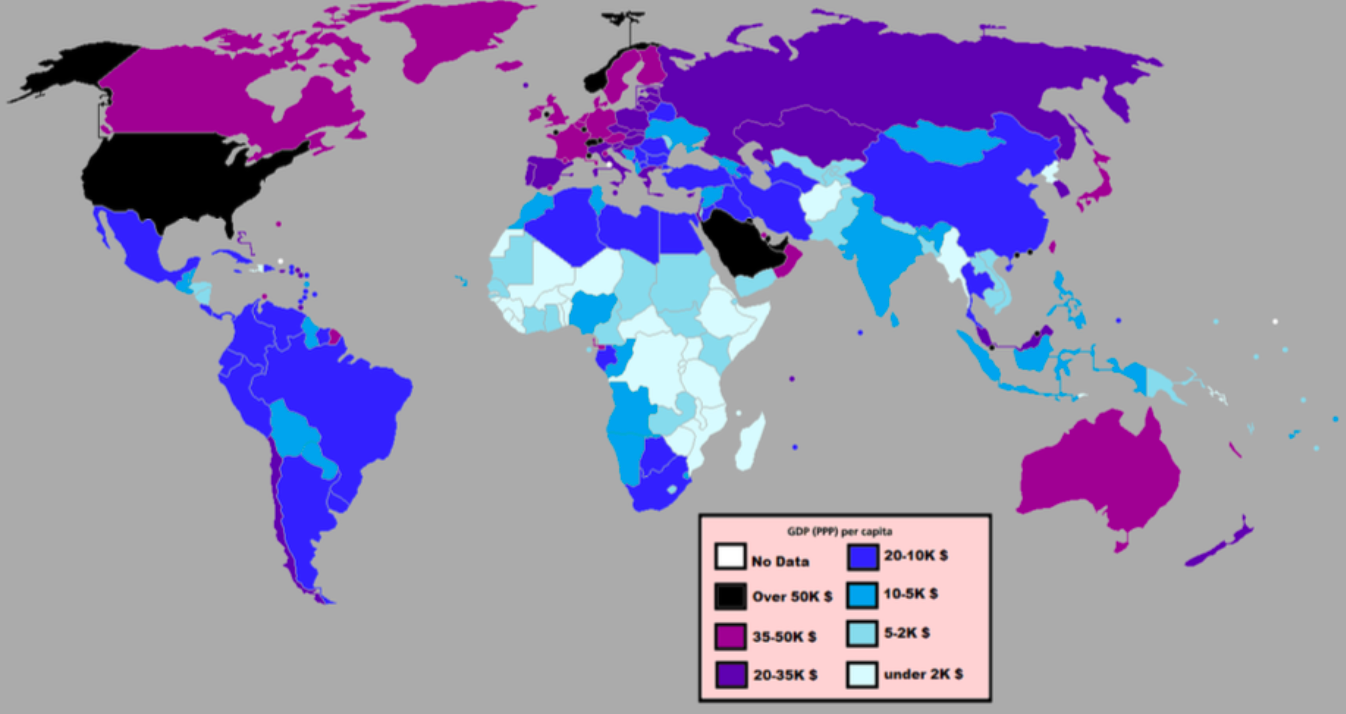
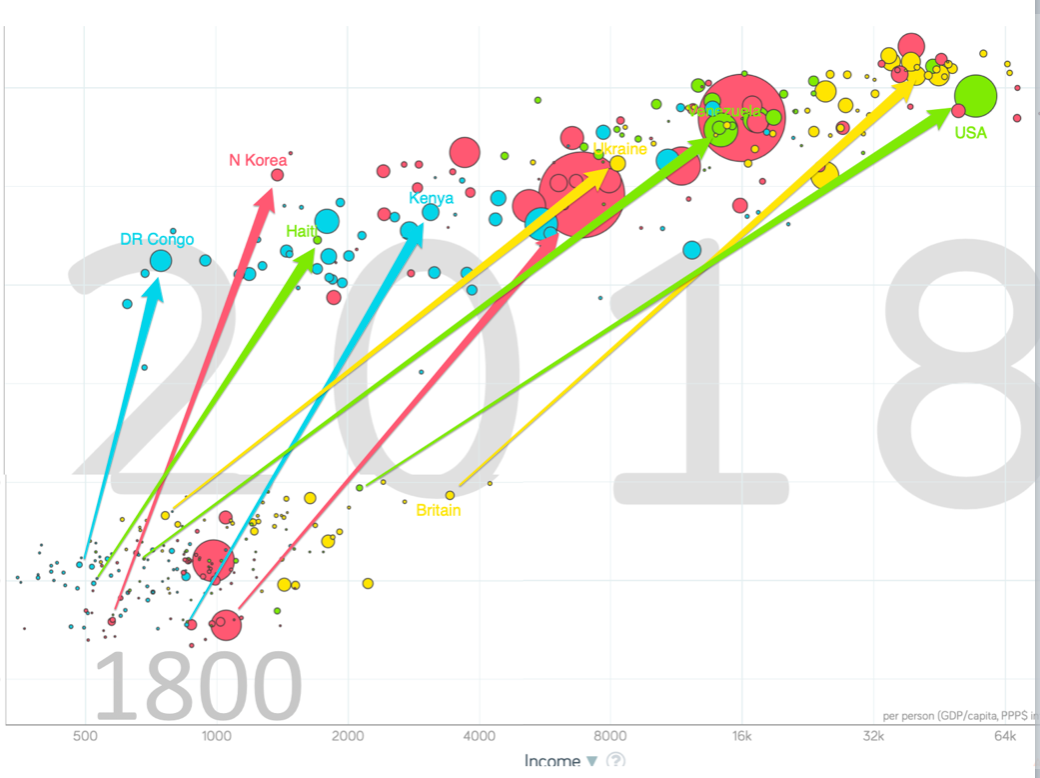
One Figure: A Great Divergence¶
- The dots start with a 3-1 spread in incomes and a 10-year spread in life expectancy.
- All the arrows go up.
- Some arrows—mostly those already to the right—go right fast.
- Other arrows go right slowly.
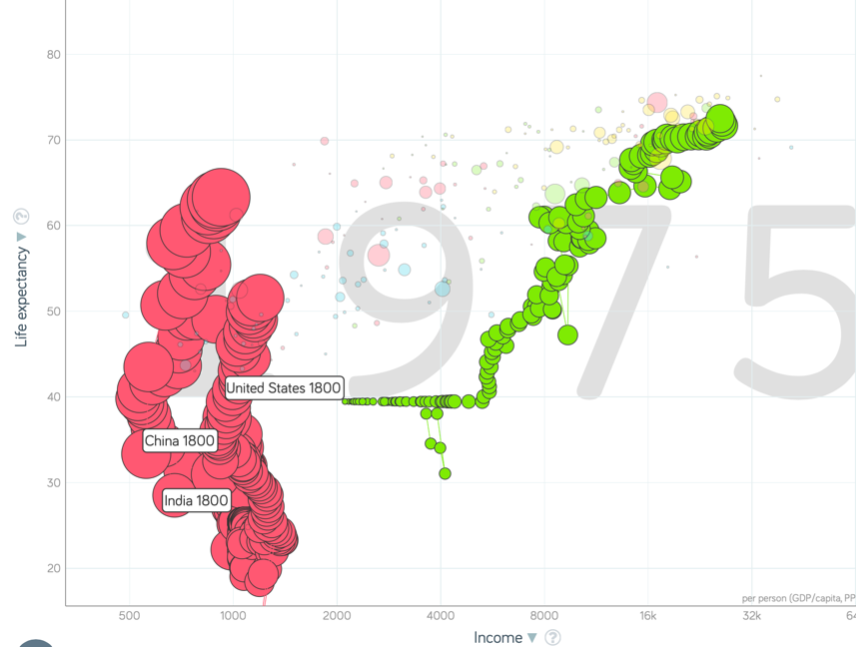
China and India and America, 1800-1975¶
- Measured living standards and productivity levels improve fourteen-fold in the United States…
- …& less than 30% in China & India…
- …in spite of economic, transport, and cultural globalization…
This is crazy!
- A “great divergence”
- Not only were China & India relatively poor in 1800, they fell further behind thereafter
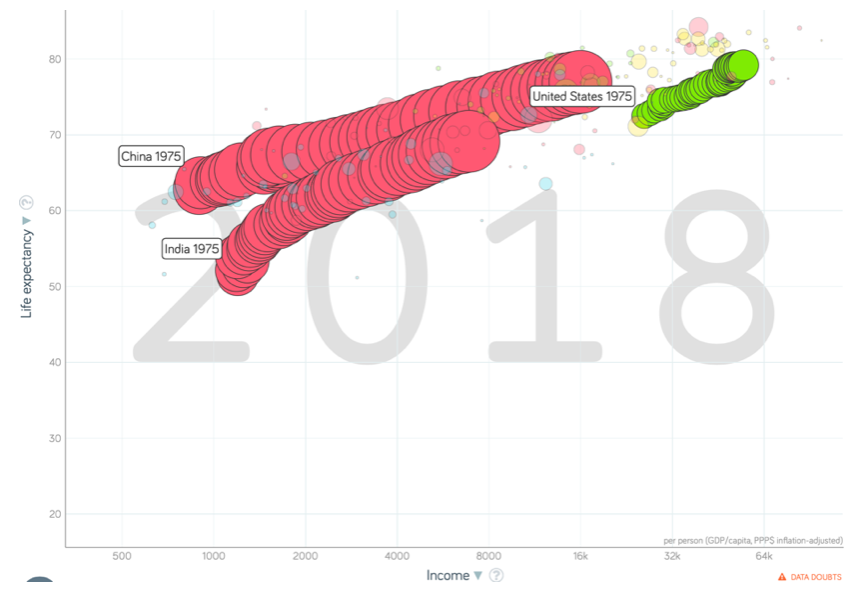
China and India and America, 1975–2018¶
- Measured living standards and productivity levels…
- …54.9/25.9 = 2.12 in America…
- …16.0/0.9 = 17.8 in China…
- …6.9/1.2 = 5.8 in India…
Subnational Inequality¶
- In Latin America, inequality across regions within countries is twice as high as inequality across countries (Acemoglu and Dell, 2010)
- About half of the differences can be statistically explained by observed human capital
- Differences also highly correlated with geography
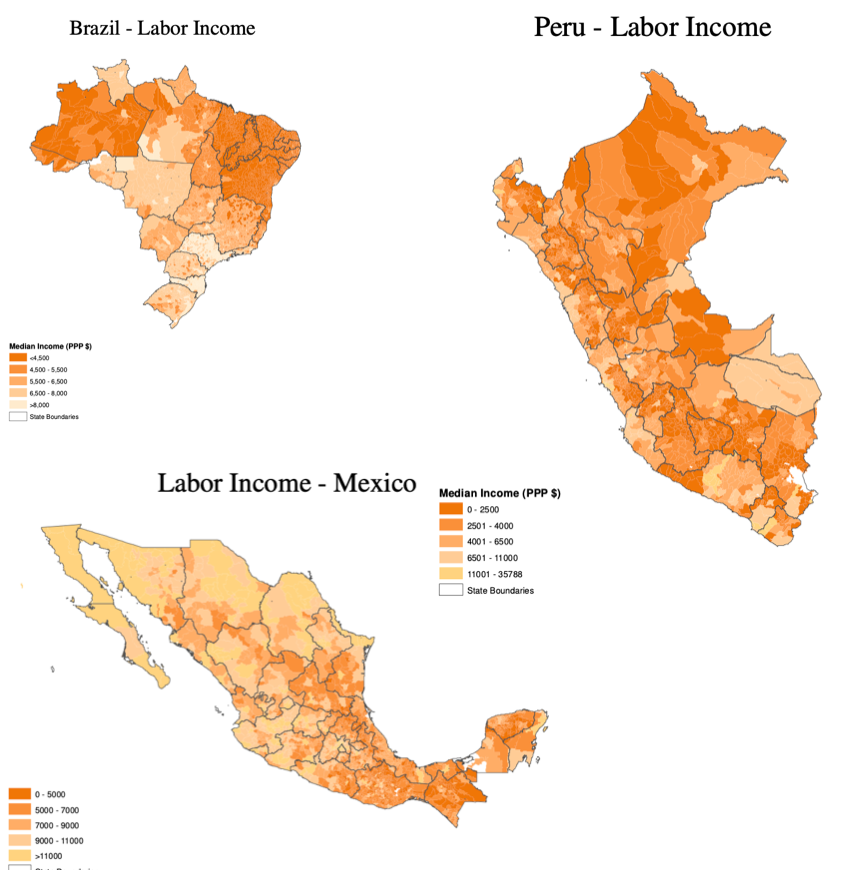
Slide taken from Melissa Dell
About the Course¶
This course examines the history of economic growth, beginning when we became “us” and continuing as far as we get. Topics covered include:
- human sociability;
- the discovery of agriculture and the domestication of animals in the Neolithic Revolution
- economic growth in ancient, Malthusian societies
- the origins and maintenance of gross inequality
- the Commercial and Industrial Revolutions
- modern economic growth
- theories and evidence about the institutional, geographic, and cultural determinants of growth: international prosperity differentials and the so-calledl "middle income trap"
- OECD convergence and East Asian miracles
- the political economy of growth and stagnation
- the stubborn persistence of poverty
Administrivia¶
Assessment: Students are graded on the basis of:
- fifteen assignments (45 points; 3 each),
- a midterm (20 points),
- in-class clicker-based quizzes & exercises (10 points),
- section exercises & participation (10 points), &
- a final (40 points)
LECTURE: TTh 09:40-11:00 Birge 50; FIRST LECTURE Jan 21
SECTIONS:
104 DIS W 08:10 Etcheverry 3119;
102 DIS W 10:10 VLSB 2070;
106 DIS Th 14:10 Dwinelle 179;
105 DIS Th 17:10 pm LeConte 385;
103 DIS M 08:10 Etcheverry 3119;
101 DIS M 10:10 VLSB 2070
COURSE WEBSITE: https://bcourses.berkeley.edu/courses/1487685
OFFICE HOURS: TBD…
Schedule
T Jan 21: Growth in Historical Perspective, Humans and Their Economies
Th Jan 23: Robert Solow's Growth Model
T Jan 28: Malthusian Perspectives
Th Jan 30: Determinants of Progress in Technology and Organization
T Feb 4: Malthusian Agricultural Economies
Th Feb 6: Civilizational "Efflorescences" and Imperial Declines
T Feb 11: Why Was Pre-Industrial Progress so Slow on Average?
Th Feb 13: Commercial Revolutions
T Feb 18: The Industrial Revolution
Th Feb 20: Why Northwest Europe?
T Feb 25: EARLY MIDTERM (Instructor Reality Check)
Th Feb 27: Modern Economic Growth
T Mar 3: U.S. Economic Ascendancy
Th Mar 5: Globalization Advances and Retreats
T Mar 10: Convergence and Its Absence
Th Mar 12: Inequality and Plutocracy
T Mar 17: The Development of Underdevelopment
Th Mar 19: Western Europe, North America, and South America
T Mar 31: Behind the Iron Curtain, and East Asian Miracles
Th Apr 2: Asia and Africa
T Apr 7: "Deep Roots" vs. Path Dependence
Th Apr 9: Growth and Fluctuations; Trade and Development, Foreign Aid
T Apr 14: Plutocracy, Kleptocracy, & Neo-Fascism
Th Apr 16: Global Warming
T Apr 21: The Pace and Meaning of Economic Growth
Th Apr 23: The Future?
T Apr 28: Conclusion
Th Apr 30: Final Review
W May 13 11:30-14:30: FINAL EXAM
Before the Course Begins…¶
Do all of the below by January 20:
- Buy your books:
- Robert C. Allen (2011): Global Economic History: A Very Short Introduction https://books.google.com/?isbn=0199596654 (HC51 .A56 2011)
- Robert C. Allen (2017): The Industrial Revolution: A Very Short Introduction https://books.google.com/?isbn=9780198706786 (HC254.5 .A664 2017)
- Christopher J. Berry (2019): Adam Smith: A Very Short Introduction https://books.google.com/?isbn=0198784457 (B1545.Z7 B47 2018)
- Partha Dasgupta (2007): Economics: A Very Short Introduction https://books.google.com/?isbn=9780192853455 (HB171 .D26 2007)
- Buy and register your iClicker; bring it to class the first day
- Do Assignment 1
Assignment 1: Read the syllabus at: ____. Using the information in the syllabus, think up a question that should be on the FAQ—the Frequently Asked Question—list for the course. Answer the question you thought up. Upload your question and answer to your account at the course on canvas at: https://bcourses.berkeley.edu/courses/1487685
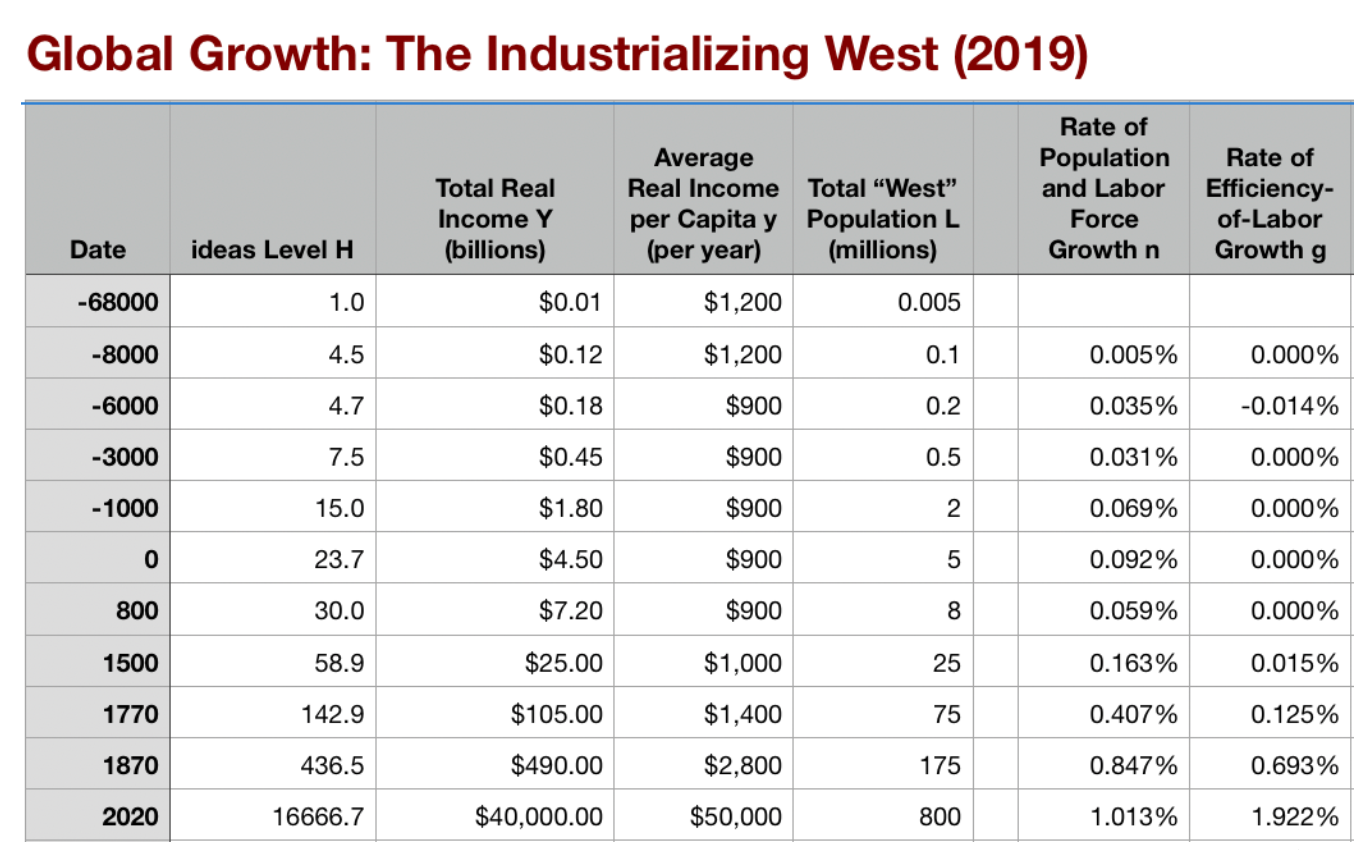
Four Major Features of the History of Economic Growth¶
- Poverty, in the pre-industrial ages, with population growth on average but with average population growth very slow
- n = 0.07%/yr; h = 0.035%/yr
- Growing prosperity, in the Industrial Revolution and the Modern Economic Growth ages
- In the MEG era: h = 2.06%/yr
- The great divergence
- Globalization
- American twentieth-century economic ascendancy
- Pre-industrial efflorescences and declines
Catch Our Breath¶

- Ask a couple of questions?
- Make a couple of comments?
- Any more readings to recommend?
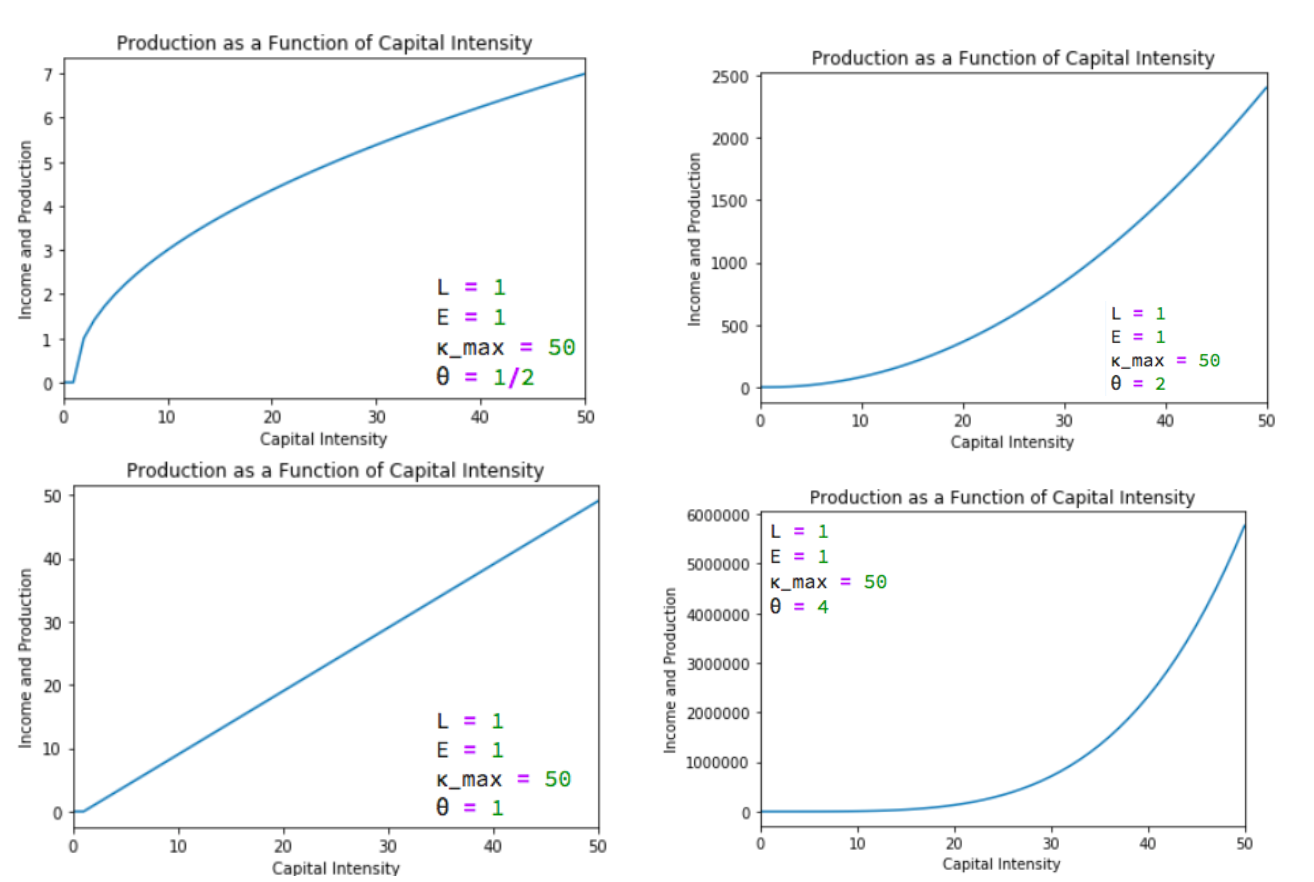
Model Basics: Production Function¶
Let's assume three things about the relationship between an economy's resources and the total output it produces and income it generates:
A proportional increase in the economy's capital intensity $ \kappa = K/Y $, measured by the capital stock divided by total production, will carry with it the same (smaller) proportional increase in income and production no matter how rich and productive the economy is. A 1% increase in capital intensity will always increase income and production by the same proportional amount.
If two economies have the same capital intensity, defined as the same capital-output ratio $ \kappa $, and have the same level of technology- and organization-driven efficiency-of-labor $ E $, then the ratio of their levels of income and output will be equal to the ratio of their labor forces $ L $.
If two economies have the same capital intensity, defined as the same capital-output ratio $ \kappa $, and have the same labor forces, then the ratio of their levels of income and output will be equal to the ratio of their technology- and organization-driven efficiencies-of-labor $ E $.
Basics: Production Notation¶
- Y: total income and production
- E: technological and organizational efficiency-of-labor
- L: labor force
- y: per-worker income and production
- κ: the capital-intensity of the economy, as measured by the capital-output ratio K/Y (Greek lower kappa)
- θ: the relative salience in economic growth of capital-intensity vis-a-vis technological and organizational progress (Greek lower theta)
- if α is the share of income received by capital under the marginal productivity theory of distribution, then α=θ/(1+θ), 1-α=1/(1+θ), θ = α/(1-α)
Basics: Production Algebra¶
Then there is one and only one equation that satisfies those three rules of thumb:
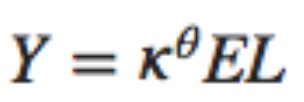
And it is also worth writing down
- a version of this equation in per-worker form, where y = Y/L
- the definition of capital intensity κ: κ= K/Y
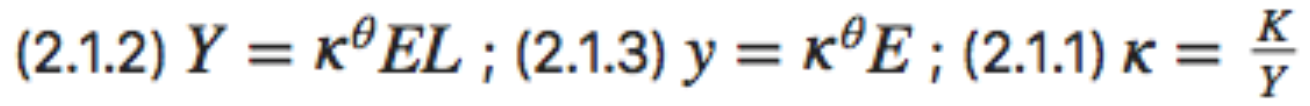
We have just done what economists typically do: take a complex situation, strip things down to some salient piece of it, and then formalize and algebraize that piece in the hope of gaining insight…
Solow Model Basics: Notes¶
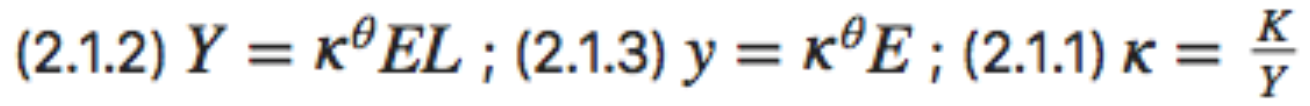
Look at:
- http://datahub.berkeley.edu/user-redirect/interact?account=braddelong&repo=long-form-drafts&branch=master&path=solow-model.ipynb
- http://datahub.berkeley.edu/user-redirect/interact?account=braddelong&repo=long-form-drafts&branch=master&path=solow-model-2-basics.ipynb
- http://datahub.berkeley.edu/user-redirect/interact?account=braddelong&repo=long-form-drafts&branch=master&path=solow-model-3-growing.ipynb
- http://datahub.berkeley.edu/user-redirect/interact?account=braddelong&repo=long-form-drafts&branch=master&path=solow-model-4-using.ipynb
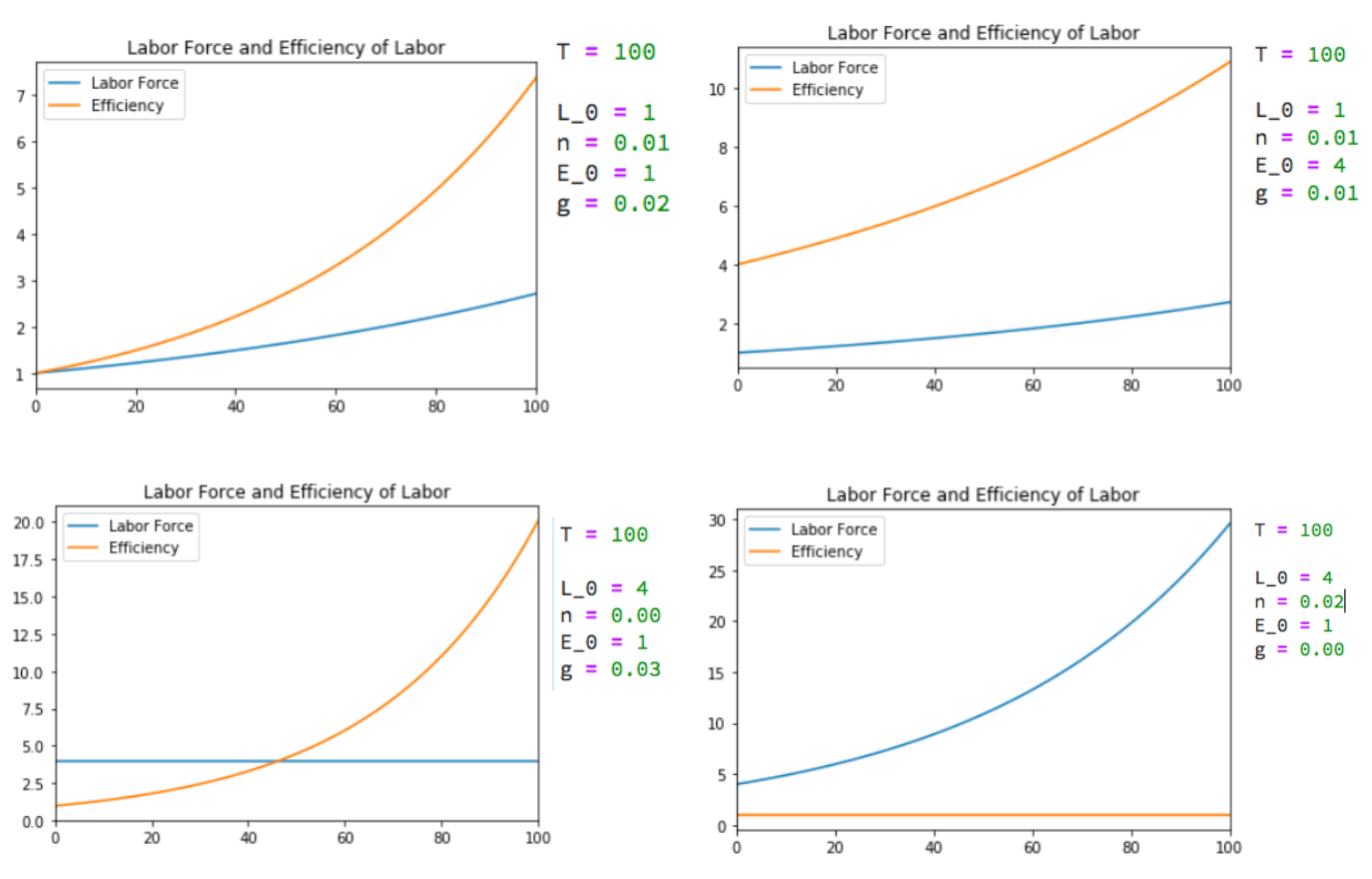
The Rest of the Model: Growth Rates¶
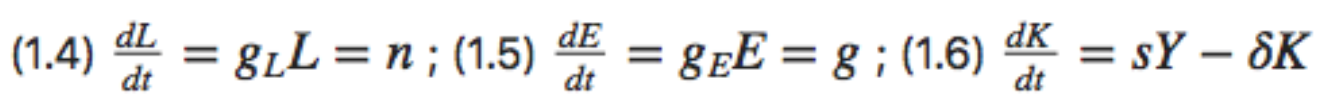
Variables change over time:
- growth of labor gL: proportional at a constant n (for now)
- growth of labor efficiency gE: proportional at a constant g (for now)
- rate of change of capital: savings minus depreciation
- What do these mean?
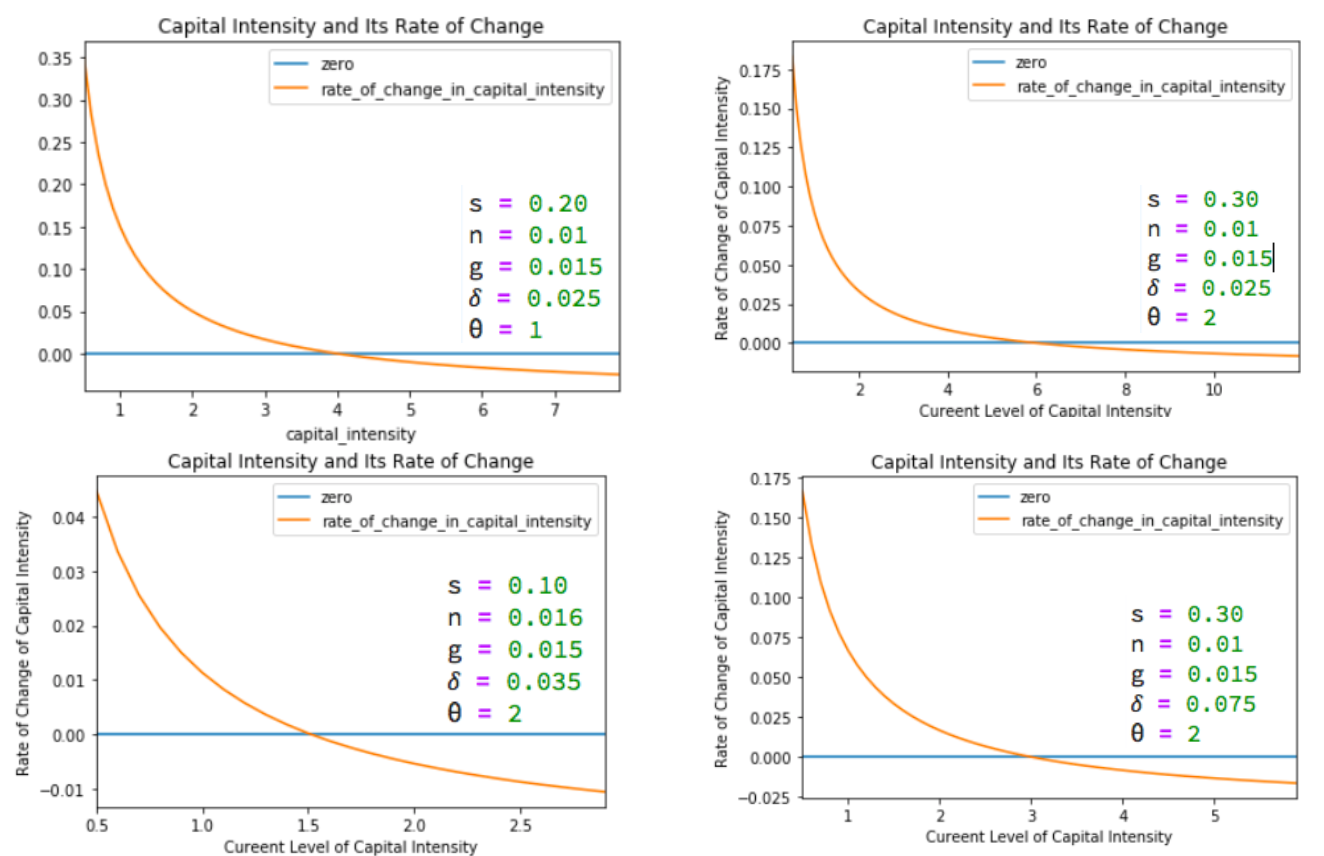
Now let’s look at the rate of change of capital-intensity κ as a function of the level of capital-intensity κ, for constant n, g, s, δ, and θ…
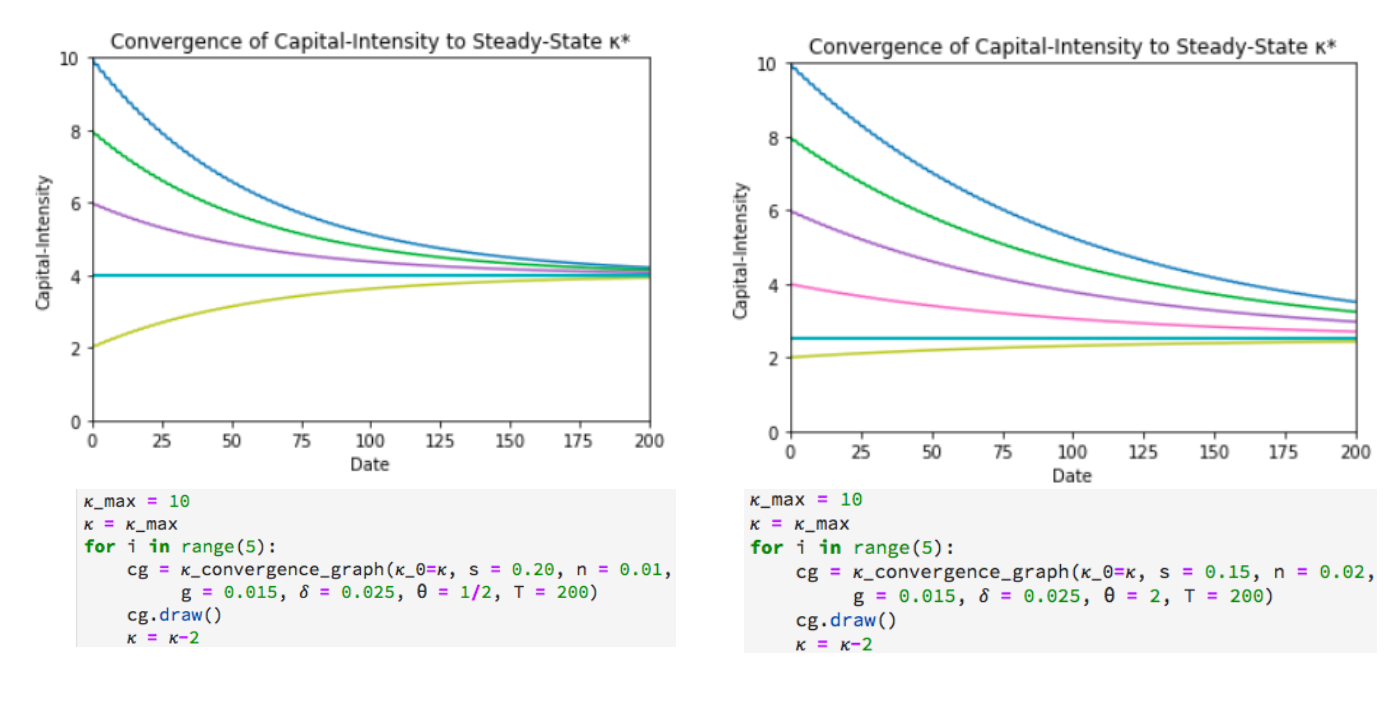
Balanced-Growth Equilibrium: Steady-State Capital Intensity κ*¶
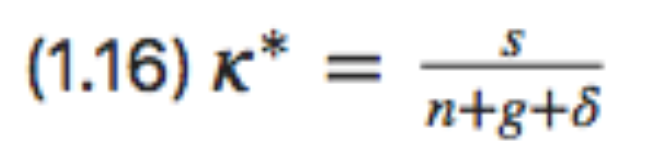
This κ* we define to be the steady-state balanced-growth equilibrium value of capital intensity κ. If κ = κ, it will be constant. If κ > κ, capital intensity will fall—and so approach κ. If κ < κ, capital intensity will rise—and so approach κ*.
Along the Balanced-Growth Path¶
Everything except κ—which is constant—grows at a constant proportional rate: either n, or g, or n+g;
- Labor force L grows at n
- Income per worker y and the efficiency of labor E grow at g
- Total income Y and the capital stock K grow at n+g
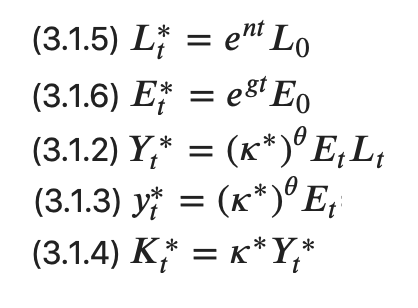
Convergence of κ to Steady-State Capital-Intensity¶
what if $ \kappa ≠ \kappa^* $? What happens then? Since $ s = \kappa^*(n+g+\delta) $, we can multiply (2.2.9) by $ \kappa $ and then rewrite it in terms of the equilibrium capital-intensity $ \kappa^* $ as:
$ \frac{d\kappa}{dt} = s/(1+\theta) - (n+g+\delta)\kappa/(1+\theta) $
$ \frac{d\kappa}{dt} = (n+g+\delta)\kappa^*/(1+\theta) - (n+g+\delta)\kappa/(1+\theta) $
$ \frac{d\kappa}{dt} = - \frac{n+g+\delta}{1+\theta} (\kappa-\kappa^*) $
$ \kappa = \kappa^* + e^{-((n+g+\delta)/(1+\theta))t}(\kappa_0 - \kappa^*) $
The Other Variables of the Model Are Then...¶
$ E_t = e^{gt}E_0 $
$ L_t = e^{nt}L_0 $
$ Y_t = \left(\kappa_t \right)^\theta E_t L_t$
$ y_t = \left(\kappa_t \right)^\theta E_t$
$ K_t = \kappa_t Y_t $
Catch Our Breath¶

- Ask a couple of questions?
- Make a couple of comments?
- Any more readings to recommend?
1.2. Theory: The Malthus-Solow Economic Growth Model¶
Brad DeLong Department of Economics and Blum Center, U.C. Berkeley; and WCEG last revised: 2020-01–12
Original course by Melissa Dell (Harvard Econ 1342), revised by Brad DeLong, research assistance by Anish Biligiri