A Statistical Analysis of the Virginia Smart Scale Scoring Methodology¶

September 17, 2018¶

Christopher Garcia, Ph.D., Mukesh Srivastava, D.B.A.¶

University of Mary Washington, Center for Business Research¶

Executive Summary¶

The Smart Scale methodology is intended to provide an objective, transparent, and consistent way to evaluate and compare the benefits of competing transportation projects in Virginia. This study provides a statistical analysis of a set of 404 Smart Scale Round 2 projects scored using the Smart Scale methodology. The study's first goal was to provide a basic characterization of the Smart Scale score distribution across different project features, while the second goal was to answer the following two questions:

Was the Smart Scale methodology applied consistently across all projects?
If Accessibility (a key concern for the Fredericksburg area) was prioritized in Smart Scale score calculation for area types A and D (the area types where Fredericksburg projects occur), how would this impact the competitiveness of Fredericksburg-based projects?

To answer the first question, the Smart Scale scores were independently calculated for each project using the methodology prescribed in the November 2017 Smart Scale Technical Guide. These scores were then compared to the project scores assigned by the state. There was no discrepancy between the calculated scores and scores assigned by the state, indicating that the Smart Scale methodology was consistently applied accross all projects.

To answer the second question, two alternative scenarios were used which both increased the importance of Accessibility in the scoring calculation. All projects were scored according to the methodology defined in each scenario, and the percentile rankings of the Fredericksburg scores under each alternative scenario were compared to that obtained by the current methodology. There were small increases in the percentile rankings of some Fredericksburg project scores under one of the alternative scenarios when compared to the current scoring methodology. This suggests that the full impact of some Fredericksburg-based projects may be underestimated under the current Smart Scale methodology and, depending on the cut score, these projects may be edged out of funding accordingly.

I. Introduction¶

The Virginia Smart Scale methodology was finalized in November 2017 in order to provide an objective scoring system for the state's transportation projects competing for funding. The complete technical specification of the Smart Scale methodology can be found in the November 2017 technical guide, found here: http://vasmartscale.org/documents/20171115/ss_technical_guide_nov13_2017.pdf.

The purpose of this analysis is 1) to provide a descriptive statistical characterization of recently funded projects, 2) to independently assess whether the Smart Scale scores (abbreviated by SSS hereafter) assigned to these projects were consistent with the Smart Scale methodology as specified in the technical guide, and 3) to determine how increasing the emphasis on Accessibility (which is a major concern to the Fredericksburg area) in the SSS calculation methodology would impact the competitiveness of Fredericksburg-based projects. This analysis uses a dataset provided by the Fredericksburg Area Metropolitan Planning Organization (FAMPO), containing data on 404 Smart Scale Round 2 projects. This analysis also uses the R statistical computing environment within a Jupyter notebook. This allows the analysis to be both explained as well as executed. It furthermore enables complete transparancy of the analytical methodology and code used in its execution. This removes any ambiguity and also guarantees reproducibility of the results.

II. Data Inspection and Preparation¶

The data was provided in a Microsoft Excel spreadsheet. This spreadsheet was first converted to a CSV file (ss-data.csv) and then a number of transformation processes were applied to clean and scale the data as well as to impute missing values. To begin, we first import several libraries which will be used later on and also define several functions which will be used in the data preparation:

In [1]:

# Turn off verbose output messages.
options(warn=0)

# Include all libraries that will be used in this notebook's code
library(ggplot2)
library(gridExtra)

# Given a vector, a vector of original values, and a corresponding vector of 
# replacement values, apply the replacements and return the transformed vector.
recode <- function(vec, from.vals, to.vals) {
    f = function(v) {
        for(i in 1:length(from.vals)) {
            if(v == from.vals[i]) { return(to.vals[i]) }
        }
        return(v)
    }
    return(sapply(as.vector(vec), f))
}

# Function for imputing mean of a vector to its missing values.
impute.mean <- function(vec) {
    vec[is.na(vec)] = mean(vec, na.rm=TRUE)
    vec
}

# Function for imputing value of 0 to each missing value in the vector.
impute.0 <- function(vec) {
    vec[is.na(vec)] = 0
    vec
}

Next we read in the dataset and inspect the first few rows of data:

In [2]:

data <- read.csv('ss-data.csv')
head(data)

App.Id	Area.Type	District	Organization.Name	Project.Title	Statewide.High.Priority	District.Grant	Throughput.Score	Delay.Score	Crash.Frequency.Score	...	Travel.Time.Reliability.Score	Land.Use.Score	Project.Benefit.Score	Total.Project	Score.Divided.by.Total.Cost	SMART.SCALE.Request	SMART.SCALE.Score	Benefit.Rank	State.Rank	District.Rank
1414	A	NOVA	Northern Virginia Transportation Commission	VRE Fredericksburg Line Capacity Expansion	x		17.69	87.66	100	...	-	64.016	64.236	216034920	2.973	92636120	6.934	1	109	16
1057	A	Hampton Roads	Hampton Roads Transportation Planning Organization	I-64 Southside Widening and High Rise Bridge - Phase 1	x		100	88.96	45.16	...	29.044	10.464	62.042	600000000	1.034	100000000	6.204	2	120	22
1090	A	Hampton Roads	Hampton Roads Transportation Planning Organization	I-64/I-264 Interchange Improvements	x		60.61	53.86	-	...	24.245	31.671	48.747	350091800	1.392	50000000	9.749	3	79	18
1293	A	NOVA	Prince William County	Route 234 At Balls Ford Intrchng and Rel/Widen Balls Ford Rd	x	x	65.48	100	15.61	...	1.05	-	41.289	126027000	3.276	124027000	3.329	4	170	30
1249	A	NOVA	Fairfax County	VA 286 - Popes Head Road Interchange	x	x	61.09	54.17	8.22	...	0.118	-	37.194	64303070	5.784	50558370	7.357	5	101	14
1240	A	NOVA	Loudoun County	Loudoun County Parkway (Shellhorn Road to US Route 50)	x	x	45.27	69.78	5.43	...	1.6	16.364	33.732	112053000	3.01	112053000	3.01	6	179	32

In the technical guide (Table 4.2, p. 36) there are six major factors used to compute the Smart Scale score, which are themselves calculated from more basic measurements:

Congestion Mitigation
Economic Development
Accessibility
Safety
Environmental Quality
Land Use

Of these six factors only Land Use is directly given in the dataset. All other major metrics are calculated from their basic constituent measurements as specified on pages 27-31. Within the data there are four area types: A, B, C, and D. Each of these area types has a unique factor weighting used in calculating in its Smart Scale Score. These weightings are specified for each area in Table 4.2 on page 36 within the technical guide. It is noted that for areas C and D, the Land Use factor is not used (or equivalently, carries 0% weight). Upon inspection of the whole dataset it was apparent that this was represented by empty cells for projects falling within these area types. Accordingly, all such Land Use values are set to 0. By this precedent it also is taken that all empty cells in numeric columns correspond to zero. Accordingly, a value of zero is imputed to all empty cells.

Based upon this, the following basic transformations are made to the data prior to analysis:

All columns with present/absent markers (x and no x) are recoded to 1 and 0, respectively. This converts them into a numeric equivalent (called binarization).
All empty cells in basic constituent measurement columns (which are used in calculating the factors) and other numeric values are changed to zero.
All empty cells in the Land Use column are changed to zero.

Additionally, prior to imputing zeros to empty cells we inspect the percentages of empty cells in the numeric colums. All this is done as follows:

In [3]:

# Clean and recode numeric columns.
numeric.columns <- colnames(data)[8:ncol(data)]
for(col in numeric.columns) {
    data[[col]] <- suppressWarnings(as.numeric(as.character(data[[col]]))) 
}

imputer.f <- impute.0 # Missing value imputation function - can change if needed

# Impute missing values to component scores and print out the percent missing in each column
missing.ind <- 1
missing.perc <- c()
missing.titles <- c()
for(i in 8:ncol(data)) {
    missing.titles[missing.ind] <- colnames(data)[i]
    missing.perc[missing.ind] <- round(100*(1 - (length(sort(data[[i]]))/nrow(data))), 2) 
    data[[i]] <- imputer.f(data[[i]])
    missing.ind <- missing.ind + 1
}

# Properly binarize binary columns.
data$Statewide.High.Priority <- as.numeric(sapply(data$Statewide.High.Priority, function(x){if(x == 'x') return(1); return(0);}))
data$District.Grant <- as.numeric(sapply(data$District.Grant, function(x){if(x == 'x') return(1); return(0);}))

# Display summary of missing values
data.frame(Column_Name=missing.titles, Percent_Missing_Values=missing.perc)

Column_Name	Percent_Missing_Values
Throughput.Score	30.94
Delay.Score	25.99
Crash.Frequency.Score	17.08
Crash.Rate.Score	19.80
Access.to.Jobs	33.91
Disadvantaged.Access.to.Jobs	33.91
Multimodal.Access.Score	41.34
Air.Quality.Score	34.16
Enviro.Impact.Score	0.99
Econ.Dev.Support.Score	37.87
Intermodal.Access.Score	60.15
Travel.Time.Reliability.Score	31.19
Land.Use.Score	56.44
Project.Benefit.Score	0.74
Total.Project	0.00
Score.Divided.by.Total.Cost	0.74
SMART.SCALE.Request	0.00
SMART.SCALE.Score	0.74
Benefit.Rank	0.00
State.Rank	0.00
District.Rank	0.00

In the output above, the percentage of missing values in the key numeric columns ranges from 0% to 74%. We note that 74% of rows are missing a SMART.SCALE.Score and Project.Benefit.Score, meaning that only 26% of the projects have a Project Benefit Score and Smart Scale Score assigned - which is interpreted as only 26% of the projects having a Project Benefit Score and Smart Scale Score greater than zero.

III. Data Exploration¶

In this section we explore the data further using descriptive statistics to provide several characterizations. We begin by looking at the overall distribution of Smart Scale Scores (SSS) ordered from least to greatest:

In [4]:

sssr <- data[order(data$SMART.SCALE.Score),]
sssr <- cbind(sssr, data.frame(ind=1:nrow(data)))
ggplot(sssr, aes(x=ind, y=SMART.SCALE.Score, shape=Area.Type, color=Area.Type)) +
    geom_point() +
    labs(x='Rank', y='Smart Scale Score', 
         title='Fig. 1: Smart Scale Scores (Ordered)')

In Fig. 1 above, the SSS's appear to follow a power law, with a long tail on the left and a relatively small number of projects having extreme scores. The distribution of scores clearly does not follow a linear pattern. Below we inspect the percentile thresholds from this sample by SSS:

In [5]:

sss.ord <- sort(data$SMART.SCALE.Score)
percentiles <- c(0.05, 0.1, 0.25, 0.5, 0.75, 0.9, 0.95)
cut.scores <- sapply(percentiles, function(p){sss.ord[ceiling(p * nrow(data))]})
percentile.cutoffs <- data.frame(Percentile=100 * percentiles, Score=cut.scores)
percentile.cutoffs

Percentile	Score
5	0.149
10	0.283
25	0.737
50	2.301
75	7.347
90	25.141
95	44.623

Because only a small number of projects exceed a SSS of 30, we will truncate all subsequent exploratory visualizations at 30 to best enable the majority variation to be seen clearly.

3.1 Descriptive Statistics for Majority (Lower-Scoring) Projects (SSS < 30)¶

To drill down further, we look at the distribution of Smart Scale Scores by area type and district. We begin with area type, looking at the number of projects within each of the four area types together with their average and median smart scale scores:

In [6]:

dt1 <- data.frame(table(data$Area.Type))
m1 <- data.frame(aggregate(data$SMART.SCALE.Score ~ data$Area.Type, FUN=mean))
mm1 <- data.frame(aggregate(data$SMART.SCALE.Score ~ data$Area.Type, FUN=median))
dt1 <- cbind(dt1, m1$data.SMART.SCALE.Score, mm1$data.SMART.SCALE.Score)
colnames(dt1) <- c('Area_Type', 'Num_Projects', 'Mean_Smart_Scale_Score', 'Median_Smart_Scale_Score')
dt1

Area_Type	Num_Projects	Mean_Smart_Scale_Score	Median_Smart_Scale_Score
A	114	16.287246	2.9795
B	88	8.776795	4.3685
C	86	6.257140	1.9760
D	116	7.978250	1.4635

By comparing the mean SSS to the medians, it is apparant that the few high-scoring projects significantly inflate the means. Below we look more closely at the spread of the SSS by area type (truncated at 30, as discussed above):

In [7]:

boxplot(SMART.SCALE.Score~Area.Type,data=data, main="Fig. 2: Smart Scale Score Distribution by Area Type",
        xlab="Area Type", ylab="Smart Scale Score", ylim=c(0, 30), col="yellow")

In Fig. 2 above, area type A has the greatest amount of variance while area type D has the least. Area types C and D have similar distribution profiles, with area type D having the lowest overall median.

Below we shift our perspective to look at SSS with respect to district. We begin with a basic summarization of scores by district:

In [8]:

dt2 <- data.frame(table(data$District))
m2 <- data.frame(aggregate(data$SMART.SCALE.Score ~ data$District, FUN=mean))
mm2 <- data.frame(aggregate(data$SMART.SCALE.Score ~ data$District, FUN=median))
dt2 <- cbind(dt2, m2$data.SMART.SCALE.Score, mm2$data.SMART.SCALE.Score)
colnames(dt2) <- c('District', 'Num_Projects', 'Mean_Smart_Scale_Score', 'Median_Smart_Scale_Score')
dt2

District	Num_Projects	Mean_Smart_Scale_Score	Median_Smart_Scale_Score
Bristol	42	1.160738	0.4695
Culpeper	35	3.597029	2.1690
Fredericksburg	25	8.902320	1.8640
Hampton Roads	52	23.536212	2.0735
Lynchburg	28	9.429893	1.7990
NOVA	58	11.844241	3.3630
Richmond	72	7.878069	3.2880
Salem	50	10.277980	2.5410
Staunton	42	10.463905	2.7075

In a manner similar to above, we see the extreme high-scoring projects inflating the means. In Fig. 3 below the distribution of scores by district is shown.

In [9]:

boxplot(SMART.SCALE.Score~District,data=data, main="Fig. 3: Smart Scale Score Distribution by District",
        xlab="District", ylab="Smart Scale Score", ylim=c(0, 30), col="yellow", cex.axis=0.4)

In Fig. 3 the Hampton Roads district has significantly more variance than all other districts, while NOVA and Richmond have the highest medians scores.

3.2 Descriptive Statistics for Minority High-Scoring Projects (SSS > 30)¶

Up to now the exploration has been focused on the majority of projects which tend toward the lower range of SSS. We turn our attention to the scores falling on the far right of Fig. 1 ranging from 30 and above. We first tabulate the number of projects falling in this range by area type:

In [10]:

high.ss <- subset(data, SMART.SCALE.Score >= 30)
dt3 <- data.frame(table(high.ss$Area.Type))
m3 <- data.frame(aggregate(high.ss$SMART.SCALE.Score ~ high.ss$Area.Type, FUN=mean))
mm3 <- data.frame(aggregate(high.ss$SMART.SCALE.Score ~ high.ss$Area.Type, FUN=median))
dt3 <- cbind(dt3, m3$high.ss.SMART.SCALE.Score, mm3$high.ss.SMART.SCALE.Score)
colnames(dt3) <- c('Area_Type', 'Num_Projects', 'Mean_Smart_Scale_Score', 'Median_Smart_Scale_Score')
dt3

Area_Type	Num_Projects	Mean_Smart_Scale_Score	Median_Smart_Scale_Score
A	13	105.97615	61.1800
B	4	58.23500	47.1480
C	6	47.45583	41.3365
D	10	59.80840	62.2070

We see above that area types A and D have the majority of these high-scoring projects. A similar breakdown by district is shown below.

In [11]:

dt4 <- data.frame(District=unique(data$District))
dt4 <- merge(dt4, data.frame(table(high.ss$District)), by.x='District', by.y='Var1', all.x=TRUE)
m4 <- data.frame(aggregate(high.ss$SMART.SCALE.Score ~ high.ss$District, FUN=mean))
dt4 <- merge(dt4, m4, by.x='District', by.y='high.ss.District', all.x=TRUE)
mm4 <- data.frame(aggregate(high.ss$SMART.SCALE.Score ~ high.ss$District, FUN=median))
dt4 <- merge(dt4, mm4, by.x='District', by.y='high.ss.District', all.x=TRUE)
colnames(dt4) <- c('District', 'Num_Projects', 'Mean_Smart_Scale_Score', 'Median_Smart_Scale_Score')
dt4

District	Num_Projects	Mean_Smart_Scale_Score	Median_Smart_Scale_Score
Bristol	0	NA	NA
Culpeper	0	NA	NA
Fredericksburg	2	57.72750	57.7275
Hampton Roads	11	95.42873	59.8350
Lynchburg	3	67.47600	79.6260
NOVA	4	108.68375	86.2600
Richmond	4	50.86100	40.4150
Salem	4	58.85550	48.1505
Staunton	5	50.44980	42.0710

Because there are so few projects at this score range, we will omit further drill-down to look at actual score distributions.

IV. Examination of Scoring Consistency¶

An important aspect of this analysis is to see if the scoring methodology as specified in the technical guide was applied consistently to the projects. As previously discussed, in the technical guide (Table 4.2, p. 36) there are six major factors used to compute the Smart Scale score which are themselves calculated from more basic measurements:

Congestion Mitigation
Economic Development
Accessibility
Safety
Environmental Quality
Land Use

Of these six factors only Land Use is directly given in the dataset. All other major metrics are calculated from their basic constituent measurements as specified on pages 27-31. Within the data there are four area types: A, B, C, and D. Each of these area types has a unique factor weighting that results in its Smart Scale Score. These weightings are specified for each area in Table 4.2 on page 36 within the technical guide. It is noted that for areas C and D, the Land Use factor is not used (or equivalently, carries 0% weight).

The examination of scoring consistency will be accomplished by independently calculating the SSS score of each project according to the specifications in the technical guide. These independently-calculated scores will then be compared to the scores provided in the dataset by fitting a linear regression, and the degree of fit will be used to determine the degree of consistency.

4.1 Comparing Assigned Smart Scale Scores to Scores Calculated According to the Technical Guide¶

Pages 37-40 of the technical guide specify how to calculate the final smart scale score, and in this section we implement these calculations in an attempt to replicate the assigned Smart Scale Scores. In the dataset all basic measurements needed for each factor weight calculation are present except for those pertaining to the Land Use factor. Instead, a Land Use factor score is provided. All steps in the calculation process are summarized in Table 4.6 on p. 40 of the technical guide.

4.1.1 Replicating the Technical Guide Calculations on the Data¶

The Smart Scale Score calculations specified technical guide are replicated on the dataset below:

In [12]:

#------ Step 1: Normalization of Measure Weights
measure.cols <- c('Throughput.Score', 'Delay.Score',
                  'Econ.Dev.Support.Score', 'Intermodal.Access.Score', 'Travel.Time.Reliability.Score',
                  'Access.to.Jobs', 'Disadvantaged.Access.to.Jobs', 'Multimodal.Access.Score',
                  'Crash.Frequency.Score', 'Crash.Rate.Score',
                  'Air.Quality.Score', 'Enviro.Impact.Score')
for(i in measure.cols) {data[[i]] <- 100 * data[[i]] / max(data[[i]])}

#------ Step 2: Apply Measure Weights
# For a given data frame, a set of weights, and a set of selected columns, this function returns a new
# vector corresponding to the weighted averages of the columns.
weighted.column.average <- function(data.frame, weight.vec, selected.columns) {
  v <- 0 
  for(i in 1:length(weight.vec)) {
    v <- v + (weight.vec[i] * data.frame[[selected.columns[i]]])
  }
  v
}

# Calculate the composite factor scores (except Land Use, which is already given in the data) from 
# component scores according to the Smart Scale November 2017 technical guide, p. 40.
data$Congestion.Score <- weighted.column.average(data, c(0.5, 0.5), c('Throughput.Score', 'Delay.Score'))
data$Economic.Score <- weighted.column.average(data, c(0.6, 0.2, 0.2), 
                                               c('Econ.Dev.Support.Score', 'Intermodal.Access.Score', 
                                                 'Travel.Time.Reliability.Score'))
data$Accessibility.Score <- weighted.column.average(data, c(0.6, 0.2, 0.2), 
                                                    c('Access.to.Jobs', 'Disadvantaged.Access.to.Jobs', 
                                                      'Multimodal.Access.Score'))
data$Safety.Score <- weighted.column.average(data, c(0.5, 0.5), c('Crash.Frequency.Score', 'Crash.Rate.Score'))
data$Environmental.Score <- weighted.column.average(data, c(0.5, 0.5), c('Air.Quality.Score', 'Enviro.Impact.Score'))
# Land use score already in data - no component scores listed.

#------ Step 3: Apply Factor Weights
# Given a dataframe with calculated factor scores, this function computes the project value according to 
# Table 4.2, p.36 of the technical guide.
calc.proj.value <- function(dataset, weight.a=c(0.45, 0.05, 0.15, 0.05, 0.1, 0.2),
                                     weight.b=c(0.15, 0.2, 0.25, 0.2, 0.1, 0.1),
                                     weight.c=c(0.15, 0.25, 0.25, 0.25, 0.1),
                                     weight.d=c(0.10, 0.35, 0.15, 0.3, 0.1)) {
  factor.cols.ab <- c('Congestion.Score', 'Economic.Score', 'Accessibility.Score', 'Safety.Score',
                      'Environmental.Score', 'Land.Use.Score')
  factor.cols.cd <- c('Congestion.Score', 'Economic.Score', 'Accessibility.Score', 'Safety.Score',
                      'Environmental.Score')
  sa <- weighted.column.average(dataset, weight.a, factor.cols.ab)
  sb <- weighted.column.average(dataset, weight.b, factor.cols.ab)
  sc <- weighted.column.average(dataset, weight.c, factor.cols.cd)
  sd <- weighted.column.average(dataset, weight.d, factor.cols.cd)
  scores <- c()
  for(i in 1:nrow(dataset)) {
    if(dataset[i, 'Area.Type'] == 'A') {scores[i] <- sa[i]}
    else if(dataset[i, 'Area.Type'] == 'B') {scores[i] <- sb[i]}
    else if(dataset[i, 'Area.Type'] == 'C') {scores[i] <- sc[i]}
    else {scores[i] <- sd[i]}
  }
  scores
}

# Add a new column to data with our calculated project benefit scores.
data['Calc.Project.Benefit.Score'] <- calc.proj.value(data)

#------ Step 4: Divide Project Benefit by Smart Scale Funded Cost. 
data['Calc.SMART.SCALE.Score'] <- 1e7 * data[['Calc.Project.Benefit.Score']] / data[['SMART.SCALE.Request']]

4.1.2 Comparing the Calculated versus Assigned Smart Scale Scores¶

In order to assess the whether the calculation methodology as specified in the technical guide was applied consistently across the projects, we will use a linear regression model that fits the assigned SSS to the calculated SSS. If the two scores are perfectly consistent across the projects then they will fall perfectly along the line of best fit. Since the factor weightings differ across area type, we assess the fit for each of the four area types below.

In [13]:

# Given a dataset this function builds a scatterplot with the linear regression trend line.
ss.scatter.plot <- function(dataset, title='Calculated vs. Assigned Smart Scale Scores', title.size=22) {
  ggplot(data=dataset,
         aes(x=Calc.SMART.SCALE.Score, y=SMART.SCALE.Score)) +
    geom_point() + 
    geom_smooth(method=lm) +
    labs(x='Calculated Smart Scale Score', y='Assigned Smart Scale Score', 
         title=title) +
    theme(plot.title = element_text(size=title.size))
}

# Build the linear models for each area type.
a.lm <- lm(SMART.SCALE.Score ~ Calc.SMART.SCALE.Score, data=subset(data, Area.Type == 'A'))
b.lm <- lm(SMART.SCALE.Score ~ Calc.SMART.SCALE.Score, data=subset(data, Area.Type == 'B'))
c.lm <- lm(SMART.SCALE.Score ~ Calc.SMART.SCALE.Score, data=subset(data, Area.Type == 'C'))
d.lm <- lm(SMART.SCALE.Score ~ Calc.SMART.SCALE.Score, data=subset(data, Area.Type == 'D'))

# Build plots for each of the four area types.
sp.a <- ss.scatter.plot(subset(data, Area.Type == 'A'), 
                        paste('Fig. 4A: Area Type A (R-Squared = ', round(summary(a.lm)$r.squared, 3), ')', sep=''), 11)
sp.b <- ss.scatter.plot(subset(data, Area.Type == 'B'), 
                        paste('Fig. 4B: Area Type B (R-Squared = ', round(summary(b.lm)$r.squared, 3), ')', sep=''), 11)
sp.c <- ss.scatter.plot(subset(data, Area.Type == 'C'), 
                        paste('Fig. 4C: Area Type C (R-Squared = ', round(summary(c.lm)$r.squared, 3), ')', sep=''), 11)
sp.d <- ss.scatter.plot(subset(data, Area.Type == 'D'), 
                        paste('Fig. 4D: Area Type D (R-Squared = ', round(summary(d.lm)$r.squared, 3), ')', sep=''), 11)

# Display the four plots within a single grid.
grid.arrange(sp.a, sp.b, sp.c, sp.d, nrow=2)

The R-squared values are nearly 1.0 for all area types, indicating a near perfect correspondance between calculated and assigned scores. This indicates that the Smart Scale methodology was consistenly applied accross projects.

4.2 Synopsis and Conclusions¶

In this section we examined whether the Smart Scale scoring methodology was consistently applied to the projects in the dataset by independently implementing the calculation method specified in the technical guide and comparing the results to the assigned Smart Scale scores. The degree of agreement was determined using linear regression fitting the assigned score to the calculated score. The results suggest that the methodology was applied consistently and in conformance to the November 2017 technical guide.

V. The Effect of Prioritizing Accessibility on Fredericksburg Projects¶

The Fredericksburg area is unique in that a large percentage of its workforce commutes outside the region. Accordingly, in this section we will examine the effect of two hypothetical scenarios which give priority to the Accessibility factor in calculating the Smart Scale Scores of projects in the Fredericksburg district. Specifically, three scenarios will be compared: 1) the current SSS calculation method as specified in the November 2017 technical guide, 2) a SSS calculation method that give priority to the Accessibility factor, and 3) a SSS calculation method that gives priority to the Accessibility factor while simultaneously increasing the Access to Jobs metric by a factor of 1.5 for projects in the Fredericksburg region (explained further below). In each case we will look at the number of Fredericksburg projects appearing in different percentile ranges by Smart Scale Score. These scenarios will be referred to as 1, 2, and 3, respectively.

The Accessibility factor is composed of the weighted average of three measures: 1) Access to Jobs (60%), 2) Access to Jobs for Disadvantaged Populations (20%), and 3) Access to Multimodal Choices (20%) (Nov. 2017 Technical Guide, p. 29). In Appendix C of the technical guide, the "Access to Jobs" measure is defined as the average increase in accessibility to jobs within 45 minutes. According to a recent study, approximately 37% of the workforce in Fredericksburg commutes outside the region, with more than 50% of these commuters commuting for an hour or more [1]. The vast majority of these commute to Northern VA, DC, Richmond, and Maryland - nearly all of which are beyond 45 minutes. A more appropriate measure for Fredericksburg would thus be to use a 75-minute reach or greater. Since there is no way to know how this reach would change the Access to Jobs without the GIS tool, an estimated increase of 1.5 times the current numbers will be used in scenario 3.

To begin, we inspect the number of Fredericksburg projects in different areas:

In [14]:

fb <- subset(data, District=='Fredericksburg')
dt5 <- data.frame(table(fb$Area.Type))
colnames(dt5) <- c('Area.Type', 'Count')
dt5

Area.Type	Count
A	14
B	0
C	0
D	11

Thus, Fredericksburg has 14 projects in area type A and 11 in D for a total of 25 projects. In the technical guide, Table 4.2 on p. 36, the factor weights by area type are as follows:

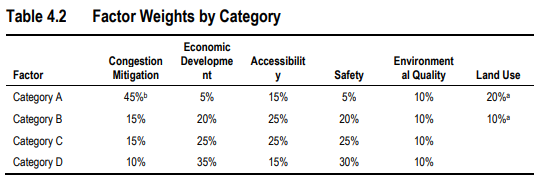
alt text

Since all Fredericksburg projects are within area types A and D, we will reassign priorities as follows. In type A, we will give Accessibility a weight of 45% and Congestion Mitigation a weight of 15%. In type D we will give Accessibility a weight of 35% and Economic Development a weight of 15%.

Below we will recalculate the Smart Scale Scores and percentile ranges under each assumption and see how this changes the distribution of Fredericksburg projects.

5.1 Calculation of Smart Scale Scores Under Scenarios 2 and 3¶

We begin by calculating the new SSS for scenarios 2 and 3 below.

In [15]:

# ------ Recalculate for scenario 2
# Recalculate Project Benefit with revised weightings and add the new column to the data.
data['Calc.Project.Benefit.Score.Scenario.2'] <- calc.proj.value(data, weight.a=c(0.15, 0.05, 0.45, 0.05, 0.1, 0.2),
                                                                       weight.d=c(0.10, 0.15, 0.35, 0.3, 0.1))
# Add a new SSS column under the scenario 2 assumptions
data['Calc.SMART.SCALE.Score.Scenario.2'] <- (1e7 * data[['Calc.Project.Benefit.Score.Scenario.2']] / 
                                              data[['SMART.SCALE.Request']]) 

# ------ Recalculate for scenario 3
# First, adjust the Fredericksburg Access.to.Jobs values by the designated factor.
a2j.factor <- 1.5
for(i in 1:nrow(data)) {
    if(data[i, 'District'] == 'Fredericksburg') {data[i, 'Access.to.Jobs'] = a2j.factor * data[i, 'Access.to.Jobs']}
}    
# Second, renormalize the Access.to.Jobs column.
data$Access.to.Jobs <- 100 * data$Access.to.Jobs / max(data$Access.to.Jobs)
    
# Third, recalculate the Accessibility factor
data$Accessibility.Score <- weighted.column.average(data, c(0.6, 0.2, 0.2), 
                                                    c('Access.to.Jobs', 'Disadvantaged.Access.to.Jobs', 
                                                      'Multimodal.Access.Score'))
    
# Fourth, add a new column to data with our calculated project benefit scores for scenario 3
data['Calc.Project.Benefit.Score.Scenario.3'] <- calc.proj.value(data, weight.a=c(0.15, 0.05, 0.45, 0.05, 0.1, 0.2),
                                                                       weight.d=c(0.10, 0.15, 0.35, 0.3, 0.1))

# Fifth, add a new SSS column under the scenario 3 assumptions
data['Calc.SMART.SCALE.Score.Scenario.3'] <- (1e7 * data[['Calc.Project.Benefit.Score.Scenario.3']] / 
                                              data[['SMART.SCALE.Request']])

5.2 Comparison of Scenarios¶

Below we perform the comparisons of scenarios. We first look at the number of Fredericksburg projects falling into different Smart Scale Score percentile bands in each scenario. By ranking the discrete percentile bands from 1 being the lowest to 8 being the highest, we then compare the average percentile ranking of Smart Scale scores for the Fredericksburg projects under each scenario.

In [16]:

# For a list of ranges and a vector, this function tabulates the counts by range.
tabulate.by.ranges <- function(v, ranges) {
  counts <- c()
  ranges <- sort(ranges)
  i <- 1
  for(i in 1:length(ranges)) {
    if(i == 1) {
      counts[1] <- sum(v <= ranges[1])
    }
    else {
      counts[i] <- sum((v > ranges[i - 1]) & (v <= ranges[i]))
    }
  }
  counts
}

# Compare the scenarios.
sss1.ord <- sort(data$SMART.SCALE.Score)
sss2.ord <- sort(data$Calc.SMART.SCALE.Score.Scenario.2)
sss3.ord <- sort(data$Calc.SMART.SCALE.Score.Scenario.3)
percentiles <- c(0.05, 0.1, 0.25, 0.5, 0.75, 0.9, 0.95, 1) 
cut.scores.1 <- sapply(percentiles, function(p){sss1.ord[ceiling(p * nrow(data))]})
cut.scores.2 <- sapply(percentiles, function(p){sss2.ord[ceiling(p * nrow(data))]})
cut.scores.3 <- sapply(percentiles, function(p){sss3.ord[ceiling(p * nrow(data))]})

fb <- subset(data, District=='Fredericksburg')

counts.1 <- tabulate.by.ranges(fb$SMART.SCALE.Score, cut.scores.1)
counts.2 <- tabulate.by.ranges(fb$Calc.SMART.SCALE.Score.Scenario.2, cut.scores.1)
counts.3 <- tabulate.by.ranges(fb$Calc.SMART.SCALE.Score.Scenario.3, cut.scores.3)

perc.range <-  c('0-5%', '5-10%', '10-25%', '25-50%', 
                 '50-75%', '75-90%', '90-95%', '95-100%')

scenarios <- data.frame(Percentile_Rank=1:length(perc.range),
                        Percentile_Band=perc.range,
                        Scenario_1_Fredericksburg_Project_Count=counts.1,
                        Scenario_2_Fredericksburg_Project_Count=counts.2,
                        Scenario_3_Fredericksburg_Project_Count=counts.3)
scenarios

avg.perc.rank <- data.frame(Scenario=1:3,
                    Average_Fredericksburg_Percentile_Rank=c(sum(scenarios$Percentile_Rank * counts.1) / sum(counts.1),
                                                             sum(scenarios$Percentile_Rank * counts.2) / sum(counts.2),
                                                             sum(scenarios$Percentile_Rank * counts.3) / sum(counts.3)),
                            Average_Fredericksburg_Smart_Scale_Score=c(mean(fb$SMART.SCALE.Score),
                                                                       mean(fb$Calc.SMART.SCALE.Score.Scenario.2),
                                                                       mean(fb$Calc.SMART.SCALE.Score.Scenario.3)))
avg.perc.rank

Percentile_Rank	Percentile_Band	Scenario_1_Fredericksburg_Project_Count	Scenario_2_Fredericksburg_Project_Count	Scenario_3_Fredericksburg_Project_Count
1	0-5%	0	0	0
2	5-10%	2	2	1
3	10-25%	5	5	4
4	25-50%	7	8	9
5	50-75%	5	4	5
6	75-90%	3	3	2
7	90-95%	2	2	3
8	95-100%	1	1	1

Scenario	Average_Fredericksburg_Percentile_Rank	Average_Fredericksburg_Smart_Scale_Score
1	4.48	8.902320
2	4.44	8.645798
3	4.64	8.861798

In the first table above we see the counts of projects within the Fredericksburg district arranged by percentile under scenarios 1 (current), 2 (prioritization of Accessibility factor for area types A and D), and 3 (prioritization of Accessibility factor for area types A and D + 1.5x increased "Access to Jobs" measures for Fredericksburg district). In the second table we see the average Fredericksburg percentile rank and average Fredericksburg Smart Scale Scores for each scenario. Two observations are apparent:

There is no major difference between scenarios 1 and 2.
There is a modest upward movement in Fredericksburg project percentile rank in scenario 3 (which prioritizes the Accessibility factor and also increases the weighting factor by 1.5), with the 25-50% and 90-95% bands seeing increases in the number of Fredericksburg projects. Of the 25 Fredericksburg projects in the dataset, two projects moved up into the 25-50% band and one more moved up into 90-95% band.

5.3 Synopsis and Conclusions¶

The Smart Scale methodology (as specified in the Nov. 2017 technical guide) places a relatively low priority on the Accessibility factor in area types A and D and only considers a 45-minute radius. This does not entirely reflect the unique commuter conditions found in the Fredericksburg region. The value of some projects in this region may accordingly be underestimated and, depending on the cut score, these projects may be edged out of funding.

VI. Conclusions¶

This study performed a statistical analysis on a set of 404 transportation projects scored using the Virginia Smart Scale methodology. Descriptive statistics were first provided which characterize the data over several project features. An analysis was then performed to see whether the Smart Scale methodology was applied consistently to these projects, which entailed replicating the score calculations as specified in the November 2017 Technical Guide and comparing them to the assigned scores. The results indicate that the scoring methodolgy was applied consistently to the projects. Finally, the study considered whether increasing the emphasis on Accessibility in the scoring calculation would increase the competitiveness of projects within the Fredericksburg area. The results indicate that increasing the emphasis on Accessibility and considering a larger radius would lead to small increases in average percentile ranking for some Fredericksburg projects. Accordingly, because Fredericksburg has such a large percentage of its workforce which commutes outside the area, the impact of these projects may be underestimated by using the current Smart Scale methodology.

References¶

[1] Hansen, B.A. (2016). "Fredericksburg Region Commuter Workforce Skills Study", University of Mary Washington study prepared for the Fredericksburg Regional Alliance and the Fredericksburg Regional Chamber of Commerce, Accessed at http://www.umw.edu/news/wp-content/uploads/sites/7/2016/05/Report-on-Commuters-FINAL_mm.pdf

In [ ]: