Die Entdeckung von Teilchen mithilfe von "CERN Open Data"¶
Der sogenannte Large Hadron Collider (LHC) am CERN in Genf wurde weltbekannt durch die Entdeckung des Higgsboson in 2012. Im Rahmen dieser Aufgabe wirst du echte Daten vom LHC verwenden um etwas darüber zu lernen wie dieser Durchbruch gelungen ist und hoffentlich selber ein Teilchen entdecken!

Teilchenkollisionen¶
Mithilfe des LHC vesuchen Forscher die kleinsten Bestandteile von Materie zu finden indem sie Protonenstrahlen, die sich annähernd mit Lichtgeschwindigkeit bewegen, kollidieren lassen. Die Energie, die bei dieser Kollision beteiligt ist, lässt Teilchen verschiedenster Art entstehen. In den Detektoren von CMS und ATLAS (beides Detektoren am LHC am CERN) werden die Teilchen, die bei diesen Kollisionen entstehen, untersucht und verschiedene Größen gemessen. Die Geschwindigkeit mit der die Daten entstehen ist unglaublich: der LHC produziert jede Sekunde 40 000 000 Teilchenkollisionen!
Manche Teilchen, die bei dieser Kollision entstehen (z.B.: Elektronen und Myonen) können direkt von den Dedektoren erfasst werden. Manche exotische und spannende Teilchen (wie z.B. das Higgsboson) haben allerdings eine sehr kurze Lebensdauer und zerfallen in weitere Teilchen bevor sie der Detektor erfassen kann. Woher wissen wir also, dass sie überhaupt da waren?
Die Jagd nach dem J/$\Psi$¶
Wir suchen nach dem Beweis für eines dieser kurzlebigen Teilchen namens J/$\psi$. Die Existenz dieses Teilchens, das aus einem Charm- und eine Anticharmquark besteht, wird durch das Standardmodell der Teilchenphysik vorausgesagt. Die Lebensdauer beträgt $7,2 \cdot 10^{-21}$ s, danach zerfällt es in weitere Teilchen. Die Lebensdauer des Teilchens ist viel zu kurz um es mit Detektoren vom LHC zu beobachten. Glücklicherweise wissen wir, dass das J/$\psi$-Teilchen in ein Myon-Antimyon-Paar zerfällt. Dieses Paar kann mithilfe von Dedektoren erfasst werden. Da neben dem J/$\psi$-Teilchen auch andere Teilchen entstehen, die ebenfalls in Myonen oder Antimyonen zerfallen können, erfasst der Detektor nicht nur die Myonen vom J/$\psi$, sondern auch tausende weitere. Dieses Problem muss zuerst behoben werden bevor wir weiter über die Entdeckung des J/$\psi$-Teilchen sprechen können.
Invariante Masse¶
Es gibt einen Trick den Teilchenphysiker verwenden, wenn sie Daten von Detektoren analysieren. Durch die Kombination von Energie und Impuls einer Teilchenpaars (in unserem Fall eines Myons und eines Antimyons) auf eine bestimmte Weise kann die sogenannte "Invariante Masse" des ursprünglichen Teilchens bestimmt werden. Wenn die zwei Teilchen tatsächlich durch den Zerfall des ursprünglichen Teilchens enstanden sind, dann wird mit dieser Größe die Masse des ursprünglichen Teilchens erfasst (Einheit: $GeV/c^2$). Wenn durch unsere Kollision viele J/$\psi$-Teilchen entstehen, dann müssten wir auch viele Paare von Myonen finden, die zurückgerechnet genau die vorausgesagte invariante Masse des J/$\psi$ ergeben.
Um diesen Vorgang zu verstehen und die Existenz eines Teilchens zu bestätigen müssen wir einige Daten analysieren.
Jupyter Notebooks¶
Das Dokument, das du vor dir siehst, ist ein Jupyter Notebook. Es wird von professionellen Wissenschaftlern am CERN (und auch in anderen Institutionen) verwendet um Daten vom LHC zu analysieren. Jupyter Notebooks bestehen aus Textzellen wie dieser und Codezellen, wie du sie unterhalb siehst. In den Codezellen kann die Programmiersprache "Python" verwendet werden. Um die Zelle auszuführen musst du Strg + Enter drücken. Probier es unterhalb gleich mal aus! (Der dargestellte Code wird verwendet um verschiedene Softwarepakete zu laden, die wir später benötigen.)
#lines of code writen with a hashtag like this are comments, and will be ignored when you run the code.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Der Umgang mit "Open Data"¶
1. Daten lesen¶
Es gibt unzählige open-data-Portale die Daten verschiedenster Art zur Verfügung stellen.
In unserem Fall verwenden wir das open-data-Portal, das von CERN zur Verfügung gestellt wird: (http://opendata.cern.ch/)
Um die Daten lesen zu können müssen wir folgende Funktion verwenden: pd.read_csv.
Der Link zum Datenportal ist das Argument der Funktion pd.read_csv(Argument).
Hinweis: Die Daten sollten im .csv-Format verfügbar sein.
Beispiel:
muons = pd.read_csv(' URL ')
Hinweis: Wenn du in diesem Notebook einen Beispielcode vorfindest solltes du die grünen Teile beibehalten und die roten Teile verändern.
Aufgabe 1.
Beginnen wir mit der Suche nach dem J/ψ indem wir reale Daten vom CMS-Experiment am CERN laden. CERN stellt Daten öffentlich zur Verfügung um genau solche Projekte wie dieses hier zu unterstützen!
Erstelle eine Datenreihe namens "muons", welche die Daten von folgender Website einliest. Verwende dazu den Beispielcode von oben und folgende URL: http://opendata.cern.ch/record/545/files/Dimuon_DoubleMu.csv
2. Daten sichtbar machen.¶
Wie dir wahrscheinlich aufgefallen ist, scheint es, als ob nichts passiert wäre. Die Information und die Daten sind in der Zelle gespeichert, bleiben für dich allerdings unsichtbar.
Um herauszufinden wieviel Daten wir geladen haben müssen wir sie allerdings genauer betrachten können. Da die Daten in Form einer Tabelle gepeichert sind müssen wir nur die Anzahl an Zeilen zählen (diese Zahl enspricht der Anzahl an Messungen im Experiment).
Voraufgabe:
F: Rate wie Länge die Datentabelle sein wird, die du gerade geladen hast und tippe deine Schätzung in die nächste Zeile:
A:
Um die Länge der Datentabelle zu ermitteln wird die "len"-Funktion verwendet:
Beispiel:
len(Name_der_Daten)
Aufgabe 2. Bestimme die Länge der Datenreihe, indem du den Code in die Zelle unterhalb tippst.
Aufgabe 3. Dikussion: Warum benötigen wir so viele Daten?
Aufgabe 4. Brainstorming: Welche Größen könnten bei diesem Experiment interessant sein zu messen. Tippe einige Vermutungen in die Textzelle unterhalb.
A:
Aufgabe 5.
Nun wird es Zeit einen genaueren Blick auf den Inhalt unserer Daten zu werfen. Um uns die ersten 5 Zeilen der Daten anzusehen müssen wir die "head"-Funktion verwenden.
Beispiel:
Name_der_Daten.head()
Verwende die Codezelle unterhalb um die ersten 5 Zeilen unserer Daten zu enthüllen.
3. Daten verstehen¶
Wie du siehst sind in der Tabelle die Größen zweier Teilchen aufgelistet (wie wir wissen muss es ein Myon-Antimyonpaar sein). Die Größen wurden nach der Kollision vom Detektor erfasst und berechnet. Jede Spalte, die mit dem Index 1 oder 2 beschriftet ist steht für eine Größe, die zu Teilchen 1 oder 2 gehört.
E - Energie des Teilchen
px, py, pz - x,y,z-Komponenten der Impulse der Teilchen
pt - Die Kombination von px und py (Der Teil des Impulses der normal auf den Impuls des Teilchenstrahls steht)
eta, phi - Winkel die die Richtung der Bewegung der Teilchen angeben
Q - Elektrische Ladung der Teilchen in Elementarladungen
M - Invariante Masse des Myonenpaars
Hinweis: Physiker im Bereich Teilchenphysik verwenden sogenannte "Natürliche Einheiten" für diese Größen. Diese Einheiten verwenden die berühmte Formel von Einstein E=mc$^2$ um Energie, Impuls und Masse in folgenden Einheiten anzugeben: GeV, GeV/c und GeV/c$^2$.

4. Präsentation der Daten¶
Wir haben nun viele Daten in Form einer Tabelle zur Verfügung. Dies ist sicher nicht die beste Art der Darstellung Daten um sie analysieren zu können und um schlussendlich das J/$\psi$-Teilchen zu finden.
Für eine bessere Darstellung der Daten können Histogramme verwendet werden.
Kurzer Exkurs in die Erstellung eines Histogramms:
Schritt 1.
"Bin" (die Klassen der Daten) - unerteilt die gesamte Bandbreite der Daten (zum Beispiel die Teilchenenergie) in eine kleiere Anzahl an Intervallen. Die "bins" oder Klassen sind nacheinander folgende sich nicht überlappende Intervalle der Variablen.
Die "bins" sind angrenzend und üblicherweise gleicher Breite.
Schritt 2.
Anzahl der Werte in einem Intervall bestimmen: Wenn die "bins" gleiche Größe haben dann ist die Höhe des Rechtecks dividiert durch die Breite der Klasse proportional zur Anzahl der Daten in der Klasse.
Beispiel Histogramm
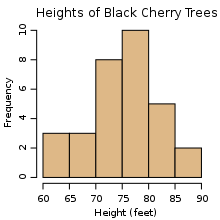
Wir verwenden nun einen Code um ein Histogramm zu erstellen:
Beispiel:
fig = plt.figure( figsize=(15, 10)) (Diese Zeile bestimmt die Größe des Histogramms und beinhaltet einen x-Wert und einen y-Werte (wie die Länge und Breite eines Rechtecks)
plt.hist(Name_der_Daten.Name_der_Spalte, Anzahl_bins , range = (min , max)) (Diese Zeile plotted das Histogramm anhand der Parameter in den Klammern; "range" bestimmt die Grenzen für die Werte der x-Achse)
plt.xlabel('Bezeichnung_x-Achse, Einheit \n', fontsize = 15) (Diese Zeile beschriftet die x-Achse. Die Zahl "fontsize" wird verwendet um die Größe des Texts zu bestimmen. Das Symbol /n erstellt eine neue Zeile und lässt den Plot schöner aussehen)
plt.ylabel('Number of Events \n', fontsize = 15) (Diese Zeile beschriftet die y-Achse)
plt.title('Titel \n', fontsize = 15) (In dieser Zeile wird der Titel für den Plot festgelegt.)
plt.show()
Aufgabe 6 Zeichne ein Histogramm für die Invariante Masse (M) deiner Daten in der Codezeile unterhalb.
Vorschlag : Um das infromativste Bild zu erhalten, solltest du eine Bandbreite für die Invariante Masse zwischen 0-150 verwenden und verschiedene Zahlen für die "bins" ausprobieren (starte bei 200). Es gibt keine "richtige" Anzahl an "bins", allerdings können durch verschiedene "bin"-Zahlen verschiedene Informationen sichtbar werden. Wähle weise.
Aufgabe 7. Was kannst du erkennen? Schreibe in der Textzelle unterhalb einige allgemeine Beobachtungen nieder und beziehe dich dabei auf das Histogramm.
A:
5. Schauen wir uns die Daten genauer an.¶
Glückwunsch! Du hast soben die kompletten Daten geplottet und somit eine schöne Übersicht über die Invariante Masse der 100 000 erfassten Myonenpaare gewonnen.
Gehen wir nun einen Schritt weiter:
Unser Hauptziel war ein neues Teilchen zu finden!
Theoretische Voraussagen von 1974 sagen eine Wahrscheinlichkeit von 6% für den Zerfall eines J/$\psi$-Teilchen in ein Myonenpaar voraus. Das J/$\psi$-Teilchen soll dabei eine Masse von rund $3 GeV/c^2$ und eine Lebensdauer von $7,2\cdot10^{-21} s$ haben.
Aufgabe 8. Beantworte die Fragen unterhalb:
F: Welche Information von der Textzelle oberhalb ist für uns relevant um einen genaueren und sinnvollen Blick auf die Daten werfen zu können?
A:
F: Was bedeutet es eine Masse von $3 GeV/c^2$ zu haben? In welchem Zusammenhang steht die Einheit GeV zur SI-Einheit "kg"?
A:
Wenn wir in den Plot hineinzoomen und einen kleinen Teil des Histogramms genauer untersuchen wollen, müssen wir unsere Daten auf den Teil beschränken, der uns interessiert. Danach müssen wir das neue Datenset plotten. Hier ist ein Beispiel für die bestimmung des limitierten Datensets:
Beispiel:
Name_des_beschränkten_Datensets = Name_der_originalen_Daten[(Name_der_originalen_Daten.Name_der Spalte >= untere_Grenze) & (Name_der_originalen_Daten.Name_der_Spalte <= obere_Grenze)]
Aufgabe 9. Verwende die Codezeile unterhalb um ein neues Datenset zu erstellen, das an unsere Bedürfnisse derart angepasst ist um das J/$\psi$-Teilchen zu finden.

Aufgabe 10. Verwende die Codezeile unterhalb um ein Histogramm zu plotten, das das neue Datenset verwendet. Siehe wenn nötig unter Abschnitt 4 nach wie ein Histogramm geplotted wird. Vielleicht musst du für das neue Datenset ein paar Paramter verändern.
6. Reflexionsfragen¶
F: Was zum Henker mach ich hier?
A:
F: Wie kann das Histogramm von oben verwendet werden um den Beweis für die Existenz des J/$\psi$-Teilchen zu liefern?
A:
F: Welche physikalischen Messungen mussten vorgenommen werden um diesen Beweis hervorzubringen?
A:
F: Glaubst du, dass das Histogramm die theoretischen Vorhersagen stützt?
A:
F: Warum können wir nicht eine "eindeutige" Masse unseres Teilchens erkennen und sehen stattdessen eine Bandbreite an Massen?
A:
F: Zähle die grundlegenden Schritte auf, die du auf deinem Weg zum finalen Plot gehen musstest und beschreibe die einzelnen Schritte kurz.
A:
F: Was denkst du: Können diese Schritte auch zur Lösung andere wissenschaftliche Probleme verwendet werden? Wieso?
A:
F: Wie kann das open-data-Portal von CERN verwendet werden um andere Teilchen zu finden?
A:
F: Warum verwenden Wissenschafler Programmiersprache wie Python und Software wie Jupyter um großen Datenmengen zu analysieren?
A:
Hier findest du weiterführende Informationen über das Teilchen, dass du soeben entdeckt hast:
https://www.symmetrymagazine.org/breaking/2008/05/16/the-jpsi-particle-original-papers



