
This is a preview chapter from my upcoming book, Mathematics of Machine Learning. The book is currently work in progress, but the early access version will be released soon. If you are interested in more, sign up for updates or follow me on Twitter!
PCA¶
The ability to look at the data with your eyes is one of the most under-appreciated things in machine learning. Before any machine learning is done, visualizing the data can reveal a lot of patterns. Exploring them can pay huge dividends later, as we can get a good intuition about what algorithm to use, which features to omit, etc.
However, there is a big issue: humans cannot see in dimensions larger than three. So, for real-life datasets, we have to perform certain tricks to benefit from the insight that visualization can provide.
The Principal Component Analysis (PCA) is one of the most basic and useful methods for this purpose. PCA linearly transforms the data into a space that highlights the importance of each new feature, thus allowing us to prune the ones that don't reveal much.
First, we will get an intuitive understanding of PCA, and then we proceed with a more detailed mathematical treatment.
The idea behind PCA¶
To get a good grip on what PCA does, we shall see how it performs on a simple dataset, visualized below.

Let $ X \in \mathbb{R}^{d \times n} $ denote our dataset. Each column encodes a sample, and each row represents a feature. For simplicity, we shall assume that $ d = 2 $ so we can visualize what is happening. However, all that will be said holds for the general case.
What we can observe right away is that the features $ x_1 $ and $ x_2 $ are perhaps not the best descriptors of our data. The distribution seems to be stretched out across both variables, although the shape suggests that the data can be simplified from a particular viewpoint. The features seem correlated: if $ x_1 $ is small, then $ x_2 $ is large. If $ x_1 $ is large, $ x_2 $ is small. This means that the variables contain redundant information. Redundancy is suboptimal when we have hundreds of features. If we could reshape the data to a form where the variables are uncorrelated and ordered according to importance, we would be able to discard those that are not that expressive.
We can formulate this process in the language of linear algebra. To decorrelate the data, we are looking to diagonalize the covariance matrix of $ X $. Since the covariance matrix is symmetric, the spectral decomposition theorem guarantees as an orthogonal matrix $ U $ such that
$$ U^T \widehat{\mathrm{Cov}}[X] U = \Lambda = \mathrm{diag}(\lambda_1, \dots, \lambda_n). $$(Recall that a matrix $ U $ is orthogonal if $ U^{-1} = U^T $.) From the spectral theorem, we also know that we can select $ \Lambda $ such that the diagonal elements are in decreasing order. Due to the behavior of empirical covariance under linear transformations, we can see that
$$ \begin{align*} U^T \widehat{\mathrm{Cov}}[X] U &= U^T \widehat{\mathrm{Cov}}[X - \overline{X}] U \\ &= \widehat{\mathrm{Cov}}[U^T(X - \overline{X})]. \end{align*} $$If we define $ Y $ by
$$ Y := U^T(X - \overline{X}), $$we can notice a few things right away. First, that $ X = UY + \overline{X} $, so $ X $ and $ Y $ are linear transformations of each other. Second, that $ \hat{\mathbb{E}}[Y] = 0 $, so the data is perfectly centered. However, most importantly, $ \widehat{\mathrm{Cov}}[Y] = \Lambda $ is diagonal. In other words, the features of $ Y $ are uncorrelated, which was our goal.
This is the essence of principal component analysis. Recall from the spectral decomposition theorem that the rows of $ U $ (denoted by $ u_i $) form an orthonormal basis. In our new feature space, the data is described in terms of the $ u_i $ vectors. $ Y $ is called the principal component vector of $ X $, while its features are called principal components.
Applied to our simple dataset, this is the result.

Note that since the components of $ \widehat{\mathrm{Cov}}[Y] $ are variances, they are all positive.
Each feature of $ Y $ is a linear combination of the features of $ X $. As we shall see next, this is not their only special property.
The principal components maximize variance¶
Besides the uncorrelated nature $ Y $, one thing makes its features unique: each principal component is maximizing the variance of the data when projected on it.

We can make this a bit more precise. Let's project the entire dataset onto a single feature vector! For each unit vector $ v $, the transformation
$$ v^T (X - \overline{X}) \in \mathbb{R}^{1 \times n} $$defines this projection. (If you are wondering why, here is an explanation.) In case of $ v = u_i $, the result is the $ i $-th principal component vector! It turns out that $ u_1 $ is the unit vector that maximizes the variance of this transformation. Indeed, we have
$$ \begin{align*} \widehat{\mathrm{Cov}}\Big[v^T (X - \overline{X})\Big] &= v^T \widehat{\mathrm{Cov}}\Big[ (X - \overline{X})\Big] v. \end{align*} $$We encountered this quantity when we talked about the spectral decomposition! Since $ u_1 $ is the first column of the diagonalizing orthogonal matrix,
$$ u_1 = \mathrm{arg} \max_{\| v \| = 1} v^T \widehat{\mathrm{Cov}}\Big[ (X - \overline{X})\Big] v $$holds. In fact, even more is true: in general, the $ k $-th principal component $ u_k $ is the unit vector that is orthogonal to $ u_1, \dots, u_{k-1} $ and maximizes the covariance of the projected data. Putting it into formulas,
$$ u_k = \mathrm{arg} \max_{\| v \| = 1 \\ v \perp u_1, \dots, u_{k-1}} v^T \widehat{\mathrm{Cov}}\Big[ (X - \overline{X})\Big] v $$holds.
In plain English, the $ k $-th principal component is selected such that
- it is uncorrelated with the previous ones, so it doesn't contain any redundant information,
- and it maximizes the available information (by maximizing variance).
Dimensionality reduction with PCA¶
Now that we understand how PCA works, we should look into what it does with real datasets. Besides eliminating redundancies in the features, it can also be used to prune those that don’t convey much information. Recall that the covariance matrix of $ Y = U^T(X - \overline{X}) $ is diagonal, and the features' variance are ordered in decreasing order:
$$ \widehat{\mathrm{Cov}}[Y] = \begin{bmatrix} \widehat{\mathrm{Cov}}[y_1] & 0 & \dots & 0 \\ 0 & \widehat{\mathrm{Cov}}[y_2] & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & \widehat{\mathrm{Cov}}[y_n] \end{bmatrix}, \quad \widehat{\mathrm{Cov}}[y_1] \geq \widehat{\mathrm{Cov}}[y_2] \geq \dots \widehat{\mathrm{Cov}}[\mathbf{y}_n]. $$The explained variance of $ y_k $ is defined by the ratio
$$ \frac{\widehat{\mathrm{Cov}}[y_k]}{\sum_{i=1}^{n} \widehat{\mathrm{Cov}}[y_i] } \in [0, 1], $$which can be thought of as the percentage of "all the variance" in the data. Since the variances are decreasing, the most meaningful features come first. This means that if the cumulative explained variance
$$ \sum_{j=1}^{k} \frac{\widehat{\mathrm{Cov}}[y_j]}{\sum_{i=1}^{n} \widehat{\mathrm{Cov}}[y_i] } $$is large enough for some $ k $, say around $ 90\% $, principal components after $ k $ can be dropped without significant information loss.
To see how it performs on real data, we will see how PCA performs on the famous Iris dataset! This dataset consists of four features (sepal length, sepal width, petal length, petal width) from three different kinds of irises: Setosa, Versicolour, and Virginica. This is how the dataset looks.

Upon inspection, we can see that some combination of features separates the data well, some don’t. Their order definitely doesn’t signify their importance. By calculating the covariance matrix, we can also notice that they seem to be correlated:
[[ 0.68112222 -0.04215111 1.26582 0.51282889]
[-0.04215111 0.18871289 -0.32745867 -0.12082844]
[ 1.26582 -0.32745867 3.09550267 1.286972 ]
[ 0.51282889 -0.12082844 1.286972 0.57713289]]
Let's apply PCA to see what it does with our dataset!
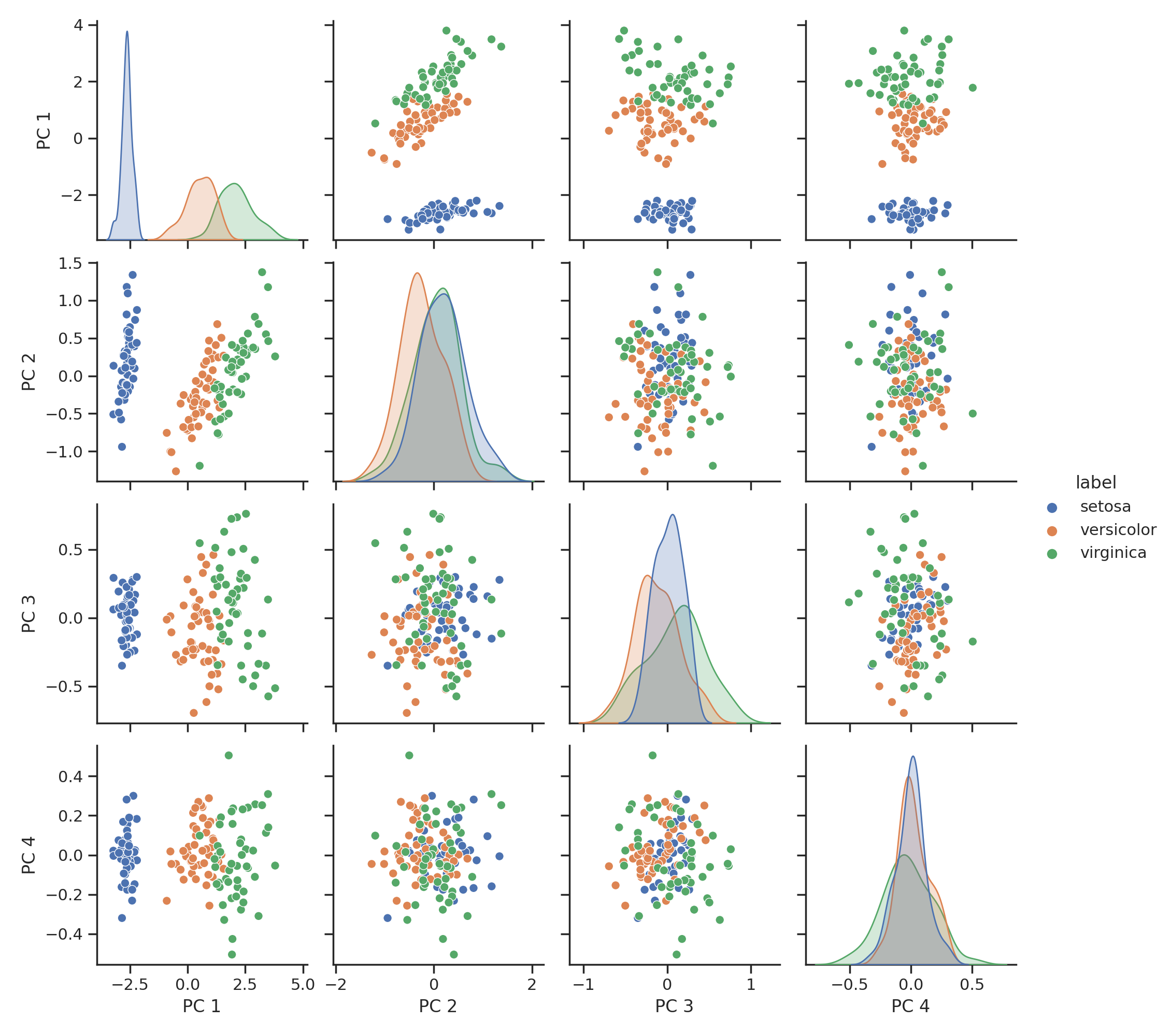
The first two principal component almost completely describe the dataset, while the 3rd and 4th can be omitted without noticeable loss of information. The covariance matrix also looks much better. It is essentially diagonal, so the features are not correlated with each other.
[[ 1.57502004e+02 -3.33667355e-15 2.52281147e-15 5.42949940e-16]
[-3.33667355e-15 9.03948536e+00 1.46458764e-15 1.37986097e-16]
[ 2.52281147e-15 1.46458764e-15 2.91330388e+00 1.97218052e-17]
[ 5.42949940e-16 1.37986097e-16 1.97218052e-17 8.87857213e-01]]
What the PCA doesn't do¶
Although PCA is frequently used for feature engineering, there are limits on what it can do. For instance, if the dataset is thinly stretched out and the separating margin is small between them (like the example below), PCA won’t provide a representation where the difference between classes is sharper.

The reason is that the principal component vectors are given by an orthogonal transformation, and orthogonal transformations preserve distance. So, this doesn't stretch the space along any features. This is an advantage and a disadvantage at the same time. (In two dimensions, an orthogonal transformation is just a composition of rotations and reflections.)
Appendix: references¶
A few references in this preview chapter are required for complete understanding but are located elsewhere in the book. For the sake of completeness, I have included them here.
The spectral decomposition theorem¶
Theorem. Let $ A \in \mathbb{R}^{n \times n} $ be a real symmetric matrix. (That is, $ A^T = A $.) Then $ A $ has exactly $ n $ real eigenvalues $ \lambda_1 \geq \dots \geq \lambda_n $, and the corresponding eigenvectors $ u_1, \dots, u_n $ can be selected such that they form an orthonormal basis.
Moreover, if we let $ \Lambda = \mathrm{diag}(\lambda_1, \dots, \lambda_n) $ and $ U $ be the orthogonal matrix whose rows are $ u_1, \dots, u_n $, then
$$ A = U \Lambda U^T $$holds.
The variance-maximizing property of the eigenvalue basis¶
The orthogonal matrix $ U $ and the corresponding orthonormal basis $ \{ u_1, \dots, u_n \} $ that diagonalizes a symmetric matrix $ A $ has a special property that is very important when discussing principal component analysis.
Theorem. Let $ A \in \mathbb{R}^{n \times n} $ be a real symmetric matrix and let $ \lambda_1 \geq \dots \geq \lambda_n $ be its real eigenvalues in decreasing order. Moreover, let $ U \in \mathbb{R}^{n \times n} $ be the ortogonal matrix that diagonalizes $ A $, with the corresponding orthonormal basis $ \{ u_1, \dots, u_n \} $.
Then
$$ \mathrm{arg}\max_{\| x \| = 1} x^T A x = u_1, $$and
$$ \max_{\| x \| = 1} x^T A x = \lambda_1. $$Proof. Since $ \{ u_1, \dots, u_n \} $ is an orthonormal basis, any $ x $ can be expressed as a linear combination of them:
$$ x = \sum_{i=1}^{n} x_i u_i, \quad x_i \in \mathbb{R}. $$Thus, since $ u_i $ are the eigenvectors of $ A $,
$$ \begin{align*} Ax &= A \Big( \sum_{i=1}^{n} x_i u_i \Big) = \sum_{i=1}^{n} x_i A u_i = \sum_{i=1}^{n} x_i \lambda_i u_i. \end{align*} $$Plugging it back into $ x^T A x $, we have
$$ \begin{align*} x^T A x &= \Big( \sum_{j=1}^{n} x_j u_j \Big)^T A \Big( \sum_{i=1}^{n} x_i u_i \Big) \\ &= \Big( \sum_{j=1}^{n} x_j u_j^T \Big) A \Big( \sum_{i=1}^{n} x_i u_i \Big) \\ &= \Big( \sum_{j=1}^{n} x_j u_j^T \Big) \Big( \sum_{i=1}^{n} x_i \lambda_i u_i \Big) \\ &= \sum_{i,j=1}^{n} x_i x_j \lambda_i u_j^T u_i. \end{align*} $$Since the $ u_i $-s form an orthonormal base,
$$ u_j^T u_j = \begin{cases} 1 \quad \text{if } i = j, \\ 0 \quad \text{otherwise.} \end{cases} $$In other words, $ u_i^T u_j $ vanishes when $ i \neq j $. Continuing the above calculation with this observation,
$$ \begin{align*} x^T A x &= \sum_{i,j=1}^{n} x_i x_j \lambda_i u_j^T u_i = \sum_{i=1}^{n} x_i^2 \lambda_i. \end{align*} $$When $ \| x \|^2 = \sum_{i=1}^{n} x_i^2 = 1 $, the sum $ \sum_{i=1}^{n} x_i^2 \lambda_i $ is a weighted average of the eigenvalues $ \lambda_i $. So,
$$ \sum_{i=1}^{n} x_i^2 \lambda_i \leq \sum_{i=1}^{n} x_i^2 \max_{k = 1, \dots, n} \lambda_k = \max_{k = 1, \dots, n} \lambda_k = \lambda_1, $$from which $ x^T A x \leq \lambda_1 $ follows. (Recall that we can assume without loss in generality that the eigenvalues are decreasing.) On the other hand, by plugging in $ x = u_1 $, we can see that $ u_1^T A u_1 = \lambda_1 $, so the maximum is indeed attained. From these two, the theorem follows. $ \square $
The mathematical formalization of the above result doesn't reveal much. At this point, we don't have all the tools to see, but in connection to the principal component analysis, this says that the first principal vector is the one that maximizes variance.
Moreover, this was just a special case. The general theorem is as follows.
Theorem. Let $ A \in \mathbb{R}^{n \times n} $ be a real symmetric matrix, let $ \lambda_1 \geq \dots \geq \lambda_n $ be its real eigenvalues in decreasing order. Moreover, let $ U \in \mathbb{R}^{n \times n} $ be the ortogonal matrix that diagonalizes $ A $, with the corresponding orthonormal basis $ \{ u_1, \dots, u_n \} $.
Then for all $ k = 1, \dots, n $, we have
$$ \mathrm{arg}\max_{\| x \| = 1 \\ x \perp \{ u_1, \dots, u_{k-1} \} } x^T A x = u_k, $$and
$$ \max_{\| x \| = 1 \\ x \perp \{ u_1, \dots, u_{k-1} \}} x^T A x = \lambda_k. $$Proof. The proof is almost identical to the previous one. Since $ x $ is required to be orthogonal to $ u_1, \dots, u_{k-1} $, it can be expressed as
$$ x = \sum_{i=k}^{n} x_i u_i, \quad x_i \in \mathbb{R}. $$Following the calculations in the proof of the previous theorem, we have
$$ x^T A x = \sum_{i=k}^{n} x_i^2 \lambda_i \leq \lambda_k. $$On the other hand, similarly as before, $ u_k^T A u_k = \lambda_k $, so the theorem follows. $ \square $
Empirical covariance¶
The empirical mean of a data sample $ X $ is defined by
$$ \hat{\mathbb{E}}[X] := \frac{1}{m} \sum_{k=1}^{m} x_k, $$while the empirical covariance matrix is given by
$$ \widehat{\mathrm{Cov}}[X] := \frac{1}{m} \big(X - \overline{X}\big) \big(X - \overline{X}\big)^T. $$Like their counterparts, the empirical mean and covariance behave properly with respect to linear transformations. For any $ A, B \in \mathbb{R}^{n \times n} $, we have
$$ \hat{\mathbb{E}}[AX] = A\hat{\mathbb{E}}[X], $$and
$$ \begin{align*} \widehat{\mathrm{Cov}}[AX] &= A \widehat{\mathrm{Cov}}[X] A^T, \\ \widehat{\mathrm{Cov}}[X + m] &= \widehat{\mathrm{Cov}}[X]. \end{align*} $$Inner product as projection¶
When multiplying the vector $ v \in \mathbb{R}^{1 \times d} $ and a matrix $ X \in \mathbb{R}^{d \times n} $ together, $ vX \in \mathbb{R}^{1 \times n} $ contains the inner products of $ v $ with every column of the matrix $ X $.
Based purely on the general definition, it is hard to get an insight into what an inner product does. However, by using the concept of orthogonality, we can visualize what does $ \langle x, y \rangle $ represent for any $ x $ and $ y $.
Intuitively, $ x $ can be decomposed into the sum of two vectors $ x_o + x_p $, where $ x_o $ is orthogonal to $ y $ and $ x_p $ is parallel to it.

How can we find $ x_p $ and $ x_o $? Since $ x_p $ has the same direction as $ y $, it can be written in the form $ x_p = c y $ for some $ c $. Because the two vectors sum up to $ x $, we also have $ x_o = x - x_p = x - c y $. Since this is orthogonal to $ y $, the constant $ c $ can be determined by solving the equation
$$ \langle x - cy, y \rangle = 0, $$from which we obtain
$$ c = \frac{\langle x, y \rangle}{\langle y, y \rangle}. $$So,
$$ \begin{align*} x_p &= \frac{\langle x, y \rangle}{\langle y, y \rangle} y, \\ x_o &= x - \frac{\langle x, y \rangle}{\langle y, y \rangle} y. \end{align*} $$Specifically, if $ y $ is an unit vector, that is, $ \langle y, y \rangle = \| y \| = 1 $ holds, the quantity $ \langle x, y \rangle $ describes the (signed) magnitude of the orthogonal projection of $ x $ onto $ y $.