Chapter 10 – Introduction to Artificial Neural Networks with Keras
This notebook contains all the sample code and solutions to the exercises in chapter 10.
Setup¶
This project requires Python 3.7 or above:
import sys
assert sys.version_info >= (3, 7)
It also requires Scikit-Learn ≥ 1.0.1:
from packaging import version
import sklearn
assert version.parse(sklearn.__version__) >= version.parse("1.0.1")
And TensorFlow ≥ 2.8:
import tensorflow as tf
assert version.parse(tf.__version__) >= version.parse("2.8.0")
As we did in previous chapters, let's define the default font sizes to make the figures prettier:
import matplotlib.pyplot as plt
plt.rc('font', size=14)
plt.rc('axes', labelsize=14, titlesize=14)
plt.rc('legend', fontsize=14)
plt.rc('xtick', labelsize=10)
plt.rc('ytick', labelsize=10)
And let's create the images/ann folder (if it doesn't already exist), and define the save_fig() function which is used through this notebook to save the figures in high-res for the book:
from pathlib import Path
IMAGES_PATH = Path() / "images" / "ann"
IMAGES_PATH.mkdir(parents=True, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = IMAGES_PATH / f"{fig_id}.{fig_extension}"
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris(as_frame=True)
X = iris.data[["petal length (cm)", "petal width (cm)"]].values
y = (iris.target == 0) # Iris setosa
per_clf = Perceptron(random_state=42)
per_clf.fit(X, y)
X_new = [[2, 0.5], [3, 1]]
y_pred = per_clf.predict(X_new) # predicts True and False for these 2 flowers
y_pred
array([ True, False])
The Perceptron is equivalent to a SGDClassifier with loss="perceptron", no regularization, and a constant learning rate equal to 1:
# extra code – shows how to build and train a Perceptron
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(loss="perceptron", penalty=None,
learning_rate="constant", eta0=1, random_state=42)
sgd_clf.fit(X, y)
assert (sgd_clf.coef_ == per_clf.coef_).all()
assert (sgd_clf.intercept_ == per_clf.intercept_).all()
When the Perceptron finds a decision boundary that properly separates the classes, it stops learning. This means that the decision boundary is often quite close to one class:
# extra code – plots the decision boundary of a Perceptron on the iris dataset
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
a = -per_clf.coef_[0, 0] / per_clf.coef_[0, 1]
b = -per_clf.intercept_ / per_clf.coef_[0, 1]
axes = [0, 5, 0, 2]
x0, x1 = np.meshgrid(
np.linspace(axes[0], axes[1], 500).reshape(-1, 1),
np.linspace(axes[2], axes[3], 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = per_clf.predict(X_new)
zz = y_predict.reshape(x0.shape)
custom_cmap = ListedColormap(['#9898ff', '#fafab0'])
plt.figure(figsize=(7, 3))
plt.plot(X[y == 0, 0], X[y == 0, 1], "bs", label="Not Iris setosa")
plt.plot(X[y == 1, 0], X[y == 1, 1], "yo", label="Iris setosa")
plt.plot([axes[0], axes[1]], [a * axes[0] + b, a * axes[1] + b], "k-",
linewidth=3)
plt.contourf(x0, x1, zz, cmap=custom_cmap)
plt.xlabel("Petal length")
plt.ylabel("Petal width")
plt.legend(loc="lower right")
plt.axis(axes)
plt.show()
Activation functions
# extra code – this cell generates and saves Figure 10–8
from scipy.special import expit as sigmoid
def relu(z):
return np.maximum(0, z)
def derivative(f, z, eps=0.000001):
return (f(z + eps) - f(z - eps))/(2 * eps)
max_z = 4.5
z = np.linspace(-max_z, max_z, 200)
plt.figure(figsize=(11, 3.1))
plt.subplot(121)
plt.plot([-max_z, 0], [0, 0], "r-", linewidth=2, label="Heaviside")
plt.plot(z, relu(z), "m-.", linewidth=2, label="ReLU")
plt.plot([0, 0], [0, 1], "r-", linewidth=0.5)
plt.plot([0, max_z], [1, 1], "r-", linewidth=2)
plt.plot(z, sigmoid(z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, np.tanh(z), "b-", linewidth=1, label="Tanh")
plt.grid(True)
plt.title("Activation functions")
plt.axis([-max_z, max_z, -1.65, 2.4])
plt.gca().set_yticks([-1, 0, 1, 2])
plt.legend(loc="lower right", fontsize=13)
plt.subplot(122)
plt.plot(z, derivative(np.sign, z), "r-", linewidth=2, label="Heaviside")
plt.plot(0, 0, "ro", markersize=5)
plt.plot(0, 0, "rx", markersize=10)
plt.plot(z, derivative(sigmoid, z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, derivative(np.tanh, z), "b-", linewidth=1, label="Tanh")
plt.plot([-max_z, 0], [0, 0], "m-.", linewidth=2)
plt.plot([0, max_z], [1, 1], "m-.", linewidth=2)
plt.plot([0, 0], [0, 1], "m-.", linewidth=1.2)
plt.plot(0, 1, "mo", markersize=5)
plt.plot(0, 1, "mx", markersize=10)
plt.grid(True)
plt.title("Derivatives")
plt.axis([-max_z, max_z, -0.2, 1.2])
save_fig("activation_functions_plot")
plt.show()
Regression MLPs¶
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(
housing.data, housing.target, random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train_full, y_train_full, random_state=42)
mlp_reg = MLPRegressor(hidden_layer_sizes=[50, 50, 50], random_state=42)
pipeline = make_pipeline(StandardScaler(), mlp_reg)
pipeline.fit(X_train, y_train)
y_pred = pipeline.predict(X_valid)
rmse = mean_squared_error(y_valid, y_pred, squared=False)
rmse
0.5053326657968465
Classification MLPs¶
# extra code – this was left as an exercise for the reader
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
iris = load_iris()
X_train_full, X_test, y_train_full, y_test = train_test_split(
iris.data, iris.target, test_size=0.1, random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train_full, y_train_full, test_size=0.1, random_state=42)
mlp_clf = MLPClassifier(hidden_layer_sizes=[5], max_iter=10_000,
random_state=42)
pipeline = make_pipeline(StandardScaler(), mlp_clf)
pipeline.fit(X_train, y_train)
accuracy = pipeline.score(X_valid, y_valid)
accuracy
1.0
Let's start by loading the fashion MNIST dataset. Keras has a number of functions to load popular datasets in tf.keras.datasets. The dataset is already split for you between a training set (60,000 images) and a test set (10,000 images), but it can be useful to split the training set further to have a validation set. We'll use 55,000 images for training, and 5,000 for validation.
import tensorflow as tf
fashion_mnist = tf.keras.datasets.fashion_mnist.load_data()
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist
X_train, y_train = X_train_full[:-5000], y_train_full[:-5000]
X_valid, y_valid = X_train_full[-5000:], y_train_full[-5000:]
The training set contains 60,000 grayscale images, each 28x28 pixels:
X_train.shape
(55000, 28, 28)
Each pixel intensity is represented as a byte (0 to 255):
X_train.dtype
dtype('uint8')
Let's scale the pixel intensities down to the 0-1 range and convert them to floats, by dividing by 255:
X_train, X_valid, X_test = X_train / 255., X_valid / 255., X_test / 255.
You can plot an image using Matplotlib's imshow() function, with a 'binary'
color map:
# extra code
plt.imshow(X_train[0], cmap="binary")
plt.axis('off')
plt.show()
The labels are the class IDs (represented as uint8), from 0 to 9:
y_train
array([9, 0, 0, ..., 9, 0, 2], dtype=uint8)
Here are the corresponding class names:
class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat",
"Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]
So the first image in the training set is an ankle boot:
class_names[y_train[0]]
'Ankle boot'
Let's take a look at a sample of the images in the dataset:
# extra code – this cell generates and saves Figure 10–10
n_rows = 4
n_cols = 10
plt.figure(figsize=(n_cols * 1.2, n_rows * 1.2))
for row in range(n_rows):
for col in range(n_cols):
index = n_cols * row + col
plt.subplot(n_rows, n_cols, index + 1)
plt.imshow(X_train[index], cmap="binary", interpolation="nearest")
plt.axis('off')
plt.title(class_names[y_train[index]])
plt.subplots_adjust(wspace=0.2, hspace=0.5)
save_fig("fashion_mnist_plot")
plt.show()
Creating the model using the Sequential API¶
tf.random.set_seed(42)
model = tf.keras.Sequential()
model.add(tf.keras.layers.InputLayer(input_shape=[28, 28]))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(300, activation="relu"))
model.add(tf.keras.layers.Dense(100, activation="relu"))
model.add(tf.keras.layers.Dense(10, activation="softmax"))
# extra code – clear the session to reset the name counters
tf.keras.backend.clear_session()
tf.random.set_seed(42)
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.Dense(300, activation="relu"),
tf.keras.layers.Dense(100, activation="relu"),
tf.keras.layers.Dense(10, activation="softmax")
])
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) (None, 784) 0
dense (Dense) (None, 300) 235500
dense_1 (Dense) (None, 100) 30100
dense_2 (Dense) (None, 10) 1010
=================================================================
Total params: 266,610
Trainable params: 266,610
Non-trainable params: 0
_________________________________________________________________
# extra code – another way to display the model's architecture
tf.keras.utils.plot_model(model, "my_fashion_mnist_model.png", show_shapes=True)
model.layers
[<keras.layers.core.flatten.Flatten at 0x7fb220f4d430>, <keras.layers.core.dense.Dense at 0x7fb282285af0>, <keras.layers.core.dense.Dense at 0x7fb282365b50>, <keras.layers.core.dense.Dense at 0x7fb282365fa0>]
hidden1 = model.layers[1]
hidden1.name
'dense'
model.get_layer('dense') is hidden1
True
weights, biases = hidden1.get_weights()
weights
array([[ 0.02448617, -0.00877795, -0.02189048, ..., -0.02766046,
0.03859074, -0.06889391],
[ 0.00476504, -0.03105379, -0.0586676 , ..., 0.00602964,
-0.02763776, -0.04165364],
[-0.06189284, -0.06901957, 0.07102345, ..., -0.04238207,
0.07121518, -0.07331658],
...,
[-0.03048757, 0.02155137, -0.05400612, ..., -0.00113463,
0.00228987, 0.05581069],
[ 0.07061854, -0.06960931, 0.07038955, ..., -0.00384101,
0.00034875, 0.02878492],
[-0.06022581, 0.01577859, -0.02585464, ..., -0.00527829,
0.00272203, -0.06793761]], dtype=float32)
weights.shape
(784, 300)
biases
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)
biases.shape
(300,)
Compiling the model¶
model.compile(loss="sparse_categorical_crossentropy",
optimizer="sgd",
metrics=["accuracy"])
This is equivalent to:
# extra code – this cell is equivalent to the previous cell
model.compile(loss=tf.keras.losses.sparse_categorical_crossentropy,
optimizer=tf.keras.optimizers.SGD(),
metrics=[tf.keras.metrics.sparse_categorical_accuracy])
# extra code – shows how to convert class ids to one-hot vectors
tf.keras.utils.to_categorical([0, 5, 1, 0], num_classes=10)
array([[1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)
Note: it's important to set num_classes when the number of classes is greater than the maximum class id in the sample.
# extra code – shows how to convert one-hot vectors to class ids
np.argmax(
[[1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[1., 0., 0., 0., 0., 0., 0., 0., 0., 0.]],
axis=1
)
array([0, 5, 1, 0])
Training and evaluating the model¶
history = model.fit(X_train, y_train, epochs=30,
validation_data=(X_valid, y_valid))
Epoch 1/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.7220 - sparse_categorical_accuracy: 0.7649 - val_loss: 0.4959 - val_sparse_categorical_accuracy: 0.8332 Epoch 2/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.4825 - sparse_categorical_accuracy: 0.8332 - val_loss: 0.4567 - val_sparse_categorical_accuracy: 0.8384 Epoch 3/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.4369 - sparse_categorical_accuracy: 0.8480 - val_loss: 0.4228 - val_sparse_categorical_accuracy: 0.8542 Epoch 4/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.4122 - sparse_categorical_accuracy: 0.8558 - val_loss: 0.3966 - val_sparse_categorical_accuracy: 0.8624 Epoch 5/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.3910 - sparse_categorical_accuracy: 0.8631 - val_loss: 0.3890 - val_sparse_categorical_accuracy: 0.8632 Epoch 6/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.3751 - sparse_categorical_accuracy: 0.8686 - val_loss: 0.3912 - val_sparse_categorical_accuracy: 0.8600 Epoch 7/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.3628 - sparse_categorical_accuracy: 0.8710 - val_loss: 0.3723 - val_sparse_categorical_accuracy: 0.8698 Epoch 8/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.3514 - sparse_categorical_accuracy: 0.8755 - val_loss: 0.3767 - val_sparse_categorical_accuracy: 0.8612 Epoch 9/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.3406 - sparse_categorical_accuracy: 0.8795 - val_loss: 0.3513 - val_sparse_categorical_accuracy: 0.8726 Epoch 10/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.3306 - sparse_categorical_accuracy: 0.8812 - val_loss: 0.3539 - val_sparse_categorical_accuracy: 0.8738 Epoch 11/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.3223 - sparse_categorical_accuracy: 0.8860 - val_loss: 0.3606 - val_sparse_categorical_accuracy: 0.8712 Epoch 12/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.3146 - sparse_categorical_accuracy: 0.8869 - val_loss: 0.3472 - val_sparse_categorical_accuracy: 0.8742 Epoch 13/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.3071 - sparse_categorical_accuracy: 0.8900 - val_loss: 0.3284 - val_sparse_categorical_accuracy: 0.8800 Epoch 14/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.3001 - sparse_categorical_accuracy: 0.8922 - val_loss: 0.3413 - val_sparse_categorical_accuracy: 0.8780 Epoch 15/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2938 - sparse_categorical_accuracy: 0.8945 - val_loss: 0.3376 - val_sparse_categorical_accuracy: 0.8822 Epoch 16/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2867 - sparse_categorical_accuracy: 0.8971 - val_loss: 0.3272 - val_sparse_categorical_accuracy: 0.8796 Epoch 17/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2822 - sparse_categorical_accuracy: 0.8978 - val_loss: 0.3317 - val_sparse_categorical_accuracy: 0.8796 Epoch 18/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2757 - sparse_categorical_accuracy: 0.9001 - val_loss: 0.3240 - val_sparse_categorical_accuracy: 0.8824 Epoch 19/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2711 - sparse_categorical_accuracy: 0.9030 - val_loss: 0.3484 - val_sparse_categorical_accuracy: 0.8720 Epoch 20/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2662 - sparse_categorical_accuracy: 0.9045 - val_loss: 0.3209 - val_sparse_categorical_accuracy: 0.8800 Epoch 21/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2613 - sparse_categorical_accuracy: 0.9046 - val_loss: 0.3178 - val_sparse_categorical_accuracy: 0.8862 Epoch 22/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2563 - sparse_categorical_accuracy: 0.9069 - val_loss: 0.3122 - val_sparse_categorical_accuracy: 0.8848 Epoch 23/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2520 - sparse_categorical_accuracy: 0.9098 - val_loss: 0.3480 - val_sparse_categorical_accuracy: 0.8716 Epoch 24/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2469 - sparse_categorical_accuracy: 0.9113 - val_loss: 0.3202 - val_sparse_categorical_accuracy: 0.8878 Epoch 25/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2428 - sparse_categorical_accuracy: 0.9123 - val_loss: 0.3152 - val_sparse_categorical_accuracy: 0.8856 Epoch 26/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2393 - sparse_categorical_accuracy: 0.9143 - val_loss: 0.3102 - val_sparse_categorical_accuracy: 0.8852 Epoch 27/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2341 - sparse_categorical_accuracy: 0.9147 - val_loss: 0.3200 - val_sparse_categorical_accuracy: 0.8850 Epoch 28/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2313 - sparse_categorical_accuracy: 0.9169 - val_loss: 0.3100 - val_sparse_categorical_accuracy: 0.8900 Epoch 29/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2268 - sparse_categorical_accuracy: 0.9185 - val_loss: 0.3215 - val_sparse_categorical_accuracy: 0.8864 Epoch 30/30 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2235 - sparse_categorical_accuracy: 0.9200 - val_loss: 0.3056 - val_sparse_categorical_accuracy: 0.8894
history.params
{'verbose': 1, 'epochs': 30, 'steps': 1719}
print(history.epoch)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29]
import matplotlib.pyplot as plt
import pandas as pd
pd.DataFrame(history.history).plot(
figsize=(8, 5), xlim=[0, 29], ylim=[0, 1], grid=True, xlabel="Epoch",
style=["r--", "r--.", "b-", "b-*"])
plt.legend(loc="lower left") # extra code
save_fig("keras_learning_curves_plot") # extra code
plt.show()
# extra code – shows how to shift the training curve by -1/2 epoch
plt.figure(figsize=(8, 5))
for key, style in zip(history.history, ["r--", "r--.", "b-", "b-*"]):
epochs = np.array(history.epoch) + (0 if key.startswith("val_") else -0.5)
plt.plot(epochs, history.history[key], style, label=key)
plt.xlabel("Epoch")
plt.axis([-0.5, 29, 0., 1])
plt.legend(loc="lower left")
plt.grid()
plt.show()
model.evaluate(X_test, y_test)
313/313 [==============================] - 0s 867us/step - loss: 0.3243 - sparse_categorical_accuracy: 0.8864
[0.32431697845458984, 0.8863999843597412]
Using the model to make predictions¶
X_new = X_test[:3]
y_proba = model.predict(X_new)
y_proba.round(2)
array([[0. , 0. , 0. , 0. , 0. , 0.01, 0. , 0.02, 0. , 0.97],
[0. , 0. , 0.99, 0. , 0.01, 0. , 0. , 0. , 0. , 0. ],
[0. , 1. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ]],
dtype=float32)
y_pred = y_proba.argmax(axis=-1)
y_pred
array([9, 2, 1])
np.array(class_names)[y_pred]
array(['Ankle boot', 'Pullover', 'Trouser'], dtype='<U11')
y_new = y_test[:3]
y_new
array([9, 2, 1], dtype=uint8)
# extra code – this cell generates and saves Figure 10–12
plt.figure(figsize=(7.2, 2.4))
for index, image in enumerate(X_new):
plt.subplot(1, 3, index + 1)
plt.imshow(image, cmap="binary", interpolation="nearest")
plt.axis('off')
plt.title(class_names[y_test[index]])
plt.subplots_adjust(wspace=0.2, hspace=0.5)
save_fig('fashion_mnist_images_plot', tight_layout=False)
plt.show()
Building a Regression MLP Using the Sequential API¶
Let's load, split and scale the California housing dataset (the original one, not the modified one as in chapter 2):
# extra code – load and split the California housing dataset, like earlier
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(
housing.data, housing.target, random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train_full, y_train_full, random_state=42)
tf.random.set_seed(42)
norm_layer = tf.keras.layers.Normalization(input_shape=X_train.shape[1:])
model = tf.keras.Sequential([
norm_layer,
tf.keras.layers.Dense(50, activation="relu"),
tf.keras.layers.Dense(50, activation="relu"),
tf.keras.layers.Dense(50, activation="relu"),
tf.keras.layers.Dense(1)
])
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
model.compile(loss="mse", optimizer=optimizer, metrics=["RootMeanSquaredError"])
norm_layer.adapt(X_train)
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
mse_test, rmse_test = model.evaluate(X_test, y_test)
X_new = X_test[:3]
y_pred = model.predict(X_new)
Epoch 1/20 363/363 [==============================] - 1s 1ms/step - loss: 0.9051 - root_mean_squared_error: 0.9514 - val_loss: 0.4030 - val_root_mean_squared_error: 0.6348 Epoch 2/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3843 - root_mean_squared_error: 0.6199 - val_loss: 0.8436 - val_root_mean_squared_error: 0.9185 Epoch 3/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3609 - root_mean_squared_error: 0.6007 - val_loss: 0.3744 - val_root_mean_squared_error: 0.6119 Epoch 4/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3416 - root_mean_squared_error: 0.5844 - val_loss: 0.4343 - val_root_mean_squared_error: 0.6590 Epoch 5/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3301 - root_mean_squared_error: 0.5746 - val_loss: 0.3085 - val_root_mean_squared_error: 0.5554 Epoch 6/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3168 - root_mean_squared_error: 0.5629 - val_loss: 0.4544 - val_root_mean_squared_error: 0.6741 Epoch 7/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3162 - root_mean_squared_error: 0.5623 - val_loss: 0.2941 - val_root_mean_squared_error: 0.5423 Epoch 8/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3045 - root_mean_squared_error: 0.5518 - val_loss: 0.3333 - val_root_mean_squared_error: 0.5773 Epoch 9/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2974 - root_mean_squared_error: 0.5453 - val_loss: 0.3446 - val_root_mean_squared_error: 0.5870 Epoch 10/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2921 - root_mean_squared_error: 0.5404 - val_loss: 0.2874 - val_root_mean_squared_error: 0.5361 Epoch 11/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2863 - root_mean_squared_error: 0.5351 - val_loss: 0.4141 - val_root_mean_squared_error: 0.6435 Epoch 12/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2942 - root_mean_squared_error: 0.5424 - val_loss: 1.0956 - val_root_mean_squared_error: 1.0467 Epoch 13/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2864 - root_mean_squared_error: 0.5352 - val_loss: 0.3063 - val_root_mean_squared_error: 0.5534 Epoch 14/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2804 - root_mean_squared_error: 0.5295 - val_loss: 0.2709 - val_root_mean_squared_error: 0.5205 Epoch 15/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2784 - root_mean_squared_error: 0.5276 - val_loss: 0.3680 - val_root_mean_squared_error: 0.6066 Epoch 16/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2757 - root_mean_squared_error: 0.5250 - val_loss: 0.2730 - val_root_mean_squared_error: 0.5225 Epoch 17/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2739 - root_mean_squared_error: 0.5234 - val_loss: 0.3668 - val_root_mean_squared_error: 0.6056 Epoch 18/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2694 - root_mean_squared_error: 0.5191 - val_loss: 0.4188 - val_root_mean_squared_error: 0.6472 Epoch 19/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2677 - root_mean_squared_error: 0.5174 - val_loss: 0.9663 - val_root_mean_squared_error: 0.9830 Epoch 20/20 363/363 [==============================] - 0s 1ms/step - loss: 0.2755 - root_mean_squared_error: 0.5249 - val_loss: 0.2978 - val_root_mean_squared_error: 0.5457 162/162 [==============================] - 0s 508us/step - loss: 0.2806 - root_mean_squared_error: 0.5297
rmse_test
0.5297096967697144
y_pred
array([[0.4969182],
[1.195265 ],
[4.9428763]], dtype=float32)
Building Complex Models Using the Functional API¶
Not all neural network models are simply sequential. Some may have complex topologies. Some may have multiple inputs and/or multiple outputs. For example, a Wide & Deep neural network (see paper) connects all or part of the inputs directly to the output layer.
# extra code – reset the name counters and make the code reproducible
tf.keras.backend.clear_session()
tf.random.set_seed(42)
normalization_layer = tf.keras.layers.Normalization()
hidden_layer1 = tf.keras.layers.Dense(30, activation="relu")
hidden_layer2 = tf.keras.layers.Dense(30, activation="relu")
concat_layer = tf.keras.layers.Concatenate()
output_layer = tf.keras.layers.Dense(1)
input_ = tf.keras.layers.Input(shape=X_train.shape[1:])
normalized = normalization_layer(input_)
hidden1 = hidden_layer1(normalized)
hidden2 = hidden_layer2(hidden1)
concat = concat_layer([normalized, hidden2])
output = output_layer(concat)
model = tf.keras.Model(inputs=[input_], outputs=[output])
model.summary()
Model: "model"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) [(None, 8)] 0 []
normalization (Normalization) (None, 8) 17 ['input_1[0][0]']
dense (Dense) (None, 30) 270 ['normalization[0][0]']
dense_1 (Dense) (None, 30) 930 ['dense[0][0]']
concatenate (Concatenate) (None, 38) 0 ['input_1[0][0]',
'dense_1[0][0]']
dense_2 (Dense) (None, 1) 39 ['concatenate[0][0]']
==================================================================================================
Total params: 1,256
Trainable params: 1,239
Non-trainable params: 17
__________________________________________________________________________________________________
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
model.compile(loss="mse", optimizer=optimizer, metrics=["RootMeanSquaredError"])
normalization_layer.adapt(X_train)
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
y_pred = model.predict(X_new)
Epoch 1/20 363/363 [==============================] - 1s 1ms/step - loss: 122.3226 - root_mean_squared_error: 11.0600 - val_loss: 305.9134 - val_root_mean_squared_error: 17.4904 Epoch 2/20 363/363 [==============================] - 0s 1ms/step - loss: 5.5425 - root_mean_squared_error: 2.3543 - val_loss: 183.4622 - val_root_mean_squared_error: 13.5448 Epoch 3/20 363/363 [==============================] - 0s 979us/step - loss: 3.0631 - root_mean_squared_error: 1.7502 - val_loss: 87.2228 - val_root_mean_squared_error: 9.3393 Epoch 4/20 363/363 [==============================] - 0s 1ms/step - loss: 1.5796 - root_mean_squared_error: 1.2568 - val_loss: 35.3699 - val_root_mean_squared_error: 5.9473 Epoch 5/20 363/363 [==============================] - 0s 1ms/step - loss: 0.9536 - root_mean_squared_error: 0.9765 - val_loss: 12.3882 - val_root_mean_squared_error: 3.5197 Epoch 6/20 363/363 [==============================] - 0s 1ms/step - loss: 0.6322 - root_mean_squared_error: 0.7951 - val_loss: 4.1676 - val_root_mean_squared_error: 2.0415 Epoch 7/20 363/363 [==============================] - 0s 1ms/step - loss: 0.5069 - root_mean_squared_error: 0.7120 - val_loss: 1.2937 - val_root_mean_squared_error: 1.1374 Epoch 8/20 363/363 [==============================] - 0s 980us/step - loss: 0.4525 - root_mean_squared_error: 0.6727 - val_loss: 0.4837 - val_root_mean_squared_error: 0.6955 Epoch 9/20 363/363 [==============================] - 0s 1ms/step - loss: 0.4293 - root_mean_squared_error: 0.6552 - val_loss: 0.4343 - val_root_mean_squared_error: 0.6590 Epoch 10/20 363/363 [==============================] - 0s 962us/step - loss: 0.4120 - root_mean_squared_error: 0.6419 - val_loss: 0.3996 - val_root_mean_squared_error: 0.6321 Epoch 11/20 363/363 [==============================] - 0s 988us/step - loss: 0.4203 - root_mean_squared_error: 0.6483 - val_loss: 0.4149 - val_root_mean_squared_error: 0.6441 Epoch 12/20 363/363 [==============================] - 0s 952us/step - loss: 0.3916 - root_mean_squared_error: 0.6257 - val_loss: 0.4569 - val_root_mean_squared_error: 0.6759 Epoch 13/20 363/363 [==============================] - 0s 957us/step - loss: 0.4147 - root_mean_squared_error: 0.6440 - val_loss: 0.3736 - val_root_mean_squared_error: 0.6113 Epoch 14/20 363/363 [==============================] - 0s 949us/step - loss: 0.3824 - root_mean_squared_error: 0.6184 - val_loss: 0.4550 - val_root_mean_squared_error: 0.6745 Epoch 15/20 363/363 [==============================] - 0s 982us/step - loss: 0.4003 - root_mean_squared_error: 0.6327 - val_loss: 0.8553 - val_root_mean_squared_error: 0.9248 Epoch 16/20 363/363 [==============================] - 0s 960us/step - loss: 0.4245 - root_mean_squared_error: 0.6516 - val_loss: 1.9204 - val_root_mean_squared_error: 1.3858 Epoch 17/20 363/363 [==============================] - 0s 987us/step - loss: 0.4580 - root_mean_squared_error: 0.6767 - val_loss: 2.0632 - val_root_mean_squared_error: 1.4364 Epoch 18/20 363/363 [==============================] - 0s 961us/step - loss: 0.4692 - root_mean_squared_error: 0.6850 - val_loss: 3.5730 - val_root_mean_squared_error: 1.8902 Epoch 19/20 363/363 [==============================] - 0s 1ms/step - loss: 0.4367 - root_mean_squared_error: 0.6608 - val_loss: 3.9989 - val_root_mean_squared_error: 1.9997 Epoch 20/20 363/363 [==============================] - 0s 1ms/step - loss: 0.4683 - root_mean_squared_error: 0.6843 - val_loss: 2.2966 - val_root_mean_squared_error: 1.5155 162/162 [==============================] - 0s 612us/step - loss: 0.5723 - root_mean_squared_error: 0.7565
What if you want to send different subsets of input features through the wide or deep paths? We will send 5 features (features 0 to 4), and 6 through the deep path (features 2 to 7). Note that 3 features will go through both (features 2, 3 and 4).
tf.random.set_seed(42) # extra code
input_wide = tf.keras.layers.Input(shape=[5]) # features 0 to 4
input_deep = tf.keras.layers.Input(shape=[6]) # features 2 to 7
norm_layer_wide = tf.keras.layers.Normalization()
norm_layer_deep = tf.keras.layers.Normalization()
norm_wide = norm_layer_wide(input_wide)
norm_deep = norm_layer_deep(input_deep)
hidden1 = tf.keras.layers.Dense(30, activation="relu")(norm_deep)
hidden2 = tf.keras.layers.Dense(30, activation="relu")(hidden1)
concat = tf.keras.layers.concatenate([norm_wide, hidden2])
output = tf.keras.layers.Dense(1)(concat)
model = tf.keras.Model(inputs=[input_wide, input_deep], outputs=[output])
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
model.compile(loss="mse", optimizer=optimizer, metrics=["RootMeanSquaredError"])
X_train_wide, X_train_deep = X_train[:, :5], X_train[:, 2:]
X_valid_wide, X_valid_deep = X_valid[:, :5], X_valid[:, 2:]
X_test_wide, X_test_deep = X_test[:, :5], X_test[:, 2:]
X_new_wide, X_new_deep = X_test_wide[:3], X_test_deep[:3]
norm_layer_wide.adapt(X_train_wide)
norm_layer_deep.adapt(X_train_deep)
history = model.fit((X_train_wide, X_train_deep), y_train, epochs=20,
validation_data=((X_valid_wide, X_valid_deep), y_valid))
mse_test = model.evaluate((X_test_wide, X_test_deep), y_test)
y_pred = model.predict((X_new_wide, X_new_deep))
Epoch 1/20 363/363 [==============================] - 1s 2ms/step - loss: 1.2768 - root_mean_squared_error: 1.1300 - val_loss: 0.9497 - val_root_mean_squared_error: 0.9745 Epoch 2/20 363/363 [==============================] - 0s 1ms/step - loss: 0.4767 - root_mean_squared_error: 0.6904 - val_loss: 1.4311 - val_root_mean_squared_error: 1.1963 Epoch 3/20 363/363 [==============================] - 0s 1ms/step - loss: 0.4433 - root_mean_squared_error: 0.6658 - val_loss: 0.4258 - val_root_mean_squared_error: 0.6525 Epoch 4/20 363/363 [==============================] - 0s 1ms/step - loss: 0.4057 - root_mean_squared_error: 0.6370 - val_loss: 0.4016 - val_root_mean_squared_error: 0.6338 Epoch 5/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3940 - root_mean_squared_error: 0.6277 - val_loss: 1.4914 - val_root_mean_squared_error: 1.2212 Epoch 6/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3873 - root_mean_squared_error: 0.6224 - val_loss: 2.6759 - val_root_mean_squared_error: 1.6358 Epoch 7/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3914 - root_mean_squared_error: 0.6257 - val_loss: 3.0592 - val_root_mean_squared_error: 1.7490 Epoch 8/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3735 - root_mean_squared_error: 0.6112 - val_loss: 3.3043 - val_root_mean_squared_error: 1.8178 Epoch 9/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3712 - root_mean_squared_error: 0.6093 - val_loss: 2.1298 - val_root_mean_squared_error: 1.4594 Epoch 10/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3693 - root_mean_squared_error: 0.6077 - val_loss: 1.7402 - val_root_mean_squared_error: 1.3192 Epoch 11/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3578 - root_mean_squared_error: 0.5982 - val_loss: 0.6127 - val_root_mean_squared_error: 0.7827 Epoch 12/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3605 - root_mean_squared_error: 0.6005 - val_loss: 1.3970 - val_root_mean_squared_error: 1.1819 Epoch 13/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3527 - root_mean_squared_error: 0.5939 - val_loss: 0.9449 - val_root_mean_squared_error: 0.9721 Epoch 14/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3436 - root_mean_squared_error: 0.5861 - val_loss: 0.7757 - val_root_mean_squared_error: 0.8807 Epoch 15/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3421 - root_mean_squared_error: 0.5849 - val_loss: 0.8920 - val_root_mean_squared_error: 0.9445 Epoch 16/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3405 - root_mean_squared_error: 0.5835 - val_loss: 0.9334 - val_root_mean_squared_error: 0.9661 Epoch 17/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3394 - root_mean_squared_error: 0.5826 - val_loss: 1.3433 - val_root_mean_squared_error: 1.1590 Epoch 18/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3384 - root_mean_squared_error: 0.5817 - val_loss: 2.6406 - val_root_mean_squared_error: 1.6250 Epoch 19/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3459 - root_mean_squared_error: 0.5881 - val_loss: 2.2482 - val_root_mean_squared_error: 1.4994 Epoch 20/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3503 - root_mean_squared_error: 0.5919 - val_loss: 1.4407 - val_root_mean_squared_error: 1.2003 162/162 [==============================] - 0s 672us/step - loss: 0.3388 - root_mean_squared_error: 0.5821
Adding an auxiliary output for regularization:
tf.keras.backend.clear_session()
tf.random.set_seed(42)
input_wide = tf.keras.layers.Input(shape=[5]) # features 0 to 4
input_deep = tf.keras.layers.Input(shape=[6]) # features 2 to 7
norm_layer_wide = tf.keras.layers.Normalization()
norm_layer_deep = tf.keras.layers.Normalization()
norm_wide = norm_layer_wide(input_wide)
norm_deep = norm_layer_deep(input_deep)
hidden1 = tf.keras.layers.Dense(30, activation="relu")(norm_deep)
hidden2 = tf.keras.layers.Dense(30, activation="relu")(hidden1)
concat = tf.keras.layers.concatenate([norm_wide, hidden2])
output = tf.keras.layers.Dense(1)(concat)
aux_output = tf.keras.layers.Dense(1)(hidden2)
model = tf.keras.Model(inputs=[input_wide, input_deep],
outputs=[output, aux_output])
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
model.compile(loss=("mse", "mse"), loss_weights=(0.9, 0.1), optimizer=optimizer,
metrics=["RootMeanSquaredError"])
norm_layer_wide.adapt(X_train_wide)
norm_layer_deep.adapt(X_train_deep)
history = model.fit(
(X_train_wide, X_train_deep), (y_train, y_train), epochs=20,
validation_data=((X_valid_wide, X_valid_deep), (y_valid, y_valid))
)
Epoch 1/20 363/363 [==============================] - 1s 2ms/step - loss: 1.3490 - dense_2_loss: 1.2742 - dense_3_loss: 2.0215 - dense_2_root_mean_squared_error: 1.1288 - dense_3_root_mean_squared_error: 1.4218 - val_loss: 1.5415 - val_dense_2_loss: 0.9593 - val_dense_3_loss: 6.7806 - val_dense_2_root_mean_squared_error: 0.9795 - val_dense_3_root_mean_squared_error: 2.6040 Epoch 2/20 363/363 [==============================] - 0s 1ms/step - loss: 0.5101 - dense_2_loss: 0.4785 - dense_3_loss: 0.7952 - dense_2_root_mean_squared_error: 0.6917 - dense_3_root_mean_squared_error: 0.8917 - val_loss: 1.3624 - val_dense_2_loss: 1.0094 - val_dense_3_loss: 4.5401 - val_dense_2_root_mean_squared_error: 1.0047 - val_dense_3_root_mean_squared_error: 2.1307 Epoch 3/20 363/363 [==============================] - 0s 1ms/step - loss: 0.4618 - dense_2_loss: 0.4404 - dense_3_loss: 0.6546 - dense_2_root_mean_squared_error: 0.6636 - dense_3_root_mean_squared_error: 0.8091 - val_loss: 0.5361 - val_dense_2_loss: 0.3975 - val_dense_3_loss: 1.7837 - val_dense_2_root_mean_squared_error: 0.6305 - val_dense_3_root_mean_squared_error: 1.3356 Epoch 4/20 363/363 [==============================] - 0s 1ms/step - loss: 0.4252 - dense_2_loss: 0.4059 - dense_3_loss: 0.5985 - dense_2_root_mean_squared_error: 0.6371 - dense_3_root_mean_squared_error: 0.7736 - val_loss: 0.5182 - val_dense_2_loss: 0.4590 - val_dense_3_loss: 1.0517 - val_dense_2_root_mean_squared_error: 0.6775 - val_dense_3_root_mean_squared_error: 1.0255 Epoch 5/20 363/363 [==============================] - 0s 1ms/step - loss: 0.4106 - dense_2_loss: 0.3931 - dense_3_loss: 0.5690 - dense_2_root_mean_squared_error: 0.6269 - dense_3_root_mean_squared_error: 0.7543 - val_loss: 0.4049 - val_dense_2_loss: 0.3588 - val_dense_3_loss: 0.8196 - val_dense_2_root_mean_squared_error: 0.5990 - val_dense_3_root_mean_squared_error: 0.9053 Epoch 6/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3944 - dense_2_loss: 0.3780 - dense_3_loss: 0.5424 - dense_2_root_mean_squared_error: 0.6148 - dense_3_root_mean_squared_error: 0.7365 - val_loss: 0.4168 - val_dense_2_loss: 0.3934 - val_dense_3_loss: 0.6275 - val_dense_2_root_mean_squared_error: 0.6272 - val_dense_3_root_mean_squared_error: 0.7921 Epoch 7/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3837 - dense_2_loss: 0.3694 - dense_3_loss: 0.5126 - dense_2_root_mean_squared_error: 0.6078 - dense_3_root_mean_squared_error: 0.7160 - val_loss: 0.3661 - val_dense_2_loss: 0.3430 - val_dense_3_loss: 0.5747 - val_dense_2_root_mean_squared_error: 0.5856 - val_dense_3_root_mean_squared_error: 0.7581 Epoch 8/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3731 - dense_2_loss: 0.3608 - dense_3_loss: 0.4840 - dense_2_root_mean_squared_error: 0.6007 - dense_3_root_mean_squared_error: 0.6957 - val_loss: 0.8555 - val_dense_2_loss: 0.8704 - val_dense_3_loss: 0.7218 - val_dense_2_root_mean_squared_error: 0.9330 - val_dense_3_root_mean_squared_error: 0.8496 Epoch 9/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3672 - dense_2_loss: 0.3567 - dense_3_loss: 0.4624 - dense_2_root_mean_squared_error: 0.5972 - dense_3_root_mean_squared_error: 0.6800 - val_loss: 2.6877 - val_dense_2_loss: 2.9011 - val_dense_3_loss: 0.7675 - val_dense_2_root_mean_squared_error: 1.7033 - val_dense_3_root_mean_squared_error: 0.8761 Epoch 10/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3837 - dense_2_loss: 0.3765 - dense_3_loss: 0.4481 - dense_2_root_mean_squared_error: 0.6136 - dense_3_root_mean_squared_error: 0.6694 - val_loss: 3.6017 - val_dense_2_loss: 3.8004 - val_dense_3_loss: 1.8132 - val_dense_2_root_mean_squared_error: 1.9495 - val_dense_3_root_mean_squared_error: 1.3466 Epoch 11/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3728 - dense_2_loss: 0.3656 - dense_3_loss: 0.4377 - dense_2_root_mean_squared_error: 0.6046 - dense_3_root_mean_squared_error: 0.6616 - val_loss: 0.6115 - val_dense_2_loss: 0.6325 - val_dense_3_loss: 0.4226 - val_dense_2_root_mean_squared_error: 0.7953 - val_dense_3_root_mean_squared_error: 0.6501 Epoch 12/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3750 - dense_2_loss: 0.3688 - dense_3_loss: 0.4303 - dense_2_root_mean_squared_error: 0.6073 - dense_3_root_mean_squared_error: 0.6560 - val_loss: 0.9371 - val_dense_2_loss: 0.9545 - val_dense_3_loss: 0.7799 - val_dense_2_root_mean_squared_error: 0.9770 - val_dense_3_root_mean_squared_error: 0.8831 Epoch 13/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3570 - dense_2_loss: 0.3499 - dense_3_loss: 0.4203 - dense_2_root_mean_squared_error: 0.5915 - dense_3_root_mean_squared_error: 0.6483 - val_loss: 0.4224 - val_dense_2_loss: 0.4245 - val_dense_3_loss: 0.4039 - val_dense_2_root_mean_squared_error: 0.6515 - val_dense_3_root_mean_squared_error: 0.6355 Epoch 14/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3493 - dense_2_loss: 0.3421 - dense_3_loss: 0.4148 - dense_2_root_mean_squared_error: 0.5849 - dense_3_root_mean_squared_error: 0.6440 - val_loss: 0.3410 - val_dense_2_loss: 0.3221 - val_dense_3_loss: 0.5105 - val_dense_2_root_mean_squared_error: 0.5676 - val_dense_3_root_mean_squared_error: 0.7145 Epoch 15/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3496 - dense_2_loss: 0.3432 - dense_3_loss: 0.4076 - dense_2_root_mean_squared_error: 0.5858 - dense_3_root_mean_squared_error: 0.6384 - val_loss: 0.6461 - val_dense_2_loss: 0.6671 - val_dense_3_loss: 0.4570 - val_dense_2_root_mean_squared_error: 0.8168 - val_dense_3_root_mean_squared_error: 0.6760 Epoch 16/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3435 - dense_2_loss: 0.3370 - dense_3_loss: 0.4022 - dense_2_root_mean_squared_error: 0.5805 - dense_3_root_mean_squared_error: 0.6342 - val_loss: 0.6875 - val_dense_2_loss: 0.6841 - val_dense_3_loss: 0.7182 - val_dense_2_root_mean_squared_error: 0.8271 - val_dense_3_root_mean_squared_error: 0.8475 Epoch 17/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3458 - dense_2_loss: 0.3393 - dense_3_loss: 0.4037 - dense_2_root_mean_squared_error: 0.5825 - dense_3_root_mean_squared_error: 0.6354 - val_loss: 1.1564 - val_dense_2_loss: 1.2129 - val_dense_3_loss: 0.6483 - val_dense_2_root_mean_squared_error: 1.1013 - val_dense_3_root_mean_squared_error: 0.8052 Epoch 18/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3446 - dense_2_loss: 0.3385 - dense_3_loss: 0.3994 - dense_2_root_mean_squared_error: 0.5818 - dense_3_root_mean_squared_error: 0.6320 - val_loss: 3.9325 - val_dense_2_loss: 4.0947 - val_dense_3_loss: 2.4722 - val_dense_2_root_mean_squared_error: 2.0235 - val_dense_3_root_mean_squared_error: 1.5723 Epoch 19/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3563 - dense_2_loss: 0.3511 - dense_3_loss: 0.4029 - dense_2_root_mean_squared_error: 0.5925 - dense_3_root_mean_squared_error: 0.6347 - val_loss: 1.4560 - val_dense_2_loss: 1.5433 - val_dense_3_loss: 0.6697 - val_dense_2_root_mean_squared_error: 1.2423 - val_dense_3_root_mean_squared_error: 0.8183 Epoch 20/20 363/363 [==============================] - 0s 1ms/step - loss: 0.3546 - dense_2_loss: 0.3498 - dense_3_loss: 0.3981 - dense_2_root_mean_squared_error: 0.5914 - dense_3_root_mean_squared_error: 0.6310 - val_loss: 1.1709 - val_dense_2_loss: 1.1945 - val_dense_3_loss: 0.9589 - val_dense_2_root_mean_squared_error: 1.0929 - val_dense_3_root_mean_squared_error: 0.9792
eval_results = model.evaluate((X_test_wide, X_test_deep), (y_test, y_test))
weighted_sum_of_losses, main_loss, aux_loss, main_rmse, aux_rmse = eval_results
162/162 [==============================] - 0s 778us/step - loss: 0.3446 - dense_2_loss: 0.3381 - dense_3_loss: 0.4031 - dense_2_root_mean_squared_error: 0.5815 - dense_3_root_mean_squared_error: 0.6349
y_pred_main, y_pred_aux = model.predict((X_new_wide, X_new_deep))
WARNING:tensorflow:5 out of the last 5 calls to <function Model.make_predict_function.<locals>.predict_function at 0x7fb250e69310> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
y_pred_tuple = model.predict((X_new_wide, X_new_deep))
y_pred = dict(zip(model.output_names, y_pred_tuple))
Using the Subclassing API to Build Dynamic Models¶
class WideAndDeepModel(tf.keras.Model):
def __init__(self, units=30, activation="relu", **kwargs):
super().__init__(**kwargs) # needed to support naming the model
self.norm_layer_wide = tf.keras.layers.Normalization()
self.norm_layer_deep = tf.keras.layers.Normalization()
self.hidden1 = tf.keras.layers.Dense(units, activation=activation)
self.hidden2 = tf.keras.layers.Dense(units, activation=activation)
self.main_output = tf.keras.layers.Dense(1)
self.aux_output = tf.keras.layers.Dense(1)
def call(self, inputs):
input_wide, input_deep = inputs
norm_wide = self.norm_layer_wide(input_wide)
norm_deep = self.norm_layer_deep(input_deep)
hidden1 = self.hidden1(norm_deep)
hidden2 = self.hidden2(hidden1)
concat = tf.keras.layers.concatenate([norm_wide, hidden2])
output = self.main_output(concat)
aux_output = self.aux_output(hidden2)
return output, aux_output
tf.random.set_seed(42) # extra code – just for reproducibility
model = WideAndDeepModel(30, activation="relu", name="my_cool_model")
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
model.compile(loss="mse", loss_weights=[0.9, 0.1], optimizer=optimizer,
metrics=["RootMeanSquaredError"])
model.norm_layer_wide.adapt(X_train_wide)
model.norm_layer_deep.adapt(X_train_deep)
history = model.fit(
(X_train_wide, X_train_deep), (y_train, y_train), epochs=10,
validation_data=((X_valid_wide, X_valid_deep), (y_valid, y_valid)))
eval_results = model.evaluate((X_test_wide, X_test_deep), (y_test, y_test))
weighted_sum_of_losses, main_loss, aux_loss, main_rmse, aux_rmse = eval_results
y_pred_main, y_pred_aux = model.predict((X_new_wide, X_new_deep))
Epoch 1/10 363/363 [==============================] - 1s 2ms/step - loss: 1.3490 - output_1_loss: 1.2742 - output_2_loss: 2.0215 - output_1_root_mean_squared_error: 1.1288 - output_2_root_mean_squared_error: 1.4218 - val_loss: 1.5415 - val_output_1_loss: 0.9593 - val_output_2_loss: 6.7806 - val_output_1_root_mean_squared_error: 0.9795 - val_output_2_root_mean_squared_error: 2.6040 Epoch 2/10 363/363 [==============================] - 0s 1ms/step - loss: 0.5101 - output_1_loss: 0.4785 - output_2_loss: 0.7952 - output_1_root_mean_squared_error: 0.6917 - output_2_root_mean_squared_error: 0.8917 - val_loss: 1.3624 - val_output_1_loss: 1.0094 - val_output_2_loss: 4.5401 - val_output_1_root_mean_squared_error: 1.0047 - val_output_2_root_mean_squared_error: 2.1307 Epoch 3/10 363/363 [==============================] - 0s 1ms/step - loss: 0.4618 - output_1_loss: 0.4404 - output_2_loss: 0.6546 - output_1_root_mean_squared_error: 0.6636 - output_2_root_mean_squared_error: 0.8091 - val_loss: 0.5361 - val_output_1_loss: 0.3975 - val_output_2_loss: 1.7837 - val_output_1_root_mean_squared_error: 0.6305 - val_output_2_root_mean_squared_error: 1.3356 Epoch 4/10 363/363 [==============================] - 0s 1ms/step - loss: 0.4252 - output_1_loss: 0.4059 - output_2_loss: 0.5985 - output_1_root_mean_squared_error: 0.6371 - output_2_root_mean_squared_error: 0.7736 - val_loss: 0.5182 - val_output_1_loss: 0.4590 - val_output_2_loss: 1.0517 - val_output_1_root_mean_squared_error: 0.6775 - val_output_2_root_mean_squared_error: 1.0255 Epoch 5/10 363/363 [==============================] - 0s 1ms/step - loss: 0.4106 - output_1_loss: 0.3931 - output_2_loss: 0.5690 - output_1_root_mean_squared_error: 0.6269 - output_2_root_mean_squared_error: 0.7543 - val_loss: 0.4049 - val_output_1_loss: 0.3588 - val_output_2_loss: 0.8196 - val_output_1_root_mean_squared_error: 0.5990 - val_output_2_root_mean_squared_error: 0.9053 Epoch 6/10 363/363 [==============================] - 0s 1ms/step - loss: 0.3944 - output_1_loss: 0.3780 - output_2_loss: 0.5424 - output_1_root_mean_squared_error: 0.6148 - output_2_root_mean_squared_error: 0.7365 - val_loss: 0.4168 - val_output_1_loss: 0.3934 - val_output_2_loss: 0.6275 - val_output_1_root_mean_squared_error: 0.6272 - val_output_2_root_mean_squared_error: 0.7921 Epoch 7/10 363/363 [==============================] - 0s 1ms/step - loss: 0.3837 - output_1_loss: 0.3694 - output_2_loss: 0.5126 - output_1_root_mean_squared_error: 0.6078 - output_2_root_mean_squared_error: 0.7160 - val_loss: 0.3661 - val_output_1_loss: 0.3430 - val_output_2_loss: 0.5747 - val_output_1_root_mean_squared_error: 0.5856 - val_output_2_root_mean_squared_error: 0.7581 Epoch 8/10 363/363 [==============================] - 0s 1ms/step - loss: 0.3731 - output_1_loss: 0.3608 - output_2_loss: 0.4840 - output_1_root_mean_squared_error: 0.6007 - output_2_root_mean_squared_error: 0.6957 - val_loss: 0.8555 - val_output_1_loss: 0.8704 - val_output_2_loss: 0.7218 - val_output_1_root_mean_squared_error: 0.9330 - val_output_2_root_mean_squared_error: 0.8496 Epoch 9/10 363/363 [==============================] - 0s 1ms/step - loss: 0.3672 - output_1_loss: 0.3567 - output_2_loss: 0.4624 - output_1_root_mean_squared_error: 0.5972 - output_2_root_mean_squared_error: 0.6800 - val_loss: 2.6877 - val_output_1_loss: 2.9011 - val_output_2_loss: 0.7675 - val_output_1_root_mean_squared_error: 1.7033 - val_output_2_root_mean_squared_error: 0.8761 Epoch 10/10 363/363 [==============================] - 0s 1ms/step - loss: 0.3837 - output_1_loss: 0.3765 - output_2_loss: 0.4481 - output_1_root_mean_squared_error: 0.6136 - output_2_root_mean_squared_error: 0.6694 - val_loss: 3.6017 - val_output_1_loss: 3.8004 - val_output_2_loss: 1.8132 - val_output_1_root_mean_squared_error: 1.9495 - val_output_2_root_mean_squared_error: 1.3466 162/162 [==============================] - 0s 781us/step - loss: 0.3652 - output_1_loss: 0.3570 - output_2_loss: 0.4387 - output_1_root_mean_squared_error: 0.5975 - output_2_root_mean_squared_error: 0.6624 WARNING:tensorflow:6 out of the last 7 calls to <function Model.make_predict_function.<locals>.predict_function at 0x7fb250b9d820> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details.
Saving and Restoring a Model¶
# extra code – delete the directory, in case it already exists
import shutil
shutil.rmtree("my_keras_model", ignore_errors=True)
model.save("my_keras_model", save_format="tf")
INFO:tensorflow:Assets written to: my_keras_model/assets
# extra code – show the contents of the my_keras_model/ directory
for path in sorted(Path("my_keras_model").glob("**/*")):
print(path)
my_keras_model/assets my_keras_model/keras_metadata.pb my_keras_model/saved_model.pb my_keras_model/variables my_keras_model/variables/variables.data-00000-of-00001 my_keras_model/variables/variables.index
model = tf.keras.models.load_model("my_keras_model")
y_pred_main, y_pred_aux = model.predict((X_new_wide, X_new_deep))
model.save_weights("my_weights")
model.load_weights("my_weights")
<tensorflow.python.training.tracking.util.CheckpointLoadStatus at 0x7fb210482490>
# extra code – show the list of my_weights.* files
for path in sorted(Path().glob("my_weights.*")):
print(path)
my_weights.data-00000-of-00001 my_weights.index
Using Callbacks¶
shutil.rmtree("my_checkpoints", ignore_errors=True) # extra code
checkpoint_cb = tf.keras.callbacks.ModelCheckpoint("my_checkpoints",
save_weights_only=True)
history = model.fit(
(X_train_wide, X_train_deep), (y_train, y_train), epochs=10,
validation_data=((X_valid_wide, X_valid_deep), (y_valid, y_valid)),
callbacks=[checkpoint_cb])
Epoch 1/10 363/363 [==============================] - 1s 2ms/step - loss: 0.3775 - output_1_loss: 0.3706 - output_2_loss: 0.4402 - output_1_root_mean_squared_error: 0.6088 - output_2_root_mean_squared_error: 0.6635 - val_loss: 0.3369 - val_output_1_loss: 0.3234 - val_output_2_loss: 0.4587 - val_output_1_root_mean_squared_error: 0.5687 - val_output_2_root_mean_squared_error: 0.6773 Epoch 2/10 363/363 [==============================] - 1s 1ms/step - loss: 0.3556 - output_1_loss: 0.3480 - output_2_loss: 0.4242 - output_1_root_mean_squared_error: 0.5899 - output_2_root_mean_squared_error: 0.6513 - val_loss: 0.4940 - val_output_1_loss: 0.4650 - val_output_2_loss: 0.7551 - val_output_1_root_mean_squared_error: 0.6819 - val_output_2_root_mean_squared_error: 0.8689 Epoch 3/10 363/363 [==============================] - 1s 1ms/step - loss: 0.3612 - output_1_loss: 0.3547 - output_2_loss: 0.4198 - output_1_root_mean_squared_error: 0.5956 - output_2_root_mean_squared_error: 0.6480 - val_loss: 0.3443 - val_output_1_loss: 0.3355 - val_output_2_loss: 0.4241 - val_output_1_root_mean_squared_error: 0.5792 - val_output_2_root_mean_squared_error: 0.6512 Epoch 4/10 363/363 [==============================] - 1s 1ms/step - loss: 0.3493 - output_1_loss: 0.3425 - output_2_loss: 0.4110 - output_1_root_mean_squared_error: 0.5852 - output_2_root_mean_squared_error: 0.6411 - val_loss: 0.4676 - val_output_1_loss: 0.4635 - val_output_2_loss: 0.5046 - val_output_1_root_mean_squared_error: 0.6808 - val_output_2_root_mean_squared_error: 0.7104 Epoch 5/10 363/363 [==============================] - 1s 1ms/step - loss: 0.3525 - output_1_loss: 0.3465 - output_2_loss: 0.4069 - output_1_root_mean_squared_error: 0.5886 - output_2_root_mean_squared_error: 0.6379 - val_loss: 1.3020 - val_output_1_loss: 1.3842 - val_output_2_loss: 0.5623 - val_output_1_root_mean_squared_error: 1.1765 - val_output_2_root_mean_squared_error: 0.7499 Epoch 6/10 363/363 [==============================] - 1s 1ms/step - loss: 0.3512 - output_1_loss: 0.3453 - output_2_loss: 0.4039 - output_1_root_mean_squared_error: 0.5876 - output_2_root_mean_squared_error: 0.6356 - val_loss: 1.6719 - val_output_1_loss: 1.7502 - val_output_2_loss: 0.9670 - val_output_1_root_mean_squared_error: 1.3230 - val_output_2_root_mean_squared_error: 0.9833 Epoch 7/10 363/363 [==============================] - 1s 1ms/step - loss: 0.3533 - output_1_loss: 0.3477 - output_2_loss: 0.4038 - output_1_root_mean_squared_error: 0.5897 - output_2_root_mean_squared_error: 0.6355 - val_loss: 0.6855 - val_output_1_loss: 0.7149 - val_output_2_loss: 0.4210 - val_output_1_root_mean_squared_error: 0.8455 - val_output_2_root_mean_squared_error: 0.6488 Epoch 8/10 363/363 [==============================] - 1s 1ms/step - loss: 0.3409 - output_1_loss: 0.3348 - output_2_loss: 0.3965 - output_1_root_mean_squared_error: 0.5786 - output_2_root_mean_squared_error: 0.6297 - val_loss: 2.0126 - val_output_1_loss: 1.9280 - val_output_2_loss: 2.7742 - val_output_1_root_mean_squared_error: 1.3885 - val_output_2_root_mean_squared_error: 1.6656 Epoch 9/10 363/363 [==============================] - 1s 1ms/step - loss: 0.3441 - output_1_loss: 0.3375 - output_2_loss: 0.4028 - output_1_root_mean_squared_error: 0.5810 - output_2_root_mean_squared_error: 0.6347 - val_loss: 1.6894 - val_output_1_loss: 1.8009 - val_output_2_loss: 0.6859 - val_output_1_root_mean_squared_error: 1.3420 - val_output_2_root_mean_squared_error: 0.8282 Epoch 10/10 363/363 [==============================] - 1s 1ms/step - loss: 0.3517 - output_1_loss: 0.3468 - output_2_loss: 0.3962 - output_1_root_mean_squared_error: 0.5889 - output_2_root_mean_squared_error: 0.6294 - val_loss: 1.2969 - val_output_1_loss: 1.3365 - val_output_2_loss: 0.9407 - val_output_1_root_mean_squared_error: 1.1561 - val_output_2_root_mean_squared_error: 0.9699
early_stopping_cb = tf.keras.callbacks.EarlyStopping(patience=10,
restore_best_weights=True)
history = model.fit(
(X_train_wide, X_train_deep), (y_train, y_train), epochs=100,
validation_data=((X_valid_wide, X_valid_deep), (y_valid, y_valid)),
callbacks=[checkpoint_cb, early_stopping_cb])
Epoch 1/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3405 - output_1_loss: 0.3349 - output_2_loss: 0.3910 - output_1_root_mean_squared_error: 0.5787 - output_2_root_mean_squared_error: 0.6253 - val_loss: 0.6245 - val_output_1_loss: 0.6502 - val_output_2_loss: 0.3937 - val_output_1_root_mean_squared_error: 0.8063 - val_output_2_root_mean_squared_error: 0.6275 Epoch 2/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3400 - output_1_loss: 0.3344 - output_2_loss: 0.3900 - output_1_root_mean_squared_error: 0.5783 - output_2_root_mean_squared_error: 0.6245 - val_loss: 0.9552 - val_output_1_loss: 0.9508 - val_output_2_loss: 0.9947 - val_output_1_root_mean_squared_error: 0.9751 - val_output_2_root_mean_squared_error: 0.9974 Epoch 3/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3442 - output_1_loss: 0.3389 - output_2_loss: 0.3921 - output_1_root_mean_squared_error: 0.5821 - output_2_root_mean_squared_error: 0.6262 - val_loss: 0.3574 - val_output_1_loss: 0.3552 - val_output_2_loss: 0.3766 - val_output_1_root_mean_squared_error: 0.5960 - val_output_2_root_mean_squared_error: 0.6137 Epoch 4/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3347 - output_1_loss: 0.3289 - output_2_loss: 0.3865 - output_1_root_mean_squared_error: 0.5735 - output_2_root_mean_squared_error: 0.6217 - val_loss: 0.4521 - val_output_1_loss: 0.4401 - val_output_2_loss: 0.5609 - val_output_1_root_mean_squared_error: 0.6634 - val_output_2_root_mean_squared_error: 0.7489 Epoch 5/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3363 - output_1_loss: 0.3311 - output_2_loss: 0.3832 - output_1_root_mean_squared_error: 0.5754 - output_2_root_mean_squared_error: 0.6190 - val_loss: 0.4903 - val_output_1_loss: 0.5018 - val_output_2_loss: 0.3869 - val_output_1_root_mean_squared_error: 0.7084 - val_output_2_root_mean_squared_error: 0.6220 Epoch 6/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3300 - output_1_loss: 0.3245 - output_2_loss: 0.3801 - output_1_root_mean_squared_error: 0.5696 - output_2_root_mean_squared_error: 0.6165 - val_loss: 0.8351 - val_output_1_loss: 0.8434 - val_output_2_loss: 0.7602 - val_output_1_root_mean_squared_error: 0.9184 - val_output_2_root_mean_squared_error: 0.8719 Epoch 7/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3324 - output_1_loss: 0.3270 - output_2_loss: 0.3814 - output_1_root_mean_squared_error: 0.5718 - output_2_root_mean_squared_error: 0.6176 - val_loss: 0.6880 - val_output_1_loss: 0.7171 - val_output_2_loss: 0.4259 - val_output_1_root_mean_squared_error: 0.8468 - val_output_2_root_mean_squared_error: 0.6526 Epoch 8/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3286 - output_1_loss: 0.3231 - output_2_loss: 0.3774 - output_1_root_mean_squared_error: 0.5684 - output_2_root_mean_squared_error: 0.6143 - val_loss: 4.4284 - val_output_1_loss: 4.2604 - val_output_2_loss: 5.9404 - val_output_1_root_mean_squared_error: 2.0641 - val_output_2_root_mean_squared_error: 2.4373 Epoch 9/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3378 - output_1_loss: 0.3322 - output_2_loss: 0.3886 - output_1_root_mean_squared_error: 0.5764 - output_2_root_mean_squared_error: 0.6234 - val_loss: 1.7043 - val_output_1_loss: 1.7984 - val_output_2_loss: 0.8578 - val_output_1_root_mean_squared_error: 1.3410 - val_output_2_root_mean_squared_error: 0.9262 Epoch 10/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3401 - output_1_loss: 0.3354 - output_2_loss: 0.3824 - output_1_root_mean_squared_error: 0.5792 - output_2_root_mean_squared_error: 0.6184 - val_loss: 0.6170 - val_output_1_loss: 0.6282 - val_output_2_loss: 0.5169 - val_output_1_root_mean_squared_error: 0.7926 - val_output_2_root_mean_squared_error: 0.7190 Epoch 11/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3230 - output_1_loss: 0.3177 - output_2_loss: 0.3706 - output_1_root_mean_squared_error: 0.5637 - output_2_root_mean_squared_error: 0.6088 - val_loss: 0.3558 - val_output_1_loss: 0.3490 - val_output_2_loss: 0.4170 - val_output_1_root_mean_squared_error: 0.5907 - val_output_2_root_mean_squared_error: 0.6457 Epoch 12/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3253 - output_1_loss: 0.3201 - output_2_loss: 0.3727 - output_1_root_mean_squared_error: 0.5658 - output_2_root_mean_squared_error: 0.6105 - val_loss: 0.4612 - val_output_1_loss: 0.4597 - val_output_2_loss: 0.4745 - val_output_1_root_mean_squared_error: 0.6780 - val_output_2_root_mean_squared_error: 0.6888 Epoch 13/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3221 - output_1_loss: 0.3167 - output_2_loss: 0.3699 - output_1_root_mean_squared_error: 0.5628 - output_2_root_mean_squared_error: 0.6082 - val_loss: 0.3120 - val_output_1_loss: 0.3056 - val_output_2_loss: 0.3694 - val_output_1_root_mean_squared_error: 0.5528 - val_output_2_root_mean_squared_error: 0.6078 Epoch 14/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3204 - output_1_loss: 0.3149 - output_2_loss: 0.3695 - output_1_root_mean_squared_error: 0.5612 - output_2_root_mean_squared_error: 0.6078 - val_loss: 0.4120 - val_output_1_loss: 0.4013 - val_output_2_loss: 0.5076 - val_output_1_root_mean_squared_error: 0.6335 - val_output_2_root_mean_squared_error: 0.7124 Epoch 15/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3196 - output_1_loss: 0.3144 - output_2_loss: 0.3662 - output_1_root_mean_squared_error: 0.5607 - output_2_root_mean_squared_error: 0.6052 - val_loss: 0.3304 - val_output_1_loss: 0.3269 - val_output_2_loss: 0.3619 - val_output_1_root_mean_squared_error: 0.5718 - val_output_2_root_mean_squared_error: 0.6016 Epoch 16/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3166 - output_1_loss: 0.3113 - output_2_loss: 0.3639 - output_1_root_mean_squared_error: 0.5579 - output_2_root_mean_squared_error: 0.6032 - val_loss: 0.4455 - val_output_1_loss: 0.4414 - val_output_2_loss: 0.4819 - val_output_1_root_mean_squared_error: 0.6644 - val_output_2_root_mean_squared_error: 0.6942 Epoch 17/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3186 - output_1_loss: 0.3134 - output_2_loss: 0.3650 - output_1_root_mean_squared_error: 0.5599 - output_2_root_mean_squared_error: 0.6041 - val_loss: 0.3255 - val_output_1_loss: 0.3212 - val_output_2_loss: 0.3643 - val_output_1_root_mean_squared_error: 0.5667 - val_output_2_root_mean_squared_error: 0.6035 Epoch 18/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3143 - output_1_loss: 0.3091 - output_2_loss: 0.3611 - output_1_root_mean_squared_error: 0.5560 - output_2_root_mean_squared_error: 0.6009 - val_loss: 1.6360 - val_output_1_loss: 1.6925 - val_output_2_loss: 1.1276 - val_output_1_root_mean_squared_error: 1.3010 - val_output_2_root_mean_squared_error: 1.0619 Epoch 19/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3169 - output_1_loss: 0.3122 - output_2_loss: 0.3601 - output_1_root_mean_squared_error: 0.5587 - output_2_root_mean_squared_error: 0.6001 - val_loss: 1.2441 - val_output_1_loss: 1.3093 - val_output_2_loss: 0.6572 - val_output_1_root_mean_squared_error: 1.1442 - val_output_2_root_mean_squared_error: 0.8107 Epoch 20/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3245 - output_1_loss: 0.3201 - output_2_loss: 0.3641 - output_1_root_mean_squared_error: 0.5658 - output_2_root_mean_squared_error: 0.6034 - val_loss: 1.5466 - val_output_1_loss: 1.5582 - val_output_2_loss: 1.4424 - val_output_1_root_mean_squared_error: 1.2483 - val_output_2_root_mean_squared_error: 1.2010 Epoch 21/100 363/363 [==============================] - 0s 1ms/step - loss: 0.3202 - output_1_loss: 0.3153 - output_2_loss: 0.3640 - output_1_root_mean_squared_error: 0.5615 - output_2_root_mean_squared_error: 0.6033 - val_loss: 0.6704 - val_output_1_loss: 0.6907 - val_output_2_loss: 0.4873 - val_output_1_root_mean_squared_error: 0.8311 - val_output_2_root_mean_squared_error: 0.6980 Epoch 22/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3150 - output_1_loss: 0.3103 - output_2_loss: 0.3573 - output_1_root_mean_squared_error: 0.5570 - output_2_root_mean_squared_error: 0.5978 - val_loss: 0.4909 - val_output_1_loss: 0.4955 - val_output_2_loss: 0.4493 - val_output_1_root_mean_squared_error: 0.7039 - val_output_2_root_mean_squared_error: 0.6703 Epoch 23/100 363/363 [==============================] - 1s 1ms/step - loss: 0.3104 - output_1_loss: 0.3054 - output_2_loss: 0.3552 - output_1_root_mean_squared_error: 0.5526 - output_2_root_mean_squared_error: 0.5960 - val_loss: 0.3845 - val_output_1_loss: 0.3803 - val_output_2_loss: 0.4228 - val_output_1_root_mean_squared_error: 0.6167 - val_output_2_root_mean_squared_error: 0.6502
class PrintValTrainRatioCallback(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
ratio = logs["val_loss"] / logs["loss"]
print(f"Epoch={epoch}, val/train={ratio:.2f}")
val_train_ratio_cb = PrintValTrainRatioCallback()
history = model.fit(
(X_train_wide, X_train_deep), (y_train, y_train), epochs=10,
validation_data=((X_valid_wide, X_valid_deep), (y_valid, y_valid)),
callbacks=[val_train_ratio_cb], verbose=0)
Epoch=0, val/train=2.29 Epoch=1, val/train=1.03 Epoch=2, val/train=2.07 Epoch=3, val/train=1.76 Epoch=4, val/train=3.56 Epoch=5, val/train=1.86 Epoch=6, val/train=2.45 Epoch=7, val/train=7.86 Epoch=8, val/train=11.20 Epoch=9, val/train=1.14
Using TensorBoard for Visualization¶
TensorBoard is preinstalled on Colab, but not the tensorboard-plugin-profile, so let's install it:
if "google.colab" in sys.modules: # extra code
%pip install -q -U tensorboard-plugin-profile
shutil.rmtree("my_logs", ignore_errors=True)
from pathlib import Path
from time import strftime
def get_run_logdir(root_logdir="my_logs"):
return Path(root_logdir) / strftime("run_%Y_%m_%d_%H_%M_%S")
run_logdir = get_run_logdir()
# extra code – builds the first regression model we used earlier
tf.keras.backend.clear_session()
tf.random.set_seed(42)
norm_layer = tf.keras.layers.Normalization(input_shape=X_train.shape[1:])
model = tf.keras.Sequential([
norm_layer,
tf.keras.layers.Dense(30, activation="relu"),
tf.keras.layers.Dense(30, activation="relu"),
tf.keras.layers.Dense(1)
])
optimizer = tf.keras.optimizers.SGD(learning_rate=1e-3)
model.compile(loss="mse", optimizer=optimizer, metrics=["RootMeanSquaredError"])
norm_layer.adapt(X_train)
tensorboard_cb = tf.keras.callbacks.TensorBoard(run_logdir,
profile_batch=(100, 200))
history = model.fit(X_train, y_train, epochs=20,
validation_data=(X_valid, y_valid),
callbacks=[tensorboard_cb])
2022-08-01 17:25:59.099970: I tensorflow/core/profiler/lib/profiler_session.cc:110] Profiler session initializing. 2022-08-01 17:25:59.099982: I tensorflow/core/profiler/lib/profiler_session.cc:125] Profiler session started. 2022-08-01 17:25:59.100137: I tensorflow/core/profiler/lib/profiler_session.cc:143] Profiler session tear down.
Epoch 1/20 261/363 [====================>.........] - ETA: 0s - loss: 2.3165 - root_mean_squared_error: 1.5220
2022-08-01 17:25:59.430946: I tensorflow/core/profiler/lib/profiler_session.cc:110] Profiler session initializing. 2022-08-01 17:25:59.430962: I tensorflow/core/profiler/lib/profiler_session.cc:125] Profiler session started. 2022-08-01 17:25:59.510100: I tensorflow/core/profiler/lib/profiler_session.cc:67] Profiler session collecting data. 2022-08-01 17:25:59.524969: I tensorflow/core/profiler/lib/profiler_session.cc:143] Profiler session tear down. 2022-08-01 17:25:59.539451: I tensorflow/core/profiler/rpc/client/save_profile.cc:136] Creating directory: my_logs/run_2022_08_01_17_25_59/plugins/profile/2022_08_01_17_26_00 2022-08-01 17:25:59.549606: I tensorflow/core/profiler/rpc/client/save_profile.cc:142] Dumped gzipped tool data for trace.json.gz to my_logs/run_2022_08_01_17_25_59/plugins/profile/2022_08_01_17_26_00/my_computer.trace.json.gz 2022-08-01 17:25:59.558338: I tensorflow/core/profiler/rpc/client/save_profile.cc:136] Creating directory: my_logs/run_2022_08_01_17_25_59/plugins/profile/2022_08_01_17_26_00 2022-08-01 17:25:59.558474: I tensorflow/core/profiler/rpc/client/save_profile.cc:142] Dumped gzipped tool data for memory_profile.json.gz to my_logs/run_2022_08_01_17_25_59/plugins/profile/2022_08_01_17_26_00/my_computer.memory_profile.json.gz 2022-08-01 17:25:59.559618: I tensorflow/core/profiler/rpc/client/capture_profile.cc:251] Creating directory: my_logs/run_2022_08_01_17_25_59/plugins/profile/2022_08_01_17_26_00 Dumped tool data for xplane.pb to my_logs/run_2022_08_01_17_25_59/plugins/profile/2022_08_01_17_26_00/my_computer.xplane.pb Dumped tool data for overview_page.pb to my_logs/run_2022_08_01_17_25_59/plugins/profile/2022_08_01_17_26_00/my_computer.overview_page.pb Dumped tool data for input_pipeline.pb to my_logs/run_2022_08_01_17_25_59/plugins/profile/2022_08_01_17_26_00/my_computer.input_pipeline.pb Dumped tool data for tensorflow_stats.pb to my_logs/run_2022_08_01_17_25_59/plugins/profile/2022_08_01_17_26_00/my_computer.tensorflow_stats.pb Dumped tool data for kernel_stats.pb to my_logs/run_2022_08_01_17_25_59/plugins/profile/2022_08_01_17_26_00/my_computer.kernel_stats.pb
363/363 [==============================] - 1s 1ms/step - loss: 1.8866 - root_mean_squared_error: 1.3736 - val_loss: 0.7126 - val_root_mean_squared_error: 0.8442 Epoch 2/20 363/363 [==============================] - 0s 907us/step - loss: 0.6577 - root_mean_squared_error: 0.8110 - val_loss: 0.6880 - val_root_mean_squared_error: 0.8295 Epoch 3/20 363/363 [==============================] - 0s 836us/step - loss: 0.5934 - root_mean_squared_error: 0.7703 - val_loss: 0.5803 - val_root_mean_squared_error: 0.7618 Epoch 4/20 363/363 [==============================] - 0s 832us/step - loss: 0.5557 - root_mean_squared_error: 0.7455 - val_loss: 0.5166 - val_root_mean_squared_error: 0.7188 Epoch 5/20 363/363 [==============================] - 0s 985us/step - loss: 0.5272 - root_mean_squared_error: 0.7261 - val_loss: 0.4895 - val_root_mean_squared_error: 0.6997 Epoch 6/20 363/363 [==============================] - 0s 887us/step - loss: 0.5033 - root_mean_squared_error: 0.7094 - val_loss: 0.4951 - val_root_mean_squared_error: 0.7036 Epoch 7/20 363/363 [==============================] - 0s 894us/step - loss: 0.4854 - root_mean_squared_error: 0.6967 - val_loss: 0.4862 - val_root_mean_squared_error: 0.6973 Epoch 8/20 363/363 [==============================] - 0s 868us/step - loss: 0.4709 - root_mean_squared_error: 0.6862 - val_loss: 0.4554 - val_root_mean_squared_error: 0.6748 Epoch 9/20 363/363 [==============================] - 0s 780us/step - loss: 0.4578 - root_mean_squared_error: 0.6766 - val_loss: 0.4413 - val_root_mean_squared_error: 0.6643 Epoch 10/20 363/363 [==============================] - 0s 819us/step - loss: 0.4474 - root_mean_squared_error: 0.6689 - val_loss: 0.4379 - val_root_mean_squared_error: 0.6617 Epoch 11/20 363/363 [==============================] - 0s 795us/step - loss: 0.4393 - root_mean_squared_error: 0.6628 - val_loss: 0.4396 - val_root_mean_squared_error: 0.6630 Epoch 12/20 363/363 [==============================] - 0s 852us/step - loss: 0.4318 - root_mean_squared_error: 0.6571 - val_loss: 0.4505 - val_root_mean_squared_error: 0.6712 Epoch 13/20 363/363 [==============================] - 0s 910us/step - loss: 0.4260 - root_mean_squared_error: 0.6527 - val_loss: 0.3997 - val_root_mean_squared_error: 0.6322 Epoch 14/20 363/363 [==============================] - 0s 796us/step - loss: 0.4202 - root_mean_squared_error: 0.6482 - val_loss: 0.3956 - val_root_mean_squared_error: 0.6290 Epoch 15/20 363/363 [==============================] - 0s 816us/step - loss: 0.4155 - root_mean_squared_error: 0.6446 - val_loss: 0.3916 - val_root_mean_squared_error: 0.6257 Epoch 16/20 363/363 [==============================] - 0s 759us/step - loss: 0.4112 - root_mean_squared_error: 0.6412 - val_loss: 0.3937 - val_root_mean_squared_error: 0.6275 Epoch 17/20 363/363 [==============================] - 0s 826us/step - loss: 0.4077 - root_mean_squared_error: 0.6385 - val_loss: 0.3809 - val_root_mean_squared_error: 0.6172 Epoch 18/20 363/363 [==============================] - 0s 832us/step - loss: 0.4039 - root_mean_squared_error: 0.6356 - val_loss: 0.3793 - val_root_mean_squared_error: 0.6159 Epoch 19/20 363/363 [==============================] - 0s 747us/step - loss: 0.4004 - root_mean_squared_error: 0.6328 - val_loss: 0.3850 - val_root_mean_squared_error: 0.6205 Epoch 20/20 363/363 [==============================] - 0s 755us/step - loss: 0.3980 - root_mean_squared_error: 0.6308 - val_loss: 0.3809 - val_root_mean_squared_error: 0.6172
print("my_logs")
for path in sorted(Path("my_logs").glob("**/*")):
print(" " * (len(path.parts) - 1) + path.parts[-1])
my_logs
run_2022_08_01_17_25_59
events.out.tfevents.1638910166.my_computer.profile-empty
plugins
profile
2022_08_01_17_26_00
my_computer.input_pipeline.pb
my_computer.kernel_stats.pb
my_computer.memory_profile.json.gz
my_computer.overview_page.pb
my_computer.tensorflow_stats.pb
my_computer.trace.json.gz
my_computer.xplane.pb
train
events.out.tfevents.1638910166.my_computer.22294.0.v2
validation
events.out.tfevents.1638910166.my_computer.22294.1.v2
Let's load the tensorboard Jupyter extension and start the TensorBoard server:
%load_ext tensorboard
%tensorboard --logdir=./my_logs
Note: if you prefer to access TensorBoard in a separate tab, click the "localhost:6006" link below:
# extra code
if "google.colab" in sys.modules:
from google.colab import output
output.serve_kernel_port_as_window(6006)
else:
from IPython.display import display, HTML
display(HTML('<a href="http://localhost:6006/">http://localhost:6006/</a>'))
You can use also visualize histograms, images, text, and even listen to audio using TensorBoard:
test_logdir = get_run_logdir()
writer = tf.summary.create_file_writer(str(test_logdir))
with writer.as_default():
for step in range(1, 1000 + 1):
tf.summary.scalar("my_scalar", np.sin(step / 10), step=step)
data = (np.random.randn(100) + 2) * step / 100 # gets larger
tf.summary.histogram("my_hist", data, buckets=50, step=step)
images = np.random.rand(2, 32, 32, 3) * step / 1000 # gets brighter
tf.summary.image("my_images", images, step=step)
texts = ["The step is " + str(step), "Its square is " + str(step ** 2)]
tf.summary.text("my_text", texts, step=step)
sine_wave = tf.math.sin(tf.range(12000) / 48000 * 2 * np.pi * step)
audio = tf.reshape(tf.cast(sine_wave, tf.float32), [1, -1, 1])
tf.summary.audio("my_audio", audio, sample_rate=48000, step=step)
Note: it used to be possible to easily share your TensorBoard logs with the world by uploading them to https://tensorboard.dev/. Sadly, this service will shut down in December 2023, so I have removed the corresponding code examples from this notebook.
When you stop this Jupyter kernel (a.k.a. Runtime), it will automatically stop the TensorBoard server as well. Another way to stop the TensorBoard server is to kill it, if you are running on Linux or MacOSX. First, you need to find its process ID:
# extra code – lists all running TensorBoard server instances
from tensorboard import notebook
notebook.list()
Known TensorBoard instances: - port 6006: logdir ./my_logs (started 0:00:31 ago; pid 22701)
Next you can use the following command on Linux or MacOSX, replacing <pid> with the pid listed above:
!kill <pid>
On Windows:
!taskkill /F /PID <pid>
Fine-Tuning Neural Network Hyperparameters¶
In this section we'll use the Fashion MNIST dataset again:
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist
X_train, y_train = X_train_full[:-5000], y_train_full[:-5000]
X_valid, y_valid = X_train_full[-5000:], y_train_full[-5000:]
tf.keras.backend.clear_session()
tf.random.set_seed(42)
if "google.colab" in sys.modules:
%pip install -q -U keras_tuner
import keras_tuner as kt
def build_model(hp):
n_hidden = hp.Int("n_hidden", min_value=0, max_value=8, default=2)
n_neurons = hp.Int("n_neurons", min_value=16, max_value=256)
learning_rate = hp.Float("learning_rate", min_value=1e-4, max_value=1e-2,
sampling="log")
optimizer = hp.Choice("optimizer", values=["sgd", "adam"])
if optimizer == "sgd":
optimizer = tf.keras.optimizers.SGD(learning_rate=learning_rate)
else:
optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate)
model = tf.keras.Sequential()
model.add(tf.keras.layers.Flatten())
for _ in range(n_hidden):
model.add(tf.keras.layers.Dense(n_neurons, activation="relu"))
model.add(tf.keras.layers.Dense(10, activation="softmax"))
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
return model
random_search_tuner = kt.RandomSearch(
build_model, objective="val_accuracy", max_trials=5, overwrite=True,
directory="my_fashion_mnist", project_name="my_rnd_search", seed=42)
random_search_tuner.search(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
Trial 5 Complete [00h 00m 24s] val_accuracy: 0.8736000061035156 Best val_accuracy So Far: 0.8736000061035156 Total elapsed time: 00h 01m 43s INFO:tensorflow:Oracle triggered exit
I1208 09:51:50.359315 4451454400 1158129808.py:4] Oracle triggered exit
top3_models = random_search_tuner.get_best_models(num_models=3)
best_model = top3_models[0]
top3_params = random_search_tuner.get_best_hyperparameters(num_trials=3)
top3_params[0].values # best hyperparameter values
{'n_hidden': 5,
'n_neurons': 70,
'learning_rate': 0.00041268008323824807,
'optimizer': 'adam'}
best_trial = random_search_tuner.oracle.get_best_trials(num_trials=1)[0]
best_trial.summary()
Trial summary Hyperparameters: n_hidden: 5 n_neurons: 70 learning_rate: 0.00041268008323824807 optimizer: adam Score: 0.8736000061035156
best_trial.metrics.get_last_value("val_accuracy")
0.8736000061035156
best_model.fit(X_train_full, y_train_full, epochs=10)
test_loss, test_accuracy = best_model.evaluate(X_test, y_test)
Epoch 1/10 1875/1875 [==============================] - 3s 1ms/step - loss: 0.3274 - accuracy: 0.8799 Epoch 2/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.3155 - accuracy: 0.8827 Epoch 3/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.3049 - accuracy: 0.8867 Epoch 4/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.2962 - accuracy: 0.8914 Epoch 5/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.2886 - accuracy: 0.8931 Epoch 6/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.2831 - accuracy: 0.8935 Epoch 7/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.2795 - accuracy: 0.8962 Epoch 8/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.2701 - accuracy: 0.8999: 0s - loss: 0 Epoch 9/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.2661 - accuracy: 0.9009 Epoch 10/10 1875/1875 [==============================] - 2s 1ms/step - loss: 0.2628 - accuracy: 0.9012 313/313 [==============================] - 0s 744us/step - loss: 0.3625 - accuracy: 0.8753
class MyClassificationHyperModel(kt.HyperModel):
def build(self, hp):
return build_model(hp)
def fit(self, hp, model, X, y, **kwargs):
if hp.Boolean("normalize"):
norm_layer = tf.keras.layers.Normalization()
X = norm_layer(X)
return model.fit(X, y, **kwargs)
hyperband_tuner = kt.Hyperband(
MyClassificationHyperModel(), objective="val_accuracy", seed=42,
max_epochs=10, factor=3, hyperband_iterations=2,
overwrite=True, directory="my_fashion_mnist", project_name="hyperband")
root_logdir = Path(hyperband_tuner.project_dir) / "tensorboard"
tensorboard_cb = tf.keras.callbacks.TensorBoard(root_logdir)
early_stopping_cb = tf.keras.callbacks.EarlyStopping(patience=2)
hyperband_tuner.search(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid),
callbacks=[early_stopping_cb, tensorboard_cb])
Trial 60 Complete [00h 00m 18s] val_accuracy: 0.819599986076355 Best val_accuracy So Far: 0.8704000115394592 Total elapsed time: 00h 08m 44s INFO:tensorflow:Oracle triggered exit
I1208 10:00:59.856360 4451454400 3169670597.py:4] Oracle triggered exit
bayesian_opt_tuner = kt.BayesianOptimization(
MyClassificationHyperModel(), objective="val_accuracy", seed=42,
max_trials=10, alpha=1e-4, beta=2.6,
overwrite=True, directory="my_fashion_mnist", project_name="bayesian_opt")
bayesian_opt_tuner.search(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid),
callbacks=[early_stopping_cb])
Trial 10 Complete [00h 00m 13s] val_accuracy: 0.7228000164031982 Best val_accuracy So Far: 0.8636000156402588 Total elapsed time: 00h 02m 10s INFO:tensorflow:Oracle triggered exit
I1208 10:03:10.004801 4451454400 1918178380.py:5] Oracle triggered exit
%tensorboard --logdir {root_logdir}
Exercise solutions¶
1. to 9.¶
- Visit the TensorFlow Playground and play around with it, as described in this exercise.
- Here is a neural network based on the original artificial neurons that computes A ⊕ B (where ⊕ represents the exclusive OR), using the fact that A ⊕ B = (A ∧ ¬ B) ∨ (¬ A ∧ B). There are other solutions—for example, using the fact that A ⊕ B = (A ∨ B) ∧ ¬(A ∧ B), or the fact that A ⊕ B = (A ∨ B) ∧ (¬ A ∨ ¬ B), and so on.
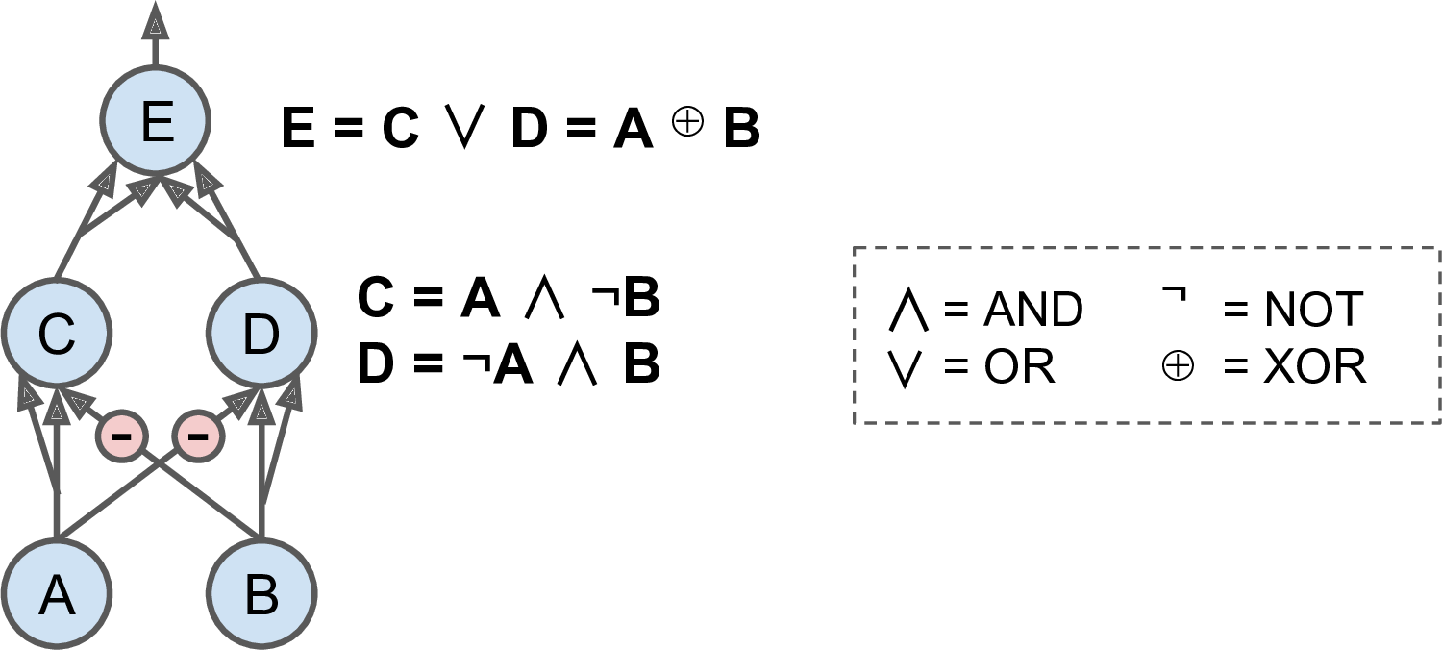
- A classical Perceptron will converge only if the dataset is linearly separable, and it won't be able to estimate class probabilities. In contrast, a Logistic Regression classifier will generally converge to a reasonably good solution even if the dataset is not linearly separable, and it will output class probabilities. If you change the Perceptron's activation function to the sigmoid activation function (or the softmax activation function if there are multiple neurons), and if you train it using Gradient Descent (or some other optimization algorithm minimizing the cost function, typically cross entropy), then it becomes equivalent to a Logistic Regression classifier.
- The sigmoid activation function was a key ingredient in training the first MLPs because its derivative is always nonzero, so Gradient Descent can always roll down the slope. When the activation function is a step function, Gradient Descent cannot move, as there is no slope at all.
- Popular activation functions include the step function, the sigmoid function, the hyperbolic tangent (tanh) function, and the Rectified Linear Unit (ReLU) function (see Figure 10-8). See Chapter 11 for other examples, such as ELU and variants of the ReLU function.
- Considering the MLP described in the question, composed of one input layer with 10 passthrough neurons, followed by one hidden layer with 50 artificial neurons, and finally one output layer with 3 artificial neurons, where all artificial neurons use the ReLU activation function:
- The shape of the input matrix X is m × 10, where m represents the training batch size.
- The shape of the hidden layer's weight matrix Wh is 10 × 50, and the length of its bias vector bh is 50.
- The shape of the output layer's weight matrix Wo is 50 × 3, and the length of its bias vector bo is 3.
- The shape of the network's output matrix Y is m × 3.
- Y = ReLU(ReLU(X Wh + bh) Wo + bo). Recall that the ReLU function just sets every negative number in the matrix to zero. Also note that when you are adding a bias vector to a matrix, it is added to every single row in the matrix, which is called broadcasting.
- To classify email into spam or ham, you just need one neuron in the output layer of a neural network—for example, indicating the probability that the email is spam. You would typically use the sigmoid activation function in the output layer when estimating a probability. If instead you want to tackle MNIST, you need 10 neurons in the output layer, and you must replace the sigmoid function with the softmax activation function, which can handle multiple classes, outputting one probability per class. If you want your neural network to predict housing prices like in Chapter 2, then you need one output neuron, using no activation function at all in the output layer. Note: when the values to predict can vary by many orders of magnitude, you may want to predict the logarithm of the target value rather than the target value directly. Simply computing the exponential of the neural network's output will give you the estimated value (since exp(log v) = v).
- Backpropagation is a technique used to train artificial neural networks. It first computes the gradients of the cost function with regard to every model parameter (all the weights and biases), then it performs a Gradient Descent step using these gradients. This backpropagation step is typically performed thousands or millions of times, using many training batches, until the model parameters converge to values that (hopefully) minimize the cost function. To compute the gradients, backpropagation uses reverse-mode autodiff (although it wasn't called that when backpropagation was invented, and it has been reinvented several times). Reverse-mode autodiff performs a forward pass through a computation graph, computing every node's value for the current training batch, and then it performs a reverse pass, computing all the gradients at once (see Appendix B for more details). So what's the difference? Well, backpropagation refers to the whole process of training an artificial neural network using multiple backpropagation steps, each of which computes gradients and uses them to perform a Gradient Descent step. In contrast, reverse-mode autodiff is just a technique to compute gradients efficiently, and it happens to be used by backpropagation.
- Here is a list of all the hyperparameters you can tweak in a basic MLP: the number of hidden layers, the number of neurons in each hidden layer, and the activation function used in each hidden layer and in the output layer. In general, the ReLU activation function (or one of its variants; see Chapter 11) is a good default for the hidden layers. For the output layer, in general you will want the sigmoid activation function for binary classification, the softmax activation function for multiclass classification, or no activation function for regression. If the MLP overfits the training data, you can try reducing the number of hidden layers and reducing the number of neurons per hidden layer.
10.¶
Exercise: Train a deep MLP on the MNIST dataset (you can load it using tf.keras.datasets.mnist.load_data(). See if you can get over 98% accuracy by manually tuning the hyperparameters. Try searching for the optimal learning rate by using the approach presented in this chapter (i.e., by growing the learning rate exponentially, plotting the loss, and finding the point where the loss shoots up). Next, try tuning the hyperparameters using Keras Tuner with all the bells and whistles—save checkpoints, use early stopping, and plot learning curves using TensorBoard.
TODO: update this solution to use Keras Tuner.
Let's load the dataset:
(X_train_full, y_train_full), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
Just like for the Fashion MNIST dataset, the MNIST training set contains 60,000 grayscale images, each 28x28 pixels:
X_train_full.shape
(60000, 28, 28)
Each pixel intensity is also represented as a byte (0 to 255):
X_train_full.dtype
dtype('uint8')
Let's split the full training set into a validation set and a (smaller) training set. We also scale the pixel intensities down to the 0-1 range and convert them to floats, by dividing by 255, just like we did for Fashion MNIST:
X_valid, X_train = X_train_full[:5000] / 255., X_train_full[5000:] / 255.
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
X_test = X_test / 255.
Let's plot an image using Matplotlib's imshow() function, with a 'binary'
color map:
plt.imshow(X_train[0], cmap="binary")
plt.axis('off')
plt.show()
The labels are the class IDs (represented as uint8), from 0 to 9. Conveniently, the class IDs correspond to the digits represented in the images, so we don't need a class_names array:
y_train
array([7, 3, 4, ..., 5, 6, 8], dtype=uint8)
The validation set contains 5,000 images, and the test set contains 10,000 images:
X_valid.shape
(5000, 28, 28)
X_test.shape
(10000, 28, 28)
Let's take a look at a sample of the images in the dataset:
n_rows = 4
n_cols = 10
plt.figure(figsize=(n_cols * 1.2, n_rows * 1.2))
for row in range(n_rows):
for col in range(n_cols):
index = n_cols * row + col
plt.subplot(n_rows, n_cols, index + 1)
plt.imshow(X_train[index], cmap="binary", interpolation="nearest")
plt.axis('off')
plt.title(y_train[index])
plt.subplots_adjust(wspace=0.2, hspace=0.5)
plt.show()
Let's build a simple dense network and find the optimal learning rate. We will need a callback to grow the learning rate at each iteration. It will also record the learning rate and the loss at each iteration:
K = tf.keras.backend
class ExponentialLearningRate(tf.keras.callbacks.Callback):
def __init__(self, factor):
self.factor = factor
self.rates = []
self.losses = []
def on_batch_end(self, batch, logs):
self.rates.append(K.get_value(self.model.optimizer.learning_rate))
self.losses.append(logs["loss"])
K.set_value(self.model.optimizer.learning_rate, self.model.optimizer.learning_rate * self.factor)
tf.keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.Dense(300, activation="relu"),
tf.keras.layers.Dense(100, activation="relu"),
tf.keras.layers.Dense(10, activation="softmax")
])
We will start with a small learning rate of 1e-3, and grow it by 0.5% at each iteration:
optimizer = tf.keras.optimizers.SGD(learning_rate=1e-3)
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
expon_lr = ExponentialLearningRate(factor=1.005)
Now let's train the model for just 1 epoch:
history = model.fit(X_train, y_train, epochs=1,
validation_data=(X_valid, y_valid),
callbacks=[expon_lr])
1719/1719 [==============================] - 3s 2ms/step - loss: nan - accuracy: 0.5843 - val_loss: nan - val_accuracy: 0.0958
We can now plot the loss as a functionof the learning rate:
plt.plot(expon_lr.rates, expon_lr.losses)
plt.gca().set_xscale('log')
plt.hlines(min(expon_lr.losses), min(expon_lr.rates), max(expon_lr.rates))
plt.axis([min(expon_lr.rates), max(expon_lr.rates), 0, expon_lr.losses[0]])
plt.grid()
plt.xlabel("Learning rate")
plt.ylabel("Loss")
Text(0, 0.5, 'Loss')
The loss starts shooting back up violently when the learning rate goes over 6e-1, so let's try using half of that, at 3e-1:
tf.keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=[28, 28]),
tf.keras.layers.Dense(300, activation="relu"),
tf.keras.layers.Dense(100, activation="relu"),
tf.keras.layers.Dense(10, activation="softmax")
])
optimizer = tf.keras.optimizers.SGD(learning_rate=3e-1)
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
run_index = 1 # increment this at every run
run_logdir = Path() / "my_mnist_logs" / "run_{:03d}".format(run_index)
run_logdir
PosixPath('my_mnist_logs/run_001')
early_stopping_cb = tf.keras.callbacks.EarlyStopping(patience=20)
checkpoint_cb = tf.keras.callbacks.ModelCheckpoint("my_mnist_model", save_best_only=True)
tensorboard_cb = tf.keras.callbacks.TensorBoard(run_logdir)
history = model.fit(X_train, y_train, epochs=100,
validation_data=(X_valid, y_valid),
callbacks=[checkpoint_cb, early_stopping_cb, tensorboard_cb])
Epoch 1/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.2363 - accuracy: 0.9264 - val_loss: 0.0972 - val_accuracy: 0.9720 Epoch 2/100 1719/1719 [==============================] - 2s 997us/step - loss: 0.0948 - accuracy: 0.9702 - val_loss: 0.1035 - val_accuracy: 0.9706 Epoch 3/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0667 - accuracy: 0.9792 - val_loss: 0.0783 - val_accuracy: 0.9770 Epoch 4/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0463 - accuracy: 0.9848 - val_loss: 0.0827 - val_accuracy: 0.9766 Epoch 5/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0359 - accuracy: 0.9881 - val_loss: 0.0698 - val_accuracy: 0.9826 Epoch 6/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0297 - accuracy: 0.9908 - val_loss: 0.1048 - val_accuracy: 0.9758 Epoch 7/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0245 - accuracy: 0.9917 - val_loss: 0.0932 - val_accuracy: 0.9794 Epoch 8/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0239 - accuracy: 0.9922 - val_loss: 0.0816 - val_accuracy: 0.9798 Epoch 9/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0154 - accuracy: 0.9952 - val_loss: 0.0775 - val_accuracy: 0.9838 Epoch 10/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0126 - accuracy: 0.9960 - val_loss: 0.0805 - val_accuracy: 0.9812 Epoch 11/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0111 - accuracy: 0.9964 - val_loss: 0.0962 - val_accuracy: 0.9804 Epoch 12/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0118 - accuracy: 0.9963 - val_loss: 0.1044 - val_accuracy: 0.9774 Epoch 13/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0114 - accuracy: 0.9961 - val_loss: 0.1055 - val_accuracy: 0.9802 Epoch 14/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0150 - accuracy: 0.9948 - val_loss: 0.0993 - val_accuracy: 0.9826 Epoch 15/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0054 - accuracy: 0.9981 - val_loss: 0.0955 - val_accuracy: 0.9822 Epoch 16/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0046 - accuracy: 0.9984 - val_loss: 0.0982 - val_accuracy: 0.9822 Epoch 17/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0055 - accuracy: 0.9983 - val_loss: 0.0908 - val_accuracy: 0.9844 Epoch 18/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0070 - accuracy: 0.9978 - val_loss: 0.0883 - val_accuracy: 0.9840 Epoch 19/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0025 - accuracy: 0.9992 - val_loss: 0.0978 - val_accuracy: 0.9838 Epoch 20/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0058 - accuracy: 0.9983 - val_loss: 0.1011 - val_accuracy: 0.9830 Epoch 21/100 1719/1719 [==============================] - 2s 1ms/step - loss: 0.0039 - accuracy: 0.9989 - val_loss: 0.0991 - val_accuracy: 0.9840 Epoch 22/100 1719/1719 [==============================] - 2s 1ms/step - loss: 9.2480e-04 - accuracy: 0.9998 - val_loss: 0.0963 - val_accuracy: 0.9840 Epoch 23/100 1719/1719 [==============================] - 2s 1ms/step - loss: 1.2642e-04 - accuracy: 1.0000 - val_loss: 0.0970 - val_accuracy: 0.9846 Epoch 24/100 1719/1719 [==============================] - 2s 1ms/step - loss: 6.9068e-05 - accuracy: 1.0000 - val_loss: 0.0970 - val_accuracy: 0.9854 Epoch 25/100 1719/1719 [==============================] - 2s 1ms/step - loss: 5.1481e-05 - accuracy: 1.0000 - val_loss: 0.0977 - val_accuracy: 0.9850
model = tf.keras.models.load_model("my_mnist_model") # rollback to best model
model.evaluate(X_test, y_test)
313/313 [==============================] - 0s 908us/step - loss: 0.0708 - accuracy: 0.9799
[0.07079131156206131, 0.9799000024795532]
We got over 98% accuracy. Finally, let's look at the learning curves using TensorBoard:
%tensorboard --logdir=./my_mnist_logs
