Notebook

Basic Graph Theory. Methods of Graph Representation in Python.¶

Compiled by cyterat
_{* Most information in this notebook can be found on YouTube: David Amos: Graph Theory With Python}
_{* Visuals in the Graph Theory (basics) section were made by cyterat using draw.io}
_{* Gif in the (PyVis) FrankenGraph section was made by cyterat using screentogif}

Things worth looking into:

YouTube playlist David Amos: Graph Theory With Python
Book Intro to Graph Theory, Richard J. Trudeau
Brilliant's Graph Theory (Königsberg Bridge Problem is here as well)
PyVis library graphs examples https://visjs.github.io/vis-network/examples/
https://maelfabien.github.io/machinelearning/graph_1/#basic-graph-notions

Graph Theory (basics)¶

$G = (V, E)$

$G$ - graph
$V$ - vertex set (nodes)
$E$ - edge set (lines)

graph
In the graph above:
$V$ = { 0, 1, 2, 3 } - 4 vertices (nodes)
$E$ = { ( 0, 0 ), ( 0, 1 ), ( 0, 3 ), ( 1, 3 ), ( 1, 2 ), ( 2, 3 ) } - 6 edges (lines)
*loop counts as one edge

There are multiple ways of graphical representation of the vertex and edge sets from the previous graph. All variants below are correct, and represent the same graph.
graph

A multigraph can have several edges (lines), often called parallel, connecting the same vertices (nodes).

multigraph-graph
In a graph above:
$V$ = { 0, 1, 2, 3 } - 4 vertices (nodes)
$E$ = { ( 0, 1 ), ( 0, 1 ), ( 0, 3 ), ( 1, 2 ), ( 2, 3 ), ( 2, 3 ) } - 6 edges (lines)

Orientation¶

Graphs serve as a great tool to model relationships between objects. Such models can have a "direction" in their relationship, called orientation in a graph theory. This concept might be better understood by looking at social networks.

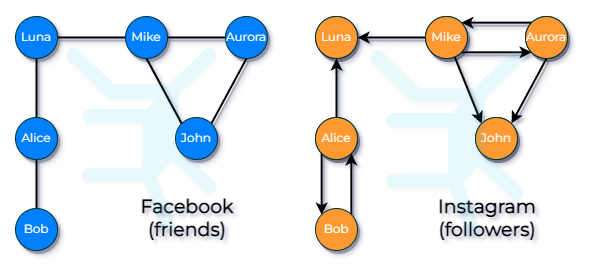
The examples above represent 2 types of graphs:

Undirected (Facebook) - edge represents relationship between nodes. (i.e. no arrows)
- Luna and Mike are friends, therefore if Luna has Mike in a her friendlist then Mike will automatically have Luna in his friendlist.
Directed (Instagram) - edge represents relationship between the node at the start of the edge and a node at the end of the edge. Not the other way around. (i.e. with arrows)
- Mike is a follower of a Luna, however Luna does not follow Mike.

Degree¶

The vertices (nodes) of a graph have a property called degree (valency), denoted as deg(v). It is basically a number of edges (lines) connected (incident) to a vertex (node).

The degree sequence of a graph is a list of all degrees of a graph, e.g. $(3,\ 3,\ 1,\ 1,\ 1,\ 1)$.
These degrees can be written in any order. In general however the degree sequence is written from max to min (non-increasing order).

A degree sequence with negative numbers cannot exist, since nodes cannot have negative degrees, e.g. $(-1,\ 2,\ 3,-3)$.
A degree sequence with 0 cannot exist, e.g. $(3,\ 2,\ 3,\ 0)$.

In most cases, a single degree sequence can represent multiple graphs, which may not look alike.

Can you tell if a sequence is graphic, i.e. if it can be represented using a graph?
Yes, here is a simple rule:

The Handshaking Lemma: The sum of the degrees of a graph is even.

$(3,\ 3,\ 3,\ 3,\ 3)$ --- is this a graph?

$3 \times 5 = 15$ , not an even number, so it is not a graphic sequence.

The Handshaking Lemma is not a theorem, there is not enough information taken into account to make a strong conclusion.
graphs-handshaking-fail
For example, let's look at a degree sequence $(2,\ 2)$ which represents the graph above:
$2 + 2 = 4$ , the result is an even number, however it is not graphical, beacuse it tries to show 2 connected nodes, with 1 edge each, not connected to anything.

Degree (Undirected Graph)¶

graphs-degree
_{*Note: the example was reduced to essentials, thats why some other nodes which should be connected to the ones displayed are excluded.}

In the example above:

vertex CP-0 has 3 edges, therefore $deg($CP-0$) = 3$
vertex CP-1 has 2 edges and a loop which contributes 2 to the vertex's degree, therefore $deg($CP-1$) = 4$

Some other concepts worth mentioning are:

Min Degree $\delta$ -- the smallest degree among all nodes in a graph;
Max Degree $\Delta$ -- the largest degree among all nodes in a graph;

Degree (Directed Graph)¶

The concept of orientation in this type of graphs introduces 2 new things: indegree and outdegree.

$deg^-(v)$ - indegree -- number of edge "heads" connected to a vertex (node);
$deg^+(v)$ - outdegree -- number of "tails" connected to a vertex (node);

*loop contributes to +1 to indegree and +1 to outdegree

directed-graphs-degree
_{*Note: the example was reduced to essentials, thats why some other nodes which should be connected to the ones displayed are excluded.}

In the example above:
- degree of the vertex AA can be denoted as:

$deg^-(AA) = 1$
$deg^+(AA) = 2$

- degree of the vertex BA can be denoted as:

$deg^-(BA) = 1$
$deg^+(BA) = 3$

Some other related concepts worth mentioning are:
a) Min In-Degree $\delta$_in -- the smallest indegree among all nodes in a graph;
b) Max In-Degree $\Delta$_in -- the largest indegree among all nodes in a graph;

a) Min Out-Degree $\delta$_out -- the smallest outdegree among all nodes in a graph;
b) Max Out-Degree $\Delta$_out -- the largest outdegree among all nodes in a graph;

a) Min Total Degree $\delta$_total -- the smallest degree among all nodes in a graph;
b) Max Total Degree $\Delta$_total -- the largest degree among all nodes in a graph.

If $deg^+(v) = deg^−(v)$, the graph is called a balanced directed graph:
graphs-equal-degree
_{*Note: the example was reduced to essentials, thats why some other nodes which should be connected to the one displayed are excluded.}

A vertex with $deg^−(v) = 0$ is called a source, as it is the origin of each of its outcoming edges. Similarly, a vertex with $deg^+(v) = 0$ is called a sink, since it is the end of each of its incoming edges:
degree
_{*Note: the example was reduced to essentials, thats why some other nodes which should be connected to the ones displayed are excluded.}

Families of Graphs¶

Path Graphs¶

Path is denoted as $P$_$n$ where _$n$ is a number of vertices (nodes) in a path.
$V = \{$ 0, 1, ..., n-1 $\}$
$E = \{$ (0, 1), (1, 2), ..., (n-2, n-1) $\}$

Undirected Path Graph¶

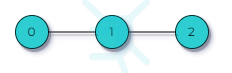
graphs-path
In the example above, the path can be denoted as $P$_$3$

Directed Path Graph¶

graphs-directed-path
In the example above, the path can be denoted as $P$_$4$

Cycle Graphs¶

Cycle is denoted as $C$_$n$ where _$n$ is a number of vertices (nodes) in a cycle.
They are somewhat related to paths. If you remove one of the edges on a cycle you are left with path.
$V = \{$ 0, 1, ..., n-1 $\}$
$E = \{$ (0, 1), (1, 2), ..., (n-2, n-1), (n-1, 0) $\}$

Undirected Cycle Graph¶

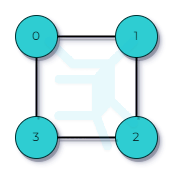
graphs-undirected-cycle
In the example above, the cycle can be denoted as $C$_$4$

Directed Cycle Graph¶

graphs-directed-cycle
In the example above, the cycle can be denoted as $C$_$3$

Complete Graphs¶

Complete graph is denoted as $K$_$n$ where _$n$ is a number of vertices (nodes) in a complete graph.
Complete graphs do not include multiple (parallel) edges and are undirected.
$V = \{$ 0, 1, ..., n-1 $\}$
$E = \{$ (0, 1), (0, 2), ..., (0, n-1), (1, 2), (1, 3), ..., (1, n-1), (2, 3), (2, 4), ..., (2, n-1), ... $\}$
graphs-complete
In the example above, the graph can be denoted as $K$_$5$

Tournament Graphs¶

Tournament graph is basically a directed complete graph.
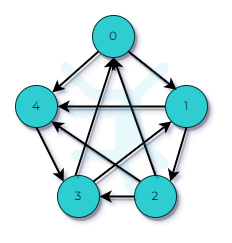
graphs-tournament
In the example above, the graph can be denoted as $K$_$5$

Star Graphs¶

Star graph is denoted as $S$_$n$ where _$n$ is a number of vertices (nodes) in a star graph.
$V = \{$ 0, 1, ..., n-1 $\}$
$E = \{$ (0, 1), (1, 2), ..., (0, n-1) $\}$

Undirected Star Graph¶

In the example above, the graph can be denoted as $S$_$5$

Directed Star Graph¶

In the example above, the graph can be denoted as $S$_$4$

Mathematical Representation of Graphs¶

Facebook: here nodes are accounts, and an edge (relationship) exists between them if the accounts are friends with each other. It's a 2-way relationship:

Adjacency List

Bob: Alice
Alice: Bob, Luna
Luna: Mike, Alice
Mike: Luna, Aurora, John
Aurora: Mike, John
John: Mike, Aurora

Adjacency Matrix $$ Facebook = \begin{bmatrix} BobBob & \color{#007FFF}BobAlice & BobLuna & BobMike & BobAurora & BobJohn \\ \color{#007FFF}AliceBob & AliceAlice & \color{#007FFF}AliceLuna & AliceMike & AliceAurora & AliceJohn \\ LunaBob & \color{#007FFF}LunaAlice & LunaLuna & \color{#007FFF}LunaMike & LunaAurora & LunaJohn \\ MikeBob & MikeAlice & \color{#007FFF}MikeLuna & MikeMike & \color{#007FFF}MikeAurora & \color{#007FFF}MikeJohn \\ AuroraBob & AuroraAlice & AuroraLuna & \color{#007FFF}AuroraMike & AuroraAurora & \color{#007FFF}AuroraJohn \\ JohnBob & JohnAlice & JohnLuna & \color{#007FFF}JohnMike & \color{#007FFF}JohnAurora & JohnJohn \end{bmatrix} = \begin{bmatrix} 0 & \color{#007FFF}1 & 0 & 0 & 0 & 0\\ \color{#007FFF}1 & 0 & \color{#007FFF}1 & 0 & 0 & 0\\ 0 & \color{#007FFF}1 & 0 & \color{#007FFF}1 & 0 & 0\\ 0 & 0 & \color{#007FFF}1 & 0 & \color{#007FFF}1 & \color{#007FFF}1\\ 0 & 0 & 0 & \color{#007FFF}1 & 0 & \color{#007FFF}1\\ 0 & 0 & 0 & \color{#007FFF}1 & \color{#007FFF}1 & 0 \end{bmatrix} $$

Instagram: accounts are nodes as well, and an edge exists if one account follows the other account. Moreover, when Mike follows Luna, but Luna doesn't follow Mike, then there is some direction to the "follow" relationship.

Adjacency List

Bob: Alice
Alice : Bob, Luna
Luna:
Mike: Luna, Aurora, John
Aurora: Mike, John
John:

Adjacency Matrix $$ Instagram = \begin{bmatrix} BobBob & \color{#FF9933}BobAlice & BobLuna & BobMike & BobAurora & BobJohn \\ \color{#FF9933}AliceBob & AliceAlice & \color{#FF9933}AliceLuna & AliceMike & AliceAurora & AliceJohn \\ LunaBob & LunaAlice & LunaLuna & LunaMike & LunaAurora & LunaJohn \\ MikeBob & MikeAlice & \color{#FF9933}MikeLuna & MikeMike & \color{#FF9933}MikeAurora & \color{#FF9933}MikeJohn \\ AuroraBob & AuroraAlice & AuroraLuna & \color{#FF9933}AuroraMike & AuroraAurora & \color{#FF9933}AuroraJohn \\ JohnBob & JohnAlice & JohnLuna & JohnMike & JohnAurora & JohnJohn \end{bmatrix} = \begin{bmatrix} 0 & \color{#FF9933}1 & 0 & 0 & 0 & 0\\ \color{#FF9933}1 & 0 & \color{#FF9933}1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & \color{#FF9933}1 & 0 & \color{#FF9933}1 & \color{#FF9933}1\\ 0 & 0 & 0 & \color{#FF9933}1 & 0 & \color{#FF9933}1\\ 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$

Example: Königsberg Bridge Problem¶

Can all seven bridges over the river Preger be traversed in a single trip without doubling back, with the additional requirement that the trip ends in the same place it began?

Answer: For a walk that crosses every edge exactly once to be possible, at most two vertices can have an odd number of edges attached to them. In fact there have to be either two vertices with an odd number of edges or none at all. In the Königsberg problem, however, all vertices have an odd number of edges attached to them, so a walk that crosses every bridge is impossible. (See Euler's solution)
python-graph-1
Vertices (landmasses): { $A$, $B$, $C$, $D$ }
Edges (bridges): { $AaB$, $AbB$, $AcC$, $AdC$, $AeD$, $BfD$, $CgD$ }
Degrees (bridges per landmass): $deg(A)=5$, $deg(B)=3$, $deg(C)=3$, $deg(D)=3$

The sum of the degrees of each landmass is even and is twice the number of the existing edges. In the example there are 7 bridges. When we add up the bridges of each landmass, we get 14, exactly twice of the number of bridges. The result follows the Handshaking Lemma.

Named Tuple (Königsberg Bridge Problem)¶

Despite this method being probably the best mathematical representation of a graph, it may not be the most convenient in some other cases.

In [1]:

from collections import namedtuple

In [2]:

Graph = namedtuple("Graph",["nodes","edges"])

In [3]:

nodes = ["A","B","C","D"]
edges = [
    ("A","B"),
    ("A","B"),
    ("A","C"),
    ("A","C"),
    ("A","D"),
    ("B","D"),
    ("C","D"),
]

G = Graph(nodes, edges)
print(G)

Graph(nodes=['A', 'B', 'C', 'D'], edges=[('A', 'B'), ('A', 'B'), ('A', 'C'), ('A', 'C'), ('A', 'D'), ('B', 'D'), ('C', 'D')])

Adjacency List (Königsberg Bridge Problem)¶

$A: B, B, C, C, D$
$B: A, A, D$
$C: A, A, D$
$D: A, B, C$

In [4]:

def adjacency_dict(graph):
    """
    Returns the adjacency list representation
    of the graph.
    """
    adj = {node: [] for node in graph.nodes}
    for edge in graph.edges:
        node1, node2 = edge[0], edge[1]
        adj[node1].append(node2)
        adj[node2].append(node1)
    return adj

In [5]:

adjacency_dict(G)

Out[5]:

{'A': ['B', 'B', 'C', 'C', 'D'],
 'B': ['A', 'A', 'D'],
 'C': ['A', 'A', 'D'],
 'D': ['A', 'B', 'C']}

It can be further improved by using integer instead of string node and edge values, and by adding the orientation parameter.

In [6]:

Graph = namedtuple("Graph",["nodes","edges","is_directed"])

In [7]:

G = Graph(
    nodes = range(4),
    edges = [
        (0,1),
        (0,1),
        (0,2),
        (0,2),
        (0,3),
        (1,3),
        (2,3),
    ],
    is_directed = False
)

print(G)

Graph(nodes=range(0, 4), edges=[(0, 1), (0, 1), (0, 2), (0, 2), (0, 3), (1, 3), (2, 3)], is_directed=False)

In [8]:

# Imporoved adjacency list function
def adjacency_dict(graph):
    """
    Returns the adjacency list representation
    of the graph.
    """
    adj = {node: [] for node in graph.nodes}
    for edge in graph.edges:
        node1, node2 = edge[0], edge[1]
        adj[node1].append(node2)
        if not graph.is_directed: # Added this line
            adj[node2].append(node1)
    return adj

In [9]:

adjacency_dict(G)

Out[9]:

{0: [1, 1, 2, 2, 3], 1: [0, 0, 3], 2: [0, 0, 3], 3: [0, 1, 2]}

Adjacency Matrix (Königsberg Bridge Problem)¶

$$ Bridges = \begin{bmatrix} AA & \color{#2DCDD2}AB & \color{#2DCDD2}AC & \color{#2DCDD2}AD \\ \color{#2DCDD2}BA & BB & BC & \color{#2DCDD2}BD \\ \color{#2DCDD2}CA & CB & CC & \color{#2DCDD2}CD \\ \color{#2DCDD2}DA & \color{#2DCDD2}DB & \color{#2DCDD2}DC & DD \end{bmatrix} = \begin{bmatrix} 0 & \color{#2DCDD2}2 & \color{#2DCDD2}2 & \color{#2DCDD2}1 \\ \color{#2DCDD2}2 & 0 & 0 & \color{#2DCDD2}1 \\ \color{#2DCDD2}2 & 0 & 0 & \color{#2DCDD2}1 \\ \color{#2DCDD2}1 & \color{#2DCDD2}1 & \color{#2DCDD2}1 & 0 \end{bmatrix} $$

In [10]:

Graph = namedtuple("Graph",["nodes","edges"])

In [11]:

nodes = ["A","B","C","D"]
edges = [
    ("A","B"),
    ("A","B"),
    ("A","C"),
    ("A","C"),
    ("A","D"),
    ("B","D"),
    ("C","D"),
]

G = Graph(nodes, edges)
print(G)

Graph(nodes=['A', 'B', 'C', 'D'], edges=[('A', 'B'), ('A', 'B'), ('A', 'C'), ('A', 'C'), ('A', 'D'), ('B', 'D'), ('C', 'D')])

In [12]:

def adjacency_matrix(graph):
    """
    Returns the adjacency matrix representation
    of the graph.
    Assumes that graph.nodes is equivalent to range(len(graph.nodes)).
    """
    adj = [[0 for node in graph.nodes] for node in graph.nodes]
    for edge in graph.edges:
        node1, node2 = edge[0], edge[1]
        adj[node1][node2] += 1
        adj[node2][node2] += 1
    return adj

In [13]:

adjacency_matrix(G)

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[13], line 1
----> 1 adjacency_matrix(G)

Cell In[12], line 10, in adjacency_matrix(graph)
      8 for edge in graph.edges:
      9     node1, node2 = edge[0], edge[1]
---> 10     adj[node1][node2] += 1
     11     adj[node2][node2] += 1
     12 return adj

TypeError: list indices must be integers or slices, not str

Since nodes are represented as string in this case, they should be relabled using integer in order to put them into a matrix:
A $\to$ 0
B $\to$ 1
C $\to$ 2
D $\to$ 3

In [14]:

nodes = range(4)
edges = [
    (0,1),
    (0,1),
    (0,2),
    (0,2),
    (0,3),
    (1,3),
    (2,3),
]

G = Graph(nodes, edges)
print(G)

Graph(nodes=range(0, 4), edges=[(0, 1), (0, 1), (0, 2), (0, 2), (0, 3), (1, 3), (2, 3)])

In [15]:

adjacency_matrix(G)

Out[15]:

[[0, 2, 2, 1], [0, 2, 0, 1], [0, 0, 2, 1], [0, 0, 0, 3]]

Again, this graph can be improved by adding the orientation parameter.

In [16]:

Graph = namedtuple("Graph",["nodes","edges","is_directed"])

In [17]:

G = Graph(
    nodes = range(4),
    edges = [
        (0,1),
        (0,1),
        (0,2),
        (0,2),
        (0,3),
        (1,3),
        (2,3),
    ],
    is_directed = False
)

print(G)

Graph(nodes=range(0, 4), edges=[(0, 1), (0, 1), (0, 2), (0, 2), (0, 3), (1, 3), (2, 3)], is_directed=False)

In [18]:

# Imporoved adjacency matrix function
def adjacency_matrix(graph):
    """
    Returns the adjacency matrix representation
    of the graph.
    Assumes that graph.nodes is equivalent to range(len(graph.nodes)).
    """
    adj = [[0 for node in graph.nodes] for node in graph.nodes]
    for edge in graph.edges:
        node1, node2 = edge[0], edge[1]
        adj[node1][node2] += 1
        if not graph.is_directed: # Added this line
            adj[node2][node1] += 1
    return adj

In [19]:

adjacency_matrix(G)

Out[19]:

[[0, 2, 2, 1], [2, 0, 0, 1], [2, 0, 0, 1], [1, 1, 1, 0]]

Adjacent List (Python)	vs.	Adjacent Matrix (Python)
* Can handle arbitrary hashable nodes.		* Only works for graphs whose nodes are integers.
* Good for graphs with few edges, uses less memory.		* Not a good choice for sparse graphs, uses most memory.

Degrees (Königsberg Bridge Problem)¶

In [20]:

Graph = namedtuple("Graph",["nodes","edges","is_directed"])

In [21]:

G = Graph(
    nodes = range(4),
    edges = [
        (0,1),
        (0,1),
        (0,2),
        (0,2),
        (0,3),
        (1,3),
        (2,3),
    ],
    is_directed = False
)

In [22]:

def degrees(graph):
    """
    Return a dictionary of degrees
    for each node in the graph.
    """ 
    adj_list = adjacency_dict(graph)
    degrees = {
        node: len(neighbors)
        for node, neighbors in adj_list.items()
    }
    return degrees

In [23]:

degrees(G)

Out[23]:

{0: 5, 1: 3, 2: 3, 3: 3}

(Python) Graph Visualization¶

In [24]:

from collections import namedtuple
from itertools import combinations # used in complete graph
from pyvis.network import Network

In [25]:

Graph = namedtuple("Graph",["nodes","edges","is_directed"])

(PyVis) Example Graph¶

In [26]:

# Instantiate a Network class
graph = Network(directed=False)

# Add vertices (nodes) to the network
graph.add_node(0, label="AAA") # '0' is an id, 'AAA' is a label diplayed in the visualization
graph.add_node(1, label="ABA")

# Add edges (lines) between vertices (nodes)
graph.add_edge(0,1)

# Save output in an html
graph.show(
    "html/example-graph.html", 
    notebook=False # notebook configuration, throws en error if not set to False 
)

html/example-graph.html

pyvis-undirected-graph

(PyVis) Generate Graphs¶

The validate_num_nodes() function is used within other functions to validate the input.

In [27]:

# Used within graph generating functions
def _validate_num_nodes(num_nodes):
    """
    Check whether or not 'num_nodes' is a
    positive integer, and raise a TypeError
    or ValueError if it is not.
    """
    if not isinstance(num_nodes, int):
        raise TypeError(f"num_nodes must be an integer; {type(num_nodes)=}")
    if num_nodes < 1:
        raise ValueError(f"num_nodes must be positive; {num_nodes=}")

Use with show_graph() to visualize the output.

In [28]:

def show_graph(graph, output_filename):
    """
    Saves an HTML file locally containing
    a visualization  of the graph, and returns
    a pyvis Network instance of the graph.
    """
    g = Network(directed=graph.is_directed)
    g.add_nodes(graph.nodes)
    g.add_edges(graph.edges)
    g.show("html/" + output_filename, notebook=False) # 'html' is a folder name
    return g

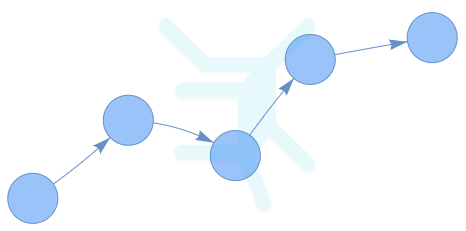
(PyVis) Path Graph¶

In [29]:

def path_graph(num_nodes, is_directed=False):
    """
    Return a Graph instance representing
    an undirected path in 'num_ndes' nodes.
    """
    _validate_num_nodes(num_nodes)
    nodes = range(num_nodes)
    edges = [(i, i+1) for i in range(num_nodes - 1)]
    return Graph(nodes, edges, is_directed=is_directed)

In [30]:

show_graph(
    path_graph(5, is_directed=True),
    "gen-path-graph.html"
)

html/gen-path-graph.html

Out[30]:

<class 'pyvis.network.Network'> |N|=5 |E|=4

gen-path-graph

(PyVis) Cycle Graph¶

In [31]:

def cycle_graph(num_nodes, is_directed=False):
    """
    Return a Graph instance representing
    an undirected cycle in 'num_ndes' nodes.
    """
    _validate_num_nodes(num_nodes)
    base_path = path_graph(num_nodes,is_directed) # uses path_graph() output
    base_path.edges.append((num_nodes - 1, 0))
    return base_path

In [32]:

show_graph(
    cycle_graph(10),
    "gen-cycle-graph.html"
)

html/gen-cycle-graph.html

Out[32]:

<class 'pyvis.network.Network'> |N|=10 |E|=10

gen-cycle-graph

(PyVis) Complete Graph¶

In [33]:

def complete_graph(num_nodes):
    """
    Return a Graph instance representing
    a complete graph in 'num_ndes' nodes.
    """
    _validate_num_nodes(num_nodes)
    nodes = range(num_nodes)
    edges = list(combinations(nodes, 2))
    # edges = []
    # for i in range(num_nodes - 1):
    #     for j in range(i + 1, num_nodes):
    #         edges.append(i, j)
    return Graph(nodes, edges, is_directed=False)

In [34]:

show_graph(
    complete_graph(10), 
    "gen-complete-graph.html"
)

html/gen-complete-graph.html

Out[34]:

<class 'pyvis.network.Network'> |N|=10 |E|=45

gen-complete-graph

(PyVis) Tournament Graph¶

In [35]:

def tournament_graph(num_nodes):
    """
    Return a Graph instance representing
    a complete graph in 'num_ndes' nodes.
    """
    _validate_num_nodes(num_nodes)
    nodes = range(num_nodes)
    edges = list(combinations(nodes, 2))
    return Graph(nodes, edges, is_directed=True)

In [36]:

show_graph(
    tournament_graph(5), 
    "gen-tournament-graph.html"
)

html/gen-tournament-graph.html

Out[36]:

<class 'pyvis.network.Network'> |N|=5 |E|=10

gen-tournament-graph

(PyVis) Star Graph¶

In [37]:

def star_graph(num_nodes, is_directed=False):
    """
    Return a Graph instance representing
    an undirected cycle in 'num_ndes' nodes.
    """
    _validate_num_nodes(num_nodes)
    nodes = range(num_nodes)
    edges = [(0,i) for i in range(1, num_nodes)]
    return Graph(nodes, edges, is_directed=is_directed)

In [38]:

show_graph(
    star_graph(20), 
    "gen-star-graph.html"
)

html/gen-star-graph.html

Out[38]:

<class 'pyvis.network.Network'> |N|=20 |E|=19

(PyVis) Additional Style Options¶

(PyVis) FrankenGraph¶

In [39]:

# Assign color values to variables
background_color = '#f5f5f5'
font_color_light = '#111111'
font_color_dark = '#0b0c10'
node_color_not_highlighted = '#f5f5f5'
node_color_highlighted = '#26c8cd'
border_color = '#333333'

# Base64 encoded image for the node
node_image_base64 = 'data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wCEAAoGCBYVExcVFRUXFxcZGR8cGhkaGBwfHBsfIRohGiAgGiMjIysjHyMqIxwcJTYkKCwyMjIyIyE3PDcwOysxMzEBCwsLDw4PHRERHTEpISkxMTEzMzE5MzExMTEzMTExMTExMTExMTExMTExMTExMTExMTExMTExMTExMTExMTExMf/AABEIAOEA4QMBIgACEQEDEQH/xAAcAAEAAgMBAQEAAAAAAAAAAAAABQYDBAcCAQj/xAA/EAACAQIEAwcBBgQFAwUBAAABAhEAAwQSITEFQVEGEyIyYXGBkQcUI0JSoWKxwdEzcoKS8FOi4RUkY5OyQ//EABkBAAMBAQEAAAAAAAAAAAAAAAACAwEEBf/EACYRAAICAgMAAQQCAwAAAAAAAAABAhEDIRIxQVEiYXGxMvEEE9H/2gAMAwEAAhEDEQA/AOy0pSgBSlKAFKUoAUpSgBSlKAFKwYnEJbGZ3VB1ZgB+9V3iXb3AWtDfDnpbBb+WlAFppXO8X9rGGXyWrr++Vf61pD7WwxhMIx97g/tW0zLR1GlcuP2tQSGwjaCdLg/tW9Y+1XDnR7F5dpjK0T8iijTodKquD7fYF4Bvd2TyuKV/farFg8bbuCbdxHHVWB/lWAbFKUoAUpSgBSlKAFKUoAUpSgBSlKAFKUoAUpSgBSlKAFK0ONcVtYa0bt5wijrufQDma5J2w7fYnE5kwoNu1zg/iOPf8vsK1KzG6OidqO2uEwcq9zPc/wCmmrfPJfmubcb+07F3864cLYUc/M8TEydB8CqxhOEuytcIm3ALE7gnn12menyKluG8FbPcXICzWDlU6ZiGBA9JC1RQJPIQeOuXrjzduPcLEFczEk9RG0xr9akbOBAAdh5WysI2EwTHTyt7H3rFi7JNs5SSc4YHUERIHKRpz6gjlVi7POj3zmYRlTvFAGrjKMwH8Wa4J6N7VqgK8hCY3stcdHMEG2M0yII3K6azpI60wvCSBduElQWyz+kqM3QyWBgVdra/iFcp7sWdSYymGDKNOYAjXlFY+IK1uzfK/wDTKqAAfEtswTykBFP1qihsm8mtFVeygxJlkLAEMoYEy0EgjkQB8E8q1sTgnFzxqVOj5RyB8o+gFeLWDVHtXUUvbCM7OdZuANmU/BUidTFTKm5cCN//AEYW2ZdNVjMdOQj+tT4lXPorwwfeOpltWOXSVmM2vP42nSsd13t3m7pmtlSACrQYEySQeoq48UbDraVjKXIjUQFJjWesRHQTUHa4RaRSzvKNlM9Y8W+wEmfkClGUiY7P/aFjLSWzc/GRhtcEMBrrmHtuRXQ+zXbjC4qFzG1cP5Lmk/5Tsf51yHChrt3PBFlF8IAgEcvrHxX3EOptG6FOpKKp0JPI+ggT12rf9dhzP0NSuNdlO1+JwwRbs3LZ0yMZcdMp3GnWupcD41axSZ7Tgx5l/Mp6EUkotDxkmSdKUpRhSlKAFKUoAUpSgBSlKAFKUoAVB9qu0dvBpLeK43kQHU+p6D1r52u7QJg7cmDcbS2k6k9T6CuXYi3cvMb11szudzsDuo9F0iKA8I7tHdxGLu95dfNPkQ+VeoUdNakuCcMSVYpBZTGuiukEjTQggiOmtWvAcBN62h0UqwJHUcx7VD9pcT3V8rb0Nu4vdjZZjIyOYgFhAB22nSunHFNHHklJP8mHihS0cTbBADtnXKJU6d6AYBIlV5A7DTWqnxbGvh7+jZkzTaeQwjUQDOo8ylffmatHFLWcEoHVwDBGh0IUg6GGSB6SFOzHLD4rDHEWhbTJ3tqc1uCFImQcupEMQPTMCCRtZrVInjXrNPiXEHuJmVVtkAg5Z1Gik6k7SDOhg9RNWbsbhraXbmYg/iaH+FnzpPpDrPselVTA4ebJRgdV16hScpB9fMOXkG9YuzvESC+f/EUw/VlAKEgfqXQ/GnSpurVjuLrRe+Lux7u2TGa6pcA7rLMF3/8Aig+hNVrHcbuph8NLBjcY3G6lC/dkH/fz6VOpinu2EuKF7y0QLgjUlW15+Vlz/wC6q5xbhxuIq21J7u81sdO7uFSpHOJUnTqPSml06EgqpM84LDDPcwwYlS9tlGvK6tsz7oJj1qcwbBMOt4qWuMMi+rANbWf2mtfslbz4i60ZjL5Z3hLoOkekVK4XDnzPsp25A5vDl9dfbX0pUvRpPwqHG1N+4M5LiXgakQHYTHInT9hUp/6MSlq1smbO/SJz5R6a/RfWt7g/CAWzvLZTA031gfUgn21p2q4oLDiyhL338TGYS2oEkk/5RsOntSqPrDl5E0+0HFlsl7dpQcgMk6IhIhV9W206a1WLXHL7qMzBh3gTJkXKdpy6SDqOfrWTtai9+2cxaJDoogM5ZA512A1AzHkAK+8BwTXQ1zKFt20IQcpYhZB9ATruYPSj2kVX8bZZuGYXS9cZvMe8t6SYIhfbTl0qL4ZdvWcQHslkyxqu0SJzfljfTc1s4nFlrSLbWYRUQjViANGA5nlz/aveDwpkWnMqjBnbcawMo/jhen5j0p6sRM6j2J7VJjLYDju7omUOzQYzJ1FWauE8UxhW+otnuntgHMumRUBYwPSY21NdR7FdpBirYVxkvKoLIdCRyYe+8Vzzx1s6ITvTLNSlKmUFKUoAUpSgBSlKAFaXGuIph7LXbhhVHyTyA9TW7XKvtE4q2JvGzbJ7qydY/M/M+w2+tAEDdxFzFYhsVd8Q2CD8ig6Aa6+tW7gXDbVwEuwKTMNsddiPccqjOwPChckkQR4swMBuQkDSfUfNbnFSEu+GALf5F3Jndf7cjPIVWMLZz5Mjirq0TNzHdw6Lall2jcD09J5eunOoDtRh1vtcuITMAusaGRH/AA+/Ssvbe6y27JskKGUyx18QgqpJ2ETr7Gd6hODcZ+8OQ3huKhtuvMg7yOqnURuI+OjHFaZy5pT3XS2aGJv3EeFaGMSlw+C5rClWGqXY/NprJnlWbG4kQb1uUuoNVIGZ4/I67aSJI3DSIJIFGxfe4Z3RWK5SQV5dMyg7ieY167TUnwTiheATkuCMpmQYBP8AePpsdDlsu46JrHlczFWARmD6flDgq/xBzgaRvpVTa4bWLuNEQS0dQTmj4mPirLiUKqHGZQCQRuFBnMI6QWHsB1qM4nwt2IKakKcp3BUiCrR0BAPwedJN2jYP5Ld2RMYgpIC3bAME6ZgSv8lU/FR/ELrWcfacyLbRacdAjEBh7Qrf6SK3OzPD7jXsPcVlAVcrEnQDLmb/APLfvXvjWDtY5h3d2GtXQrd4AqmWklSxBmAdDqRttWcnX3F4bvw99kgLGJCsdGuXLep1JzuQPXSPpVot4QvdOUfm35QMu/8AtP1rQscKsd4mIN0XO7ZsqJLZnhF1PLLA+T1rJju0rtautlZbdsGMrAMYZkEH+Jk0PrS8mbwVH3jF77nh3eBmGiL1Ywqj6D41iuYPmZ7t1mzBbSIXOzO6q7+8kmfc8q6F2gQ3+G2mGZrgCMZ1bxECSeniMkbDWonhfZ5rjWwfw7NoK0EDO7EZQWH5RAGrRrmAnetk7qhca43ZGYvs5cxSYZxlVRh1W47GMrLKmR1iKlDhMltcNhzltKw726QQHb9Kczp0k6n4s2I4hbtsliyFLg5TNssskFoJkQfC2sRXOO2HH7l286Wye7DFYTdoMGY8q7wNJGp3qkVStmNuTpdEt92t22ZVuhQfNDILkamFUkZFiecmdtKy4QAMlwrPi/DRZIA5licoJPXXkIiqbhsDcRrYRc193BUKJyCdzyEnTXo1XL7sbMvLXm5kyYO0WtIJ+CY6CtTNao38db8SqUVS4JuQZ8OYkKTqWknUbaCvVljbuLctt+KWLlvT9J9OX9BWTDcNa/cJZm7oedTKyY1MDU6RLNz29JLA21RWLp3a7KdpA5AcgYJ1pZ00NDsvHAeKLiLQddDsy81NSVcz4JxFsLiC9wFbd1oYE6AcmjlB5b10oGdRXNJUzpi7PVKUpRhSlKAFKUoAhO2fFDh8OzL538Ce55/Ak1z7s9w9S57w93kGcyd1/N6yJH113qU7ZcS7zHpbzL3dmA4JiS0ZvaARrWLiJuWiyPdyW1WFuKUVrgPhytI8RAjUagaVXHDk6IZsnBWeO0HGLi4bNhbbCFJjTxAGTAEtqoJ35ajWqeeKXXh2ukDRspChkkkRlAB5zroeR5Ddwji3mUC4lzUIzuGV42VmABEywBzGOtVi6LjlmJbOhKkN51BJlGnzQZErMyZHTplFR0jnxpyTcnZP8O7XL4rGMURO4GmuoaNxP6hWfH4O2twYiyVUgSrAk7flOpz7DQ6671WUe1dAW/4HUQpJgxHJtR8HStrg1k2byoXD22YFlOYGJEMJ8JIB1ymSJ0pIS8HlH1G3xnDjGKbtpVD6Z7TzBMb22ABB5TpsJHmirXMPkJ8Loy7o2p0OuU819dx6iumdqOK3LDAW0AGYOYQA92VAhSZDENMmNis8phMXxq6lzu7gtYi0wzWzdQeNPcaZgNxHI/GZE+zYS+n9E52KwpxVkKQM2XUk7qdfEfiPYis/AeA3Ld0BXtvaS5BLEqbYhs6kHltB2I5AAVj4bxQHC3BZFuwuz90DmiCAQd+sRuYHWoW5ii0M7FLk92xWPxQFJQGNCSrPBiCR0gFKaV2b34Ty9zZxRK3c1u6GGg8IYatrOsqx0+m9V3B4WEuKT+JmVG5+NWTxj0IMyOprybltFBJ8GcNA/KR0nUc99gV6Vlu8aS33yHxk2xkOxBAyzoJmAfoKJWwi0lRZ+EurZdMqzm9QHQ3Z9DpB01YE1C4AM+DuOwKi49uAP0q5ORf2UE+k1HcI42EnMRLq0z6Bh9PEwA9am+EcSRMPbgrK+JVPlzkQNOgBBnrrU5W2kVjximyzYlSbKpb0uDKgCwPF0HoACPk1X8Gj27q2s/esc126SQEAGgVQABBfTMRL5SfKNfVvGOMMgtkl7sIhOhCxq5jbQsJ3Bjep/BYC3as93uWALHbNoTr9CY5D31rGW0SlHTKDexvd3Ljljmu2zbVgvkOsMOfhJYkzoWUdaYHgeRUZiChCm0EUk3ZOiKDGuhBk8mJhdK28baLYqAVZiPw1jw2UG7RzOpJ9SJNTN/iJt4abYJysyWrj6sSy53YToEgZpOhOmg0p4yUtk3cVVEJintYAF7hFzFPqVDeG0p2BMdNNpaDEAVVcbxx7j53uuTEKnlVQf0KNvcmfet29hUfNcuXEdSSdToxiSzNzPtm9xpUv2W7NtfYOS1uyCCdAmcDkoAmDzJM/Wmv01JR77LB9mtnucOty6YLy3i3yny5iddpOvWpLjrPcuBE0RYYtlJJ/yjYEA7n1rR4tYus0+FLYICiRKqJEzOhO0nQa7zUTxPENddi2JyBTrALaToqgHmQeRJj3ojDdg56o2O0F5RbRLeZ/yzlU6zrJPOTyB+Kuv2b8X77Dm2x/EsnI0mTG6z8afFUriGJti0TmyKmmYxLaHbkDP8qx9g+KC3jEZSFtMMjn8rliMpHUgx+9Zkx3EbHOpHZKUpXGdYpSlACsWJuhEZzsqkn4E1lqv/aBiu7wVyDBeEB/zGP5TQDOeYXhputcv3XVUZszkHxiTIHUDlMH+ZHrtBxNlZVt3AllVULmMi4cuYlZ55hueXqasODs3LlgAQCugQwUuA8nWRJETPrVZ4vhLV0MMO9sEEa5CxmZGbMCQNxKkR712Yto4P8AIqM99P5POI40cy27rZ7TiQ4VNxsJXn8cvg6eJwpuIPFtM95EFc0gq6ibexAzeExqNai8VhMjyQ8aBkCgqWBifN4FJmJ1AMba16tYi7bCRbORpgBlPpm1YkHcSInnO1Ny8ZqSW0RvGOE3FIAMnnnIMjl4/K3vpNYsLduWoWHyj8syB6ppKnWYH7VZABeIAt5Rp4QRInSQu40jVHn0OorJj+EPaRXuYgYdCYUPbGY6kwCYkn2kDkKVxT2huXjMnEMWb+FsO1vvApuWbm4bk66/5ef6spmo/hGCIULcLPaPkLQtxOc66EeonWdDqDvYniyNbXCLnslNVuq5DM06vIMZT18pBjSQawoMyPavE96p8F1YVgN/GuzDXcb9CQDWS+wR12eLGEey2ZZe2xKgrsyturzGRoAYA8wIOxqJ4zxBFV1Qgo4UgkxBTUZTuCOWmgYD8tesdxN7QKZ86HTvF80zHiBEk/X2qm4zEM7Ek86m3GKoaKlOX2Nq7xe4QQDAYQ3Rp5xy35VqNi3JBnbb6zWCvlRtnQopeGa1iGUghiCBA9q3sJxZlGVixB0MGI9vioulFs1pMu+A7QMAGUjbnrlH6R1Y9PXpVswHE2uyveZNNWiXiRKrrDMYA+o1rjyMQZG4q5dkuIZjElREMQRMR5VzE6e+/Q7UznoVQ2dT4fhLQAt2tCQWuGc3/wBrbdfDMTy0qvcS4hYLNZt2/vCAyQ6qUdwBLAkExAAmVQACJ0FSvBcHFrux3j2yZZVEZgds7MfL/Co5eusrhMKqMs20QvACrLEa/qIAB9VWiE/ELOCX1GnwLBBbJxGItWYMJZtpaynMWOxYTHqRoAzHoIHtF2pa4DZwxYsshnsoSoOxCseh0zRrvptVt7TG415FRLpt29Mq5VQysEuzAzv+2+9QGLwRtqyILNoR4XJa6w65VAVF9xv610wV7ZyTkuVELwnFGyjfeDPebWnJdiZGp5sTAgcoHxKNi2WAtoWRAOVhZTU8yS0g+4qBW6tm6/dq9y5Ed/cUqVJ3yA+Ub6wTHOo4YlwQZzMCYMWyD6xIMDTVufWrJCk1jrOe5L+M7oqmbVsEHxXG0UjTlzqOTPnXO4ayDmUyJL76Rtry9K+Y64X8DG64dgWYMdguwgREzpWvwxDcI8IS2h2aDtPzIkVRq0atI77wPGC9Yt3RrmUH52P71v1UvswvThCpbNkdvofEP61ba8qSptHfF3FMUpSsGFUX7YMRlsWV5Ndk+wU/3q9Vz37XFzPhAZjM5gAmdAIgb00exZdG1w60l+xl0DoBDBgWByyGIgdeevOoDBs9u5l7r+IsFXNcnfPAgQd/epLhNnMp/DyHL4VS6FdiZ0hZRdNJIET1qPa3cRxpctnKQR3oYnkCZEjX+RroxurRx51yafphs4UXrhKW9yxMsAqjOTsIMVocQ4jYsErmGcaMVVmcHbXcL/qBnT0qRxLrYGigNv54LT6kbb1UuN4YK3eLdt2rbt5u78fUhmyknnAPTpT8qQsIW9syYbtDae7Ge4GJAUlAVnYAwJjQbj6VMdscSl1kS7JKKCY1CyFGUnKyrsSJgagSKr/aF2wlwdxatKrDMl8jO7iBqCYVT6Cq1nVmLm85diSW13JOpIaf2NLKfFUUUFJqS6LB91iAhVlk5F5qTzTQL11WT9azX3V1CXLiAqPMvpyMfTQzvtWlwTGXZgFLm0K5XWByOh+s/Nb3HFsG0Xfw3QYhSGbnpoBpy8R9NaWLvo2Win8ZbxRmJPOf213I9SajK2McwLmAw/zb/wDiteoSds6YKooUpSlGFKUoAVucJxHd3FYiddv61p1lwp8a7b89vmgDsHZTHvcgBs0iMqtAH0821WvEu6W5D93AGYmDp6ZyT+3SqB2P4iAAjXCh56TEdCFjL/ERp9Kt+KurdRkF2w3RWdZXToSMxmDJk+uulIJXsnk60jFf4v8AerK2/vireUxmWALomAGAJyNr/wA5RHGuC3LfiuYe7dEaFLkrHw0zJ/TrHKojHcBultcMHbk1u1bUf7muMvzFTfAL+KwxyvdgGMtot3sa7A5QR0MZgPSrrktI55KPbKxfxg1/9rl1iW1bb/L4d/2NZOH4FnErYNsqNHZDlPoVIBJPJhMdK7VxHBWgAzslvSTJA96jreGw7/4dxX/ysAR9INMsy+DHjadKjnNns03eC5euO5BEIpMj3PIfAqWbChlIIVQTy/qfn9zVu4jhrS291Azawd+UQKg8beUW2AXnoSdBvTLI5LSElCntkn9mbZXvW+QCkfEirvXPPs2uE4q54wwNrYcoYb10SuPIqkduN3EUpSkHFc7+15RnwpO0uJ6bV0SqR9rNr8Ky/wCm7H1X/wAVqMasxcA1NrIQRkAJnxGD02+vpzk1i7V2igGVTmOpgjXWSDAnn/PrXvsBcDSs6gE7knXTn5R6b1KYu2HvAAEKuhnnz9eu1UUqYkoXEofEsDduKQwALrEKubKT6mZ9orWwHZ9banxZf1AIIPoQGAmeXI/FWPtLxRwz27SoMvMtAOmuY65Y5FgAT81Qe02GnxXL9205gAXQjJ7IyRA13j5NdD2rZyQW3FPVlqGFtuptXu7NogZQLYGQ9RBPLr0qvY7guEsXGRrdwsIPg8pBEyCzKCI11PIiqzYxYtnwX3fQ7k5D6FTv7GpvhnanEeG2ALy7ZTaJHtIY9KRzj6iihJbTN/h+KtrpawzqJnVVZj0gy0H0BmsPaJSEJe1dB1gvcyke4kk+gmPpW3h8Zae4EFv7neYSXUK1ptSIubsu48p0nXpWziOD3gD3jW7lyTMqANBvMZngZegrUzHVWcoxPmOhHuZrFU32k4c9tyzBpOpJAj/nwKhK5pKmdUJKUbQpSlKMKUpQArJYUlgB1rHUjwLDd5cAy59dVmNPQ9aAL12QMSrplMDyKqsfUhjr7+9dEtqxWRat7QCUGadfMCQo+G9hVX7LcNDWz3pQouonRl9mH8pirGOD/hg2NGiAXk6bQxXQ/Iq6j8ohLIvCuYnG44N/gq0nzLcu2wfaS0e+lTfZvh622bEOtzOsLbF1zdh2EypgtAg7Rzkc60cXgcQAMt6wDrmTNmG+/iX4ipjDYC6ME0qnehg34ZIU+EpJAJGk6x9KprqyMrq0jBxni6BYuNdeN2ZVBHrBQab6zpUDjL1qQyXCOY/h9hOhrDxnvLT95eud0mUQVN46xqP0kHlIqKvNauAMtzvFiD4En/UMuYe9XgktIhV7Za/v4YBgZLAEn1AifSsV6WEiY+la/C0iyFRYGYkLziBr1r5iX8JA0/5zpuNdCXsmPsvT/wB3dPS10jdh/aulVzv7JLR7zEMeQVfqSTXRK8/L/NnpYv4IUpSplRVa+0nD58DcMTkKv9Dr+xNWWtfiOGF209s7OpU/IigDmPYfibB7dsHrIAGg6nmN/wC8VduLYpbdi5cYquVfNpzMA+nvXLuzl17d1rM92wbKXA8Uq0QJMDaZ9qseIxLEOsotpyDcdlzEkeKVj8/hBAjlOlVhFNkcmRxiyo8duRDXi1nxN3bK4WQQGJCliHEEAOrDNziIrSwRLAgXGuKWykpbi3mJ8uUDLdcnaFJncwKmOKcORyO6vO6jdXnXTeMuupmefrXnEPctqbdtT3kAF2ypkUjULB3MSdenlgA9EluyEJLjSK7jMKttgrKqtGkhS28eOAQdtlkV8wS3CZBZ43BYBANpMHQb6EVY+F9mDdGa4MzNoFUgTA/O+pOaJIE6HlvW1jHtWgttVFy6dFtWoUK3qdSD76anQDaco2Mpo+cDwVq9cW3cknMoZQMigaCYA2AnUsTtoJrZ7QPir1181u7ZtBsqZTllBMeIExMDwgf+MGKvJhLZuYq4tt21S1Z0fSNM0ltTudBtThva7FXBNu2ESYBuBnZuvMCPk+9Tm5RVf2Pj4vf9EJxfgIC5RBc7r4ix/wBPnJjm23Ic6ovFcCbTlT8SIMeo5V23jdwrauOtpLd0hRmtiGfOYy6aqfM2hmBvVCx/D1KvcY5pbKSASXO2VZ6tKiB+VidDScX6Clxeig0qVxPCHAkDfZdyR19t46xWhew7LGYHUT8UpdMw0rKlhiQApkxHrO31rdt8Iclh+mJPvz9p0oNNLDWS7BRzq6dlOFKHVXB5SNJBJjMu0j0memugx9muDgXVGqk+Ehhsw1/fcex6GuiWuDW5VYyHVQCZKuFnwj8ykAeHmNtpqkEJN0bvD8ILLBhDrsxXzdNQNWHxPWtbjuL7q4WVlMr4SwAD8wodYE/wsRqRrXvF3ALRzlrTKBmKn/DBOjKdntE9fLUVh2uJ+HeKX7ZkZhpkI/6gJggjeSMpjSNasmc8lZEYnj1tWztYulYlx3zXMv5Z7u4WXL/EjiNtOdk+z9RevXSLmbD3LbHKpYoJIEa+RhBGXfbU6Vhv8DwguIBafNkF0gMyqFhtFgzMAjKAAdtYrU7Mdp7Svks2VsWswLQ6g9Abi8xtrLEVjUkZyi/Ddu9mClxlsX2VDMp3Yb2jUA8tx19IxrwqxY1e2LlzchbcLPWOvzVlxDC4M9pyjyGiZHxzAP7V8uXCCFdUOaSx2nbbr7UymxeCfv8AwgU4mm8FSOo/4RWjxXEaFhzH7bVOY/u2XMUgnkCNRrvVV41e5Lt6VdNNXRBxalV2X77KLEYZ7kf4lw/RRH96udRnZjBdzhbNvmqCfc6n9zUnXnzdybPTgqikKUpSjClKUAcZ+0vBvh+I50MJiAGGg80gPy9AfmpDFcUCjKkZ+RILannGuu256bDe3/aNwj7xhSVE3LX4iRvoPEB7j+lcu4bxZ4zm5ctBiAoXzS2gLAgiBp9eVVgyU46LNw/vbmVTcZo8V1vJCzGgBJMnMABEmKlsJw5fI2ugOY65gdQZO+510FY+zVnvPw2JYmGvORGaBAWRA11mOXTStXthxF1CjxhWciAQDcXdVVd/EQY9CAelVb5aOeK4bqzJxm7ct/hYZQoOjXTsoO4QbSepqDwtm3hEuX2YROjAglyToAT8a9fk15Ae9eFtiYnxINvWf/jHhAA8xMmeUV2+zXLyWkV2t21LBLaZsxMgToYOhOo3J9Ke1GJOnKdEPc4q128bgRELb3GHeOqjbKX8I9IAHvNT3AcK129be5mC7jvGOsaAidYmBy1PtVYwdp8+ZtAjaW1IbxTpnbUHLoT4iZ00mrBhEv3MRbQBgqvbB5KEQi4Y5mSFHr4q503ytnVKKqkeOLcXL3LzMrZLTlLa6jPddiojq0KWLHUAAAAGpDgvCjcZe+he6ts0bBXZROUD8ttQiiOYNTnFOCW1i+Mhi6zm2xibrFVzE6kjQCAJ1PWq3wy1cuXCqNn713FxyBlOjrcI3i2GbTXUzudyUb6NhNLs3cFhgwWLcm41yAQZNtEgTO0sQYqPx/C7dqzaZpaXS2JGhXMQT/qOc+wqd7K8StFmW2juLNwobjAHNqxLRpEtO2u3KsnbnBNcs2TbBe33qK+WfCTpmI35wPf1qTjSv0otuvCAvdnBbw1zOAxtoolSSQqvIPTTxn42rDhLVq5aI1DsrW8wHr3lto5yVg1dr6XLj3EAtCRNu0W8bASCG0g5hB6/vUb2M4bbOJuYdgSq+NJ8wUNqp9pyn1GlHLqjYxSvl2R1zhzXFU2rbnOFV8oI7u6rErcGh0BA1HJmNT6C9dtBnRVU2wMQt3MgV00LofynQEESNBrzqUxeNbuHOG0Nm4oFtANbS6EKOpXxDc6CN6hMFxg422+HuuLWJUoyspItuy+JT7GCCN4zRqulYxknZOWSMlSNCxj7r5e7yYpAGVxGW4AwjxIwzEEc1meY2NaOH4Vfe5OGt3kYea1eRgCBpAeMjiOsmOleu3WXDXg/dFFYauh1RtTy5Droeh0rFge12KtBYuNcts0J3pCk+isBHw+vrVmnZBNNaLTgOFX8ObDsvgl7bpIJtqSLluORCvmWOhHSqze4I2He9dSIQN3UBs4a4+RSREQgacwJ2FSnBu2FlruV2uWbjmPGxKlp/KTIGvIkdIq4dwtwMRAducAhh7HnSylx7CMHL7fY5VwLiN1cx78OzTkk5mDzoWMCEYqVPWferfjcULqWgyEZ1DCJ0kAypG29YL3Y3D276XZNsK3kVoQmcwGu2p8tZWxjd82YgwIVRAgco57dapH6toWf0qmYbto2gQzSDtNafZTAfecZbXXIjZm6Quv7mBWLtDjGZRA02gmCauf2UcNZMOb9wQ13ygiCLY2+u/0rcs3GG+xcOPlK/C7UpSuE9AUpSgBSlKAFcb7Z8H+649CqDurzFkYgHI3NRPljU6f0rslRfaThCYqw1ptDurc1YbEVqZjKH2a4xlvEu+dU3PpzPr6V74wjO7HIoLEqr6llHIzJCfEHpXPriXcJiXtusXUbY/m1JBB/Sd6u3Asdaud33hJKKW8TmSQpJIGg09etVhKjnyQbMCW2tIwt/wCJd8Fo/JhyNTrLNqdiOZmoDizok2LI7xgYLsS8yZJ5gsZ+kCrNxEXHNwAhfCJuAQtm3GeCeZ1UEjeNPTV4PgrdoOLSkmF/EfQkmSTp5EUAnr1JqrVkYyr8mvwLs/cFtQxCsdXEbFjqSNNco06HWrPh+HW8Nbd7Ylm5nXxbAE/0GwpjcWLWGS4sqH0WRJ12IHtqJrFxTF93atqBLXSSJ2kCJn4n6dayMAnOvyRmPvrbQ3GuKQgGp8oJ5mN21MKOoqL4nxcvesWrSm2ty4t11Bhnm5pm6KxM5em87Vm7T4VLHdJdf8O3bDqu/eXWJJZusAE+gJ5gVodicK9282NuKcssEkRLHwrlHRQD8TEU0tukbBcY2y1cLwtvCpcyiQC9wz7yP6D2qE7P8ce0MY58QW2buVgSmYeEAek8h00qX7QX4tJZByteLBid9AQo02MiqphHYYTF3l0AW3aQHYw869czsZ945Vk4qjYSl8m3fR3dfxG77w3Q0kFmKB2iOWbQcoB5Vbuy3EPvCm4yqL627lsuNIOhEj1GVh0rn74ju7eGuZtRaCr6wuseu/TWpnszxEWcfcTdbruY5TJI/wC0x8+lSSXIo2+J44LxA4fuluu6rca5hmIMNbNtiEed51yg8x7CnGry57i4mbeItlIxFvZiDmtu6DcSNSOR5Ctb7UMMbT2317ty6trpmJVwfRohgeq/XB22xYFy2XzS9hBdjX8q5iBtmUkb8gRVG9NCRSbT+S68dsjEWluoFufhwyiCDC8vqQDy0PJgedXuFBFZlctaeQ1siXt6GJ5EiQQdDt6gy/2c8aa2z2ywNvRkIkQDdFthB21cNHoa3u2lpVvnL/h3VICjdbg8Rgesg+5b1p47EacXRTEtXCozeLMIkiVLDRWE8mAyz1FXT7PO0rEjD3T4x/hkjzKBsfUD+VUtWe2ctwtlnwkEkDrrW+MY9q8GKI4RlIcCG35+u4pnBSVDc6dnY+MWUuJknKxEg+u+3MehqrWfw84dm01KMBEE/lO4ipzHpFy3dzEDuwCPWdP+e1VXj+OuYi53VtiTcAUpl39QeR1H0qePSrwMu5X7+zBwPAvjsbkj8FNX5EL09Sdq7JaQKAoEACAOgFQ/ZDggwlgL5naC7dTH8hU5XPknyZ044cUKUpSFBSlKAFKUoAUpSgCpfaD2SGMthrZCX7fkbkw/Q3p0PKuI4PFXbV+6l0G26IyMpGozeE/9pOvtX6bqo9vuxlvGL3ihUvqNGjRwNcr+nrypk6FashOzGK7zOqKDmVdX0WfNlge+p56dKWuElFuqtwywOdiAPMD4bSjyCSYLSTvVJweNu4PEFLqNadB4gzQsSdV5NM7+1WTD4y1dvLlLBcwd2zHzaMVI2jKN+WlUhLxkMmNdoxY17mIS0gBhLgLN+XRgwVT7AjMNBFbd5u9v+HVbZy2y2gJYwSuh0VTHqdOtWTHYuzbskFc+kaAbE5QBr7VXOyd1r+JbIMllCc5ZQD4Z0GkKoPzprV+Wro53HdWZ+2PB7V25Zu3S75EZcikA3M8gBvjNqD/OtLEYqGS14QVykqnltgaDMdtfIoG8E8637mKR75a2Va3l8LchndRM7bMrCqi/4bBc4LIyXrrawzQWQFo2VcjZRyNamooFcpb6PXFMb3uIDLJRWyKRuJganlqxO22prLxgH/0zEHQL3wVMo0lLn8i4J5aGq7hsSYfu0IVW7wCNXViIgbmKu+PwIPCArg6AXXXnIIusPSTInlNQlPbRbhSTOf4xR3Nu2WzMgtwI0UspYgHn5l+orLex5S+5P5bkjqIy2/qfFWLvDct3XceNbguHUAZc0wOYjUAchWO9cW+6Zd2ZNehzCJ/3N80rLJqjrXH79stYS6oKXhz2zggoddBJIE+1UjjuDFy41ob5i6MfMsmPDOuhlWHWD6Cy9v7YNu0mg7sAyTEAmDH7VU+F3nvGy5YyrRmO7aOPqQq/7R0qyejmSps0OCGPvOdQlxLJ2gAsLtszpsdJPLfarNxzDfeLTOWKzldWABYaEyBzGrc9dOlVgcQt2792UJlmUxJzhpVlP9+tSVu5d7khSQLRyoRElGgwdIO/MU8F4E5es0bzyD3jOr6DNkzWn5TIg7DmND9K8AN32UqGLxlMNBM6e4rL92NyNwd5jwk+onRv51u4S06OluyGuXHfkfLylV/nVeifJPS7LX2t4qTFq3LkJlAXmdNvWYirN9n3Zg4de+va3nGx/IDy/wAx5197E9ku4/Gvw95jIG62/b19at9cWTIq4x6OrHjd8pd/o+0pSonQKUpQApSlAClKUAKUpQApSlAEN2m7OWMZbyXkkjyuPMp9D/TauV8b7O4zA3AfPYGb8S2vUGM43BmNdq7bXkidDqK1OjGrOJW+NobZuljHdd2VIG6XQQw1PiHi+Mp0rc7JY7LbJCls3nEkKxcwZ9JNW7tZ9nuGxStkmw5Myg8BMzLLt8iOdU7E9msbgbT5bffbQySwIkTKjxT+3vV45V6c08PwaaYtR3aIzHNdthw5WVEvb5aRnA+q+laHH7hFllBy6pngCSAgjUnoLX0AqNTE92/e3Ac7EQpESVYHKo5SQJbYAGBUljcXnw8OuV20kLvG+425fI6UznoXi1Rg4RgM5sahUyqWaJjL4Qq+szofU1bbnGUy9xcBC3Axb1tuMs8joOfodqrOGtNat2lIJW04doPmJMqg20EyY6xWot43LoGshWVoEkDMWgE+8aVJlKsi8fw97X3myzZmlGEaB7ZYt3n8p6TUh2GwQDLdYSqsT6FlEKB8walcThxntd5bUqUGVm1nwiY2gE6RJEb1ktXFDLZgKFlreTy5okbRpAK1qaNfVEljeG3LquHJZ1IgnZkMMYnTQyIrDheHqtoLADI/lnU6NMcyQGn2IqYwvG0uI9q4sK7FFgajMuv0JO/0qn9p2ud6qJdDRbC+KQ0qTDabk9aopE+BuLw613xDFGuN48nOJ0gxqND7VJ2rfdXWBt+EzoNRBHP+XpFZOy/AcS5W4LZLxAuXBlReuWdTvvFXPhPYxEcXL7m642GyCd9N2+aV5aY7xJoqfD+AXL138BSlsgZmYeD2PMn2q/8AZzs7awolRmuHzOdz6DoPSpe2gAAAAA2A2r3UpZJS7KQxRh0KUpSFBSlKAFKUoAUpSgBSlKAFKUoAUpSgBSlKAFKUoA0OIcIsXv8AEso56lRP13qu8V+z3DXWDK9y2RsA0r9DVxpQBQOLdgrjgC3iVEbZrfrrsemlQlr7M8UhOS9ZgmTIb+1dapW2ZRyyz9n2MAyG9ZykkmQxmemmhFZ+G/ZlcVy9zFA/pCofDpHM10ylHJmcUU3hvYCxbcXHe5cYEnUgCT6D6VP4DgeHtGUsoG/URLfU61J0otmpJClKVhopSlAClKUAKUpQApSlAClKUAKUpQApSlAClKUAKUpQApSlAClKUAKUpQApSlAClKUAKUpQApSlAClKUAKUpQApSlAClKUAf//Z'

# URL of the image for the node
node_image_url = 'https://www.kingstonpolice.ca/en/services-and-reporting/resources/fingerprints-sm.jpg'

# Custom style for the nodes
node_style = {
    'background': node_color_not_highlighted,
    'border': border_color,
    'highlight': { # style on click
        'background': node_color_highlighted,
        'border': border_color
    }
}

# Instantiate a Network class
graph = Network(
    width='100%', # background width
    height='900px', # background height
    bgcolor=background_color # background color
)

# Add nodes to the graph with various parameters
graph.add_node(
    0, 
    label='Created by:\ncyterat\n\ncircle with\nlink\non hover',
    margin=20, # distance between a node border and label
    title="<a href='https://github.com/cyterat'>https://github.com/cyterat", # hover text
    shape='circle', # node shape (this one allows text inside)
    color=node_style,
    font={
        'color':'black',
        'size': 18,
        'face': 'courier',
        'strokeWidth': 2,
        'strokeColor': 'orange',
    },
    borderWidth=5, # node border width
    size=60, # node size
    shadow=True # node shadow
)
graph.add_node(
    1, 
    label='base64\ncircular\nimage',
    font={
        'background':node_color_highlighted # highlighted text effect
    },
    color=node_style,
    shape='circularImage',
    image=node_image_base64,
    borderWidth=10,
    shadow=True,
    opacity=1
)
graph.add_node(
    2, 
    label="<b><code>base64</code></b> <i>image</i>",
    font={
        'multi': 'html' # enables the use of HTML tags in label
    },
    color=node_style,
    shape='image',
    image=node_image_base64,
    size=50,
    shadow=True
)
graph.add_node(
    3, 
    label='url image',
    color=node_style,
    shape='image',
    image=node_image_url,
    size=40,
    shadow=True
)
graph.add_node(
    4, 
    label='dot shape',
    color=node_style,
    borderWidth=5,
    size=30,
    shadow=True
)
graph.add_node(
    6,
    title="<img src='https://miro.medium.com/v2/resize:fit:/1*4rSaugyj7_jf0uXozP0oxg.gif' width=300 alt='Flowers in Chania'>",
    label="box shape\nwith image\non hover\nmargin=20\nand left align", 
    color=node_style,
    shape='box',
    font={
        'align':'left'
    },
    size=20,
    borderWidth=5,
    margin=20,
    shadow=True
)
graph.add_node(
    7, 
    label='triangle no border', 
    color=node_style,
    shape='triangle',
    borderWidth=0,
    shadow=True
)
graph.add_node(
    8, 
    label='semi-transparent star', 
    color=node_style,
    shape='star',
    shadow=True,
    opacity=0.3,
)

# Add edges (lines) between vertices (nodes)
graph.add_edge(0, 1, width=10, shadow=True)
graph.add_edge(0, 4, width=5, label='top 5.0', font={'align':'top'}, shadow=True)
graph.add_edge(0, 6, width=15, label='middle', font={'color':node_color_highlighted, 'align':'middle', 'strokeWidth': 0}, shadow=True)
graph.add_edge(1,2,shadow=True)
graph.add_edge(1,3,shadow=True)
graph.add_edge(6,7,shadow=True)
graph.add_edge(6,8,shadow=True)

# Set the repulsion (distance) between nodes
graph.repulsion(node_distance=200)

# Save output in an html
graph.show(
    "html/additional-style-franken-graph.html", 
    notebook=False
)

html/additional-style-franken-graph.html

(PyVis) Node Groups¶

In [40]:

# Instantiate a Network class
net = Network()

# Data
data = [
    ('A', 'B', 'anomaly'),
    ('B', 'A', 'anomaly'),
    ('C', 'E', 'normal'),
    ('D', 'C', 'normal'),
    ('E', 'A', 'anomaly')
]

# Set colors for each group
colors = {
    'anomaly': '#e54848',
    'normal': '#333333'
}

# Set fonts for each group
fonts = {
    'anomaly': {
        'color': 'orange',
        'size': 20, 
        'face': 'arial'
    },
    'normal': {
        'color': colors.get('black'),
        'size': 15
    }
}

# Add nodes with color and font based on their group
for source, target, group in data:
    net.add_node(source, color=colors[group], font=fonts[group])
    net.add_node(target, color=colors[group], font=fonts[group])
    net.add_edge(source, target)

# Disable physics
net.toggle_physics(False)

# Show the network
net.show('html/additional-style-groups.html', notebook=False)

html/additional-style-groups.html

pyvis-groups-of-nodes

(PyVis & NetworkX) Circular Graph Layout¶

In [41]:

import networkx as nx
from pyvis.network import Network

# Store graph object
G = nx.karate_club_graph() # NetworkX module example graph

# Overview
print(f"""
NetworkX module example graph:\n
Nodes: {G.nodes}\n
Edges: {G.edges}\n
Degrees: {G.degree}
""")

# Set graph layout
pos = nx.circular_layout(G, scale=500)

# Instantiate a Network class
net = Network()
net.from_nx(G) # convert NetworkX graph into PyVis

# Configure each node
for node in net.get_nodes():
    net.get_node(node)['x'] = pos[node][0]
    net.get_node(node)['y'] = -pos[node][1] #the minus is needed here to respect networkx y-axis convention 
    net.get_node(node)['label'] = str(node) #set the node label as a string so that it can be displayed
    net.get_node(node)['color'] = '#26c8cd'
    net.get_node(node)['size'] = G.degree[node]*2 # set node size equal to its degree x2

# Disable physics (effects on drag)
net.toggle_physics(False)

# Store graph in HTML file and show it
net.show('html/additional-style-circular.html', notebook=False)

NetworkX module example graph:

Nodes: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33]

Edges: [(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8), (0, 10), (0, 11), (0, 12), (0, 13), (0, 17), (0, 19), (0, 21), (0, 31), (1, 2), (1, 3), (1, 7), (1, 13), (1, 17), (1, 19), (1, 21), (1, 30), (2, 3), (2, 7), (2, 8), (2, 9), (2, 13), (2, 27), (2, 28), (2, 32), (3, 7), (3, 12), (3, 13), (4, 6), (4, 10), (5, 6), (5, 10), (5, 16), (6, 16), (8, 30), (8, 32), (8, 33), (9, 33), (13, 33), (14, 32), (14, 33), (15, 32), (15, 33), (18, 32), (18, 33), (19, 33), (20, 32), (20, 33), (22, 32), (22, 33), (23, 25), (23, 27), (23, 29), (23, 32), (23, 33), (24, 25), (24, 27), (24, 31), (25, 31), (26, 29), (26, 33), (27, 33), (28, 31), (28, 33), (29, 32), (29, 33), (30, 32), (30, 33), (31, 32), (31, 33), (32, 33)]

Degrees: [(0, 16), (1, 9), (2, 10), (3, 6), (4, 3), (5, 4), (6, 4), (7, 4), (8, 5), (9, 2), (10, 3), (11, 1), (12, 2), (13, 5), (14, 2), (15, 2), (16, 2), (17, 2), (18, 2), (19, 3), (20, 2), (21, 2), (22, 2), (23, 5), (24, 3), (25, 3), (26, 2), (27, 4), (28, 3), (29, 4), (30, 4), (31, 6), (32, 12), (33, 17)]

html/additional-style-circular.html

pyvis-circular-shape-graph