I. Overview¶
An analysis and regression modeling of over 21,000 real estate transactions in King County, Washington is completed to improve home valuation and real estate advisory. The findings include top features that are important to the bestimate model, which are square footage of living space, distance to Seattle, total distance to both Seattle and Redmond, distance to Redmond, and square footage of living space of the nearest 15 neighbors. The bestimate model that is the tuned random forest performs best in predicting house prices based on over 20 features. It explains 88% of the variance in the data and its predictions are USD 107,000 off from the actual prices on average.
II. Business Problem¶
Real estate agencies in King County, Washington may be able to improve their advisory services by identifying important features that factor in home valuation based on relevant data. Doing so will allow real estate agents to provide more accurate prices to clients as supported by historical records. Using publicly available data, I describe patterns in real estate transactions such as features that likely drive prices. To take it a step further, I develop a prototype for a client-facing application that serves as a home value estimator, modeled from the data.
III. Data Understanding¶
The King County data spans a year between 2014 and 2015 with over 21,000 real estate transactions. Among the 21 variables featured, price is the dependent variable to predict. A full description of all column features is provided along with other data files, available in the repository's data folder.
To prepare the data for analysis, the pre-processing steps are taken below:
- Convert
dateto a date time format and createmonthfeature - Remove outliers for
priceandbedrooms - Replace values for
waterfront,view,condition,gradewith a number scale for consistency - Create
basementfeature usingsqft_basementto determine basement or none - Create
renovatedfeature usingyr_renovatedto determine renovation or none - Create
agefeature by subtracting theyr_builtfrom year ofdatesold
import pandas as pd
import numpy as np
# Import the dataset
data = pd.read_csv('data/kc_house_data.csv')
pd.set_option('display.max_columns', 30)
# Quick look at the data structure
data.head(3)
| id | date | price | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7129300520 | 10/13/2014 | 221900.0 | 3 | 1.00 | 1180 | 5650 | 1.0 | NaN | NONE | Average | 7 Average | 1180 | 0.0 | 1955 | 0.0 | 98178 | 47.5112 | -122.257 | 1340 | 5650 |
| 1 | 6414100192 | 12/9/2014 | 538000.0 | 3 | 2.25 | 2570 | 7242 | 2.0 | NO | NONE | Average | 7 Average | 2170 | 400.0 | 1951 | 1991.0 | 98125 | 47.7210 | -122.319 | 1690 | 7639 |
| 2 | 5631500400 | 2/25/2015 | 180000.0 | 2 | 1.00 | 770 | 10000 | 1.0 | NO | NONE | Average | 6 Low Average | 770 | 0.0 | 1933 | NaN | 98028 | 47.7379 | -122.233 | 2720 | 8062 |
# Convert date to date time format
data['date'] = pd.to_datetime(data['date'])
data['month'] = pd.DatetimeIndex(data['date']).month
Summary statistics of numerical features:
data.drop(columns=['id', 'zipcode', 'lat', 'long']).describe().T.astype('int')
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| price | 21597 | 540296 | 367368 | 78000 | 322000 | 450000 | 645000 | 7700000 |
| bedrooms | 21597 | 3 | 0 | 1 | 3 | 3 | 4 | 33 |
| bathrooms | 21597 | 2 | 0 | 0 | 1 | 2 | 2 | 8 |
| sqft_living | 21597 | 2080 | 918 | 370 | 1430 | 1910 | 2550 | 13540 |
| sqft_lot | 21597 | 15099 | 41412 | 520 | 5040 | 7618 | 10685 | 1651359 |
| floors | 21597 | 1 | 0 | 1 | 1 | 1 | 2 | 3 |
| sqft_above | 21597 | 1788 | 827 | 370 | 1190 | 1560 | 2210 | 9410 |
| yr_built | 21597 | 1970 | 29 | 1900 | 1951 | 1975 | 1997 | 2015 |
| yr_renovated | 17755 | 83 | 399 | 0 | 0 | 0 | 0 | 2015 |
| sqft_living15 | 21597 | 1986 | 685 | 399 | 1490 | 1840 | 2360 | 6210 |
| sqft_lot15 | 21597 | 12758 | 27274 | 651 | 5100 | 7620 | 10083 | 871200 |
| month | 21597 | 6 | 3 | 1 | 4 | 6 | 9 | 12 |
Data Cleaning
import matplotlib.pyplot as plt
import seaborn as sns
# Create dataframe with price in millions
price_data = data[['price']]/1000000
plt.figure(figsize=(12, 2))
plt.style.use('bmh')
sns.boxplot(x='price', data=price_data, color='teal')
plt.title('Distribution of Prices (USD Million)')
plt.savefig('data/images/fig0.png', dpi=200, transparent=True)
plt.show()
# Remove outliers in prices
data = data[(data.price < data.price.quantile(.995)) &
(data.price > data.price.quantile(.005))]
plt.figure(figsize=(8, 2))
sns.boxplot(x='bedrooms', data=data, color='honeydew')
plt.title('Distribution of Bedrooms')
plt.savefig('data/images/fig1.png', dpi=200, transparent=True)
plt.show()
Likely a typographical error, the number of 33 bedrooms is corrected to 3.
data.loc[(data.bedrooms == 33), 'bedrooms'] = 3
# Replace missing values with no waterfront
data.loc[data['waterfront'].isnull(), 'waterfront'] = 'NO'
data['waterfront'] = data['waterfront'].apply(lambda x: 0 if x == 'NO' else 1)
# Replace missing values with no view
data.loc[data.view.isnull(), 'view'] = 'NONE'
data['view'] = data['view'].replace({'NONE':0,
'FAIR':1,
'AVERAGE':2,
'GOOD':3,
'EXCELLENT':4})
data['condition'] = data['condition'].replace({'Poor':0,
'Fair':1,
'Average':2,
'Good':3,
'Very Good':4})
data['grade'] = data['grade'].map(lambda x: int(x.split(' ')[0])) # only keep the number from string
# Replace missing values with 0 square footage of basement
data['sqft_basement'] = data['sqft_basement'].replace('?', '0').astype('float')
data['basement'] = data['sqft_basement'].apply(lambda x: 0 if x == 0 else 1)
# Replace missing values with not renovated
data.loc[data['yr_renovated'].isnull(), 'yr_renovated'] = 0
data['renovated'] = data['yr_renovated'].apply(lambda x: 0 if x == 0 else 1)
data['age'] = data['date'].dt.year - data['yr_built']
3.1 Exploratory Data Analysis¶
Month-over-month comparison:
date_data = data[['date', 'price']]
date_data = data.set_index('date', drop=True).astype('float64')
# Resample data to count transactions per month
monthly_count = date_data.resample('MS').count()
monthly_count = monthly_count.drop(monthly_count.index[-1])
# Resample data to calculate mean price per month
monthly_avg = date_data.resample('MS').mean()
monthly_avg = monthly_avg.drop(monthly_avg.index[-1])
fig, axes = plt.subplots(ncols=2, figsize=(12,4))
monthly_count['price'].plot(title='Total Count', ax=axes[0], colormap='Set3', marker='.')
monthly_avg['price'].plot(title='Average Price', ax=axes[1], colormap='BrBG_r', marker='.')
axes[0].grid(axis='x', linewidth=0)
axes[1].grid(axis='x', linewidth=0)
plt.suptitle('Houses Sold Per Month', fontsize=14)
plt.savefig('data/images/fig2.png', dpi=200, transparent=True)
plt.show()
The highest peaks in the number of houses sold per month happened in the seasons of spring and summer. The decline in the months that followed dropped to the lowest point at the first month of the new year. As for the price of houses sold per month, the values followed roughly the same pattern.
Check for multicollinearity:
def check_correlation(data, threshold):
'''Checks for the highest correlated features in a dataframe given a threshold'''
df = data.corr().abs().stack().reset_index().sort_values(0, ascending=False)
df['pairs'] = list(zip(df['level_0'], df['level_1']))
df = df.set_index(['pairs']).drop(columns=['level_1', 'level_0'])
df.columns = ['correlation']
df = df.drop_duplicates()
df = df[(df['correlation'] > threshold) & (df['correlation'] < 1)]
return df
check_correlation(data, 0.75)
| correlation | |
|---|---|
| pairs | |
| (yr_renovated, renovated) | 0.999968 |
| (age, yr_built) | 0.999873 |
| (sqft_living, sqft_above) | 0.869907 |
| (basement, sqft_basement) | 0.826651 |
| (sqft_living15, sqft_living) | 0.753874 |
| (sqft_living, grade) | 0.751196 |
# Drop highly collinear features and useless feature like id
to_drop = ['id', 'date', 'yr_renovated', 'sqft_above', 'sqft_basement', 'yr_built', 'yr_renovated']
data = data.drop(columns=to_drop)
plt.figure(figsize=(10,8))
plt.style.use('default')
corr = data.corr()
mask = np.triu(np.ones_like(corr, dtype=bool))
sns.heatmap(corr.abs(), mask=mask, cmap='YlGnBu')
plt.title('Feature Correlation with Price', fontsize=14)
plt.savefig('data/images/fig3.png', dpi=200, transparent=True)
plt.show()
Price is strongly correlated with sqft_living, grade, sqft_living15, bathrooms, and bathrooms.
Let's visualize their relationships and distributions.
select_features = ['price', 'bathrooms', 'sqft_living', 'grade']
sns.pairplot(data, vars=select_features, diag_kind='kde', corner=True).fig.suptitle('Relationships between Price and Select Features',
fontsize=16, y=1)
plt.savefig('data/images/fig4.png', dpi=200, transparent=True)
plt.show()
3.2 Geospatial Mapping¶
'Location, location, location'
Location is important in real estate and in analysis!
Let's map the data points.
import geopandas as gpd
from shapely.geometry import Point, Polygon
def map_data(data_, title, name, colormap):
'''Plots the data points using latitude and longitude on top of King County map'''
plt.style.use('seaborn')
fig, ax = plt.subplots(figsize=(8,8))
king_county_fig = gpd.read_file('data/map/Incorporated_Areas_of_King_County___city_area.shp')
geometry = [Point(xy) for xy in zip(data_['long'], data_['lat'])]
geo_data = gpd.GeoDataFrame(data_, crs='EPSG:4326', geometry=geometry)
king_county_fig.plot(ax=ax, alpha=0.4, color='grey')
geo_data.plot(column='price', ax=ax, alpha=0.4, legend=True, markersize=8, cmap=plt.get_cmap(colormap), legend_kwds={'shrink': 0.7, 'format': '%.0f'})
plt.xlim(data['long'].min(), data['long'].max())
plt.ylim(data['lat'].min(), data['lat'].max())
plt.ticklabel_format(style='plain')
plt.title(title, fontsize=14)
plt.savefig(f'data/images/{name}.png', dpi=200, transparent=True)
plt.show()
# Create dataframe of houses sold under a million dollars
UnderMillion = data.loc[(data['price'] < 1000000)]
# Create dataframe of houses sold over a million dollars
OverMillion = data.loc[(data['price'] >= 1000000)]
# Store dataframe for retrieval in map notebook
%store UnderMillion
Stored 'UnderMillion' (DataFrame)
# Store dataframe for retrieval in map notebook
%store OverMillion
Stored 'OverMillion' (DataFrame)
map_data(UnderMillion, 'House Prices Sold Under $1 Million', 'fig5', 'PuBuGn')
The concentrated geographic patterns reveal parts of the county populated by the more expensive houses represented by darker colors like the island at the center. The even more expensive houses sold for over a million dollars are located at about the same spots as the dark dots.
Locate the highest priced houses in the data in the following map:
map_data(OverMillion, 'House Prices Sold Over $1 Million', 'fig6', 'Greens')
Interactive Map
I created choropleth maps (map notebook) to further understand how house prices vary by location.
To interact with the maps, please use the notebook viewer.
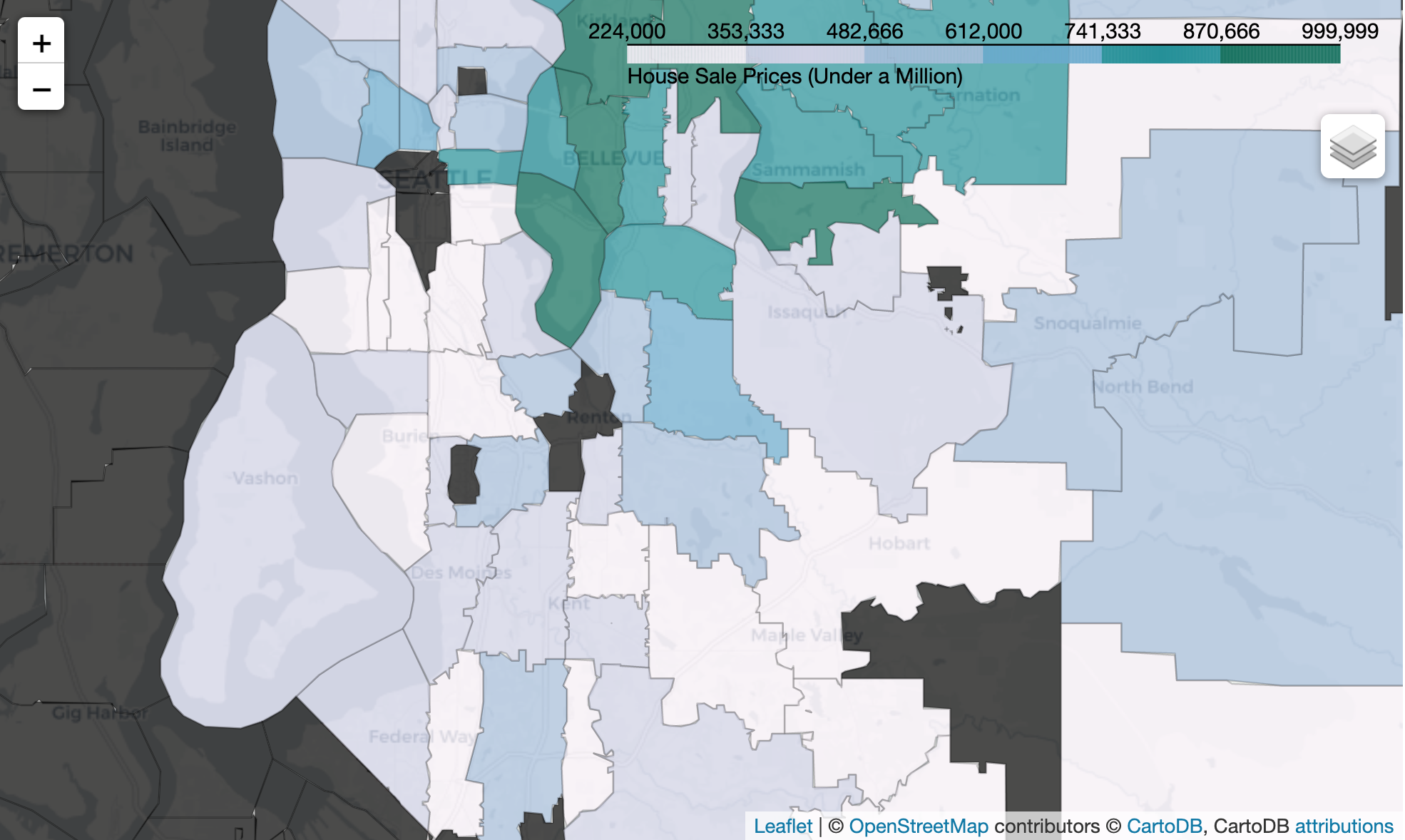
3.3 Feature Engineering¶
King County Population:
# Import data from population census
population = pd.read_csv('data/population.csv')
population_density = population.loc[:, ['City Name', 'Total Population 2010', 'Population Density (Persons / Square Mile) 2010']]
population_density = population_density.rename(columns={'City Name':'city', 'Total Population 2010':'population', 'Population Density (Persons / Square Mile) 2010':'pop_density'})
king_county_cities = ['Algona', 'Auburn', 'Beaux Arts Village', 'Bellevue', 'Black Diamond',
'Bothell', 'Burien', 'Carnation', 'Clyde Hill', 'Covington',
'Des Moines', 'Duvall', 'Enumclaw', 'Federal Way', 'Hunts Point',
'Issaquah', 'Kenmore', 'Kent', 'Kirkland', 'Lake Forest Park',
'Maple Valley', 'Medina', 'Mercer Island', 'Milton', 'Newcastle',
'Normandy Park', 'North Bend', 'Pacific', 'Redmond', 'Renton',
'Sammamish', 'SeaTac', 'Seattle', 'Shoreline', 'Skykomish',
'Snoqualmie', 'Tukwila', 'Woodinville', 'Yarrow Point']
city_names = pd.DataFrame(king_county_cities, columns=['city'])
import warnings
warnings.filterwarnings('ignore')
king_county_population = pd.merge(population_density, city_names, on=['city'])
king_county_population = king_county_population.append({'city':'Vashon','population':10624, 'pop_density':287.22}, ignore_index=True)
zipcodes = pd.read_csv('data/zipcodes.csv')
zipcodes['city'] = zipcodes['zipcode'].apply(lambda x: x.split('(')[1].strip('()'))
zipcodes['zipcode'] = zipcodes['zipcode'].apply(lambda x: int(x.split()[0]))
# Map population data to cities
king_county_zipcode = pd.merge(king_county_population, zipcodes, on=['city'])
engineered_data = pd.merge(data, king_county_zipcode, how='inner', on=['zipcode'])
Distance to Seattle and Redmond:
from haversine import haversine, Unit
def find_distance(center, lat, long):
'''Uses haversine function to find distance between a given center and a point's latitude and longitude'''
house = (lat, long)
distance = haversine(center, house, unit=Unit.MILES)
return distance
def add_distance(data):
'''Applies the find_distance function to dataframe to add columns for distances to Seattle and Redmond'''
seattle = (47.608013, -122.335167)
redmond = (47.673988, -122.121513)
data['to_seattle'] = data.apply(lambda x: find_distance(seattle, x['lat'], x['long']), axis=1)
data['to_redmond'] = data.apply(lambda x: find_distance(redmond, x['lat'], x['long']), axis=1)
data['distance'] = data['to_seattle'] + data['to_redmond']
data = data.drop(columns=['lat', 'long'])
return data
engineered_data = add_distance(engineered_data)
IV. Data Modeling¶
Train Test Split
from sklearn.model_selection import train_test_split
X = data.drop(columns=['price'])
y = data['price']
X_tr, X_te, y_tr, y_te = train_test_split(X, y, random_state=112221)
Baseline Model:
# Simple linear regression using one independent variable
from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()
lr_model.fit(X_tr[['sqft_living']], y_tr)
baseline_pred = lr_model.predict(X_te[['sqft_living']])
# Evaluate using R squared and RMSE scores
from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_squared_error
baseline_cross_val = cross_val_score(lr_model, X_tr[['sqft_living']], y_tr, scoring='neg_root_mean_squared_error', cv=10)
baseline_cross_val_mean = -(baseline_cross_val.mean())
baseline_rmse = mean_squared_error(y_te, baseline_pred, squared=False)
baseline_score = lr_model.score(X_te[['sqft_living']], y_te)
metric_table = pd.DataFrame(columns = ['model', 'cv_rmse', 'test_rmse', 'test_score'])
metric_table = metric_table.append({'model': 'simple_lr',
'cv_rmse': f'{baseline_cross_val_mean:.2f}',
'test_rmse': f'{baseline_rmse:.2f}',
'test_score': f'{baseline_score:.2f}'}, ignore_index=True)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
4.1 Linear Regression¶
Multiple Linear Regression:
def run_model(regressor, name, X_train=X_tr, X_test=X_te, y_train=y_tr, y_test=y_te):
'''Fits a regression model on train set, predicts on the test set, and returns cross validation and test scores'''
regressor.fit(X_train, y_train)
y_pred = regressor.predict(X_test)
cross_val = cross_val_score(regressor, X_train, y_train, scoring='neg_root_mean_squared_error', cv=10)
cross_val_mean = -(cross_val.mean())
rmse = mean_squared_error(y_test, y_pred, squared=False)
score = regressor.score(X_test, y_test)
return metric_table.append({'model': name,
'cv_rmse': f'{cross_val_mean:.2f}',
'test_rmse': f'{rmse:.2f}',
'test_score': f'{score:.2f}'}, ignore_index=True)
# Use multiple numerical features
num_feat = ['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floors', 'sqft_living15', 'sqft_lot15', 'age']
metric_table = run_model(lr_model, 'multiple_lr', X_tr[num_feat], X_te[num_feat])
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
Standardization:
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_sc_tr = pd.DataFrame(scaler.fit_transform(X_tr[num_feat], y_tr), columns=X_tr[num_feat].columns, index=X_tr[num_feat].index)
X_sc_te = pd.DataFrame(scaler.transform(X_te[num_feat]), columns=X_te[num_feat].columns, index=X_te[num_feat].index)
metric_table = run_model(lr_model, 'standardized_lr', X_sc_tr, X_sc_te)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
# Data with engineered features such as population and distance
X_ = engineered_data.drop(columns=['price'])
y_ = engineered_data['price']
X_train, X_test, y_train, y_test = train_test_split(X_, y_, random_state=112221)
# Store for retrieval in grid search notebook
%store X_train
Stored 'X_train' (DataFrame)
# Store for retrieval in grid search notebook
%store y_train
Stored 'y_train' (Series)
num_feat.extend(['population', 'pop_density', 'to_seattle', 'to_redmond', 'distance'])
X_scaled_train = pd.DataFrame(scaler.fit_transform(X_train[num_feat], y_train), columns=X_train[num_feat].columns, index=X_train[num_feat].index)
X_scaled_test = pd.DataFrame(scaler.transform(X_test[num_feat]), columns=X_test[num_feat].columns, index=X_test[num_feat].index)
metric_table = run_model(lr_model, 'feature_lr', X_scaled_train, X_scaled_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
Machine Learning Pipeline:
from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder
num_pipe = Pipeline(steps=[
('num_imputer', SimpleImputer(strategy='median')),
('scaler', StandardScaler())
])
# Perform one hot encoding on categorical features
cat_pipe = Pipeline(steps=[
('cat_imputer', SimpleImputer(strategy='most_frequent')),
('ohe', OneHotEncoder(handle_unknown='ignore'))
])
from sklearn.compose import ColumnTransformer
num_features = ['bedrooms', 'bathrooms', 'sqft_living', 'sqft_lot', 'floors', 'sqft_living15', 'sqft_lot15',
'age', 'population', 'pop_density', 'to_seattle', 'to_redmond', 'distance']
cat_features = ['waterfront', 'view', 'condition', 'grade', 'zipcode', 'month', 'basement', 'renovated', 'city']
col_transformer = ColumnTransformer([
('num_transformer', num_pipe, num_features),
('cat_transformer', cat_pipe, cat_features)
])
# Multiple linear regression using all features
lr_pipe = Pipeline(steps=[
('col_transformer', col_transformer),
('lr', LinearRegression())
])
metric_table = run_model(lr_pipe, 'pipeline_lr', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
Ridge and Lasso Regression:
from sklearn.linear_model import Ridge
ridge_pipe = Pipeline(steps=[
('col_transformer', col_transformer),
('ridge', Ridge())
])
metric_table = run_model(ridge_pipe, 'ridge_lr', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
| 5 | ridge_lr | 124635.57 | 119894.29 | 0.85 |
from sklearn.linear_model import Lasso
lasso_pipe = Pipeline(steps=[
('col_transformer', col_transformer),
('lasso', Lasso(max_iter=2000))
])
metric_table = run_model(lasso_pipe, 'lasso_lr', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
| 5 | ridge_lr | 124635.57 | 119894.29 | 0.85 |
| 6 | lasso_lr | 124231.29 | 119121.01 | 0.85 |
Polynomial Regression:
from sklearn.preprocessing import PolynomialFeatures
poly_col_transformer = ColumnTransformer([
('num_transformer', num_pipe, num_features),
('polynomial', PolynomialFeatures(2), num_features),
('cat_transformer', cat_pipe, cat_features),
])
poly_pipe = Pipeline(steps=[
('poly_col_transformer', poly_col_transformer),
('lr', LinearRegression())
])
metric_table = run_model(poly_pipe, 'poly_lr', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
| 5 | ridge_lr | 124635.57 | 119894.29 | 0.85 |
| 6 | lasso_lr | 124231.29 | 119121.01 | 0.85 |
| 7 | poly_lr | 112687.15 | 110277.17 | 0.87 |
4.2 Decision Tree¶
from sklearn.tree import DecisionTreeRegressor
dt_pipe = Pipeline(steps=[
('col_transformer', col_transformer),
('decision_tree', DecisionTreeRegressor())
])
metric_table = run_model(dt_pipe, 'default_dt', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
| 5 | ridge_lr | 124635.57 | 119894.29 | 0.85 |
| 6 | lasso_lr | 124231.29 | 119121.01 | 0.85 |
| 7 | poly_lr | 112687.15 | 110277.17 | 0.87 |
| 8 | default_dt | 165174.85 | 162057.54 | 0.72 |
# Store for retrieval in grid search notebook
%store dt_pipe
Stored 'dt_pipe' (Pipeline)
poly_dt = Pipeline(steps=[
('poly_col_transformer', poly_col_transformer),
('decision_tree', DecisionTreeRegressor())
])
metric_table = run_model(poly_dt, 'poly_dt', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
| 5 | ridge_lr | 124635.57 | 119894.29 | 0.85 |
| 6 | lasso_lr | 124231.29 | 119121.01 | 0.85 |
| 7 | poly_lr | 112687.15 | 110277.17 | 0.87 |
| 8 | default_dt | 165174.85 | 162057.54 | 0.72 |
| 9 | poly_dt | 170853.84 | 163749.93 | 0.71 |
Grid search (notebook) is performed to find the optimal parameters of the Decision Tree model.
tuned_dt = Pipeline(steps=[
('col_transformer', col_transformer),
('decision_tree', DecisionTreeRegressor(criterion='friedman_mse', max_depth=None, min_samples_leaf=5, min_samples_split=45))
])
metric_table = run_model(tuned_dt, 'tuned_dt', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
| 5 | ridge_lr | 124635.57 | 119894.29 | 0.85 |
| 6 | lasso_lr | 124231.29 | 119121.01 | 0.85 |
| 7 | poly_lr | 112687.15 | 110277.17 | 0.87 |
| 8 | default_dt | 165174.85 | 162057.54 | 0.72 |
| 9 | poly_dt | 170853.84 | 163749.93 | 0.71 |
| 10 | tuned_dt | 142144.75 | 138223.89 | 0.80 |
poly_tuned_dt = Pipeline(steps=[
('poly_col_transformer', poly_col_transformer),
('decision_tree', DecisionTreeRegressor(criterion='friedman_mse', max_depth=None, min_samples_leaf=5, min_samples_split=45))
])
metric_table = run_model(poly_tuned_dt, 'poly_tuned_dt', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
| 5 | ridge_lr | 124635.57 | 119894.29 | 0.85 |
| 6 | lasso_lr | 124231.29 | 119121.01 | 0.85 |
| 7 | poly_lr | 112687.15 | 110277.17 | 0.87 |
| 8 | default_dt | 165174.85 | 162057.54 | 0.72 |
| 9 | poly_dt | 170853.84 | 163749.93 | 0.71 |
| 10 | tuned_dt | 142144.75 | 138223.89 | 0.80 |
| 11 | poly_tuned_dt | 147828.92 | 137763.62 | 0.80 |
4.3 Random Forest¶
from sklearn.ensemble import RandomForestRegressor
rf_pipe = Pipeline(steps=[
('col_transformer', col_transformer),
('random_forest', RandomForestRegressor())
])
metric_table = run_model(rf_pipe, 'default_rf', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
| 5 | ridge_lr | 124635.57 | 119894.29 | 0.85 |
| 6 | lasso_lr | 124231.29 | 119121.01 | 0.85 |
| 7 | poly_lr | 112687.15 | 110277.17 | 0.87 |
| 8 | default_dt | 165174.85 | 162057.54 | 0.72 |
| 9 | poly_dt | 170853.84 | 163749.93 | 0.71 |
| 10 | tuned_dt | 142144.75 | 138223.89 | 0.80 |
| 11 | poly_tuned_dt | 147828.92 | 137763.62 | 0.80 |
| 12 | default_rf | 113631.61 | 106799.75 | 0.88 |
# Store for retrieval in grid search notebook
%store rf_pipe
Stored 'rf_pipe' (Pipeline)
Grid search (notebook) is performed to find the optimal parameters of the Random Forest model.
tuned_rf = Pipeline(steps=[
('col_transformer', col_transformer),
('random_forest', RandomForestRegressor(criterion='friedman_mse', max_depth=None, min_samples_leaf=1, min_samples_split=2, n_estimators=150))
])
metric_table = run_model(tuned_rf, 'tuned_rf', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
| 5 | ridge_lr | 124635.57 | 119894.29 | 0.85 |
| 6 | lasso_lr | 124231.29 | 119121.01 | 0.85 |
| 7 | poly_lr | 112687.15 | 110277.17 | 0.87 |
| 8 | default_dt | 165174.85 | 162057.54 | 0.72 |
| 9 | poly_dt | 170853.84 | 163749.93 | 0.71 |
| 10 | tuned_dt | 142144.75 | 138223.89 | 0.80 |
| 11 | poly_tuned_dt | 147828.92 | 137763.62 | 0.80 |
| 12 | default_rf | 113631.61 | 106799.75 | 0.88 |
| 13 | tuned_rf | 113358.20 | 106711.56 | 0.88 |
poly_tuned_rf = Pipeline(steps=[
('poly_col_transformer', poly_col_transformer),
('random_forest', RandomForestRegressor(criterion='friedman_mse', max_depth=None, min_samples_leaf=1, min_samples_split=2, n_estimators=150))
])
metric_table = run_model(poly_tuned_rf, 'poly_tuned_rf', X_train, X_test, y_train, y_test)
metric_table
| model | cv_rmse | test_rmse | test_score | |
|---|---|---|---|---|
| 0 | simple_lr | 227585.85 | 217065.62 | 0.47 |
| 1 | multiple_lr | 206288.15 | 198811.78 | 0.56 |
| 2 | standardized_lr | 206288.15 | 198811.78 | 0.56 |
| 3 | feature_lr | 177887.09 | 173055.45 | 0.68 |
| 4 | pipeline_lr | 124231.74 | 119145.65 | 0.85 |
| 5 | ridge_lr | 124635.57 | 119894.29 | 0.85 |
| 6 | lasso_lr | 124231.29 | 119121.01 | 0.85 |
| 7 | poly_lr | 112687.15 | 110277.17 | 0.87 |
| 8 | default_dt | 165174.85 | 162057.54 | 0.72 |
| 9 | poly_dt | 170853.84 | 163749.93 | 0.71 |
| 10 | tuned_dt | 142144.75 | 138223.89 | 0.80 |
| 11 | poly_tuned_dt | 147828.92 | 137763.62 | 0.80 |
| 12 | default_rf | 113631.61 | 106799.75 | 0.88 |
| 13 | tuned_rf | 113358.20 | 106711.56 | 0.88 |
| 14 | poly_tuned_rf | 115789.84 | 107797.20 | 0.88 |
# The best model with the best estimate
bestimate_model = tuned_rf
bestimate_model.fit(X_train, y_train)
bestimate_pred = bestimate_model.predict(X_test)
V. Results¶
Model Performance:
# Visualize the metrics evaluated per model
metric_table[['cv_rmse', 'test_rmse', 'test_score']] = metric_table[['cv_rmse', 'test_rmse', 'test_score']].astype('float')
plt.style.use('bmh')
fig, axes = plt.subplots(nrows=2, figsize=(18,12))
# First metric is the R-squared score
sns.barplot(x='model', y='test_score', data=metric_table, palette='BuPu', ax=axes[0], zorder=99)
axes[0].set_xlabel('')
axes[0].set_ylabel('R²')
axes[0].set_ylim(0, 1)
axes[0].set_title('Comparison of Model Performance: R²')
# Second metric is the root mean squared error
sns.barplot(x='model', y='test_rmse', data=metric_table, palette='BuPu', ax=axes[1], zorder=99)
axes[1].set_xlabel('')
axes[1].set_ylabel('RMSE')
axes[1].set_title('Comparison of Model Performance: Root Mean Squared Error')
plt.savefig('data/images/fig8.png', dpi=200, transparent=True)
plt.show()
Baseline to Bestimate Model
The baseline model simple_lr significantly improved to the tuned_rf, our bestimate model:
- from an R-squared of 0.47 to 0.88, and
- from a Root Mean Squared Error of USD 217,000 to USD 107,000
To visualize the significant difference, let's plot how far away the predictions of the baseline model are to the actual prices versus how much closer the predictions of the bestimate model are:
plt.style.use('default')
fig, axes = plt.subplots(ncols=2, figsize=(12,6))
# Perfect line where the predicted price is equal to the actual price
perfect_line = np.arange(0, 3)
# Baseline simple linear regression model
axes[0].plot(perfect_line, linestyle='--', color='black', label='prediction value')
axes[0].scatter(y_test/1000000, baseline_pred/1000000, alpha=0.1, color='cornflowerblue', label='price')
axes[0].set_xlabel('Predicted Price in Millions')
axes[0].set_ylabel('Actual Price in Millions')
axes[0].set_title('Baseline Model \n R²: 47% RMSE: $217,000')
axes[0].set_xlim(0, 2)
axes[0].set_ylim(0, 2)
axes[0].legend()
# Bestimate random forest model
axes[1].plot(perfect_line, linestyle='--', color='black', label='prediction value')
axes[1].scatter(y_test/1000000, bestimate_pred/1000000, alpha=0.1, color='plum', label='price')
axes[1].set_xlabel('Predicted Price in Millions')
axes[1].set_ylabel('Actual Price in Millions')
axes[1].set_title('Bestimate Model \n R²: 88% RMSE: $107,000')
axes[1].set_xlim(0, 2)
axes[1].set_ylim(0, 2)
axes[1].legend()
plt.savefig('data/images/fig9.png', dpi=200, transparent=True)
plt.show()
Important features under the bestimate model:
from sklearn.inspection import permutation_importance
result = permutation_importance(bestimate_model, X_test, y_test, n_repeats=10, random_state=112221, n_jobs=2)
sorted_idx = result.importances_mean.argsort()
plt.style.use('bmh')
fig, ax = plt.subplots(figsize=(16,12))
ax.boxplot(result.importances[sorted_idx].T, vert=False, labels=X_test.columns[sorted_idx], )
ax.set_title('Permutation Importances', fontsize=16)
ax.set_xlabel('Mean of Feature Importance')
ax.set_ylabel('Feature')
plt.savefig('data/images/fig10.png', dpi=200, transparent=True)
plt.show()
For advisory, the top five features with the highest mean feature importances to the model are:
- Square footage of living space
- Distance to Seattle
- Total distance to both Seattle and Redmond
- Distance to Redmond
- Square footage of living space of the nearest 15 neighbors
The other important features that follows are overall grade related to the construction and design of the house, quality of view from the house, zipcode, whether the house is on a waterfront, and square footage of lot.
Model Deployment
Finally, I deploy the Random Forest regression model (demo) as a prototype I develop for a client-facing application that serves as a Home Value Estimator.
VI. Further Research¶
For further research, the data should be updated to more recent transactions in King County, and more features should be added such as more information on comparable and neighboring houses.