Musculoskeletal modeling and simulation¶
Marcos Duarte, Renato Watanabe
Laboratory of Biomechanics and Motor Control
Federal University of ABC, Brazil
We will now simulate the dynamics of the musculoskeletal system with muscle dynamics.
You should have read Muscle modeling and Muscle simulation.
In addition, chapter 4 of Nigg and Herzog (2006) is a good introduction to this topic.
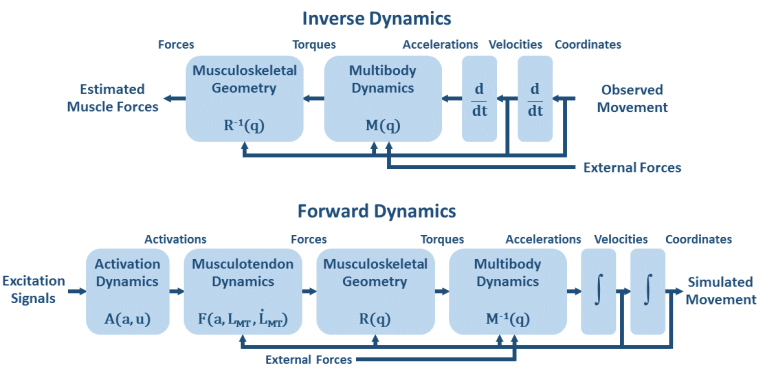
Forward and inverse dynamics¶
In a typical movement analysis using inverse dynamics, we would measure the leg and thigh positions, calculate the leg and knee linear and angular position and acceleration, and then estimate the net moment of force at the knee joint and force of the quadriceps muscle using the equation above. Now, we want to perform forward dynamics, i.e., muscle force will be the input and the movement of the leg will be the output. The figure below compares the forward (direct) and inverse dynamics approaches.
One-link system with one DoF and one muscle¶
Let's start with the simplest case, a one-link rigid body with one degree of freedom and one muscle.
Let's simulate the extension movement of the knee. This problem is based on an example from chapter 4 of Nigg and Herzog (2006). We will model the task as a planar movement, the leg and foot as one rigid segment and the rest of the body fixed, the knee as a revolute joint with fixed axis of rotation and one degree of freedom, and only one muscle as knee extensor, as illustrated in the figure below.
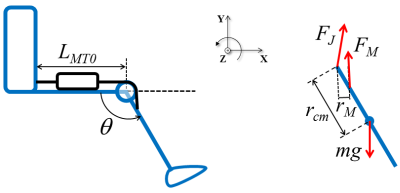
Where $I$ is the rotational inertia of the leg+foot segment around the knee joint.
In our convention, the first term on the left-hand side is a positive (extensor) moment of force and the second term is a negative (flexor) moment of force when $\theta$ is greater than $90^o$. The Newton-Euler equation above is a second-order nonlinear differential equation.
The dependence of the length of the quadriceps muscle-tendon unit with the knee angle is given by:
$$ L_{MT} = L_{MT0} - r_m (\theta - \pi/2) $$Examining the equations above, if we excite the muscle, it will generate force which will be transmitted to the leg segment and accelerate it, which in turn will vary the muscle length and velocity, affecting the muscle force. We already have seen that muscle force is related to muscle length and velocity by a first-order ODE (see Muscle simulation). So, muscle force and joint angle are described by two coupled ODEs. Mathematically, this means that the musculoskeletal system we modeled has as state variables: $L_M$, $\dot{L}_M$, and $\theta$ (and muscle activation $a$ could also be considered as a state variable in certain situations, but not for the present problem, where we consider it as an input parameter). Let's rewrite the Newton-Euler equation in a more clear form:
$$ \frac{\mathrm{d}^2 \theta}{\mathrm{d}t^2} = I^{-1} \left[ r_M F_M + r_{cm}\cos(\theta)mg \right] $$$F_M$ will be determined when $L_M$ is calculated, which according to the muscle model we used in Muscle simulation is the solution of the following first-order ODE:
$$ \frac{\mathrm{d} L_M}{\mathrm{d}t} = f_v^{-1}\left(\frac{F_{SE}(L_{MT}-L_M\cos\alpha)/\cos\alpha - F_{PE}(L_M)}{a f_l(L_M)}\right) $$And:
$$ F_M = F_{SE}(L_{MT}-L_M\cos\alpha)/\cos\alpha $$To apply numerical methods to solve these coupled equations, we have to express them as a system of first-order differential equations (see Ordinary differential equation):
$$ \left\{ \begin{array}{l l} \frac{\mathrm{d} L_M}{\mathrm{d}t} = & f^{-1}_{v}(L_M(\theta)), \quad &L_M(t_0) = L_{M0} \\ \frac{\mathrm{d} \theta}{\mathrm{d}t} = &\omega, \quad &\theta(t_0) = \theta \\ \frac{\mathrm{d} \omega}{\mathrm{d}t} = &I^{-1} \left[ r_M F_M(L_M(\theta)) + r_{cm}\cos(\theta)mg \right], \quad &\omega(t_0) = \omega_0 \end{array} \right.$$Let's solve this problem in Python.
First, let's import the necessary Python libraries and customize the environment:
import numpy as np
%matplotlib notebook
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['lines.linewidth'] = 2
matplotlib.rcParams['font.size'] = 12
matplotlib.rcParams['lines.markersize'] = 4
matplotlib.rc('axes', grid=True, labelsize=12, titlesize=13, ymargin=0.01)
matplotlib.rc('legend', numpoints=1, fontsize=10)
from scipy.integrate import odeint, ode
# import the muscles.py module
import sys
sys.path.insert(1, r'./../functions')
import muscles
Let's define a function with the system of first-order ODEs:
def onelink_eq(lmthetaomega, t):
"""equation for one-link system."""
# parameters from Nigg and Herzog (2006)
lmt0 = 0.310
rm = 0.033
rcm = 0.264
m = 10
g = 9.8
I = 0.1832
lm = lmthetaomega[0] # muscle length
theta = lmthetaomega[1] # knee position
omega = lmthetaomega[2] # knee velocity
lmt = lmt0 - rm_fun(theta)*(theta - np.pi/2)
lmd = fv_1_eq(t, lm, lmt)
thetadd = (rm_fun(theta)*fm_eq(lm, lmd, lmt) + rcm*np.cos(theta)*m*g)/I # acceleration
return [lmd, omega, thetadd]
# define a function for the moment arm
def rm_fun(theta):
"""Vastus intermedius moment arm."""
rm = 0.033
return rm
Functions to calculate the force-velocity relationship:
def fv_1_eq(t, lm, lmt):
lmopt = ms.P['lmopt']
ltslack = ms.P['ltslack']
a = 1
alpha = 0
if lm < 0.1*lmopt:
lm = 0.1*lmopt
lt = lmt - lm*np.cos(alpha)
fse = ms.force_se(lt=lt, ltslack=ltslack)
fpe = ms.force_pe(lm=lm/lmopt)
fl = ms.force_l(lm=lm/lmopt)
fce_t = fse/np.cos(alpha) - fpe
vm = ms.velo_fm(fm=fce_t, a=a, fl=fl)
return vm
def fm_eq(lm, lmd, lmt):
fm0 = ms.P['fm0']
lmopt = ms.P['lmopt']
ltslack = ms.P['ltslack']
a = 1
alpha = 0
lt = lmt - lm*np.cos(alpha)
fl = ms.force_l(lm=lm/lmopt)
fpe = ms.force_pe(lm=lm/lmopt)
fm = ms.force_vm(vm=lmd, fl=fl, lmopt=lmopt, a=a) + fpe
fm = fm*fm0
return fm
Let's instantiate the muscles class:
ms = muscles.Thelen2003()
ms.set_parameters()
ms.set_states()
ms.muscle_plot();
The parameters were successfully loaded and are stored in the variable P. The states were successfully loaded and are stored in the variable S.
Let's input the initial states and use scipy.odeint to solve the ODEs:
lmthetaomega = [0.087, np.pi/2, 0]
time = np.arange(0, .12, 0.001)
data = odeint(onelink_eq, lmthetaomega, time)
Plots of the simulated angular position and velocity:
def sim_plot(time, data, ms):
datam = []
for i, t in enumerate(time):
fm0 = ms.P['fm0']
lmopt = ms.P['lmopt']
ltslack = ms.P['ltslack']
a = 1
alpha = 0
lmt0 = 0.310
lm = data[i, 0]
theta = data[i, 1]
lmt = lmt0 - rm_fun(theta)*(theta - np.pi/2)
lt = lmt - lm*np.cos(alpha)
fl = ms.force_l(lm=lm/lmopt)
fpe = ms.force_pe(lm=lm/lmopt)
fse = ms.force_se(lt=lt, ltslack=ltslack)
fce_t = fse/np.cos(alpha) - fpe
vm = ms.velo_fm(fm=fce_t, a=a, fl=fl, lmopt=lmopt)
fm = ms.force_vm(vm=vm, fl=fl, lmopt=lmopt, a=a) + fpe
d = [t, lmt, lm, lt, vm, fm*fm0, fse*fm0, a*fl*fm0, fpe*fm0, alpha]
datam.append(d)
datam = np.array(datam)
fig, axs = plt.subplots(nrows=1, ncols=2, sharex = True, figsize=(9, 4))
axs[0].plot(time, data[:, 1]*180/np.pi)
axs[0].set_xlabel('Time (s)')
axs[0].set_ylabel('Knee angle $(^o)$')
axs[1].plot(time, data[:, 2]*180/np.pi)
axs[1].set_xlabel('Time (s)')
axs[1].set_ylabel('Knee velocity $(^o/s)$')
plt.tight_layout()
plt.show()
return axs, datam
axs, data2 = sim_plot(time, data, ms)
And the plots for the simulated muscle mechanics:
axs_lm = ms.lm_plot(data2)
vas_int_r = np.loadtxt('./../data/vas_int_r.mot', skiprows=7)
print('Shape of vas_int_r:', vas_int_r.shape)
Shape of vas_int_r: (100, 3)
We need to be able to calculate the moment arm for any angle, not only for the 100 values in these data. Let's fit a spline to these data, which will return a function we can use to calculate the moment arm at any angle:
from scipy import interpolate
S = interpolate.InterpolatedUnivariateSpline(vas_int_r[:, 1], vas_int_r[:, 2])
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(7, 4))
ax.plot(vas_int_r[:, 1], vas_int_r[:, 2], label='Raw data')
ax.plot(vas_int_r[:, 1], S(vas_int_r[:, 1]), 'r--', label='Spline')
ax.set_xlabel('Knee angle $(^o)$')
ax.set_ylabel('Moment arm (m)')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
It works as expected, we just have to handle the fact that the angle range is different.
Let's define a new function for the moment arm for our simulation:
# define a function for the moment arm
def rm_fun(theta, data=S):
"""Vastus intermedius moment arm."""
rm = S(theta*np.pi/180 - np.pi)
return rm
data = odeint(onelink_eq, lmthetaomega, time)
axs, data2 = sim_plot(time, data, ms)
axs_lm2 = ms.lm_plot(data2) # axs_lm
References¶
- Nigg BM and Herzog W (2006) Biomechanics of the Musculo-skeletal System. 3rd Edition. Wiley.
- Zajac FE, Gordon ME (1989) Determining muscle's force and action in multi-articular movement. Exercise and Sport Sciences Reviews, 17, 187-230.