%pylab inline
Populating the interactive namespace from numpy and matplotlib
from sympy import *
from pylab import *
import matplotlib.pyplot as plt
from sympy.interactive import printing
printing.init_printing(use_latex=True)
from IPython.display import display
a,x,Z = symbols('a,x,Z')
Problem 1¶
1D¶
The partition function for 1D system is
$Z = \sum_i e^{-\beta E_i}$
The probability on a state $E_i$
In our case, there are only two possible energy states, $E_1 = -\mu B$, $E_2 = \mu B$. So the magnetization is
Write magnetization as a function of $T$ and $T$.
$M$ vs $T$ Plots¶
To plot $M~T$, we need to make a quantity with dimension of $T$ . $\bar T = \mu B/k_B$ will do the work.
in which, $\bar M = \mu N$ .
At $T \rightarrow \infty $ limit, we have the magnetization $M$ is 0. This is because high temperature distroys the alignment of dipoles.
tanh(0)
At $T\rightarrow \infty$, we have $\frac{M}{\bar M}$ 1.
tanh(inf)
At very low temperature, the dipoles have no random motion so all dipoles aligned together thus $M$ is 1.
Now plot out this result.
t = linspace(0, 100, 1000)
mt = tanh(1/t)
fig11 = plt.figure()
axes = fig11.add_axes([0.1, 0.1, 0.8, 0.8]) # left, bottom, width, height (range 0 to 1)
axes.plot(t, mt, 'r')
axes.set_xlabel('T bar')
axes.set_ylabel('M bar')
axes.set_title('M ~ T');
-c:2: RuntimeWarning: divide by zero encountered in divide
This plot agrees with our results of the limits.
$M$ vs $B$ Plots¶
Define a unit magnetic induction $\bar B = k_B T/\mu$. Write the magnetization as a function of $B$.
At the limit of $B\rightarrow 0$, we have $M\rightarrow 0$, which is because no magnetic field is there to align the dipoles. (No interactions between dipoles.)
At the limit of $B\rightarrow \infty$, we have $M\rightarrow 1$, which is because infinite magnetic field can align all the dipoles to one direction no matter how strong the thermal random motion is.
Plot the result.
b = linspace(0, 5, 100)
mb = tanh(b)
fig12 = plt.figure()
axes = fig12.add_axes([0.1, 0.1, 0.8, 0.8]) # left, bottom, width, height (range 0 to 1)
axes.plot(b, mb, 'r')
axes.set_xlabel('B/Bbar')
axes.set_ylabel('M/Mbar')
axes.set_title('M ~ B');
Heat Capacity¶
Energy of the system is
t13e = linspace(0, 5, 100)
e1 = -tanh(t13e)
fig13e = plt.figure()
axes = fig13e.add_axes([0.1, 0.1, 0.8, 0.8]) # left, bottom, width, height (range 0 to 1)
axes.plot(t13e, e1, 'r')
axes.set_xlabel('T/Tbar')
axes.set_ylabel('E/Ebar')
axes.set_title('E ~ T');
Heat capacity is
t13 = linspace(0, 5, 100)
c1 = tanh(t13)
fig13 = plt.figure()
axes = fig13.add_axes([0.1, 0.1, 0.8, 0.8]) # left, bottom, width, height (range 0 to 1)
axes.plot(t13, c1, 'r')
axes.set_xlabel('T/Tbar')
axes.set_ylabel('C/Cbar')
axes.set_title('C ~ T');
2D¶
The energy of a dipole can be written as $E(\theta) = -\mu B \cos\theta$, in which $\theta$ is the angle between the dipole and magnetic field.
Partition function is
where $\mathrm{BesselI}$ is the modified Bessel function of the first kind.
Then we can calculate magnetization, which is given by
The result given by Mathematica is (so bad that I can't make sympy to deal with such integrations.)
Energy should be
Heat capacity is the derivitive of energy over temperature.
Plot out these results using Mathematica.
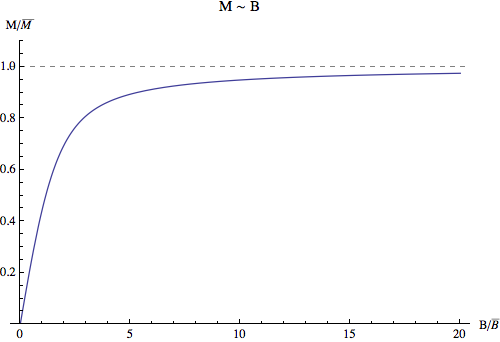
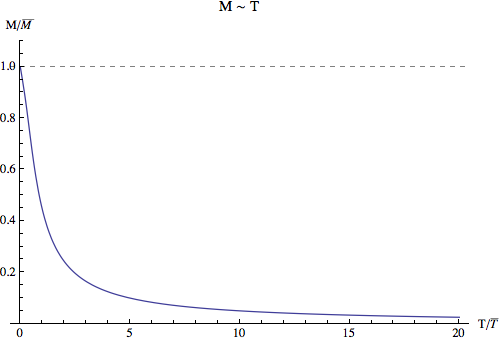
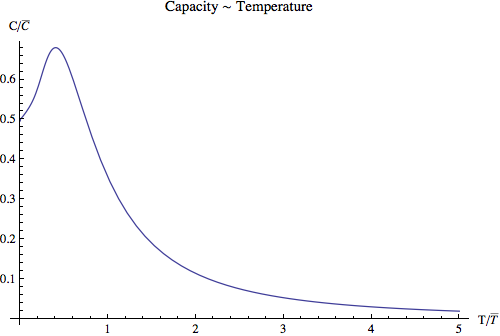
3D¶
Energy of a dipole is $E(\theta) = -\mu B \cos\theta$.
Then we can calculate the partition function, which is
Magnetization is
where $\bar B = \frac{1}{\mu \beta}$. Define $\bar M = \mu N$ .Then we can write down the dimensionless equation, which is
Total energy is
Take the derivative with respect to temperature, we have the heat capacity.
Plot out the results.
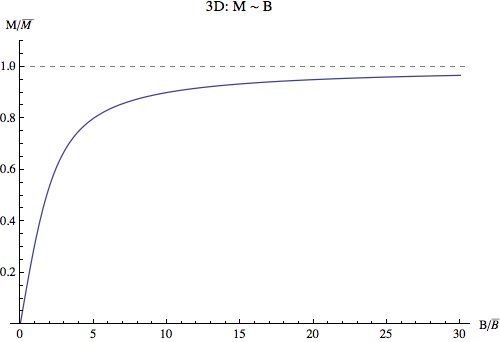
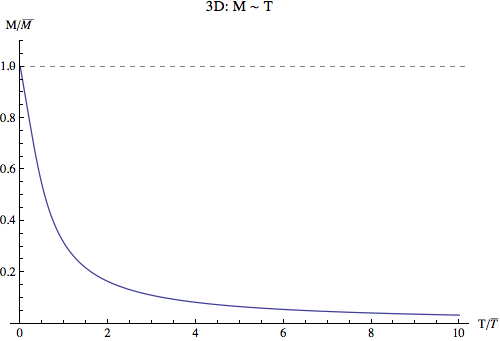
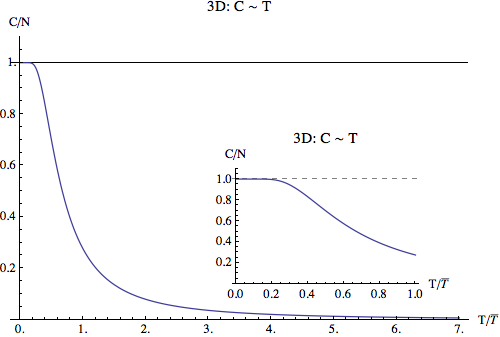
Problem 2¶
First law of thermodynamics¶
Energy can be transfered from one form to another, or from one system to another, but can never be disapear. The total energy of a closed system is conserved. For any infinitesimal process, the change of internal energy is equivalent to the sum of work done to other systems and heat obsorbed from other systems, which is to say, in the language of mathematiccs,
$$ \mathrm d U = \mathrm d Q + \mathrm d W $$¶
Entropy¶
Basicly, at high temperature and in large systems, entropy is the dominant of all marco properties of a system. Entropy indicates the reversibility of a process, defines Kelvin and restricts us from reaching absolute zero.
The most important property of entropy is that it is a function that only depends on state of the system not the path. This property can lead us to many interesting results.
Free energy¶
As I have learned in undergrad stat mech, free energy is a quantity defined to make our life easier when dealing with systems which has fixed temperature and fixed volume. In that case, free energy can never grow larger. Mathematically,
Suppose we have a gas system going through a reversible process, free energy
For fixed $T$ and $V$, we have $\mathrm d F = 0$. For irreversible process, it is less than 0.
Chemical potential¶
Chemical potential is the increased Gibbs free energy when one mole particle is added to the system.