Space Invasion, Space Invaders, and Climate Change Mitigation¶
Scott Jeen¶
Jesus College MCR, 3rd June 2021¶
Abstract
Recent advances in the field of Reinforcement Learning, a subfield of Artificial Intelligence, have shown computers can achieve superhuman performance at complex games like Go, Starcraft and the Atari Suite without human knowledge. What if, instead of playing Space Invaders, we play the game of climate change mitigation? More specifically, how can we design games where the goal is to minimise carbon emissions in some setting, and learn to play them optimally? In this talk, we'll first establish the importance of using less energy and material to limit planet-cooking, then we'll take the first steps toward formulating a game whose solution could help to mitigate climate change.
0. Prerequisites¶
- Agree that runaway climate change is worth avoiding
- Willing to accept approximations/back-of-the-envelope calcs
- Able to look beyond my UK-centric lens
0. Outline¶
1. Space Invasion: the footprint of climate change mitigation
2. Space Invaders: learning to control complex systems optimally
3. An Emission-minimisation Game
Every good university course begins with some prerequisites, and despite this talk being conducted in a dining room, today will be no different. I expect three things from you all this evening: 1) That you agree runaway climate change is something worth avoiding, I only say this because I will not be discussing why it's worth avoiding, and I'll assume we're all on the same page, thinking together about the best strategies for doing so. Number 2) I expect that you will willingly accept my sometimes poor back-of-the-envelope calculations; the first half of this talk will be about sustainable energy at a national, or international scale, and to make the presentation of that information more relatable the numbers are often rounded to one significant figure. And finally prerequisite number 3), this talk focusses mainly on the United Kingdom, despite the fact the problem is global, and despite the fact the UK's role in climate change mitigation is almost unimportant when compared with other larger countries. I hope that despite this, findings related to the UK can generalise to all countries, as we all have to face these challenges at some stage or other.
If we're all happy with the prerequisites, let's begin with the first topic from the talk title: space invasion.
1. Space Invasion¶
Climate change mitigation is fundamentally an energy problem; society requires energy of all forms to function, and this energy still comes largely from sources that emit greenhouse gases that cause global warming. With that in mind, we can think of energy as the calories of our economies, and we can frame climate change mitigation as a diet that we must embark on. Like any diet, there are three things we can do to lose weight. Firstly, we can eat healthier meals, or get our energy from cleaner sources. We can think of this as analogous to generating energy from renewable energy resources like wind or solar. Secondly, we can eat less food, or use less energy in our lives. In our research group we call this Resource Efficiency, or maintaning the same final service for less energy input. And finally, we can keep eat the same rubbish food in similar amounts, and just exercise a few hours a day to try and burn off the calories. This is analgoous to carbon capture and storage, where we continue to emit carbon dioxide by burning fossil fuels, but attach a hoover to the exhaust of the power station or industrial process and bury the gases in the same oilfield you just plucked the fossil fuels from. Guess which option big oil like the best.
So these are our options. The UK has focussed largely on option 1 (renewable energy) to-date, and all of their projections rely on option 3 (carbon capture), little attention is given to motivating resource efficiency; in much the same way people prefer not to tell you to eat less when dieting. I'm going to talk initially about the problems associated with the UK's plans, and how my research looks to address it.
High Carb(on) Diet¶
High Carb(on) Diet¶

To do that, I need to introduce you to our unit of measurement for this diet. Instead of using the colorie, we'll use the kilowatt-hour (kWh), the SI unit for measuring energy. To give you a sense of scale, here's our current energy diet, and the number of kWhs associated with some everyday activities.
Leaving one 40W lightbulb on for 24 hours will use about 1kWh of energy. An aluminium can of coke requires about 0.6kWh of energy to be produced. A hot bath will cost you 5kWh. And burning 1 litre of petrol in your car by driving 5 or 6 miles will use 10kWh of energy. If we sum all activities you do daily, we find that the average person in the UK uses about 125kWh/day. Instead of quantifying energy use on a daily basis, we can convert this volume of energy to a flow rate of energy that we call power, measured in watts rather than watt-hours. So 125kWh/day of energy is equivalent to a 5kW power source being consuming power for the whole day, similar to two cookers being left at 200 degrees all day.
So this is your life, two cookers on all the time, one for the left hemisphere of your brain and one for the right. So to continue to live your life as you do today, you need to go out in the world and find a 5kW power source and have it on all day, offsetting the energy you are using elsewhere in your life. So let's think about doing that; if you're going to go out and find a source of power, your going to need a piece of land to put in on. How much land would you like? Well let's give everyone in the country a fair share of land.
Our Energy Diet¶
💡 → 1kWh
🥤 → 0.6kWh
🛁 → 5kWh
🚗 → 10kWh
💁♀️ → 125kWh/day or 5kW → 🎛🎛
after MacKay (2008)
The population of the UK is 66.65 million apparently, and the total area of land in the UK is 242,495 square kilometres. If we divide the top one by the bottom one, we find that each person in the UK gets about 3600 square metres of space to store their energy generating devices, which is about equivalent to half a football pitch. We can do one more calculation to find the power density of your life: by taking the power rating of your life (5kW) and dividing it by your allotment size (3600m2) we find that your life costs 2.5 W/m2.
Now, this is a useful figure to obtain, because each of those energy generating devices you're about to go and source are also quantified in this way, so we see how likely it is for each of the technologies to power your life.
Your Allotment for Growing Energy¶
- UK population: 66.65 million
- UK land area: 242,495 km²
- Your allotment: 3600m² ~ half a football pitch
- Your life: ~2.5 W/m$^2$

after MacKay (2008)
Here's a table of the most common energy generating technologies. The middle column is their power density, or power output per unit land area, and the final column is an indication of whether they are zero-emission or otherwise. (The pinnochio face is reserved for technologies that are often said to be renewable, but are, in fact, not). So, remember you're life requires 2.5 W/m2, what the first entry in the table is telling us is that to power your life using solely wind power we need to cover your entire allotment (and everyone else's allotment) is wind turbines. If we wanted to use solar power, we'd need to cover about half of your football pitch in solar panels. If we wanted to use nuclear power, we would only need to use about 1% of your football pitch. And so on. So let's try and visualise some of these interventions.
Energy Space Requirements¶
Your life: ~2.5 W/m$^2$
| Technology | ~ Power Per Unit Land Area | Zero Operational Emissions |
|---|---|---|
| Wind | 2.7 W/m$^2$ | 💚 |
| Biomass | 1 W/m$^2$ | 🤥 |
| Solar | 6 W/m$^2$ | 💚 |
| Hydropower | 0.9 W/m$^2$ | 🤥 |
| Geothermal | 3 W/m$^2$ | 💚 |
| Natural Gas | 1300 W/m$^2$ | ⛔️ |
| Coal | 125 W/m$^2$ | ⛔️ |
| Oil | 180 W/m$^2$ | ⛔️ |
| Nuclear | 300 W/m$^2$ | 💚 |
Data: van Zalk & Behrens (2018)
Here's your football pitch:

If you want to reserve some space for living your life, rather than just producing energy, you'll want to corden that off. Here's is 40% of your land blocked off, which represents the area of UK land currently used for cities and for countryside Bossard & Otahel (2000).
But we'll find later on that we might need some of that land to avoid turning the UK into a desert, so it's back on the table for now:

Let's take a look at how this land has been used through the years. This was (very) roughly the UK between the beginning of the industrial revolution and the 1980s. Most electricity coming from coal, and oil used for transportation and some heating.
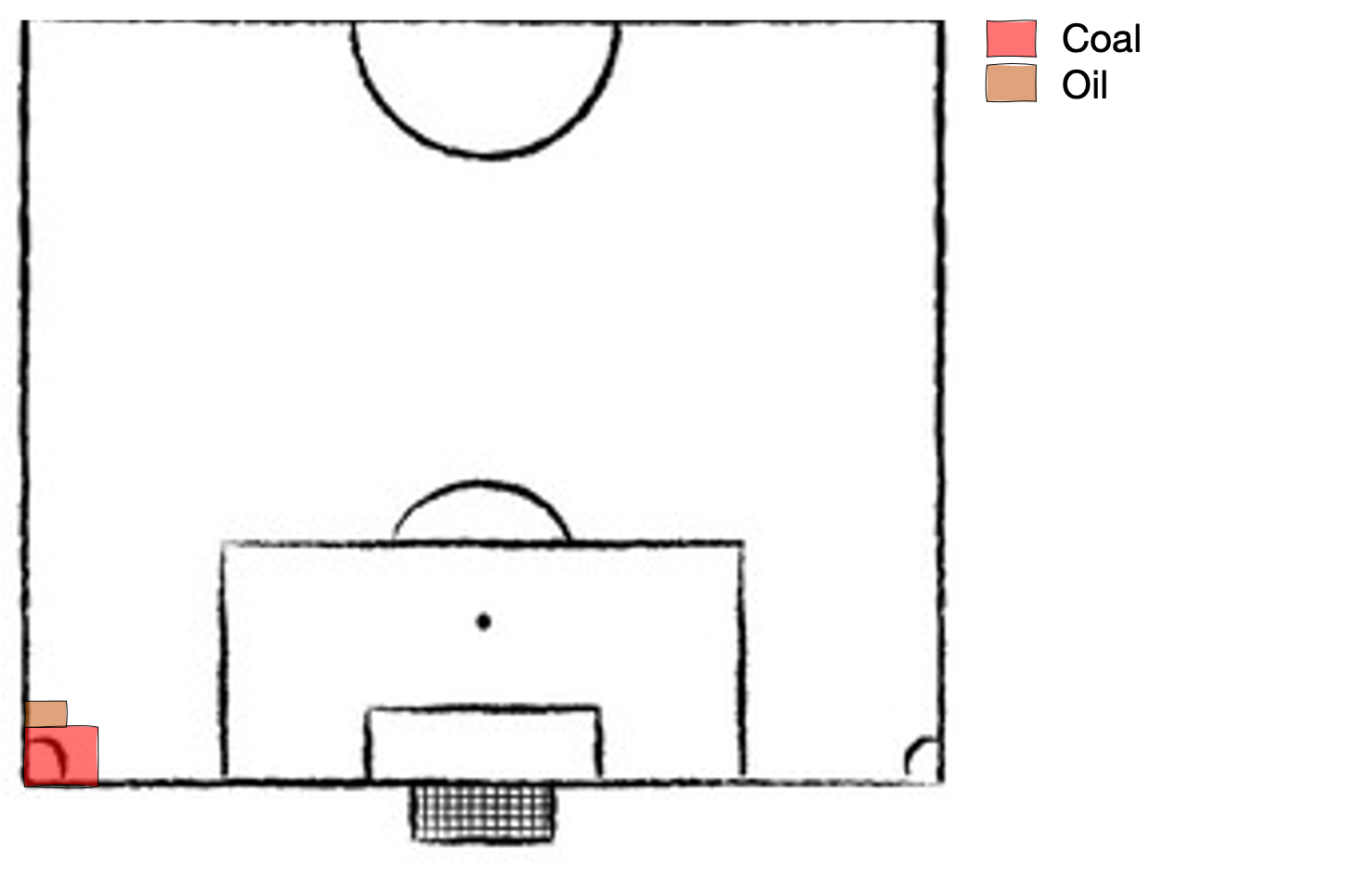
Then Mrs Thatcher came to power in the 1980s, closed most of the coal mines and replaced them with natural gas power plants of higher power densithy and lower emission intensity, and the energy mix looked something like this. Note: energy generation is using approximately 1% of land area here, plenty of room to continue live out the glorious 80s whilst the planet slowly begins to simmer.
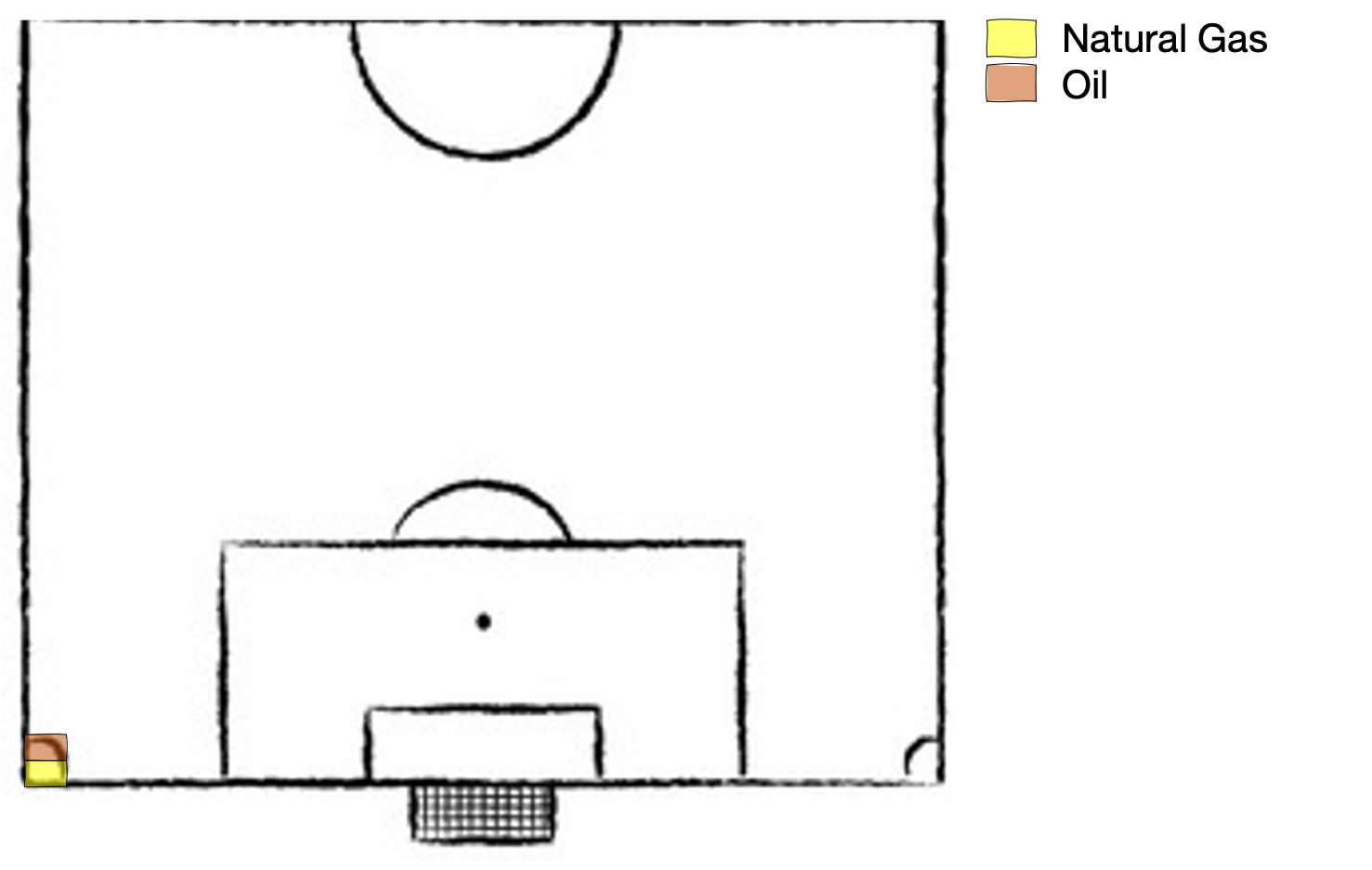
Here's (very) roughly where we are today, we have a mix of natural gas, biomass, wind, solar and nuclear; with the area of land they cover flattered by the fact that 40% of our energy is sourced from natural gas. The important takeaway from this diagram is the arbitrarily sized chequered box representing imported energy. Much of the goods and services that contribute to your 125kWh per day energy usage are imported; the aluminimum in your coke can, the steel in your car. To fund our lifestyles in the UK, we are effectively outsourcing a large amount of energy production (and associated emissions), moving the energy generating devices from our land to somebody else's land. This may be okay today, when the energy generating devices elsewhere are natural gas or coal and don't take up much land. But when these countries attempt to decarbonise and find they are being asked or required to build solar panels on their countryside, I suspect they are going to come back to the UK and say 'wait a minute, you deal with these emissions, you're causing them'. This gives us a false sense of how much land the energy required to fuel our lifestyles is taking up.
So, to me, it seems only fair that we consider scenarios where we generate an amount of energy proportional to our lifestyles. And that is what we will consider now.

If we were to generate energy using only wind and solar, we would use approximately 70% of UK land area, remember cities and countryside account for 40% of land area so we are eating into our leisure area now.

There are various ways to stop this space invasion, and one of them is to shrink the size of the energy pie; to use less energy in our society; to be more resource efficient. That is the focus of our research group's work, and that is one of the goals of my research. So, if we want to reduce our energy demand, what are our options, and where should our prioritises lie.
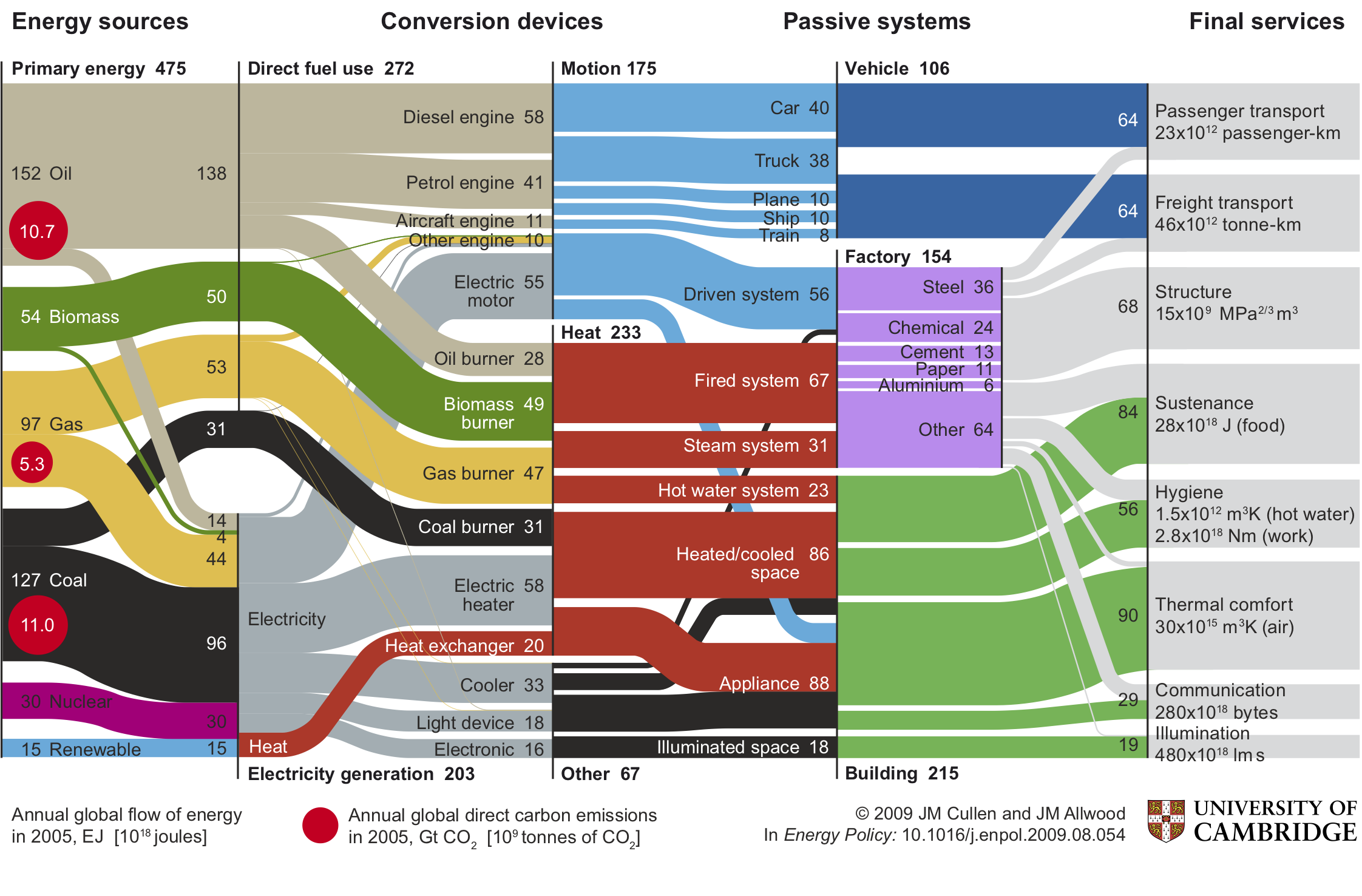
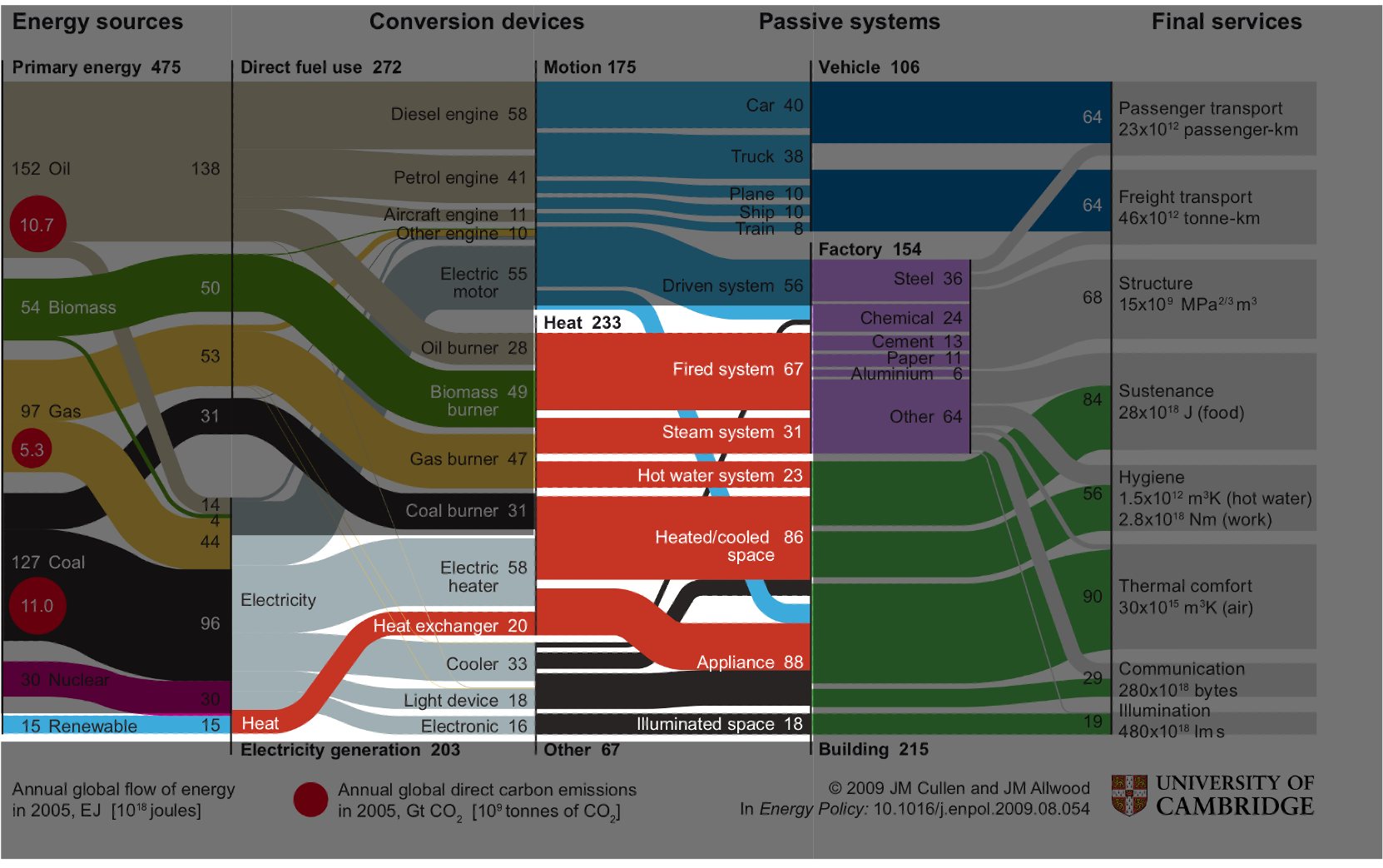
So if we need to reduce our energy demand, what are our options? Well, earlier I discussed the average energy demand of someone in the UK and the summation of a bunch of different tasks, jobs or activities we conduct throughout the day. We can think of these tasks as services, and it is the use of these services we can alter to reduce our energy demand.
Above, is work done by my supervisor, Jon Cullen, in 2010, mapping the relationship between energy sources and final services, via the devices that produce this transformation. I'd like to first focus your attention on the middle slice of the five illustrated. You'll see that approximately half of global energy supply is used to produce or extract heat (red); the most obvious example of this being in the heating and cooling of homes, other examples include powering furnaces in manufacuturing facilities, or in heating water. Just over a third of our energy is used to produce motion (cyan), be it powering cars, trucks or planes, or in moving heavy machinery in manufacuturing. And just over 15% of energy remains for what Jon describes as 'Other' (black) which involves lighting, communication, and myriad of less energy-intensive services.
So the big-ticket items for energy reduction are in changing how we move, and changing how we regulate temperature. In general, there's two change we can make: 1) Increase the efficiency of energy-converting devices such that they demand less energy for the same final service, or 2) Decrease energy-use altogether, either in the production or use phases of a final service.
An example of the former, in the context or personal car use would be increasing the thermodynamic efficiency of the engine such that the car uses less fuel to cover the same distance. An example of the later would be driving the car for fewer miles, or using less steel in construction of the vehicle.
My research looks to affect two parts of this diagram, I'll discuss both in turn.
The first is the small cyan line in the bottom left hand corner: renewable energy, and its integration with energy conversion devices, and final services. Although small on this diagram, this was the global energy mix in 2005, by 2050 we expect renewable energy to supply approximately 70% of world energy. Unlike fossil fuel power stations, we cannot control when renewable energy resources will produce electricity because their ability to produce energy is weather dependent. For example, solar panels will produce energy during the daytime when the sun has risen, but not at night when the sun has set. We therefore say renewable energy technologies are intermittent. I'll explain the intermittency problem visually:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import interpolate
%matplotlib inline
import scipy.stats as stats
from scipy.interpolate import interp1d
from matplotlib import animation, rc
from IPython.display import HTML
# time series
x = np.linspace(0,24,25)
x_new = np.linspace(0,24,250)
# demand
demand = [1,1,1,1,1,1,2,6,3,2,2,2,1,1,1,1,1,4,7,9,8,6,3,1,0]
f = interp1d(x, demand, kind='cubic')
demand_new = f(x_new)
# grid
grid_mu = 12
grid_sig = 4
grid = stats.norm.pdf(x_new, grid_mu, grid_sig) * 100
# figure
with plt.xkcd():
fig = plt.figure(figsize=(15,6))
ax = plt.subplot(1,1,1)
ax.set_xlabel('time (hrs)')
ax.set_ylabel('power')
plt.yticks([])
plt.xticks([0,6,12,18,24])
ax.set_xlim((0,24))
ax.set_ylim((0,12))
line1, = ax.plot([], [], label='demand')
line2, = ax.plot([], [], label='supply')
plt.legend()
# animation function
def drawframe(n=int):
x1 = x_new[:n]
y1 = demand_new[:n]
y2 = grid[:n]
line1.set_data(x1, y1)
line2.set_data(x1, y2)
return (line1, line2)
# create animation
rc('animation', html='html5')
anim = animation.FuncAnimation(fig, drawframe, frames=len(x_new), interval=50)
# anim.save('images/intermittency.gif')
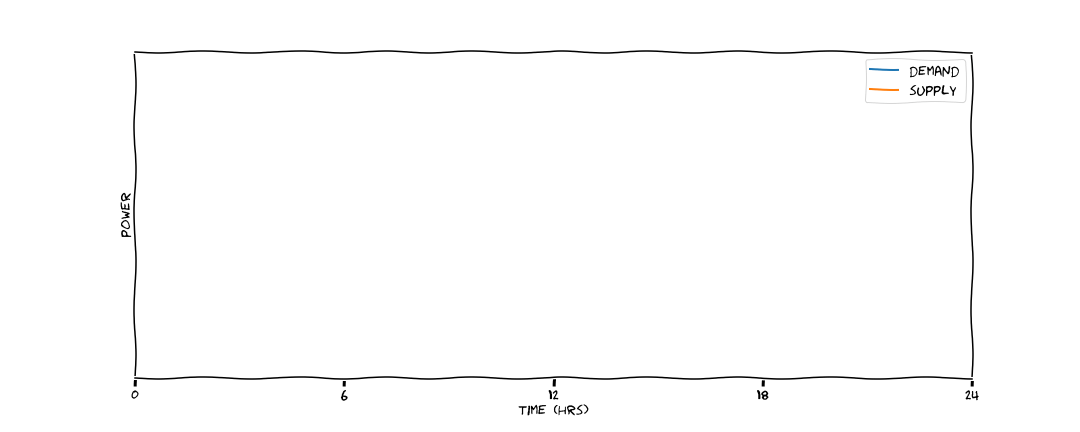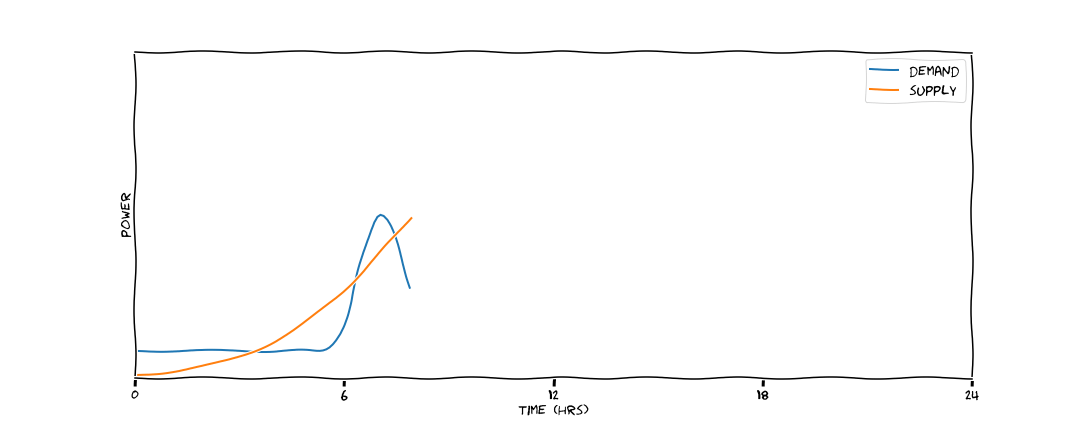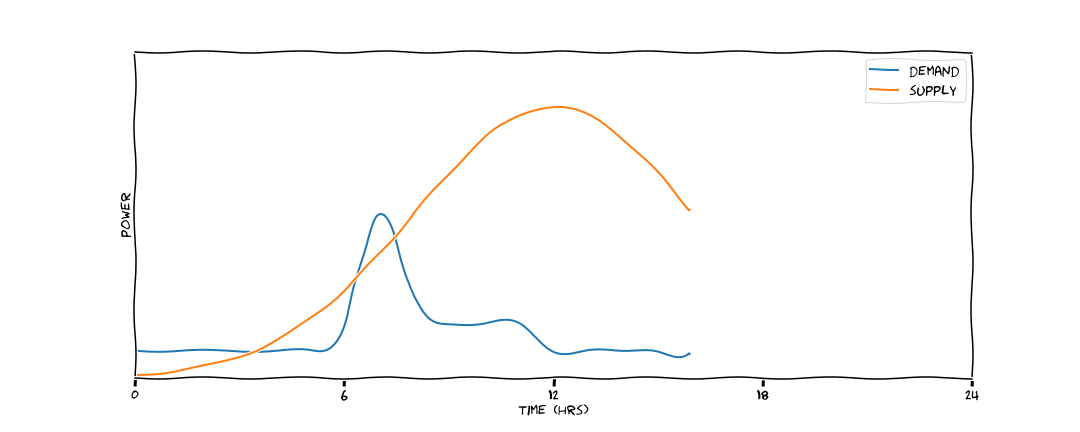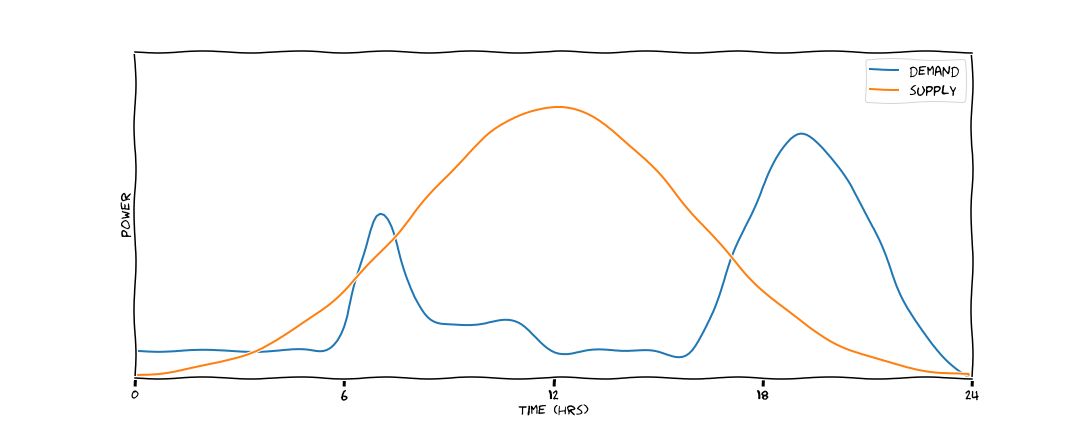
Let's consider the problem of trying to power a flat on Park Street for one day using a 10kW array of solar panels on the roof. The orange line here traces power output of the panels throughout the day, when the sun rises in the morning it begins to produce energy, it's power output peaks at some point in the early afternoon and then drops to 0 after the sun has set. In contrast the energy demand of the flat occupants is lumpy, there's a peak around 7am when people get in the shower and put the kettle on for a coffee; if they go out to work for the day the power demand drops in the morning and afternoon, then when they come home and putting the heating, oven and tv in there's another spike.
The Intermittency Problem¶
# create fill between plot
with plt.xkcd():
fig = plt.figure(figsize=(15,6))
ax = plt.subplot(1,1,1)
ax.set_xlabel('time (hrs)')
ax.set_ylabel('power')
plt.yticks([])
plt.xticks([0,6,12,18,24])
ax.set_xlim((0,24))
ax.set_ylim((0,12))
ax.plot(x_new, demand_new, label='demand')
ax.plot(x_new, grid, label='supply')
plt.fill_between(x_new, grid, demand_new, where=(demand_new>grid), color='red', alpha=0.2, label='deficit')
plt.fill_between(x_new, grid, demand_new, where=(demand_new<grid), color='green', alpha=0.2, label='surplus')
plt.legend()
plt.savefig('images/intermittency.png', dpi=300)
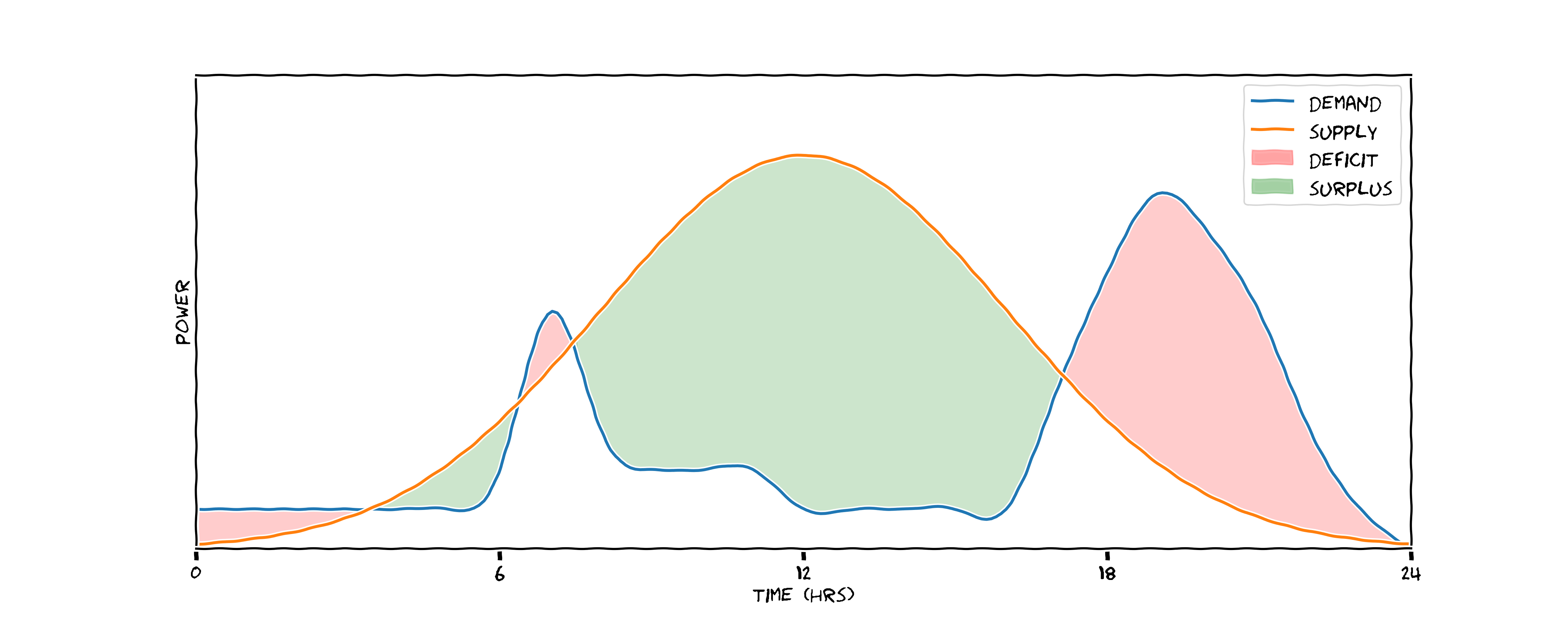
This creates scenarios throughout the day where there are deficits and surplusses in energy. In green, energy generation exceeds demand, so we meet our energy requirements renewably, but in the absence of a battery waste chunks of zero-emission energy. In red, demand outstrips what the panels supply. In these scenarios today, these peaks of excess supply are met by firing up natural gas plants at short notice to provide the energy, creating further emissions.
demand_new_2 = stats.norm.pdf(x_new, grid_mu, 6) * 80
# create fill between plot
with plt.xkcd():
fig = plt.figure(figsize=(15,6))
ax = plt.subplot(1,1,1)
ax.set_xlabel('time (hrs)')
ax.set_ylabel('power')
plt.yticks([])
plt.xticks([0,6,12,18,24])
ax.set_xlim((0,24))
ax.set_ylim((0,12))
ax.plot(x_new, demand_new_2, label='demand')
ax.plot(x_new, grid, label='supply')
plt.fill_between(x_new, grid, demand_new_2, where=(demand_new_2>grid), color='blue', alpha=0.1, label='discharged')
plt.fill_between(x_new, grid, demand_new_2, where=(demand_new_2<grid), color='orange', alpha=0.2, label='stored')
plt.legend()
plt.savefig('images/opt_intermittency.png', dpi=300)
What we would prefer is a scenaario like this one. Here we've done two things: we flattened and broadened the demand curve, so there are no peaks to meet with natural gas; and we've introduced a storage medium - potentially a battery. During the hours of peak production we store energy (represented by orange) and we discharge this energy when needed, represented in blue. Here we've reduced our total energy demand by flattening the peak, and we've stopped the mitigated the problem of peak matching with natural gas - saving emissions in two ways.

This is of course an idealised representation of what we'd like to do at both a household and national scale, and it makes it look simpler that it is. In reality, both the the supply curve and the demand curve are stochastic, and matching them is a highly complex optimisation problem.
To do so we need to accurately predict renewable energy supply at various time horizons; in the next 5 minutes and in the next 5 hours, and everywhere in between. Equally we need to predict energy demand, which, depending on the situation can be affected by countless variables. In the household setting, the energy demand is largely affected by weather conditions (i.e. if it's cold outside heating demand increases) and time of day (if it's 7am somebody probably wants a shower). In the industrial setting, perhaps a car manufacturing plant, the energy demand of the plant may be affected by sales forecasts, and raw material delivery schedules.
Attempting to solve this problem requires some sophisticated techniques, and my research centres on a subfield of artificial intelligence called Reinforcement Learning (RL). Which I'll take about now, in section 2: space invaders.
Intermittency: A non-trivial optimsation problem¶
Stochastic supply:
- Weather-dependent
- Need accurate predictions of supply at varied time horizons: 5mins; 5 hours; 5 days
Stochastic demand:
- Depending on scenario, affected by countless variables
- Household setting: outdoor temperature; time of day; day of week
- Industrial setting: sales forecasts; raw material delivery schedules
2. Space Invaders¶
Reinforcement learning is the eminent paradigm for allowing computers to learn from experience. In RL, we consider an agent (represented by the brain) interacting with an environment (represented by the globe). The agent can take actions in an environment, and at each timestep step it receives feedback on how the state of the environment has changed given that action, and a reward for taking that action. The goal of the RL agent is to maximise the sum of cumulative rewards throughout its lifetime. When an RL agent is instantiated, it has no understanding of its environment or valuable actions to take in the environment, but learns by taking actions in the environment, in a trial and error fashion, observing the reward it accrues, and updating it's understanding of the state-space. It's hypothesised that this is much the same way we as humans learn intelligently. Consider the example of learning to ride a bike; we don't necessarily understand the physics of bike-riding, instead we get on the bike, try and balance and cycle and see what works for us. We find, through trial and error, the optimal way to position our body to balance the bike.
Although this appears a simple paradigm, it elicits extremelely powerful behaviour from computers.
Some of the best examples of this powerful behaviour come from the gaming domain. Here's an RL agent, created by DeepMind in 2013, that learns to play the Atari game breakout with no prior knowledge or human input. The agent is fed minimal data; it's fed the raw pixels of the screen as a representation of the state; it's knows it can take three actions: move left, move right, or stay still, and it's fed the score at the top of the screen as a reward signal.
You can see initially it struggles to hit the ball, but slowly it learns first to connect with the ball. Then by episode 600 it exhibits some pretty intelligent behaviour; it discovers that the optimally strategy is to burrow holes in the channels of the bricks and ping the ball behind the bricks.
from IPython.display import YouTubeVideo
YouTubeVideo('TmPfTpjtdgg', height=400, width=800)
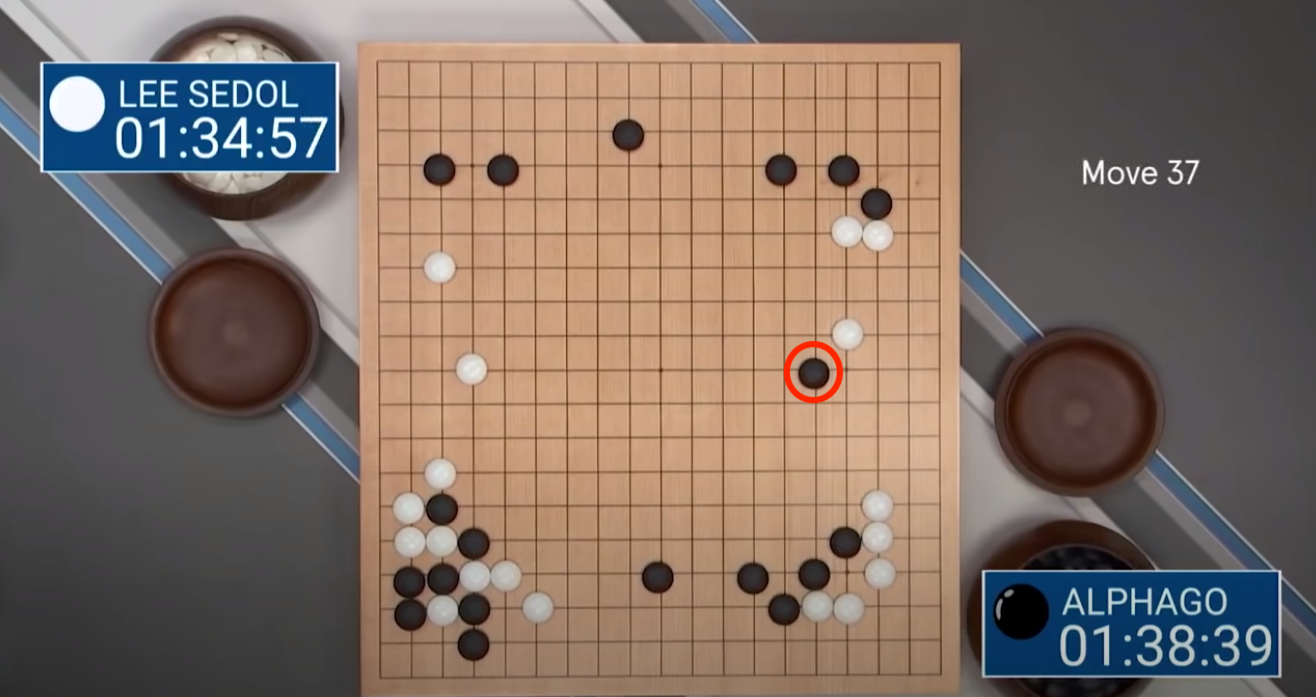
Here's another example, a few years later DeepMind created a Go-playing agent and played the world no.1 Lee Sedol in a 5 match series in South Korea. Go is considerably more complex game than chess; instead of an 8x8 board you have a 19x19 board, meaning the number of state permutations is astronimical. You can arrange the Go board in roughly $10^(170)$ permutations which is more atoms that are in the observable universe, meaning if you were to store each state permutation in a computer you would need one larger than the size of our universe.
AlphaGo beat Lee Sedol 4-1 having trained on a few millions episodes of game play, but perhaps the most intersting aspect of their match was the now infamous move 37 played by AlphaGo. On top is the board arrangement at move 37, apparently the most humans believe that with this board set-up the optimal stragey is the play in the margins, and avoid moving too close to the centre. AlphaGo elected to play 5 columns in from the margin, which flummoxed Lee Sedol and the audience of spectators, so much so that he had to go outside for a cigarette.
As the game evolved this move proved to be crucial. The board evolved in such that this black piece won AlphaGo the game, it from the near-infinite trajectories this game could have gone down, AlphaGo had correctly predicted the most likely. Not only did AlphaGo win the game, but it taught humans something about a complex system that we hadn't appreciated in the 3000 years we've been playing the game of Go, and to me that's really exciting.
To give you a little more intuition about what is happening under the hood of an RL agent, let's return quickly to the breakout example.
There are various ways in which the agent can represent its understanding of the system, but one is by assinging each part of the state-space (the environment) a value, and iterating it's formulation of that value as it receives rewards from the environment.
Here we see a plot of the agent's value estimate for the current state of the environment over time. We see a spikey pattern in the value estimate; just before the ball hits it bricks it has learned that it will receive reward shortly and estimates high value, then the value estimate drops as it knows it would receive more reward until some time into the future.
YouTubeVideo('DG17IKcDt8c', height=400, width=800)
3. An Emission-Minimising Game¶
So I've introduced RL, and discussed how agents can learn to play extremely complex games with no prior knowledge to a superhuman level. I've also motivated the need to reduce energy-use as a climate change mitigation technique. I'm going to conclude by combining these two sections together, and discuss formulating an emission-minimising game and how we can go about formulating a solution.
3.1 Formulating the Game¶
- Moves:
- Chiller control
- $\sum_{n=1}^6 a_t^n \in \mathcal{A}$, with $\mathcal{A} = [0\text{kW}, 5\text{kW}]$
- Goal:
- Minimise energy-use
- $\min{E_t}$, whilst
- Maintain temperature
- $T_t \leq 3^0C$
- Environment Dynamics:
- ?
Learning the Game Dynamics¶

3.2 Playing the Game¶
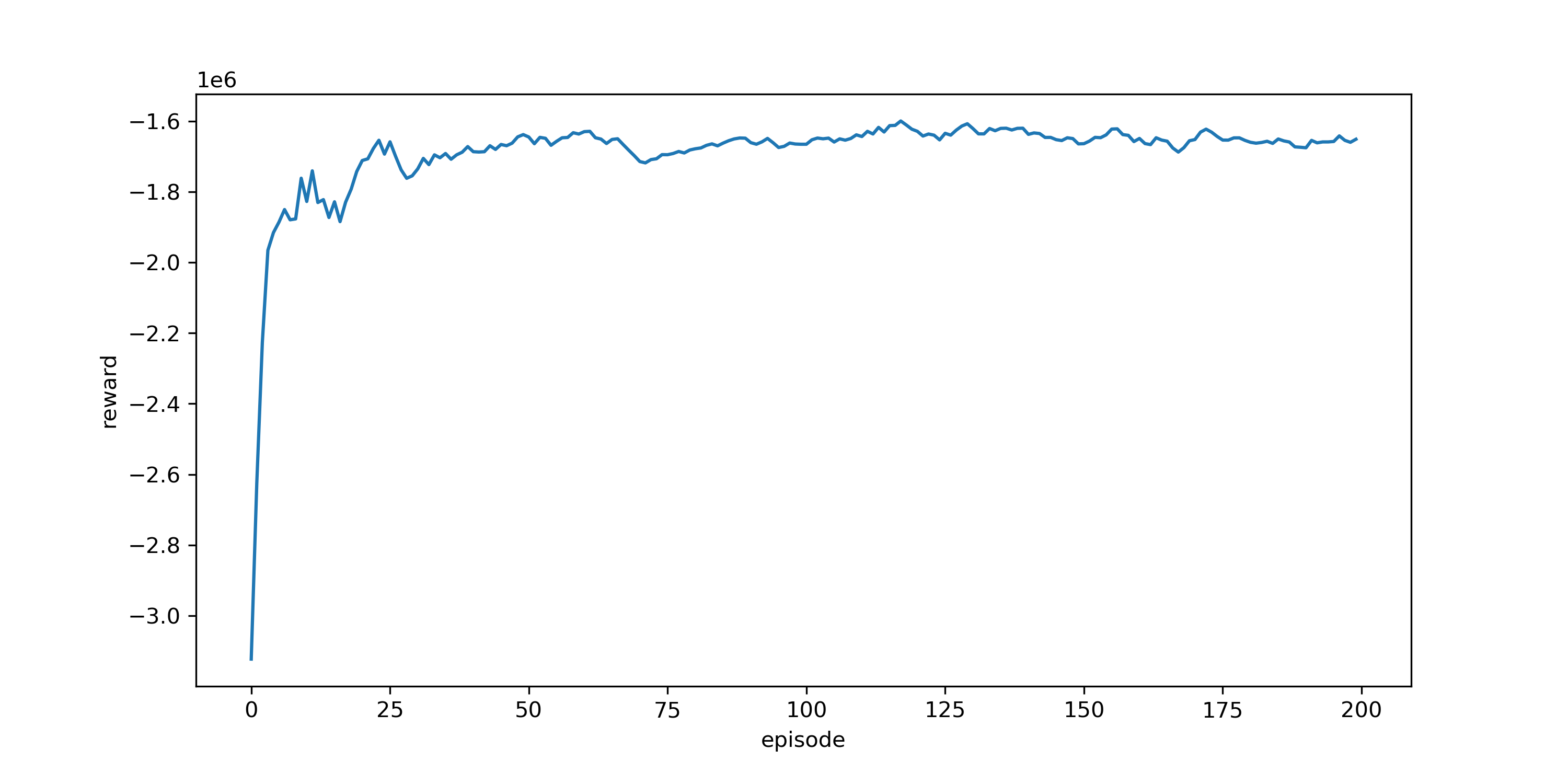
3.3. Winning the Game¶


3.4 Next Steps¶
- Incorportating grid randomness
- Incorporating uncertainty
- Online, data-efficient learning
- Multi-agent systems
Thanks!¶
References¶
Bossard, M., Feranec, J., & Otahel, J. (2000). CORINE land cover technical guide: Addendum 2000.
Cullen, J. M., & Allwood, J. M. (2010). The efficient use of energy: Tracing the global flow of energy from fuel to service. Energy Policy, 38(1), 75-81.
MacKay, D. (2008). Sustainable Energy-without the hot air. UIT cambridge.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602.
Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., ... & Hassabis, D. (2017). Mastering the game of go without human knowledge. nature, 550(7676), 354-359.
Silver, D. (2015). Lecture 1: Introduction to reinforcement learning. Google DeepMind, 1, 1-10.
van Zalk, J., & Behrens, P. (2018). The spatial extent of renewable and non-renewable power generation: A review and meta-analysis of power densities and their application in the US. Energy Policy, 123, 83-91.