3. Topic Modeling with NMF and SVD¶

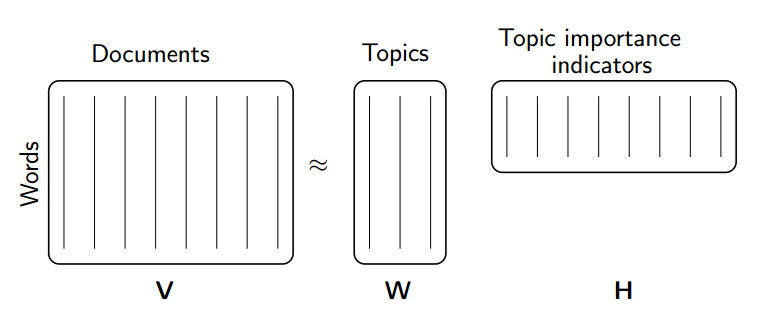
Topic modeling is a great way to get started with matrix factorizations. We start with a term-document matrix:

(source: [Introduction to Information Retrieval](http://player.slideplayer.com/15/4528582/#))

We can decompose this into one tall thin matrix times one wide short matrix (possibly with a diagonal matrix in between).

Notice that this representation does not take into account word order or sentence structure. It's an example of a bag of words approach.

Motivation¶

Consider the most extreme case - reconstructing the matrix using an outer product of two vectors. Clearly, in most cases we won't be able to reconstruct the matrix exactly. But if we had one vector with the relative frequency of each vocabulary word out of the total word count, and one with the average number of words per document, then that outer product would be as close as we can get.

Now consider increasing that matrices to two columns and two rows. The optimal decomposition would now be to cluster the documents into two groups, each of which has as different a distribution of words as possible to each other, but as similar as possible amongst the documents in the cluster. We will call those two groups "topics". And we would cluster the words into two groups, based on those which most frequently appear in each of the topics.

In today's class¶

We'll take a dataset of documents in several different categories, and find topics (consisting of groups of words) for them. Knowing the actual categories helps us evaluate if the topics we find make sense.

We will try this with two different matrix factorizations: Singular Value Decomposition (SVD) and Non-negative Matrix Factorization (NMF)

In [1]:

import numpy as np
from sklearn.datasets import fetch_20newsgroups
from sklearn import decomposition
from scipy import linalg
import matplotlib.pyplot as plt

In [2]:

%matplotlib inline
np.set_printoptions(suppress=True)

Additional Resources¶

Data source: Newsgroups are discussion groups on Usenet, which was popular in the 80s and 90s before the web really took off. This dataset includes 18,000 newsgroups posts with 20 topics.
Chris Manning's book chapter on matrix factorization and LSI
Scikit learn truncated SVD LSI details

Set up data¶

Scikit Learn comes with a number of built-in datasets, as well as loading utilities to load several standard external datasets. This is a great resource, and the datasets include Boston housing prices, face images, patches of forest, diabetes, breast cancer, and more. We will be using the newsgroups dataset.

Newsgroups are discussion groups on Usenet, which was popular in the 80s and 90s before the web really took off. This dataset includes 18,000 newsgroups posts with 20 topics.

In [3]:

categories = ['alt.atheism', 'talk.religion.misc', 'comp.graphics', 'sci.space']
remove = ('headers', 'footers', 'quotes')
newsgroups_train = fetch_20newsgroups(subset='train', categories=categories, remove=remove)
newsgroups_test = fetch_20newsgroups(subset='test', categories=categories, remove=remove)

In [4]:

newsgroups_train.filenames.shape, newsgroups_train.target.shape

Out[4]:

((2034,), (2034,))

Let's look at some of the data. Can you guess which category these messages are in?

In [55]:

print("\n".join(newsgroups_train.data[:3]))

Hi,

I've noticed that if you only save a model (with all your mapping planes
positioned carefully) to a .3DS file that when you reload it after restarting
3DS, they are given a default position and orientation.  But if you save
to a .PRJ file their positions/orientation are preserved.  Does anyone
know why this information is not stored in the .3DS file?  Nothing is
explicitly said in the manual about saving texture rules in the .PRJ file. 
I'd like to be able to read the texture rule information, does anyone have 
the format for the .PRJ file?

Is the .CEL file format available from somewhere?

Rych


Seems to be, barring evidence to the contrary, that Koresh was simply
another deranged fanatic who thought it neccessary to take a whole bunch of
folks with him, children and all, to satisfy his delusional mania. Jim
Jones, circa 1993.


Nope - fruitcakes like Koresh have been demonstrating such evil corruption
for centuries.

 >In article <1993Apr19.020359.26996@sq.sq.com>, msb@sq.sq.com (Mark Brader) 

MB>                                                             So the
MB> 1970 figure seems unlikely to actually be anything but a perijove.

JG>Sorry, _perijoves_...I'm not used to talking this language.

Couldn't we just say periapsis or apoapsis?

hint: definition of perijove is the point in the orbit of a satellite of Jupiter nearest the planet's center

In [249]:

np.array(newsgroups_train.target_names)[newsgroups_train.target[:3]]

Out[249]:

array(['comp.graphics', 'talk.religion.misc', 'sci.space'], 
      dtype='<U18')

The target attribute is the integer index of the category.

In [5]:

newsgroups_train.target[:10]

Out[5]:

array([1, 3, 2, 0, 2, 0, 2, 1, 2, 1])

In [6]:

num_topics, num_top_words = 6, 8

Next, scikit learn has a method that will extract all the word counts for us.

In [7]:

from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer

In [8]:

vectorizer = CountVectorizer(stop_words='english')
vectors = vectorizer.fit_transform(newsgroups_train.data).todense() # (documents, vocab)
vectors.shape #, vectors.nnz / vectors.shape[0], row_means.shape

Out[8]:

(2034, 26576)

In [343]:

print(len(newsgroups_train.data), vectors.shape)

2034 (2034, 26576)

In [9]:

vocab = np.array(vectorizer.get_feature_names())

In [10]:

vocab.shape

Out[10]:

(26576,)

In [11]:

vocab[7000:7020]

Out[11]:

array(['cosmonauts', 'cosmos', 'cosponsored', 'cost', 'costa', 'costar',
       'costing', 'costly', 'costruction', 'costs', 'cosy', 'cote',
       'couched', 'couldn', 'council', 'councils', 'counsel', 'counselees',
       'counselor', 'count'],
      dtype='<U80')

Singular Value Decomposition (SVD)¶

"SVD is not nearly as famous as it should be." - Gilbert Strang

We would clearly expect that the words that appear most frequently in one topic would appear less frequently in the other - otherwise that word wouldn't make a good choice to separate out the two topics. Therefore, we expect the topics to be orthogonal.

The SVD algorithm factorizes a matrix into one matrix with orthogonal columns and one with orthogonal rows (along with a diagonal matrix, which contains the relative importance of each factor).

(source: [Facebook Research: Fast Randomized SVD](https://research.fb.com/fast-randomized-svd/))

SVD is an exact decomposition, since the matrices it creates are big enough to fully cover the original matrix. SVD is extremely widely used in linear algebra, and specifically in data science, including:

semantic analysis
collaborative filtering/recommendations (winning entry for Netflix Prize)
calculate Moore-Penrose pseudoinverse
data compression
principal component analysis (will be covered later in course)

In [12]:

%time U, s, Vh = linalg.svd(vectors, full_matrices=False)

CPU times: user 1min 4s, sys: 8.82 s, total: 1min 13s
Wall time: 13.3 s

In [13]:

print(U.shape, s.shape, Vh.shape)

(2034, 2034) (2034,) (2034, 26576)

Confirm this is a decomposition of the input.

Answer¶

In [346]:

#Exercise: confrim that U, s, Vh is a decomposition of the var Vectors

Out[346]:

True

Confirm that U, V are orthonormal

Answer¶

In [246]:

#Exercise: Confirm that U, Vh are orthonormal

Out[246]:

True

Topics¶

What can we say about the singular values s?

In [96]:

plt.plot(s);

In [97]:

plt.plot(s[:10])

Out[97]:

[<matplotlib.lines.Line2D at 0x7fcada6c6828>]

In [52]:

num_top_words=8

def show_topics(a):
    top_words = lambda t: [vocab[i] for i in np.argsort(t)[:-num_top_words-1:-1]]
    topic_words = ([top_words(t) for t in a])
    return [' '.join(t) for t in topic_words]

In [347]:

show_topics(Vh[:10])

Out[347]:

['critus ditto propagandist surname galacticentric kindergarten surreal imaginative',
 'jpeg gif file color quality image jfif format',
 'graphics edu pub mail 128 3d ray ftp',
 'jesus god matthew people atheists atheism does graphics',
 'image data processing analysis software available tools display',
 'god atheists atheism religious believe religion argument true',
 'space nasa lunar mars probe moon missions probes',
 'image probe surface lunar mars probes moon orbit',
 'argument fallacy conclusion example true ad argumentum premises',
 'space larson image theory universe physical nasa material']

We get topics that match the kinds of clusters we would expect! This is despite the fact that this is an unsupervised algorithm - which is to say, we never actually told the algorithm how our documents are grouped.

We will return to SVD in much more detail later. For now, the important takeaway is that we have a tool that allows us to exactly factor a matrix into orthogonal columns and orthogonal rows.

Non-negative Matrix Factorization (NMF)¶

Motivation¶

(source: NMF Tutorial)

A more interpretable approach:

(source: NMF Tutorial)

Idea¶

Rather than constraining our factors to be orthogonal, another idea would to constrain them to be non-negative. NMF is a factorization of a non-negative data set $V$: $$ V = W H$$ into non-negative matrices $W,\; H$. Often positive factors will be more easily interpretable (and this is the reason behind NMF's popularity).

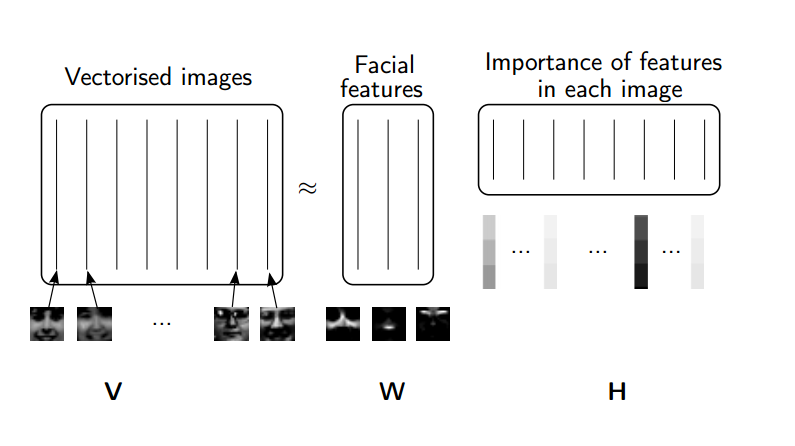
(source: NMF Tutorial)

Nonnegative matrix factorization (NMF) is a non-exact factorization that factors into one skinny positive matrix and one short positive matrix. NMF is NP-hard and non-unique. There are a number of variations on it, created by adding different constraints.

Applications of NMF¶

Face Decompositions
Collaborative Filtering, eg movie recommendations
Audio source separation
Chemistry
Bioinformatics and Gene Expression
Topic Modeling (our problem!)

(source: NMF Tutorial)

More Reading:

The Why and How of Nonnegative Matrix Factorization

NMF from sklearn¶

First, we will use scikit-learn's implementation of NMF:

In [13]:

m,n=vectors.shape
d=5  # num topics

In [363]:

clf = decomposition.NMF(n_components=d, random_state=1)

W1 = clf.fit_transform(vectors)
H1 = clf.components_

In [296]:

show_topics(H1)

Out[296]:

['jpeg image gif file color images format quality',
 'edu graphics pub mail 128 ray ftp send',
 'space launch satellite nasa commercial satellites year market',
 'jesus matthew prophecy people said messiah david isaiah',
 'image data available software processing ftp edu analysis',
 'god atheists atheism religious believe people religion does']

TF-IDF¶

Topic Frequency-Inverse Document Frequency (TF-IDF) is a way to normalize term counts by taking into account how often they appear in a document, how long the document is, and how commmon/rare the term is.

TF = (# occurrences of term t in document) / (# of words in documents)

IDF = log(# of documents / # documents with term t in it)

In [ ]:

vectorizer_tfidf = TfidfVectorizer(stop_words='english')
vectors_tfidf = vectorizer_tfidf.fit_transform(newsgroups_train.data) # (documents, vocab)

In [263]:

W1 = clf.fit_transform(vectors_tfidf)
H1 = clf.components_

In [255]:

show_topics(H1)

Out[255]:

['don people just think like know say religion',
 'thanks graphics files image file program windows format',
 'space nasa launch shuttle orbit lunar moon earth',
 'ico bobbe tek beauchaine bronx manhattan sank queens',
 'god jesus bible believe atheism christian does belief',
 'objective morality values moral subjective science absolute claim']

In [26]:

plt.plot(clf.components_[0])

Out[26]:

[<matplotlib.lines.Line2D at 0x7f0e1039a7b8>]

In [27]:

clf.reconstruction_err_

Out[27]:

43.71292605795277

NMF in summary¶

Benefits: Fast and easy to use!

Downsides: took years of research and expertise to create

Notes:

For NMF, matrix needs to be at least as tall as it is wide, or we get an error with fit_transform
Can use df_min in CountVectorizer to only look at words that were in at least k of the split texts

NMF from scratch in numpy, using SGD¶

Gradient Descent¶

The key idea of standard gradient descent:

Randomly choose some weights to start
Loop:
- Use weights to calculate a prediction
- Calculate the derivative of the loss
- Update the weights
Repeat step 2 lots of times. Eventually we end up with some decent weights.

Key: We want to decrease our loss and the derivative tells us the direction of steepest descent.

Note that loss, error, and cost are all terms used to describe the same thing.

Let's take a look at the Gradient Descent Intro notebook (originally from the fast.ai deep learning course).

Stochastic Gradient Descent (SGD)¶

Stochastic gradient descent is an incredibly useful optimization method (it is also the heart of deep learning, where it is used for backpropagation).

For standard gradient descent, we evaluate the loss using all of our data which can be really slow. In stochastic gradient descent, we evaluate our loss function on just a sample of our data (sometimes called a mini-batch). We would get different loss values on different samples of the data, so this is why it is stochastic. It turns out that this is still an effective way to optimize, and it's much more efficient!

We can see how this works in this excel spreadsheet (originally from the fast.ai deep learning course).

Resources:

SGD Lecture from Andrew Ng's Coursera ML course
fast.ai wiki page on SGD
Gradient Descent For Machine Learning (Jason Brownlee- Machine Learning Mastery)
An overview of gradient descent optimization algorithms

Applying SGD to NMF¶

Goal: Decompose $V\;(m \times n)$ into $$V \approx WH$$ where $W\;(m \times d)$ and $H\;(d \times n)$, $W,\;H\;>=\;0$, and we've minimized the Frobenius norm of $V-WH$.

Approach: We will pick random positive $W$ & $H$, and then use SGD to optimize.

To use SGD, we need to know the gradient of the loss function.

Sources:

Optimality and gradients of NMF: http://users.wfu.edu/plemmons/papers/chu_ple.pdf
Projected gradients: https://www.csie.ntu.edu.tw/~cjlin/papers/pgradnmf.pdf

In [272]:

lam=1e3
lr=1e-2
m, n = vectors_tfidf.shape

In [252]:

W1 = clf.fit_transform(vectors)
H1 = clf.components_

In [253]:

show_topics(H1)

Out[253]:

['jpeg image gif file color images format quality',
 'edu graphics pub mail 128 ray ftp send',
 'space launch satellite nasa commercial satellites year market',
 'jesus matthew prophecy people said messiah david isaiah',
 'image data available software processing ftp edu analysis',
 'god atheists atheism religious believe people religion does']

In [265]:

mu = 1e-6
def grads(M, W, H):
    R = W@H-M
    return R@H.T + penalty(W, mu)*lam, W.T@R + penalty(H, mu)*lam # dW, dH

In [266]:

def penalty(M, mu):
    return np.where(M>=mu,0, np.min(M - mu, 0))

In [267]:

def upd(M, W, H, lr):
    dW,dH = grads(M,W,H)
    W -= lr*dW; H -= lr*dH

In [268]:

def report(M,W,H): 
    print(np.linalg.norm(M-W@H), W.min(), H.min(), (W<0).sum(), (H<0).sum())

In [348]:

W = np.abs(np.random.normal(scale=0.01, size=(m,d)))
H = np.abs(np.random.normal(scale=0.01, size=(d,n)))

In [349]:

report(vectors_tfidf, W, H)

44.4395133509 5.67503308167e-07 2.49717354504e-07 0 0

In [350]:

upd(vectors_tfidf,W,H,lr)

In [351]:

report(vectors_tfidf, W, H)

44.4194155587 -0.00186845669883 -0.000182969569359 509 788

In [352]:

for i in range(50): 
    upd(vectors_tfidf,W,H,lr)
    if i % 10 == 0: report(vectors_tfidf,W,H)

44.4071645597 -0.00145791197281 -0.00012862260312 343 1174
44.352156176 -0.000549676823494 -9.16363641124e-05 218 4689
44.3020593384 -0.000284017335617 -0.000130903875061 165 9685
44.2468609535 -0.000279317810433 -0.000182173029912 169 16735
44.199218 -0.000290092649623 -0.000198140867356 222 25109

In [281]:

show_topics(H)

Out[281]:

['cview file image edu files use directory temp',
 'moral like time does don software new years',
 'god jesus bible believe objective exist atheism belief',
 'thanks graphics program know help looking windows advance',
 'space nasa launch shuttle orbit station moon lunar',
 'people don said think ico tek bobbe bronx']

This is painfully slow to train! Lots of parameter fiddling and still slow to train (or explodes).

PyTorch¶

PyTorch is a Python framework for tensors and dynamic neural networks with GPU acceleration. Many of the core contributors work on Facebook's AI team. In many ways, it is similar to Numpy, only with the increased parallelization of using a GPU.

From the PyTorch documentation:

Further learning: If you are curious to learn what dynamic neural networks are, you may want to watch this talk by Soumith Chintala, Facebook AI researcher and core PyTorch contributor.

If you want to learn more PyTorch, you can try this tutorial or this learning by examples.

Note about GPUs: If you are not using a GPU, you will need to remove the .cuda() from the methods below. GPU usage is not required for this course, but I thought it would be of interest to some of you. To learn how to create an AWS instance with a GPU, you can watch the fast.ai setup lesson.

In [282]:

import torch
import torch.cuda as tc
from torch.autograd import Variable

In [283]:

def V(M): return Variable(M, requires_grad=True)

In [284]:

v=vectors_tfidf.todense()

In [285]:

t_vectors = torch.Tensor(v.astype(np.float32)).cuda()

In [286]:

mu = 1e-5

In [287]:

def grads_t(M, W, H):
    R = W.mm(H)-M
    return (R.mm(H.t()) + penalty_t(W, mu)*lam, 
        W.t().mm(R) + penalty_t(H, mu)*lam) # dW, dH

def penalty_t(M, mu):
    return (M<mu).type(tc.FloatTensor)*torch.clamp(M - mu, max=0.)

def upd_t(M, W, H, lr):
    dW,dH = grads_t(M,W,H)
    W.sub_(lr*dW); H.sub_(lr*dH)

def report_t(M,W,H): 
    print((M-W.mm(H)).norm(2), W.min(), H.min(), (W<0).sum(), (H<0).sum())

In [354]:

t_W = tc.FloatTensor(m,d)
t_H = tc.FloatTensor(d,n)
t_W.normal_(std=0.01).abs_(); 
t_H.normal_(std=0.01).abs_();

In [355]:

d=6; lam=100; lr=0.05

In [356]:

for i in range(1000): 
    upd_t(t_vectors,t_W,t_H,lr)
    if i % 100 == 0: 
        report_t(t_vectors,t_W,t_H)
        lr *= 0.9

44.392791748046875 -0.0060190423391759396 -0.0004986411076970398 1505 2282
43.746803283691406 -0.009054708294570446 -0.011047963984310627 2085 23854
43.702056884765625 -0.008214150555431843 -0.014783496037125587 2295 24432
43.654273986816406 -0.006195350084453821 -0.006913348101079464 2625 22663
43.646759033203125 -0.004638500511646271 -0.003197424579411745 2684 23270
43.645320892333984 -0.005679543130099773 -0.00419645756483078 3242 24199
43.6449089050293 -0.0041352929547429085 -0.00843129213899374 3282 25030
43.64469528198242 -0.003943094052374363 -0.00745873199775815 3129 26220
43.64459991455078 -0.004347225651144981 -0.007400824688374996 3031 26323
43.64434051513672 -0.0039044099394232035 -0.0067480215802788734 3930 33718

In [291]:

show_topics(t_H.cpu().numpy())

Out[291]:

['objective morality values moral subjective science absolute claim',
 'god jesus bible believe atheism christian does belief',
 'ico bobbe tek bronx beauchaine manhattan sank queens',
 'thanks graphics files image file program windows know',
 'space nasa launch shuttle orbit lunar moon earth',
 'don people just think like know say religion']

In [292]:

plt.plot(t_H.cpu().numpy()[0])

Out[292]:

[<matplotlib.lines.Line2D at 0x7fe4173f1d68>]

In [1328]:

t_W.mm(t_H).max()

Out[1328]:

0.43389660120010376

In [1329]:

t_vectors.max()

Out[1329]:

0.9188119769096375

PyTorch: autograd¶

Above, we used our knowledge of what the gradient of the loss function was to do SGD from scratch in PyTorch. However, PyTorch has an automatic differentiation package, autograd which we could use instead. This is really useful, in that we can use autograd on problems where we don't know what the derivative is.

The approach we use below is very general, and would work for almost any optimization problem.

In PyTorch, Variables have the same API as tensors, but Variables remember the operations used on to create them. This lets us take derivatives.

PyTorch Autograd Introduction¶

Example taken from this tutorial in the official documentation.

In [375]:

x = Variable(torch.ones(2, 2), requires_grad=True)
print(x)

Variable containing:
 1  1
 1  1
[torch.FloatTensor of size 2x2]

In [376]:

print(x.data)

 1  1
 1  1
[torch.FloatTensor of size 2x2]

In [377]:

print(x.grad)

Variable containing:
 0  0
 0  0
[torch.FloatTensor of size 2x2]

In [378]:

y = x + 2
print(y)

Variable containing:
 3  3
 3  3
[torch.FloatTensor of size 2x2]

In [383]:

z = y * y * 3
out = z.sum()
print(z, out)

Variable containing:
 27  27
 27  27
[torch.FloatTensor of size 2x2]
 Variable containing:
 108
[torch.FloatTensor of size 1]

In [382]:

out.backward()
print(x.grad)

Variable containing:
 18  18
 18  18
[torch.FloatTensor of size 2x2]

In [ ]:

Using Autograd for NMF¶

In [167]:

lam=1e6

In [168]:

pW = Variable(tc.FloatTensor(m,d), requires_grad=True)
pH = Variable(tc.FloatTensor(d,n), requires_grad=True)
pW.data.normal_(std=0.01).abs_()
pH.data.normal_(std=0.01).abs_();

In [357]:

def report():
    W,H = pW.data, pH.data
    print((M-pW.mm(pH)).norm(2).data[0], W.min(), H.min(), (W<0).sum(), (H<0).sum())

def penalty(A):
    return torch.pow((A<0).type(tc.FloatTensor)*torch.clamp(A, max=0.), 2)

def penalize(): return penalty(pW).mean() + penalty(pH).mean()

def loss(): return (M-pW.mm(pH)).norm(2) + penalize()*lam

In [358]:

M = Variable(t_vectors).cuda()

In [359]:

opt = torch.optim.Adam([pW,pH], lr=1e-3, betas=(0.9,0.9))
lr = 0.05
report()

43.66044616699219 -0.0002547535696066916 -0.00046720390673726797 319 8633

How to apply SGD, using autograd:

In [361]:

for i in range(1000): 
    opt.zero_grad()
    l = loss()
    l.backward()
    opt.step()
    if i % 100 == 99: 
        report()
        lr *= 0.9     # learning rate annealling

43.628597259521484 -0.022899555042386055 -0.26526615023612976 692 82579
43.62860107421875 -0.021287493407726288 -0.2440912425518036 617 77552
43.628597259521484 -0.020111067220568657 -0.22828206419944763 576 77726
43.628604888916016 -0.01912039890885353 -0.21654289960861206 553 84411
43.62861251831055 -0.018248897045850754 -0.20736189186573029 544 75546
43.62862014770508 -0.01753264293074608 -0.19999365508556366 491 78949
43.62862777709961 -0.016773322597146034 -0.194113627076149 513 83822
43.628639221191406 -0.01622121036052704 -0.18905577063560486 485 74101
43.62863540649414 -0.01574397087097168 -0.18498440086841583 478 85987
43.628639221191406 -0.015293922275304794 -0.18137598037719727 487 74023

In [362]:

h = pH.data.cpu().numpy()
show_topics(h)

Out[362]:

['god jesus bible believe atheism christian belief does',
 'thanks graphics files image file windows program format',
 'just don think people like ve graphics religion',
 'objective morality values moral subjective science absolute claim',
 'ico bobbe tek beauchaine bronx manhattan sank queens',
 'space nasa shuttle launch orbit lunar moon data']

In [174]:

plt.plot(h[0]);

Comparing Approaches¶

Scikit-Learn's NMF¶

Fast
No parameter tuning
Relies on decades of academic research, took experts a long time to implement

source: [Python Nimfa Documentation](http://nimfa.biolab.si/)

Using PyTorch and SGD¶

Took us an hour to implement, didn't have to be NMF experts
Parameters were fiddly
Not as fast (tried in numpy and was so slow we had to switch to PyTorch)

Truncated SVD¶

We saved a lot of time when we calculated NMF by only calculating the subset of columns we were interested in. Is there a way to get this benefit with SVD? Yes there is! It's called truncated SVD. We are just interested in the vectors corresponding to the largest singular values.

(source: [Facebook Research: Fast Randomized SVD](https://research.fb.com/fast-randomized-svd/))

Shortcomings of classical algorithms for decomposition:¶

Matrices are "stupendously big"
Data are often missing or inaccurate. Why spend extra computational resources when imprecision of input limits precision of the output?
Data transfer now plays a major role in time of algorithms. Techniques the require fewer passes over the data may be substantially faster, even if they require more flops (flops = floating point operations).
Important to take advantage of GPUs.

(source: Halko)

Advantages of randomized algorithms:¶

inherently stable
performance guarantees do not depend on subtle spectral properties
needed matrix-vector products can be done in parallel

(source: Halko)

3. Topic Modeling with NMF and SVD¶

Motivation¶

In today's class¶

Additional Resources¶

Other Tutorials¶

Set up data¶

Singular Value Decomposition (SVD)¶

Answer¶

Answer¶

Topics¶

Non-negative Matrix Factorization (NMF)¶

Motivation¶

Idea¶

Applications of NMF¶

NMF from sklearn¶

TF-IDF¶

NMF in summary¶

NMF from scratch in numpy, using SGD¶

Gradient Descent¶

Stochastic Gradient Descent (SGD)¶

Applying SGD to NMF¶

PyTorch¶

PyTorch: autograd¶

PyTorch Autograd Introduction¶

Using Autograd for NMF¶

Comparing Approaches¶

Scikit-Learn's NMF¶

Using PyTorch and SGD¶

Truncated SVD¶

Shortcomings of classical algorithms for decomposition:¶

Advantages of randomized algorithms:¶

End¶