MANUAL DE LABORATORIO DE COMUNICACIONES DIGITALES: PYTHON¶
F. Javier Payán Somet, Juan José Murillo-Fuentes, José Carlos Aradillas Jaramillo
Departamento de Teoría de la Señal y Comunicaciones
Escuela Técnica Superior de Ingeniería
Universidad de Sevilla
Tema 3. Test de Hipótesis¶
Este notebook contiene código del Tema 3
Inicialización¶
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Numpy ≥1.16 is required
import numpy as np
assert np.__version__ >= "1.16"
Probabilidad de error¶
Probabilidad de error en el caso binario¶
Código 3.2
# Rango de valores del vector de observación
paso = 1e-6
r = np.arange(-10,10,paso)
# Probabilidades a priori
P_0=1/4
P_1=1-P_0
# Valores de la variable aleatoria mensaje
X_0 = -2
X_1 = +2
# Varianza del ruido aditivo en el canal
vza = 1;
# Funciones densidad de probabilidad condicionales
f_0 = (1/(np.sqrt(2*np.pi*vza)))*np.exp(-((r-X_0)**2)/(2*vza)) # Caso X=X_0
f_1 = (1/(np.sqrt(2*np.pi*vza)))*np.exp(-((r-X_1)**2)/(2*vza)) # Caso X=X_1
"""Alternativamente
from labcomdig import fdpnormal
f_0 = fdpnormal(r,X_0,vza)
f_1 = fdpnormal(r,X_1,vza)
"""
# Encontrar la frontera de la región de decisión g con el detector MAP
indexUmbral = np.where(P_1*f_1 > P_0*f_0)[0][0]
g = r[indexUmbral]
""" Alternativamente
g = r[np.where(P_1*f_1 > P_0*f_0)][0]
#Primer valor (índice [0]) en el que P1f1>P0f0
"""
print('Cálculo de la probabilidad de error con ruido gaussiano y caso binario')
print('Umbral MAP, g: {:.2f}'.format(g))
# Calcular las integrales de manera aproximada
PC_0 = np.sum(f_0[:indexUmbral])*paso # Pb de detección correcta si se transmite un cero
PC_1 = np.sum(f_1[indexUmbral:])*paso # Pb de detección correcta si se transmite un uno
"""Alternativamente
from scipy.integrate import quad
F_0 = lambda r: (1/(np.sqrt(2*np.pi*vza)))*np.exp(-((r-X_0)**2)/(2*vza))
PC_0 = quad(F_0,y[0],g)[0]
F_1 = lambda r: (1/(np.sqrt(2*np.pi*vza)))*np.exp(-((r-X_1)**2)/(2*vza))
PC_1 = quad(F_1,g,y[-1])[0]
"""
# La probabilidad correcta en el caso MAP
PC = P_0*PC_0 + P_1*PC_1
# La probabilidad de error en el caso MAP
PE = 1 - PC
print('P_e para el detector MAP: {:.2E}'.format(PE))
# Encontrar la frontera de la región de decisión g con el detector ML
indexUmbral = np.where(f_1 > f_0)[0][0]
g = r[indexUmbral]
""" Alternativamente
g = y[np.where(P_1*f_1 > P_0*f_0)][0]
Primer valor (índice [0]) en el que P1f1>P0f0
"""
print('Umbral ML, g: {:.2f}'.format(g))
# Calcular las integrales de manera aproximada
PC_0 = np.sum(f_0[:indexUmbral])*paso
PC_1 = np.sum(f_1[indexUmbral:])*paso
"""Alternativamente
from scipy.integrate import quad
F_0 = lambda y: (1/(np.sqrt(2*np.pi*vza)))*np.exp(-((y-X_0)**2)/(2*vza))
PC_0 = quad(F_0,y[0],g)[0]
F_1 = lambda y: (1/(np.sqrt(2*np.pi*vza)))*np.exp(-((y-X_1)**2)/(2*vza))
PC_1 = quad(F_1,g,y[-1])[0]
"""
# La probabilidad correcta en el caso ML
PC = P_0*PC_0 + P_1*PC_1
# La probabilidad de error en el caso ML
PE = 1 - PC
print('P_e para el detector ML: {:.2E}'.format(PE))
Cálculo de la probabilidad de error con ruido gaussiano y caso binario Umbral MAP, g: -0.27 P_e para el detector MAP: 1.92E-02 Umbral ML, g: 0.00 P_e para el detector ML: 2.28E-02
Ejercicio propuesto¶
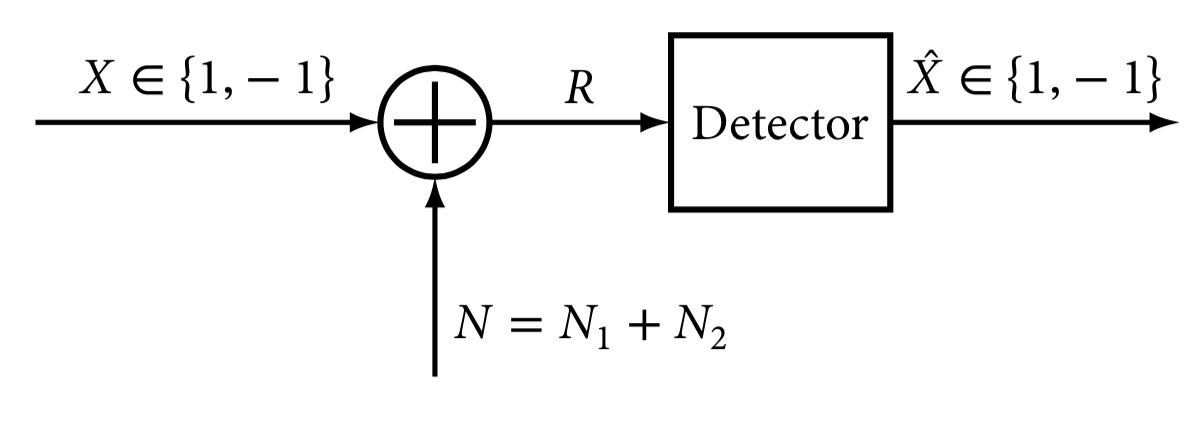
En un problema de test de hipótesis como el mostrado en la Figura 3.10, la variable aleatoria $X$ toma los valores {1, -1} con probabilidades 1/4 y 3/4 respectivamente. Se tiene que la variable aleatoria $N$ viene dada por $N = N_1 + N_2$, con $N_1$ y $N_2$ dos variables aleatorias uniformemente distribuidas entre [−1,1].
1. Generar $N_p=1e6$ muestras de la variable aleatoria $X$. Representar su función masa de probabilidad estimada.
2. Generar $N_p=1e6$ muestras de la variable aleatoria $N$. Representar su función densidad de probabilidad estimada
3. Representar las estimaciones de las funciones densidad de probabilidad condicional $f_{R|X=-1}(r|X =-1)$ y $f_{R|X=1}(r|X=1)$.
4. Representar en una misma gráfica $qf_{R|X=-1}(r|X=-1)$ y $pf_{R|X=1}(r|X=1)$, siendo $p$ y $q$ las probabilidades a priori de la variable aleatoria $X$; esto es, $p = P(X=+1)$ y $q = P(X=-1)$.
5. Encontrar experimentalmente la frontera de la región de decisión cuando el detector utiliza una regla MAP y cuando utiliza una regla ML.
6. Calcular las probabilidades $P_e(-1|Tx)$ y $P_e(+1|Tx)$ para el caso MAP y el caso ML
7. Calcular la probabilidad de error del detector cuando siga las reglas MAP y ML.
8. Proponer una estimación de estas probabilidades de forma experimental y comprobar su coincidencia (o no) con el cálculo teórico
a) A partir de las estimaciones de las funciones densidad de probabilidad.
b) A partir de conteo de muestras erróneas en el receptor
 Run in Google Colab
Run in Google Colab