Notebook

MANUAL DE LABORATORIO DE COMUNICACIONES DIGITALES: PYTHON¶

F. Javier Payán Somet, Juan José Murillo-Fuentes, José Carlos Aradillas Jaramillo
Departamento de Teoría de la Señal y Comunicaciones
Escuela Técnica Superior de Ingeniería
Universidad de Sevilla

Tema 6. Demodulador óptimo en un canal AWGN¶

Este notebook contiene código del Tema 6

Run in Google Colab

Inicialización¶

In [1]:

# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)

# Numpy ≥1.16 is required
import numpy as np
assert np.__version__ >= "1.16"

# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)

# Ignore useless warnings
import warnings
warnings.filterwarnings(action="ignore") #Ignorar warnings

Diseño experimental¶

Simulación de un canal AWGN discreto¶

Código 6.1 Salida del receptor vectorial en un canal AWGN para una PAM.

Las funciones que se describen aquí están en el fichero labcomdig.py y se definieron en temas anteriores

In [2]:

def transmisorpam(Bn,Eb,M,p,L):
    '''
    [Xn,Bn,An,phi,alfabetopam] = transmisorpam(Bn,Eb,M,p,L) 
    
    Entradas:    
     Bn = Secuencia de dígitos binarios
     Eb = Energía media por bit transmitida en Julios
     M  = Número de síímbolos del código PAM
     p  = Pulso paso de baja o paso de banda 
     L  = Número de puntos a utilizar en la representación de un símbolo
    
    Devuelve:
     Xn = la señal de información (discreta)
     Bn = La secuencia de dígitos binarios realmente transmitidos
     An = La secuencia de niveles de amplitud transmitidos
   	 phi = Pulso básico real normalizado (energía unidad)
     alfabetopam = Los niveles de amplitud asociados a cada símbolo
    '''    
    
    #Comprobación de parámetros de entrada
    p=p.squeeze()
    if len(Bn)<1 or Eb<=0 or M<2 or p@p==0 or L<1:
        raise Exception('Error: revise los parámetros de entrada')
    
    # Se obtienen en primer lugar los niveles asociado a cada símbolo ¿Cuántos bits hay en cada sí­mbolo?
    k = int(np.ceil(np.log2(M)))   
    M = 2**(k) # Se Ajusta M a una potencia de dos
    
    # El alfabeto [Ver la ecuación (4.21)] 
    alfabetopam = np.sqrt(3*Eb*np.log2(M)/(M**2-1))*(2*(np.arange(M))-M+1)
    
    # Si Bn no tiene una longitud múltiplo de k, se completa con ceros
    Nb = len(Bn)  # Número de bits a transmitir, actualizado
    Bn = Bn.squeeze().astype(int) #Comprobación de int y dimensiones   
    Bn = np.r_[Bn,np.zeros(int(k*np.ceil(Nb/k)-Nb)).astype(int)] #
    Nb = len(Bn)  # Número de bits a transmitir tras la corrección
    Ns = Nb//k # Número de símbolos a transmitir
    
    # La secuencia generada
    if M>2:
        An = alfabetopam[gray2de(np.reshape(Bn,[Ns,k]))]
    else:
        An = alfabetopam[Bn]
    
    # Comprobación de las longitudes y otros datos del pulso suministrado para 
    # hacer que el número de muestras del mismo sea efectivamente L
    Ls = len(p)
    if Ls<L:
        p = np.r_[p, np.zeros(L-Ls)]
    elif Ls>L:
        print('La duración del pulso se trunca a {} muestras'.format(str(L)))
        p = p[:L] #Debe modificarse si se quiere un pulso de más de L muestras 
    # Se normaliza la energía del pulso para obtener la base del sistema
    phi = p / np.sqrt(p@p) 
       
    # Obtención del tren de pulsos, Xn = np.kron(An,phi) ó
    Xn = np.reshape(np.reshape(An,[Ns,1])*phi,[Ns*L,]) #Debe modificarse si se quiere un pulso de más de L muestras
    return [Xn,Bn,An,phi,alfabetopam]

Se necesita la siguiente función, del notebook anterior:

In [3]:

def gray2de(b):
    '''
    Convierte cada columna de la matriz formada por dígitos binarios b en un vector
        fila de los valores decimales correspondientes, aplicando codificación de Gray.
    '''
    if not isinstance(b, (np.ndarray, list, tuple)):  # se comprueba que no sea np.array, lista o tupla
       raise Exception('Error: la entrada no es un array, lista o tupla')
    b = np.array(b)    # Esto es para que admita también listas y tuplas
    c = np.zeros_like(b); c[:,0] = b[:,0]
    for i in range(1,np.shape(b)[1]):
        c[:,i] = np.logical_xor(c[:,i-1], b[:,i])
    c = np.fliplr(c) # Convierte los bits menos significativos en los más significativos
    #Comprueba un caso especial.
    [n,m] = np.shape(c) 
    if np.min([m,n]) < 1:
        d = []
        return
    d = c @ 2**np.arange(m)
    return d 

y, más adelante para la demodulación de una señal QAM,

In [4]:

def split(Bn, M1, M2):
    '''
    Entradas
        Bn = una secuencia de símbolos binarios
        M1 = nº de símbolos de la componente en fase
        M2 = nº de símbolos de la componente en cuadratura    
    Salida     
        Bn = una secuencia de símbolos binarios
        M1 = nº de símbolos de la componente en fase
        M2 = nº de símbolos de la componente en cuadratura
    '''
    
    k1 = int(np.log2(M1))
    k2 = int(np.log2(M2))
    k = k1 + k2
    
    #Longitud de la secuencia
    Nb = len(Bn)
    
    #Una matriz con Ns=Nb/k filas formadas por los k bits
    W = np.reshape(Bn,[int(Nb/k),k])
    
    #Extrae la submatriz formada por los k1 primeros bits y pone una fila tras otra
    BnI = np.reshape(W[:,:k1],[k1*int(Nb/k)])
    
    #Extrae la submatriz formada por los k2 bits restantes y pone una fila tras otra
    BnQ = np.reshape(W[:,k1:],[k2*int(Nb/k)]) 
    
    return BnI, BnQ

Código 6.1 Salida del receptor vectorial en un canal AWGN para una PAM.

In [5]:

np.random.seed(76) #To get same results

#%% Transmisor
M = 8 #Tamaño de la constalación
Eb = 4 # Energía por bit transmitida
L = 4 #N. de muestras por símbolo
Nb = 10**4 #N. de bits a transmitir
p = np.ones(L)
Bn = np.random.randint(2, size = Nb)
[Xn, Bn, An, phi, alfabeto] = transmisorpam(Bn,Eb,M,p,L)

#%% Canal 
SNRdb = 0
SNR = 10**(SNRdb/10) #paso a unidades naturales
varzn = Eb/(2*SNR) #Cálculo de la varianza del ruido
Wn = np.sqrt(varzn)*np.random.randn(len(Xn)) #Muestras de ruido, del canal
rn = Xn + Wn  #Salida del canal, entrada al receptor vectorial

#%% Receptor Vectorial
M = len(alfabeto)  #Símbolos de la constelación M-PAM
Nb = len(Bn)  #Número de bits transmitidos
Ns = int(Nb/np.log2(M))   #Nçumero d esímbolos transmitidos

# Mediante filtro adaptado
hr = np.flipud(phi)
yn = np.convolve(hr, rn, 'valid')
r = yn[np.arange(0,Ns*L,L)]  #Salida del receptor vectorial

# Mediante correlador
r = np.reshape(rn,[Ns,L]) @ phi  #Salida del receptor vectorial

#%% Representación de resultados
plt.figure(1, figsize=(10,6))
plt.stem(r[:30],linefmt='b-',markerfmt='bo',basefmt='k-',use_line_collection = True)
plt.xlabel('n')
markerline, stemlines, baseline = plt.stem(An[:30],linefmt='r-',markerfmt='r_',basefmt='k-',use_line_collection = True)
plt.setp(stemlines, 'linewidth', 3)
plt.legend(['r','An'])

Out[5]:

<matplotlib.legend.Legend at 0x1209e0cd0>

Constelación recibida¶

Constelación mediante un banco de correladores¶

Rescatamos la siguiente función, al igual que las anteriores contenida en labdomdig.py

In [6]:

def transmisorqam(Bn, Eb, M1, M2, p1, p2, L): 
    '''
    [Xn,BnI,BnQ,AnI,AnQ,AI,AQ,phi1,phi2] = transmisorqam(Bn, Eb, M1, M2,p1,p2,L)
    
    Entradas:
     Bn = Secuencia de dígitos binarios
     Eb = Energía media por bit transmitida en Julios
     M1 = Nº de símbolos de la componente en fase
     M2 = Nº de símbolos de la componente en cuadratura
     p1 = Pulso real de la componente en fase
     p2 = Pulso real de la componente en cuadratura
     L = Nº de puntos que vamos a utilizar en la representación un símbolo
        
    Devuelve:
     Xn = la señal de información digital
     BnI = Bits transmitidos por la componente en fase
     BnQ = Bits transmitidos por la componente en cuadratura
     AnI = Niveles de amplitud transmitidos por la componente en fase
     AnQ = Niveles de amplitud transmitidos por la componente en cuadratura 
     AI = Niveles de amplitud usados en la componente en fase
     AQ = Niveles de amplitud usados en la componente en cuadratura
     phi1 = Pulso básico normalizado (energí­a unidad) de la componente en fase
     phi2 = Pulso básico normalizado (energí­a unidad) de la componente en cuadratura 
    '''
    #Comprobación de parámetros de entrada
    p1 = p1.squeeze()
    p2 = p2.squeeze()
    if len(Bn)<1 or Eb<=0 or M1<2 or M2<2  or p1@p1==0 or p2@p2==0 or L<1:
       raise Exception('Error: revise los parámetros de entrada')    
       
    #Definiciones
    eps = np.finfo(float).eps # por debajo de este valor se considera cero
    
    #Comprobación de los pulsos básicos
    Ls1 = len(p1)
    Ls2 = len(p2)
    if Ls1<L:
        p1 = np.r_[p1, np.zeros(int(L-Ls1))]
    elif Ls1>L:
        p1 = p1[:L]
        print('La duración del pulso se trunca a {} muestras'.format(str(L)))
    if Ls2<L:
        p2 = np.r_[p2, np.zeros(int(L-Ls2))]
    elif Ls1>L:
        p2 = p2[:L]
        print('La duración del pulso se trunca a {} muestras'.format(str(L)))       

    #Normalicemos las energías de los pulsos
    phi1 = 1/np.sqrt(p1@p1)*p1
    phi2 = 1/np.sqrt(p2@p2)*p2
    
    #Comprobemos la ortogonalidad
    if np.abs(phi1@phi2) >= 1e2*eps:
        raise Exception('Bases no ortogonales, no es posible realizar la transmisión')
    
    #Ajuste de los parámetros   
    k1 = int(np.ceil(np.log2(M1))) #Número de bits de la componente en fase
    M1 = 2**(k1) #Valor de M1 tras la corrección
    k2 = int(np.ceil(np.log2(M2))) #Número de bist de la componente en cuadratura M2 = 2**(k2) #Valor de M2 tras la corrección
    k = k1 + k2 #Número de bits en cada símbolo QAM
    Nb = len(Bn); Bn = Bn.squeeze().astype(int) #Comprobación de int y dimensiones
    Bn = np.r_[Bn,np.zeros(int(k*np.ceil(Nb/k)-Nb)).astype(int)]    
    
    #Obtención de la mitad de la distancia mínima entre símbolos para Eb dada
    A = np.sqrt(3*Eb*np.log2(M1*M2)/(M1**2+M2**2-2))
    
    #El alfabeto con los niveles
    AI = A * (2*np.arange(M1)-M1+1)
    AQ = A * (2*np.arange(M2)-M2+1)
    
    #Separación de la secuencia de bits en las secuencias de las componentes en fase y cuadratura
    BnI,BnQ = split(Bn,M1,M2)
    NbI = len(BnI)
    NbQ = len(BnQ)
    
    #Obtención de la secuencia de símbolos de las componentes en fase y cuadratura
    if M1>2:
        AnI = AI[gray2de(np.reshape(BnI,[int(NbI/k1),k1]))] 
    else:
        AnI = AI[BnI]
    if M2>2:
        AnQ = AQ[gray2de(np.reshape(BnQ,[int(NbQ/k2),k2]))]
    else:
        AnQ = AQ[BnQ]
    Ns = len(AnI)    
    
    #Las componentes en fase, cuadratura y total de la señal discreta a transmitir
    XnI=np.reshape(np.reshape(AnI,[Ns,1])*phi1,[Ns*L,]) #ó XnI=np.kron(AnI, phi1);
    XnQ=np.reshape(np.reshape(AnQ,[Ns,1])*phi2,[Ns*L,]) #ó XnQ=np.kron(AnQ, phi2);
    Xn = XnI+XnQ;
    return Xn, BnI, BnQ, AnI, AnQ, AI, AQ, phi1, phi2 

Código 6.2 Constelación de un sistema QAM rectangular paso de baja.

In [7]:

# Datos
Bn = np.random.randint(2, size=10**4)
Eb = 2
L = 4
M1 = 4
M2 = 4

#%% Definición de los pulsos básicos
p1 = np.r_[np.ones(int(L/2)), np.zeros(int(L/2))] 
p2 = np.r_[np.zeros(int(L/2)), np.ones(int(L/2))]

#%% Transmisor: obtención de la señal QAM
[Xn,BnI,BnQ,AnI,AnQ,AI,AQ,phi1,phi2] = transmisorqam(Bn,Eb,M1,M2,p1,p2,L)

#%% Obtengamos los parámetros necesarios para la representación tras las posibles modificaciones
L = len(phi1)                       #Número de muestras por sí­mbolo
Ns = int((len(BnI)+len(BnQ))/(np.log2(len(AI)*len(AQ))))	#Nº de sí­mbolos transmitidos

#%% Receptor vectorial: obtención de las secuencias de niveles transmitidos
#El canal es perfecto, a su salida se tiene una copia de la entrada
#sn = np.dot(np.reshape(Xn,[Ns,L]),np.c_[phi1,phi2])
sn = np.reshape(Xn,[Ns,L]) @ np.c_[phi1,phi2]
sn1 = sn[:,0]
sn2 = sn[:,1]

#%% Extraemos la constellación de los valores recibidos
s1 = np.unique(np.single(sn1))  #Valores distintos encontrados en An1
xmax = max(s1)+max(s1)/10+0.5
xmin = -(abs(min(s1))+abs(min(s1))/10)-0.5

s2 = np.unique(np.single(sn2))  #Valores distintos encontrados en An2
ymax = np.max(s2)+np.max(s2)/10+0.5
ymin = -(np.abs(np.min(s2))+np.abs(np.min(s2))/10)-0.5

#%% Se representa la constellación
plt.figure(61,figsize=(6,6))
# Representa los ejes
plt.plot([xmin,xmax],[0,0],'b-')
plt.plot([0,0],[ymin,ymax],'b-')
#Representa la constelación
for ii in range(len(s1)):
    for jj in range(len(s2)):
        plt.plot(s1[ii],s2[jj], 'r*')
plt.axis('square')
plt.grid()

Constelación mediante filtros adaptados¶

Usamos la función ya definida en el tema anterior

In [8]:

def transmisorpsk(Bn,Eb,M,p1,p2,L): 
    '''
    [Xn,Bn,An,phi1,phi2,alfabeto] = transmisorpsk(Bn,Eb,M,p1,p2,L)
   
    Entradas:
    Bn = Secuencia de dígitos binarios
    Eb = Energía media por bit transmitida en Julios
    M = Número de símbolos del código PSK
    p1 = Pulso real de la componente en fase
    p2 = Pulso real de la componente en cuadratura
    L = Número de puntos que se utilizará en la representación de un símbolo
    
    Devuelve:
    Xn = la señal de información discreta
    Bn = La secuencia de dígitos binarios realmente transmitidos
    An = La secuencia de símbolos complejos transmitidos
    phi1 = Pulso básico real normalizado (energí­a unidad) de la componente en fase
    phi2 = Pulso básico real normalizado (energí­a unidad) de la componente en cuadratura
    alfabeto = El alfabeto utilizado asociado a cada símbolo transmitido
    '''
    #Comprobación de parámetros de entrada
    p1 = p1.squeeze(); p2 = p2.squeeze()
    if len(Bn)<1 or Eb<=0 or M<2 or p1@p1==0 or p2@p2==0 or L<1:
       raise Exception('Error: revise los parámetros de entrada')
        
    #Definiciones
    eps = np.finfo(float).eps # por debajo de este valor se considera cero
      
    # Comprobación de las longitudes y otros datos de los pulsos de llamada
    Ls1 = len(p1)
    Ls2 = len(p2)
    if Ls1==0 or Ls2==0:
        print('No es posible realizar la transmisión') 
        return
   
    if Ls1<L:
        p1 = np.r_[p1, np.zeros(int(L-Ls1))]
    elif Ls1>L:
        p1 = p1[:L]
        print('La duración del pulso se trunca a {} muestras'.format(str(L)))
    if Ls2<L:
        p2 = np.r_[p2, np.zeros(int(L-Ls2))]
    elif Ls2>L:
        p2 = p2[:L]
        print('La duración del pulso se trunca a {} muestras'.format(str(L)))       
       
    # Se comprueba la ortogonalidad
    if abs(p1@p2) >= 1e0*eps*10:
        print('No es posible realizar la transmisión') 
        return
       
    # Se normalizan las energías de los pulsos
    phi1 = p1 / np.sqrt(p1@p1) 
    phi2 = p2 / np.sqrt(p2@p2)  
    # Se genera el pulso complejo [Ver la ecuación (5.25)]
    phi = phi1 - 1j*phi2
   
    # Obtención de los niveles asociados a cada símbolo: alfabeto
    # Número de bits por símbolo
    k = int(np.ceil(np.log2(M)))
    # Se ajusta M a una potencia de dos
    M = 2**(k)
    # El alfabeto [Ver la ecuación (5.24)]
    alfabeto = np.sqrt(Eb*k)*np.exp(1j*2*np.pi*np.arange(M)/M) #empieza en 0
   
    # Si la longitud de Bn no es múltiplo de k, se completa con ceros
    Nb = len(Bn) 
    Bn = np.r_[Bn,np.zeros(int(k*np.ceil(Nb/k)-Nb)).astype(int)] #
   
    # Número de bits y símbolos que vamos a transmitir
    Nb = len(Bn) # Número de bits que vamos a transmitir tras la corrección 
    Ns = int(Nb/k)

    # La secuencia generada
    if M>2:
         An = alfabeto[gray2de(np.reshape(Bn,[Ns,k]))]
    else:
        An = alfabeto[Bn]
    
    # Obtención del tren de pulsos,    Xn = np.real(np.kron(An, phi))  ó
    Xn = np.real(np.reshape(np.reshape(An,[Ns,1])*phi,[Ns*L,]))
    return [Xn, Bn, An, phi1, phi2, alfabeto] 

Código 6.3 Constelación de un sistema M-PSK paso de baja mediante filtros adaptados.

In [9]:

#%% Datos
Bn = np.random.randint(2, size=10**4)
Eb = 4/3
L = 8
M = 8

#%% Definición de los pulsos básicos
p1 = np.r_[np.ones(int(L/2)), np.zeros(int(L/2))] 
p2 = np.r_[np.zeros(int(L/2)), np.ones(int(L/2))] 

#%% Transmisor: Generación de la señal M-PSK
[Xn,Bn,An,phi1,phi2,alfabeto] = transmisorpsk(Bn,Eb,M,p1, p2, L);
k = np.log2(len(alfabeto))
L = len(phi1)     #Número de muestras por símbolo
Ns = int(len(Bn)/k)  #Nº de símbolos transmitidos

#%% Receptor Vectorial con filtros adaptados
hr1 = np.flipud(phi1)
hr2 = np.flipud(phi2)

yn1 = np.convolve(hr1,Xn, 'valid')
yn2 = np.convolve(hr2,Xn, 'valid')

# Señal de salida
sn1 = yn1[np.arange(0,Ns*L,L)]          
sn2 = yn2[np.arange(0,Ns*L,L)]   
      
#%% Representación: 
# Obtiene valores máximos y mínimos para la representación
xmax = max(sn1) + max(sn1)/10 + 0.5
xmin = -(abs(min(sn1)) + abs(min(sn1))/10) - 0.5
ymax = max(sn2) + max(sn2)/10 + 0.5
ymin = -(abs(np.min(sn2))+abs(min(sn2))/10) - 0.5

plt.figure(62,figsize=(6,6))
# Pinta los ejes
plt.plot([xmin,xmax],[0,0],'b-')
#hold
plt.plot([0,0],[ymin,ymax],'b-')

# Representa
Nmax = int(min(64,len(Bn)/k))
plt.plot(sn1[:Nmax],sn2[:Nmax], 'r*')
plt.axis('square')
plt.grid()

Scattering plot del vector de observación¶

Código 6.4 Scattering plot de un sistema QAM rectangular.

In [10]:

# Datos
Bn = np.random.randint(2, size=10**3)
Eb = 4
L = 4
M1 = 2
M2 = 2

#%% Transmisor. Definición de los pulsos básicos
p1 = np.r_[np.ones(int(L/2)), np.zeros(int(L/2))] 
p2 = np.r_[np.zeros(int(L/2)), np.ones(int(L/2))] 

# Obtención de la señal QAM
[Xn,BnI,BnQ,AnI,AnQ,AI,AQ,phi1,phi2] = transmisorqam(Bn,Eb,M1,M2,p1,p2,L)

# Obtengamos los parámetros necesarios para la representación tras las posibles modificaciones
L = len(phi1);                       #Número de muestras por sí­mbolo
Ns = int((len(BnI)+len(BnQ))/(np.log2(len(AI)*len(AQ))))  #Nº de sí­mbolos transmitidos

#%% Constelación en ausencia de ruido
sn = np.dot(np.reshape(Xn,[Ns,L]),np.c_[phi1,phi2])
sn1 = sn[:,0]
sn2 = sn[:,1]

# Obtiene los valores únicos
sx = np.unique(np.single(sn1))
xmax = max(sx)+max(sx)/10+0.5
xmin = -(abs(min(sx))+abs(min(sx))/10)-0.5

sy = np.unique(np.single(sn2))
ymax = max(sy)+max(sy)/10+0.5
ymin = -(abs(min(sy))+abs(min(sy))/10)-0.5

#%% Constellación (scattering) recibida para diversos valores de SNRdb
plt.figure(63, figsize=(15,15))
for SNRdB in range(9):  #SNR = 0,1,2,...,8  dB
    plt.subplot(3,3,SNRdB+1)
    # Representa los ejes
    plt.plot([xmin,xmax],[0,0],'b-')
    
    plt.plot([0,0],[ymin,ymax],'b-')
    plt.grid(), plt.axis('square')
    # Se obtiene varianza del ruido del canal
    
    SNR = 10**(SNRdB/10)  #SNR en unidades naturales
    varzn = Eb/(2*SNR)
    # Se obtienen muestras de ruido a sumar en el canal, se suman y se recuperan
    Wn = np.sqrt(varzn)*np.random.randn(np.size(Xn))
    r = np.reshape(Xn+Wn,[Ns,L]) @ np.c_[phi1,phi2] #Salida Rx Vectorial
    plt.plot(r[:,0], r[:,1], '.b')
    plt.axis([-5, 5, -5, 5])
    # Representa los valores obtenidos a la salida del receptor vectorial
    for ii in range(len(sx)):
        for jj in range(len(sy)):
            plt.plot(sx[ii],sy[jj], 'ro'); 
            plt.xlabel('$E_b/N_0=$' + str(SNRdB) + 'dB')
plt.tight_layout
plt.show()

Ejercicio propuesto¶

Se desea generar una señal PAM para lo cual se utiliza la función transmisorpam diseñada en el Capítulo 4. Las señales transmitidas vienen dadas por:

$$ si(t) = A_i\phi(t), i = 1, . . . ,M $$

dónde $A_i \in {−7C,−5C,−3C,−C, C, 3C, 5C, 7C}$ y $\phi(t)$ es un pulso de energía unidad proporcional al pulso mostrado en la Figura 6.18.

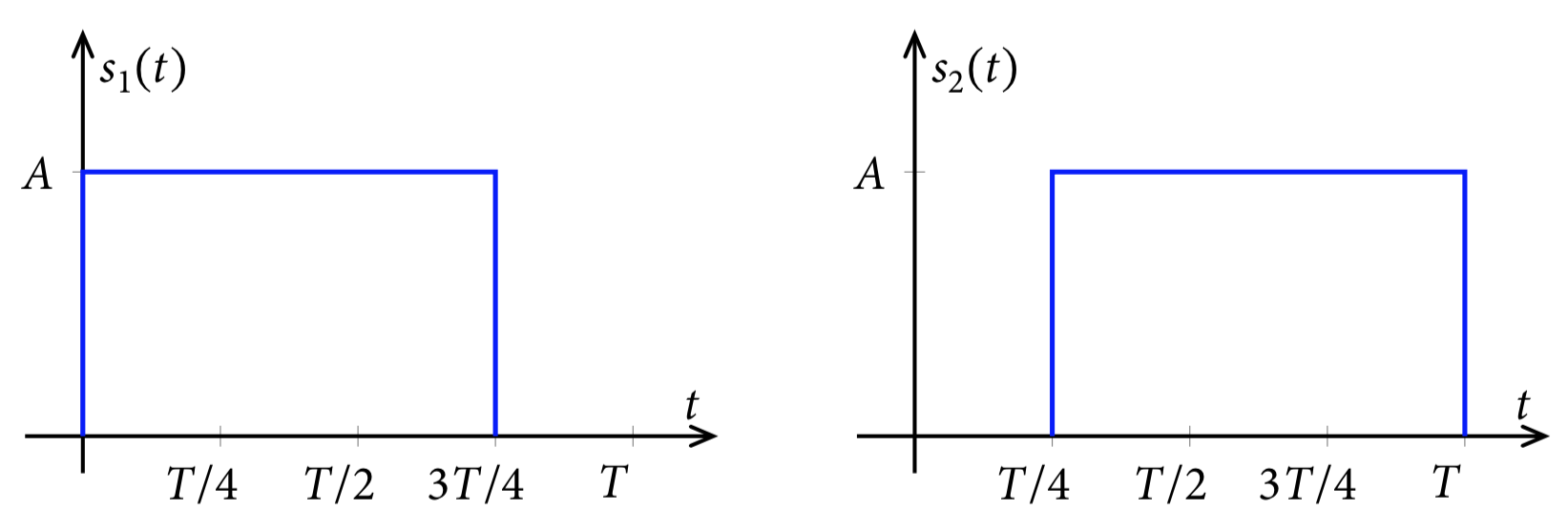
1. Determinar C para que la energía por bit transmitida sea 7/4 J.

In [ ]:

Utilizando la función transmisorpam, escribir el código que permite obtener la señal discreta transmitida cuando:

a) La secuencia transmitida está formada por la conversión de decimal a binario de los cuatro primeros dígitos del DNI del lector.

b) L = 8.

c) El pulso básico de duración T es el mostrado en la Figura 6.18.

In [ ]:

3. Representar la versión discreta de la señal transmitida.

In [ ]:

4. Obtener la constelación de las señales transmitidas y representarla de manera similar a las mostradas en las figuras 6.13 y 6.14. Para ello modificar el código anterior para que se transmita un total de $N_b=10^5$ bits.

In [ ]:

5. Si se supone que la señal se transmite en un canal AWGN, diseñar un demodulador y obtener y representar la función densidad de probabilidad del vector de observación cuando la relación SNR se encuentra entre 4 dB y 18 dB, con un incremento de 2 dB.

In [ ]: