Convolutional Neural Nets¶
This type of neural nets are predominantly (and heavily) used in image processing. This lesson is on the CIFAR-10 dataset.
Useful terms:¶
- Conv2D
- MaxPool2D
- BatchNormalization
Further Readings:¶
https://ujjwalkarn.me/2016/08/11/intuitive-explanation-convnets/
In [1]:
!pip install tqdm
Requirement already satisfied: tqdm in /root/miniconda3/lib/python3.6/site-packages
In [1]:
import numpy as np
import matplotlib.pyplot as plt
from urllib.request import urlretrieve
from os.path import isfile, isdir
from tqdm import tqdm
import tarfile
import pickle
from keras.models import Sequential
from keras.layers import Dense, Activation, Conv2D, MaxPool2D, Flatten, BatchNormalization, Dropout
%matplotlib inline
Using Theano backend.
In [3]:
cifar10_dataset_folder_path = 'cifar-10-batches-py'
class DLProgress(tqdm):
last_block = 0
def hook(self, block_num=1, block_size=1, total_size=None):
self.total = total_size
self.update((block_num - self.last_block) * block_size)
self.last_block = block_num
if not isfile('cifar-10-python.tar.gz'):
with DLProgress(unit='B', unit_scale=True, miniters=1, desc='CIFAR-10 Dataset') as pbar:
urlretrieve(
'https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz',
'cifar-10-python.tar.gz',
pbar.hook)
if not isdir(cifar10_dataset_folder_path):
with tarfile.open('cifar-10-python.tar.gz') as tar:
tar.extractall()
tar.close()
label_dict = dict(zip(range(10),
['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']))
width = height = 32
channels = 3
train_examples = 50000
# Get the test set
with open(cifar10_dataset_folder_path + '/test_batch', mode='rb') as file:
batch = pickle.load(file, encoding='latin1')
test_x = batch['data'].reshape((len(batch['data']), 3, 32, 32)).transpose(0, 2, 3, 1)/255
test_y = batch['labels']
In [4]:
def get_batch(batch_size):
n_batches = 5
while(1):
for batch_id in range(1, n_batches + 1):
with open(cifar10_dataset_folder_path + '/data_batch_' + str(batch_id), mode='rb') as file:
batch = pickle.load(file, encoding='latin1')
features = batch['data'].reshape((len(batch['data']), 3, 32, 32)).transpose(0, 2, 3, 1)
labels = batch['labels']
for start in range(0, len(features), batch_size):
end = min(start + batch_size, len(features))
yield features[start:end]/255, np.array(labels[start:end])
In [5]:
x, y = next(get_batch(5))
for im, label in zip(x,y):
plt.imshow(im)
plt.title(label_dict[label])
plt.show()
Basic logistic multiclass classification:¶
In [6]:
batch_size = 1000
gen = get_batch(batch_size)
x_train, y_train = next(gen)
In [7]:
from sklearn.linear_model import LogisticRegression
logistic = LogisticRegression()
logistic.fit(x_train.reshape(batch_size,-1), y_train)
Out[7]:
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0, warm_start=False)
In [8]:
y_pred = logistic.predict(test_x.reshape(len(test_x), -1))
y_pred[:10]
Out[8]:
array([6, 1, 8, 0, 4, 3, 3, 6, 1, 1])
Predicting the probabilities for the first 3 images:
In [9]:
logistic.predict_proba(test_x[:3].reshape(3,-1))
Out[9]:
array([[ 5.11780589e-02, 5.22601998e-02, 1.55926385e-01,
1.91240503e-01, 3.91236477e-04, 1.54297967e-01,
2.80945273e-01, 1.19926488e-06, 1.13659809e-01,
9.93687013e-05],
[ 2.16303715e-02, 7.31044039e-01, 2.69961983e-03,
1.05058501e-01, 4.19521439e-04, 4.01069801e-03,
7.30693763e-06, 2.05908231e-04, 2.05482815e-02,
1.14375752e-01],
[ 6.08332707e-02, 8.16219690e-02, 7.55828475e-03,
1.26261683e-01, 2.92891682e-02, 9.79890820e-03,
7.44308146e-03, 4.27092877e-03, 6.19882712e-01,
5.30399941e-02]])
Accuracy of the predictions:
In [10]:
np.count_nonzero(y_pred == test_y)/len(test_y)
Out[10]:
0.275
The number of parameters for a fully connected network:
In [11]:
32*32*3*10
Out[11]:
30720
Keras Multilayered Perceptron (Neural Net)¶
In [12]:
def get_batch(batch_size):
n_batches = 5
while(1):
for batch_id in range(1, n_batches + 1):
with open(cifar10_dataset_folder_path + '/data_batch_' + str(batch_id), mode='rb') as file:
batch = pickle.load(file, encoding='latin1')
features = batch['data'].reshape((len(batch['data']), 3, 32, 32)).transpose(0, 2, 3, 1)
labels = batch['labels']
for start in range(0, len(features), batch_size):
end = min(start + batch_size, len(features))
x = features[start:end]/255
y = labels[start:end]
yield x.reshape(len(x),-1), np.array(y)
It is important to note that when we do classification problems we use the Categorical Crossentropy Loss. When its only two classes we can use Logistic Loss (Binary Crossentropy Loss). Finally for regression problems we use Mean Squared Error.
The Cross Entropy loss is defined as: $$\mathcal{L} = -\frac{1}{N}\sum_i \mathcal{I}(y_i=1)\log(p_{i1})+\mathcal{I}(y_i=2)\log(1-p_{i2})+\cdots++\mathcal{I}(y_i=K)\log(1-p_{iK})$$ where $N$ is the number of training instances, $K$ is the number of classes and $p_{ik}$ is the probability that instance $i$ belongs to $k$.
Softmax takes a $D$ dimensional vector and squeezes them through a function such that we have $D$ outputs whos values are positive and sums to one. $$ \text{softmax}(\mathbf{y})_d = \frac{\exp(-y_d)}{\exp(-y_1)+...+\exp(-y_D)} $$
1 Hidden Layer¶
In [2]:
Dense?
In [13]:
model = Sequential()
# TODO: Do a 'Normal' 1 Hidden layer NN (Refresher https://keras.io/#getting-started-30-seconds-to-keras)
# Note that the number of inputs is width*height*channels
# The last layer is a softmax layer (it outputs the probability of the ten classes)
# The loss function is 'sparse_categorical_crossentropy' and use either 'adagrad' or 'adadelta' as the optimizer
model.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_1 (Dense) (None, 100) 307300 _________________________________________________________________ dense_2 (Dense) (None, 10) 1010 ================================================================= Total params: 308,310.0 Trainable params: 308,310 Non-trainable params: 0.0 _________________________________________________________________
In [14]:
batch_size = 256
model.fit_generator(get_batch(batch_size=batch_size), train_examples//batch_size, epochs=1)
Epoch 1/1 195/195 [==============================] - 3s - loss: 2.0330
Out[14]:
<keras.callbacks.History at 0x7faada64e710>
In [15]:
y_pred = model.predict_classes(test_x.reshape(len(test_x),-1))
np.count_nonzero(y_pred == test_y)/len(test_y)
9152/10000 [==========================>...] - ETA: 0s
Out[15]:
0.3337
Convolution Neural Networks (CNN)¶
** Points to note **
- One CNN, connected to one node above is simply a Dense layer with most weights set to zero.
- The same CNN, connected to multiple nodes is weight tying/ sharing.
Consider the following convolution mask:
In [16]:
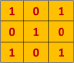
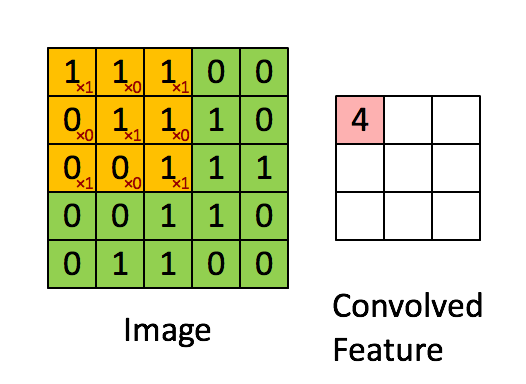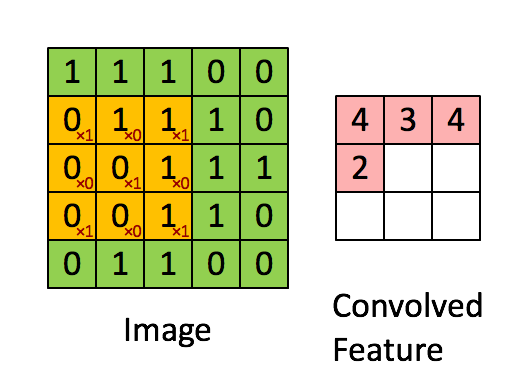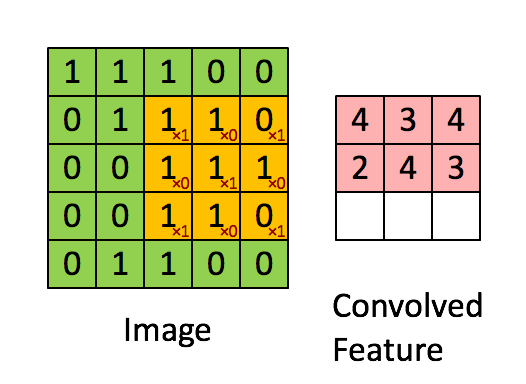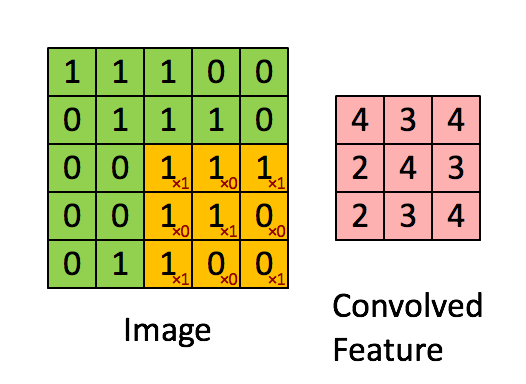
def get_batch(batch_size):
n_batches = 5
while(1):
for batch_id in range(1, n_batches + 1):
with open(cifar10_dataset_folder_path + '/data_batch_' + str(batch_id), mode='rb') as file:
batch = pickle.load(file, encoding='latin1')
features = batch['data'].reshape((len(batch['data']), 3, 32, 32)).transpose(0, 2, 3, 1)
labels = batch['labels']
for start in range(0, len(features), batch_size):
end = min(start + batch_size, len(features))
x = features[start:end]/255
y = labels[start:end]
yield x, np.array(y)
Using the max pooling layer:¶
In [7]:
Conv2D?
In [ ]:
MaxPool2D?
In [14]:
model = Sequential()
# TODO: Get 3 layers of Conv2D followed by MaxPool2D
# The first layer requires input_shape = (width,height,channels)
# Set activation='relu' in all layers and padding='same', Maxpool does not have an activation
# All you need to specify is the kernel_size and filters parameters
# As a thumb rule the number of filters double. eg. choose 4, 8, 16 for the 3 layers
model.add(Flatten())
model.add(Dense(10, activation='softmax'))
# Note: You so not apply dropout on final layer.
model.compile(optimizer='adadelta', loss='sparse_categorical_crossentropy')
In [15]:
model.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_4 (Conv2D) (None, 32, 32, 8) 224 _________________________________________________________________ max_pooling2d_4 (MaxPooling2 (None, 16, 16, 8) 0 _________________________________________________________________ conv2d_5 (Conv2D) (None, 16, 16, 16) 1168 _________________________________________________________________ max_pooling2d_5 (MaxPooling2 (None, 8, 8, 16) 0 _________________________________________________________________ conv2d_6 (Conv2D) (None, 8, 8, 32) 4640 _________________________________________________________________ max_pooling2d_6 (MaxPooling2 (None, 4, 4, 32) 0 _________________________________________________________________ flatten_2 (Flatten) (None, 512) 0 _________________________________________________________________ dense_2 (Dense) (None, 10) 5130 ================================================================= Total params: 11,162.0 Trainable params: 11,162.0 Non-trainable params: 0.0 _________________________________________________________________
In [ ]:
32*32*3
In [5]:
3*3*3*8+8
Out[5]:
224
In [7]:
3*3*8*16+16
Out[7]:
1168
In [16]:
batch_size = 256
model.fit_generator(get_batch(batch_size=batch_size), train_examples//batch_size, epochs=5)
Epoch 1/5 195/195 [==============================] - 28s - loss: 2.0986 Epoch 2/5 195/195 [==============================] - 29s - loss: 1.7812 Epoch 3/5 195/195 [==============================] - 29s - loss: 1.6117 Epoch 4/5 195/195 [==============================] - 29s - loss: 1.5217 Epoch 5/5 195/195 [==============================] - 33s - loss: 1.4660
Out[16]:
<keras.callbacks.History at 0x7fa693789668>
In [17]:
y_pred = model.predict_classes(test_x)
np.count_nonzero(y_pred == test_y)/len(test_y)
9792/10000 [============================>.] - ETA: 0s
Out[17]:
0.489
In [18]:
plt.figure(figsize=(12,12))
idx = np.random.choice(len(test_x),5,replace=False)
p = model.predict(test_x[idx])
for i in range(len(idx)):
plt.subplot(5,2,2*i+1)
plt.imshow(test_x[idx[i]])
plt.title(label_dict[test_y[idx[i]]])
# plt.show()
pred_label = np.argsort(-p[i])[:3]
pred_prob = [p[i][l] for l in pred_label]
pred_label = [label_dict[l] for l in pred_label]
plt.subplot(5,2,2*i+2)
plt.bar(range(3),pred_prob)
plt.xticks(range(3), pred_label)
# plt.show()
plt.show()
Batch Normalization¶
Batch Normalization makes the output of multiplying by weights 0 mean and variance of one before passing through an activation layer. This makes sure that the gradients are neither large or too small. Making the learning process faster.
In [3]:
BatchNormalization?
In [36]:
model = Sequential()
model.add(Conv2D(8, kernel_size=(3,3), padding='same', input_shape = (width,height,channels)))
model.add(Activation('relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Conv2D(16, kernel_size=(3,3), padding='same'))
# TODO: add a BatchNormalization() layer
model.add(Activation('relu'))
# TODO: add a MaxPool2D layer
# TODO: Add another set of Conv2D followed by BatchNormalization, followed by relu activation, followed by maxpool (4 lines of code)
# TODO: flatten the layer
# TODO: Add the last softmax layer
model.compile(optimizer='adadelta', loss='sparse_categorical_crossentropy', metrics = ['accuracy'])
In [37]:
model.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_22 (Conv2D) (None, 32, 32, 8) 224 _________________________________________________________________ activation_7 (Activation) (None, 32, 32, 8) 0 _________________________________________________________________ max_pooling2d_22 (MaxPooling (None, 16, 16, 8) 0 _________________________________________________________________ conv2d_23 (Conv2D) (None, 16, 16, 16) 1168 _________________________________________________________________ activation_8 (Activation) (None, 16, 16, 16) 0 ================================================================= Total params: 1,392.0 Trainable params: 1,392.0 Non-trainable params: 0.0 _________________________________________________________________
In [32]:
batch_size = 256
model.fit_generator(get_batch(batch_size=batch_size), train_examples//batch_size, epochs=5)
Epoch 1/5 195/195 [==============================] - 38s - loss: 2.0036 - Epoch 2/5 195/195 [==============================] - 43s - loss: 1.6267 Epoch 3/5 195/195 [==============================] - 46s - loss: 1.4977 Epoch 4/5 195/195 [==============================] - 49s - loss: 1.4123 Epoch 5/5 195/195 [==============================] - 49s - loss: 1.3460
Out[32]:
<keras.callbacks.History at 0x7fa690de7a20>
In [33]:
y_pred = model.predict_classes(test_x)
np.count_nonzero(y_pred == test_y)/len(test_y)
10000/10000 [==============================] - 2s
Out[33]:
0.5076
In [34]:
plt.figure(figsize=(12,12))
idx = np.random.choice(len(test_x),5,replace=False)
p = model.predict(test_x[idx])
for i in range(len(idx)):
plt.subplot(5,2,2*i+1)
plt.imshow(test_x[idx[i]])
plt.title(label_dict[test_y[idx[i]]])
# plt.show()
pred_label = np.argsort(-p[i])[:3]
pred_prob = [p[i][l] for l in pred_label]
pred_label = [label_dict[l] for l in pred_label]
plt.subplot(5,2,2*i+2)
plt.bar(range(3),pred_prob)
plt.xticks(range(3), pred_label)
# plt.show()
plt.show()
In [ ]: