Project tips¶

So you've collected data, implemented a baseline, and have an F1 of 78%.
Now what??

Error analysis
Check for data biases
Over/under fitting
Parameter tuning

Reminder: train/validation/test splits¶

Training data
- To fit model
- May use cross-validation loop
Validation data
- To evaluate model while debugging/tuning
Testing data
- Evaluate once at the end of the project
- Best estimate of accuracy on some new, as-yet-unseen data
- be sure you are evaluating against true labels
  - e.g., not the output of some other noisy labeling algorithm

Error analysis¶

What did you get wrong and why?

Fit model on all training data
Predict on validation data
Collect and categorize errors
- false positives
- false negatives
Sort by:
- Label probability

A useful diagnostic:

Find the top 10 most wrong predictions
- I.e., probability of incorrect label is near 1
For each, print the features that are "most responsible" for decision

E.g., for logistic regression

$$ p(y \mid x) = \frac{1}{1 + e^{-x^T \theta}} $$

If true label was $-1$, but classifier predicted $+1$, sort features in descending order of $x_j * \theta_j$

Error analysis often helps designing new features.

E.g., "not good" classified as positive because $x_{\mathrm{good}} * \theta_{\mathrm{good}} >> 0$
Instead, replace feature "good" with "not_good"
- similarly for other negation words

May also discover incorrectly labeled data

Common in classification tasks in which labels are not easily defined
- E.g., is the sentence "it's not bad" positive or negative?

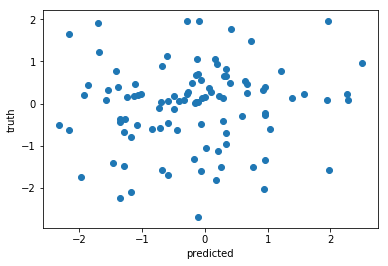
For regression, make a scatter plot - look at outliers

scatter

Inter-annotator agreement¶

How often do two human annotators give the same label to the same example?
E.g., consider two humans labeling 100 documents:

		Person 1
		Relevant	Not Relevant
Person 2	Relevant	50	20
Person 2	Not Relevant	10	20

Simple agreement: fraction of documents with matching labels. $\frac{70}{100} = 70\%$

But, how much agreement would we expect by chance?
Person 1 says Relevant $60\%$ of the time.
Person 2 says Relevant $70\%$ of the time.
Chance that they both say relevant at the same time? $60\% \times 70\% = 42\%$.
Person 1 says Not Relevant $40\%$ of the time.
Person 2 says Not Relevant $30\%$ of the time.
Chance that they both say not relevant at the same time? $40\% \times 30\% = 12\%$.
Chance that they agree on any document (both say yes or both say no): $42\% + 12\% = 54\%$

** Cohen's Kappa ** $\kappa$

Percent agreement beyond that expected by chance

$ \kappa = \frac{P(A) - P(E)}{1 - P(E)}$

$P(A)$ = simple agreement proportion
$P(E)$ = agreement proportion expected by chance

E.g., $\kappa = \frac{.7 - .54}{1 - .54} = .3478$

$k=0$ if no better than chance, $k=1$ if perfect agreement

Data biases¶

How similar is the testing data to the training data?
If you were to deploy the system to run in real-time, would the data it sees be comparable to the testing data?

Assumption that test/train data drawn from same distribution often wrong:

Label shift:

$p_{\mathrm{train}}(y) \ne p_{\mathrm{test}}(y)$

e.g., positive examples more likely in testing data
Why does this matter?

In logistic regression:

$$ p(y \mid x) = \frac{1}{1 + e^{-(x^T\theta + b)}} $$

bias term $b$ adjusts predictions to match overall $p(y)$

More bias¶

Confounders

Are there variables that predict the label that are not in the feature representation?
- e.g., some products have higher ratings than others; gender bias; location bias;
- May add additional features to model these attributes
- Or, may need to train separate classifiers for each gender/location/etc.

Temporal Bias

Do testing instances come later, chronologically, than the training instances?
- E.g., we observe that user X likes Superman II, she probably also likes Superman I
Why does this matter?
- inflates estimate of accuracy in production setting

Cross-validation splits

E.g., classifying a user/organization's tweets: does the same user appear in both training/testing
- could just be learning a user-specific classifier; won't generalize to new user
- speech recognition
Again, will inflate estimate of accuracy.

Over/under fitting¶

What is training vs validation accuracy?

If training accuracy is low, we are probably underfitting. Consider:
- adding new features
- adding combinations of existing features (e.g., ngrams, conjunctions/disjunctions)
- adding hidden units/layers
- try non-linear classifier
  - SVM, decision trees, neural nets
If training accuracy is very high (>99%), but validation accuracy is low, we are probably overfitting
- Do the opposite of above
- reduce number of features
- Regularization (L2, L1)
- Early stopping for gradient descent
- look at learning curves
- may need more training data

Parameter tuning¶

Many "hyperparameters"

regularization strength
number of gradient descent iterations
...
Be sure to tune these on the validation set, not the test set.

Grid search

Exhaustively search over all combinations
Discretize continous variables

{'C': [.01, .1, 1, 10, 100, 1000], 'n_hidden': [5, 10, 50], 'regularizer': ['l1', 'l2']},

Random search
- Define a probability distribution over each parameter
- Each iteration samples from that distribution
- Allows you to express prior knowledge over the likely best settings
- E.g.,
```
regularizer={'l1': .3, 'l2': .7}```
```

See more at http://scikit-learn.org/stable/modules/grid_search.html

While building model, may want to avoid evaluating on validation set too much
double cross-validation can be used instead
Using only the training set:
- split into $k$ (train, test) splits
- for each split ($D_{tr}, D_{te}$)
  - split $D_{tr}$ into $m$ splits
  - pick hyperparameters that maximize this nested cross-validation accuracy
  - train on all of $D_{tr}$ with those parameters

Evaluates how well your hyperparameter selection algorithm does.