Notebook

Математические методы машинного обучения. Контрольная работа

Оглавление:¶

Импортирование библиотек;
Настройка отображения
Исходая выборка;

Статистики выборки $x_1, \ldots, x_n$ :
Диаграмма Box-whiskers, определение выбросов;
Интервальный ряд c использованием формулы Стёрджеса;
График эмпирической функции распределения $F_n$ ;
Проверка распределения на нормальность:
Проверка первых 10 значений на нормальность, используя критерий Шапиро-Уилка;
$95\%$ -й доверительный интервал для неизвестной генеральной дисперсии;
$95\%$ -й доверительный интервал для неизвестного генерального среднего при условии, что:
1. Генеральные дисперсии известны;
2. Генеральные дисперсии неизвестны.
Разбиение выборки на 2 непересекающиеся группы в пропорции $55/45$ в произвольном порядке и проверка групп:
Источники

[↑] Импортирование библиотек¶

In [1]:

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

from collections import Counter
from sklearn.model_selection import train_test_split

[↑] Настройка отображения¶

In [2]:

from IPython.core.display import HTML

HTML("""
<style>
.output_png {
    display: table-cell;
    text-align: center;
    vertical-align: middle;
}
</style>
""")

Out[2]:

[↑] Исходная выборка¶

In [3]:

data = np.sort(np.array([119, 105,  85,  69, 103, 111,  92, 151,  34,  69,
                         122, 157,  91,  69, 147,  65, 100, 155,  92, 162,
                         100,  94,  95, 128,  59, 130, 122, 154,  70, 105,
                          87, 126,  83,  82, 112,  84,  69, 138,  31, 128,
                         107, 127, 111, 107,  86, 108, 103, 118,  73,  98,
                         148, 106, 142, 148, 118,  44,  92, 121,  41, 144,
                          67,  74,  61,  34, 161, 142, 113, 133,  86,  74,
                          87, 106,  69,  95,  89, 128, 123,  85, 120, 114,
                          69,  83, 102, 125,  92, 136, 110,  86,  77, 140,
                         105,  76,  54,  62,  92, 100,  74,  97,  96, 107,
                          64, 101, 103,  94, 131, 112,  85, 160, 130,  68,
                          74, 137, 109, 114,  92, 144,  64,  81, 165, 144,
                          97,  68,  60,  74,  94, 141, 162, 109,  76,  76,
                         121,  86,  98,  60, 109, 150,  55,  79,  87, 128,
                         106,  84,  57, 120, 101, 106,  90,  74,  70,  76,
                         105,  95, 101, 117,  82, 110, 118, 137, 103, 114,
                          93, 106, 110, 130,  93, 117, 139,  83,  63,  98,
                          97, 120, 101, 104,  88,  79, 108, 129, 122, 118,
                         104,  95, 110,  75,  57, 186,  97,  84, 109,  11,
                          60,  82, 100,  47,  74, 110, 149, 113, 158, 122,
                         103,  89,  64,  82, 115, 186, 200,  41, 139, 112,
                         121,  79, 129, 115, 131, 139, 135, 108, 125, 100,
                          99,  98, 160,  68, 149,  67,  94, 108, 100,  88,
                         116, 123, 100, 121, 154, 109, 103,  31,  74, 105,
                         124, 131, 125,  70,  77,  86,  79,  76,  86,  93,
                         104,  66,  45, 115,  71,  69,  66, 141,  93, 117,
                         138,  58,  58, 119, 137, 110, 140, 103,  60,  45,
                         123, 101,  75, 136,  91, 157, 107, 149, 139, 164,
                          55,  83,  63,  57,  69, 122,  62, 121, 145,  69,
                          71,  81, 119,  47,  87, 107, 107,  23, 117, 132,
                         117, 120,  75,  84, 119,  41,  78,  59, 127,  99,
                         121, 152,  92,  74,  50, 109, 108, 111, 100,  89,]))

In [4]:

n = len(data)

print(f"Количество элементов в выборке =", n)

Количество элементов в выборке = 320

[↑] 1. Статистики выборки $x_1, \ldots, x_n$ :¶

[↑] A. Среднее:¶

Среднее значение — числовая характеристика множества чисел или функций (в математике); — некоторое число, заключённое между наименьшим и наибольшим из их значений. Среднее, как абстрактная характеристика совокупности, отражает типичный уровень (размер) признака, типичные черты и cвойства всех единиц изучаемой совокупности, поэтому среднее отвлекается (абстрагируется) от индивидуальных особенностей отдельных единиц.

О разновидностях среднего можно прочитать по ссылке.

[↑] a. Арифметическое¶

В исходной задаче для получения среднего значения корректно использовать среднее арифметическое, вычисляемое по формуле:

$\overline{x} = \frac{x_1 + x_2 + \ldots + x_n}{n} = \frac{1}{n}\sum\limits_{i=1}^n x_i$

In [5]:

mean = data.mean()

print(f"Среднее арифметическое = {mean:.2f}")

Среднее арифметическое = 100.86

[↑] b. Гармоническое¶

Используется при расчетах скорости, производительности, цены и рассчитывается по формуле:

$H(x_1, ..., x_n) = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \ldots + \frac{1}{x_n}} = \frac{n}{\frac{1}{n}\sum\limits_{i=1}^n \frac{1}{x_i}}$

In [6]:

def harmonic_mean(data: np.ndarray) -> float:
    return np.size(data) / np.sum(1.0 / data)

print(f"Среднее гармоническое = {harmonic_mean(data):.2f}")

Среднее гармоническое = 88.37

[↑] c. Геометрическое¶

Используется в расчетах инвестиций, прироста, площади, объёма и рассчитывается по формуле:

$\overline{x}_{геом} = \sqrt[n]{\prod\limits_{i=1}^n x_i} = \sqrt[n]{x_1 \cdot x_2 \cdot \ldots \cdot x_n}$

In [7]:

def geometric_mean(data: np.ndarray) -> float:
    return np.exp(np.log(data).mean())

print(f"Среднее геометрическое = {geometric_mean(data):.2f}")

Среднее геометрическое = 95.48

[↑] B. Медиана¶

В основе среднего значения лежит закон больших чисел и допущение, что исходая величина распределена нормально. Это подразумевает, что возможные значения сконцентрированы вокруг некоторого наиболее частого значения, а отклонения и в большую, и в меньшую сторону относительно невелики и равновероятны.

В случае отклонения распределения от нормального среднее значение использовать некорректно, так как оно является слишком чувствительным параметром к «выбросам» – нехарактерным для изучаемой выборки, слишком большим или слишком малым значением, поэтому в таких случаях используется медиана.

Медиана – это значение признака, справа и слева от которого находится равное число наблюдений (по 50%). Этот параметр в отличие от среднего значения устойчив к «выбросам». Заметим также, что медиана может использоваться и в случае нормального распределения – в этом случае медиана совпадает со средним значением.

Пусть выборка отсортирована, и размер выборки равен $n$ , тогда:

• Если $n$ - нечетное, то медиана $Мe = x_{Me} = x_{p+1}$ , где $p = \frac{n-1}{2}$

• Если $n$ - четное, то медиана $Мe = x_{Me} = \frac{x_p + x_{p+1}}{2}$ , где $p = \frac{n}{2}$

In [8]:

def median(data: np.ndarray) -> float:
    return np.median(data)

print(f"Медиана выборки = {median(data)}")

Медиана выборки = 101.0

[↑] C. Мода¶

Мода — значение во множестве наблюдений, которое встречается наиболее часто. (Мода = типичность.)

Иногда в совокупности встречается более чем одна мода (например: $6, 2, 6, 6, 8, 9, 9, 9, 0$ ; мода — $6$ и $9$ ). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило, мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.

Мода как средняя величина употребляется чаще для данных, имеющих нечисловую природу. Среди перечисленных цветов автомобилей — белый, чёрный, синий металлик, белый, синий металлик, белый — мода будет равна белому цвету. При экспертной оценке с её помощью определяют наиболее популярные типы продукта, что учитывается при прогнозе продаж или планировании их производства.

Определяется по формуле:

$Mo = x_i | m_i = \max\limits_{j=\overline{1, n}}\{m_j\}$

Функция, вычисляющая моду выборки:

In [9]:

def mode(data: np.ndarray) -> np.ndarray:
    vals, counts = np.unique(data, return_counts=True)
    return vals[np.where(counts == np.max(counts))]

print(f"Мода выборки = {mode(data)}")

Мода выборки = [69 74]

Проверим функцию на корректность. Для этого подсчитаем количество значений в выборке:

In [10]:

Counter(data).most_common(5)

Out[10]:

[(69, 9), (74, 9), (100, 8), (92, 7), (103, 7)]

[↑] D. Нижний и верхний $0,05$ -квантиль, квартили $Q_1, Q_2, Q_3$ , интерквартильный размах¶

$\alpha$ -квантиль (квантиль порядка $\alpha$ ) — это значение уровня, ниже которого лежит определенное число наблюдений, соответствующих выбранной частоте $\alpha$ . Таким образом, $\alpha$ -квантиль — это статистика, равная элементу вариационного ряда с номером $[n\alpha+1]$ , где квадратные скобки означают целую часть.

Выделяют следующие квантили:

Нижний $\alpha$ -квантиль - это о же, что и обычный квантиль порядка $\alpha$ ;
Верхний $\alpha$ -квантиль - это обычный квантиль порядка $1-\alpha$ .

Квартили — это квантили, кратные 25%.

Выделяют следующие квартили:

$Q_1$ — это $\frac{1}{4}(n+1)$ — ранжированное наблюдение — первый (нижний) квартиль — значение вариационного ряда данных, левее которого находится четверть (25%) всех наблюдений;
$Q_2$ — это $\frac{1}{2}(n+1) = Me$ — это медиана $Me$ , левее и правее которой находится половина всех значений;
$Q_3$ — это $\frac{3}{4}(n+1)$ — ранжированное наблюдение — третий (верхний) квартиль — значение вариационного ряда данных, правее которого находится четверть всех наблюдений.

Интерквартильный размах — отражает среднюю половину (50%) данных. Вычисляется по формуле:

$IQR = Q_3 - Q_1$

Пример:

Для выборки имеем следующие статистики:

In [11]:

def quantile(data: np.ndarray, quantile: float) -> float:
    return int(np.quantile(data, quantile))

Q1 = quantile(data, 0.25)
Q3 = quantile(data, 0.75)

IQR = Q3 - Q1

print(f"Нижний 0.05-квантиль = {quantile(data, 0.05)}",
      f"Верхний 0.05-квантиль = {quantile(data, 1 - 0.05)}",
      f"Q1 = {Q1}",
      f"Q2 = {quantile(data, 0.5)}",
      f"Q3 = {Q3}",
      f"Интерквартильный размах = {IQR}", sep="\n")

Нижний 0.05-квантиль = 54
Верхний 0.05-квантиль = 152
Q1 = 78
Q2 = 101
Q3 = 121
Интерквартильный размах = 43

[↑] E. Выборочная дисперсия:¶

Дисперсия случайной величины — мера разброса значений случайной величины относительно её математического ожидания.

Выборочная дисперсия — это оценка теоретической дисперсии распределения, рассчитанная на основе данных выборки.

Дисперсия имеет размерность, равную квадрату размерности признака. Это значит, к примеру, что если признак $x$ измеряется в рублях, то размерность дисперсии - $[руб^2]$ , что является её недостатком.

[↑] a. Несправленная (смещенная)¶

Под выборочной дисперсией часто понимают неисправленную (смещенную) выборочную дисперсию. Её формула равна:

$S^2 = \frac{1}{n}\sum\limits_{i=1}^n \left(x_i-\overline{x}\right)^2$

Однако чаще используется формула:

$S^2 = \frac{1}{n}\sum\limits_{i=1}^n x_i^2 - \left(\sum\limits_{i=1}^n x_i \right)^2 = \overline{x^2} - \overline{x}^2$

In [12]:

var = np.var(data) # var == variance

print(f"Выборочная неисправленная дисперсия = {var:.2f}")

Выборочная неисправленная дисперсия = 944.74

[↑] b. Исправленная (несмещенная)¶

Если в качестве оценки генеральной дисперсии принять выборочную дисперсию $D_в$ , то эта оценка будет приводить в систематическим ошибкам, давая заниженное значение генеральной дисперсии $D_г$ . Объясняется это тем, что, как можно доказать, выборочная дисперсия является смещенной оценкой, другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно:

$M[D_в] = \frac{n}{n-1}D_г$

Легко исправить выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить $D_в$ на дробь $\frac{n}{n-1}$ . Получим формулу исправленной выборочной дисперсии:

$\hat{S}^2 = \frac{n}{n-1}S^2 = \frac{1}{n-1}\sum\limits_{i=1}^n \left(x_i-\overline{x}\right)^2$

Исправленная дисперсия является несмещенной оценкой генеральной дисперсии. Действительно:

$M\left[\hat{S}^2\right] = M\left[\frac{n}{n-1}D_г\right] = \frac{n}{n-1} M[D_в] = \frac{n}{n-1}\cdot \frac{n-1}{n} D_г = D_г$

In [13]:

unbiased_var = np.var(data, ddof=1)

print(f"Выборочная исправленная дисперсия = {unbiased_var:.2f}")

Выборочная исправленная дисперсия = 947.71

[↑] F. Стандартное отклонение¶

Чтобы избавиться от квадрата размерности признака в дисперсии, была введена такая статистическая характеристика, как стандартное (среднее квадратическое) отклонение. Формула имеет вид:

$S = \sqrt{S^2}$ где

$S^2$ — выборочная дисперсия;

Стандартное отклонение, подобно дисперсии, также может быть смещенным и несмещенным. Вычислим смещенное стандартное отклонение:

In [14]:

std = np.std(data) # == np.sqrt(var)

print(f"Смещенное стандартное отклонение = {std:.2f}")

Смещенное стандартное отклонение = 30.74

А также несмещенное стандартное отклонение:

In [15]:

unbiased_std = np.std(data, ddof=1)

print(f"Несмещенное стандартное отклонение = {unbiased_std:.2f}")

Несмещенное стандартное отклонение = 30.78

[↑] G. Стандартная ошибка среднего¶

Стандартная ошибка — величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Цель этой метрики — помочь определить границы в которых может варьироваться истинное среднее для всей генеральной совокупности на основе некоторой выборки.

Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Стандартная ошибка среднего рассчитывается по формуле:

$SEM = \frac{S}{\sqrt{n}}$ где

$S$ — стандартное отклонение;

In [16]:

def sem(data):
    return np.std(data) / np.sqrt(np.size(data))

print(f"Стандартная ошибка среднего = {sem(data):.2f}")

Стандартная ошибка среднего = 1.72

[↑] H. Коэффициент вариации¶

Коэффициент вариации (относительное стандартное отклонение) — мера относительного разброса случайной величины. Показывает, какую долю среднего значения этой величины составляет её средний разброс. Он применяется для сравнения вариативности одного и того же признака в нескольких совокупностях с различным средним арифметическим.

Формула коэффициента вариации:

$V_S = \frac{S}{\overline{x}}$ где

$S$ — стандартное отклонение;

Однако чаще используется представление в процентах:

$V_S = \frac{S}{\overline{x}}\cdot100\%$

In [17]:

def variation(data: np.ndarray, in_percents=False) -> float:
    cv = np.std(data) / np.mean(data)
    return cv * 100 if in_percents else cv

print(f"Коэффициент вариации = {variation(data, True):.2f}%")

Коэффициент вариации = 30.47%

[↑] I. Моменты распределения¶

Момент $k$ -го порядка — среднее арифметическое $k$ -й степени отклонения наблюдаемых значений $x_i = (i = 1, 2, \ldots, n)$ от некоторой постоянной $c$ , то есть:

$\mu_k^{(c)} = \sum\limits_{i=1}^n (x_i-c)^k$ При

$c=0$ имеем начальный момент $k$ -го порядка:

$v_k=\frac{1}{n}\sum\limits_{i=1}^n x_i^k$ При

$c=\overline{x}$ имеем центральные моменты $k$ -го порядка:

$\mu_k^{(c)} = \sum\limits_{i=1}^n \left(x_i-\overline{x}\right)^k$

Если $c=\overline{x}$ и $k=0$ , то $\mu_0=1$ ;
Если $c=\overline{x}$ и $k=1$ , то $\mu_1=0$ ;
Если $c=\overline{x}$ и $k=2$ , то $\mu_2$ есть дисперсия: $\mu_2 = \frac{1}{n}\sum\limits_{i=1}^n \left(x_i-\overline{x}\right)^2$

Центральные моменты третьего и четвертого порядков обычно используются не сами по себе, а для расчета коэффициентов асимметрии и эксцесса.

[↑] J. Коэффициент ассиметрии¶

Коэффициет ассиметрии — величина, характеризующая асимметрию (скошенности) распределения случайной величины.

Определяется по формуле:

$Ac = \frac{\mu_3}{S_3}$ где

$\mu_3 = \frac{1}{n}\sum\limits_{i=1}^n \left(x_i - \overline{x}\right)^3$ — центральный момент третьего порядка,

$S$ — стандартное отклонение;

Если $Ac>0$ , то распределение имеет правостороннюю ассиметрию (более пологий спуск справа);
Если $Ac<0$ , то распределение имеет левостороннюю ассиметрию;
Если $Ac=0$ , то это идеально симметричное распределение.

Если $|Ac|>0.5$ , то ассиметрия существенна.

In [18]:

skewness = stats.skew(data, bias=False)

print(f"Коэффициент ассиметрии = {skewness:.2f}")

Коэффициент ассиметрии = 0.10

[↑] K. Коэффициент эксцесса¶

Коэффициент эксцесса — мера остроты пика распределения случайной величины.

Определяется по формуле:

$Ek = \frac{\mu_4}{S_4}-3$ где

$\mu_4 = \frac{1}{n}\sum\limits_{i=1}^n \left(x_i - \overline{x}\right)^4$ — центральный момент четвертого порядка,

$S$ — стандартное отклонение;

Если $Ek>0$ , то пик распределения случайной величины остроконечен;
Если $Ek<0$ , то пик распределения случайной величины плосковершинный:

In [19]:

kurtosis = stats.kurtosis(data, bias=False)

print(f"Коэффициент эксцесса = {kurtosis:.4f}")

Коэффициент эксцесса = 0.0227

[↑] 2. Диаграмма Box-whiskers, определение выбросов¶

Ящик с усами, диаграмма размаха (англ. box-and-whiskers diagram or plot, box plot) — график, использующийся в описательной статистике, компактно изображающий одномерное распределение вероятностей.

Такой вид диаграммы в удобной форме показывает медиану (или, если нужно, среднее), нижний и верхний квартили, минимальное и максимальное значение выборки и выбросы. Несколько таких ящиков можно нарисовать бок о бок, чтобы визуально сравнивать одно распределение с другим; их можно располагать как горизонтально, так и вертикально. Расстояния между различными частями ящика позволяют определить степень разброса (дисперсии) и асимметрии данных и выявить выбросы.

Сравнение плотности распределения и ящика с усами:

Сопоставление нормального распределения и ящика с усами:

Построим ящик с усами для исходной выборки:

In [20]:

box_plt = plt.boxplot(data, vert=False)

plt.show()

Выброс (англ. outlier) — резко отклоняющееся значение наблюдаемой величины. Выбросом считается наблюдение, которое лежит аномально далеко от остальных из серии параллельных наблюдений.

Поскольку множество статистических методов «буксуют» на выборках с выбросами, выбросы приходится обнаруживать (желательно — автоматически) и исключать из выборки. Простейшие способы основаны на межквартильном расстоянии — например, считать выбросами всё, что не попадает в диапазон:

$[Q1-1.5\cdot IQR, Q3+1.5\cdot IQR]$

Более тонкие критерии — критерий Шовене, критерий Граббса, критерий Пирса, критерий Диксона.

Получим выбросы исходной выборки, используя межквартильное расстояние:

In [21]:

print("Выбросы исходной выборки =",
      data[(data < Q1 - 1.5 * IQR) | (data > Q3 + 1.5 * IQR)])

Выбросы исходной выборки = [ 11 186 186 200]

Также можно получить выбросы, используя объект boxplot:

In [22]:

outliers = box_plt["fliers"][0].get_data()[0]

print("Выбросы исходной выборки =",
      outliers)

Выбросы исходной выборки = [ 11 186 186 200]

In [23]:

del box_plt, outliers

[↑] 3. Интервальный ряд c использованием формулы Стёрджеса¶

Сгруппированным интервальным (непрерывным) вариационным рядом называют ранжированные по значению признака интервалы $(a_i \leq x < b_i)$ , где $i=1, 2, \cdots, k$ , указанные вместе с соответствующими частотами $m_i$ числа наблюдений, попавших в $i$ -й интервал или относительными частотами $\frac{m_i}{n}$ .

Построение интервального вариационного ряда начинают с определения числа $k$ , обозначающее количество интервалов. Оно должно быть оптимальным. Если оно будет малым, то гистограмма получется слишком сглаженной (oversmoothed) и потеряет все особенности изменчивости данных. Если будет большим, то мы не сможем оценить плотность распределения изучаемых данных по числовой оси: гистограмма получится недосглаженная (undersmoothed), с незаполненными интервалами, неравномерная.

Чаще всего для определения числа $k$ используется формула Стёрджеса:

$k=1+ \lfloor \log_2n \rfloor = 1 + \lfloor 3,22 \lg n \rfloor$

где $\lfloor \dots \rfloor$ — округление вниз до целого;

Алгоритм построения интервального ряда получается следующим:

Определение $x_{max}$ и $x_{min}$ в имеющейся выборке;
Определение размаха варьирования признака $R = x_{max} - x_{min}$ ;
Определение количества бинов $k$ формулой Стёрджеса;
Определение ширины интервала $h = \frac{R}{k}$ ;
Определение граничных значений интервалов $(a_i, b_i)$ . Рекомендуется отступить влево от нижнего предела варьирования $a_1 = x_{min} - \frac{h}{2}$ . Верхняя граница первого интервала $b_1 = a_1 + h$ . Далее используют итеративную формулу: $a_{i+1} = b_i$ ; $b_i = a_i + h$ . Построение интервалов продолжается до тех пор, пока начало следующего по порядку интервала не будет равным или больше $x_{max}$ ;
Группировка результатов наблюдения: при просмотре статистических данных значения признака разносятся по соответствующим интервалам.

In [24]:

# Правило Стёрджеса -> оптимальное число бинов в гистограмме
def sturges(arr: np.ndarray) -> int:
    return int(1 + np.floor(np.log2(len(arr))))

occur, intervals = np.histogram(data, bins=sturges(data))

print(f"Оптимальное количество интервалов = {sturges(data)}",
      f"Получившийся интервальный ряд = {intervals}", sep="\n")

Оптимальное количество интервалов = 9
Получившийся интервальный ряд = [ 11.  32.  53.  74.  95. 116. 137. 158. 179. 200.]

[↑] 4. График эмпирической функции распределения $F_n$ ¶

Эмпирическая функция распределения (функция распределения выборки) — функция, которая определяет для каждого значения $x$ частоту событий $X<x$ и предназначена для оценки теоретической функции распределения генеральной совокупности в математической статистике.

Эмпирическая функция распределения находится по формуле:

$F_n = \frac{n_x}{n}$ где

$n_x$ — количество вариантов, меньших

$x$ ,

$n$ — объём выборки.

Функция распределения $F_x$ генеральной совокупности называется теоретической функцией распределения. Отличие эмпирической функции от теоретической состоит в том, что теоретическая функция определяет вероятность события $X<x$ , а эмпирическая стремится к ней при большом количестве испытаний.

Несколько примеров плотностей вероятности и функций распределения:

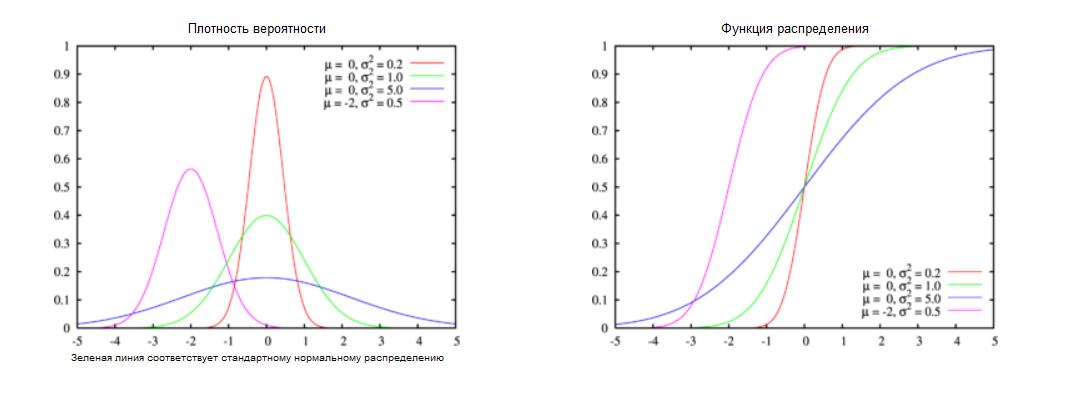
Вычислим эмпирическую функцию распределения для исходной выборки:

In [25]:

# Эмпирическая функция распределения
def ecdf(X: np.ndarray, size: int = None) -> np.ndarray:
    return np.arange(1, len(X) + 1) / len(X) if size is None else np.arange(1, len(X) + 1) / size

plt.step(data, ecdf(data))

plt.ylabel('$F_n$', fontsize=20)
plt.xlabel('$x$', fontsize=20)

plt.show()

[↑] 5. Проверка распределения на нормальность:¶

[↑] A. Гистограмма¶

Проверим распределение на нормальность с использованием гистограммы:

In [26]:

# Гистограмма
plt.hist(data, bins=sturges(data), density=True)

# Нормальное распределение
x_pdf = np.linspace(np.min(data), np.max(data), 1000)
y_pdf = stats.norm.pdf(x_pdf, loc=mean, scale=std)

plt.plot(x_pdf, y_pdf, lw=4, c='r')
plt.show()

Заметим, что данные исходной выборки распределены нормально

[↑] B. QQ-plot¶

QQ-plot (график квантиль-квантиль) — графический метод определения принадлежности выборки определенному распределению, дополнительно позволяющий:

Оценивать степень отклонения данных от теоретического распределения;
Читать медиану, дисперсию и наклон функции распределения;
Сравнивать две выборки между собой.

In [27]:

stats.probplot(data, dist="norm", plot=plt)
plt.show()

[↑] С. Критерий ассиметрии и эксцесса¶

Критерий ассиметрии и эксцесса мы уже рассчитывали выше. Они получились достаточно близки к нулю:

In [28]:

print(f"Коэффициент ассиметрии = {skewness:.2f}",
      f"Коэффициент эксцесса = {kurtosis:.2f}", sep="\n")

Коэффициент ассиметрии = 0.10
Коэффициент эксцесса = 0.02

Так как критерии ассиметрии и эксцесса могут иметь место и для распределений, отличных от нормального, то этот критерий следует воспринимать как критерий установления отклонения от нормальности распределения, но не установления нормальности.

In [29]:

del skewness, kurtosis

[↑] D. Проверка гипотез¶

Критерием согласия называется метод проверки гипотезы о предполагаемом законе неизвестного распределения.

Критерий согласия — алгоритм, предназначенный для проверки гипотезы $H_0$ о том, что ряд наблюдений $x_1, x_2, \cdots x_n$ образует случайную выборку, извлеченную из генеральной совокупности $X$ с функцией распределение $F(x)=F(x,\theta)$ :

$H_0: F_n(x)=F(x,\theta)$

где $F_n(x)$ эмпирическая функция распределения, $\theta=(\theta_1, \theta_2, \cdots, \theta_k)$ — вектор параметров. Общий вид функции $F(x, \theta)$ считается известным, а параметры $\theta_1, \theta_2, \cdots, \theta_k$ могут быть как известными, так и неизвестными.

Большинство критериев согласия основаны на использовании различных мер расстояний между анализируемой эмпирическое функцией $F_n(x)$ распределения, определенной по выборке, и функцией распределения $F(x, \theta)$ генеральной совокупности $X$

$\alpha$ -уровень (уровень значимости) — пороговый уровень статистической значимости; вероятность ошибочно отклонить нулевую гипотезу. Чем меньше $\alpha$ -уровень, тем меньше риск совершения этой ошибки. Устанавливается исследователем произвольно (обычно принимается равным $0.05$ , $0.01$ или $0.001$ ). Примем уровень значимости равным $0.05$ :

In [30]:

confidence = 0.05

[↑] E. Критерий согласия хи-квадрат Пирсона¶

Данный критерий служит для проверки гипотезы о том, что генеральная совокупность, из которой извлечена выборка, имеет заданный закон распределения. Применяется при объемах выборки $n \geq 50$ .

Пусть имеется выборка $\{x_i\}_{i=1}^n$ объема $n$ . Необходимо проверить гипотезу о том, что выборка была извлечена из генеральной совокупности, распределенной по закону с функцией распределения $F(x, \theta)$ :

$H_0 : F_n(x) = F(x, \theta)$

где $\theta$ — известный вектор параметров теоретического закона

По выборке $\{x_i\}_{i=1}^n$ получим эмпирическое распределение в виде дискретного или интервального вариационного ряда:

где $m_i$ - количество наблюдений в $i$ -м интервале.

Обозначим через $p_i$ вероятности попадания $i$ -й интервал $\left(i=\overline{1, k}\right)$ , соответствующие теоретическому закону с функцией распределения $F(x, \theta)$ :

$p_i = P\left(a_{i} < x < b_{i}\right) = F\left(b_{i}, \theta\right) - F\left(a_{i}, \theta\right)$

Вероятности $p_i$ можно рассматривать как теоретические частости:

$p_i=\frac{m'_i}{n}$ где

$m'_i=np_i$

Величины $m'_i$ можно рассматривать как теоретические частоты, т.е. количества элементов выборки, которые должны были попасть в каждый интервал, если бы случайная величина имела выбранный закон распределения $F(x, \theta)$ , параметры которого совпадают с их то тчечными оценками по выборке.

Каждая из величин

$\frac{m_i - m'_i}{\sqrt{m'_i}}$

представляет собой относительное отклонение частоты от теоретической частоты и имеет стандартное нормальное распределение. Соответственно, сумма квадратов этих величин имеет распределение хи-квадрат.

Справедлива следующая теорема.

Теорема. Величина

$\chi^2_n = \sum\limits_{i=1}^k \frac{(m_i-np_i)^2}{np_i} = \sum\limits_{i=1}^k \frac{\left(m_i-m'_i\right)^2}{m'_i}$

является случайной и, если верна проверяемая гипотеза $H_0 : F_n(x)= F(x, \theta)$ , распределена по закону $\chi^2$ с числом степеней свободы $v=k-1-r,$ где $k$ — число частичных интервалов выборки, $r$ — число параметров преполагаемого распределения.

Далее вычисляем теоретическое (истинное) $\chi^2_{v;\alpha}$ для заданной вероятности $\alpha$ :

$\chi^2_{v;\alpha} | P\left(\chi^2 > \chi^2_{v;\alpha}\right) = \alpha$

То есть $\chi^2_{v;\alpha}$ — $\alpha$ -квантиль распределения хи-квадрат. Его также называют критическим значением и находят по таблицам распределения $\chi^2$ .

Гипотеза $H_0$ отвергается на уровне значимости $\alpha$ , если вычисленное значение $\chi^2_n$ окажется больше критического $\chi^2_{v;\alpha}$ :

$\chi^2_n > \chi^2_{v;\alpha}$

Геометрически это означает, что $\chi^2_n$ попадает в правостороннюю критическую область, граница которой при заданном уровне значимости $\alpha$ равна $\chi^2_{v;\alpha}$

Иногда оценивается вероятность получить значение статистики $\chi^2_n$ :

$p\_value = P\left(\chi^2 > \chi^2_n \right)$

Если $p\_value < \alpha$ , то гипотеза $H_0$ отвергается.

Для проверки гипотезы о нормальном законе распределения находим вероятности по формуле:

$p_i = p\left(x_i < x < x_{i+1}\right) = \Phi\left(\frac{x_{i+1} - \overline{x}}{S}\right) - \Phi\left(\frac{x_i - \overline{x}}{S}\right)$ где

$n$ — объем выборки;

$x_i, x_{i+1}$ — левая и правая границы

$i$ -го интервала;

$\Phi$ — функция стандартного нормального распределения;

$\overline{x}$ — выборочное среднее;

$S$ — исправленное стандартное отклонение. Далее находим теоретические частоты

$m'_i = np_i$

Поскольку нормальное распределение характеризуется 2 параметрами $\mu$ и $\sigma$ , то $r=2$ и число степеней свободы $v=n-3$ .

Вычислим теоретические частоты $m'_i$ для исходной выборки:

In [31]:

cdf = stats.norm.cdf

m_t = [(cdf(intervals[i+1], mean, std) - cdf(intervals[i], mean, std)) * n
        for i in range(len(intervals) - 1)]

print(f"Теоретические частоты = {m_t}")

Теоретические частоты = [3.4568097474664263, 15.098115892487069, 42.03427772166201, 74.65478800282929, 84.62272793942867, 61.226142268367205, 28.267755294164374, 8.32308541501277, 1.5614375004549785]

Затем вычислим значение $\chi^2_n$ по формуле:

In [32]:

chi_sq = np.sum((occur - m_t) ** 2 / m_t)

print(f"Хи-квадрат = {chi_sq:.3f}")

Хи-квадрат = 4.011

Получим критическое значение $\chi^2_{v;\alpha}$ , используя функцию chi2.ppf из модуля scipy.stats:

In [33]:

crit_val = stats.chi2.ppf(1 - confidence, sturges(data) - 3)

print(f"Критическое значение = {crit_val:.3f}")

Критическое значение = 12.592

Таким образом, неравенство $\chi^2_n > \chi^2_{v;\alpha}$ не выполняется. Следовательно, гипотеза $H_0$ о нормальности распределения не отвергается.

[↑] F. Критерий Колмогорова¶

Если невозможно эффективно применять хи-квадрат на маленьких выборках, то в таких случаях часто используется критерий Колмогорова. Данный критерий также предназначен для проверки простых гипотез о принадлежности анализируемой выборки некоторому полностью известному параметрическому закону распределения.

Применяется критерий Колмогора по следующей схеме:

Строится эмпирическая функция $F_n(x)$ :
Определяется мера расхождения между теоретическим и эмпирическим распределением по формуле $D_n = \max\limits_i |F_n(x_i) - F(x_i)|$ и вычисляется величина:
$k_n = \sqrt{n}{D_n}$
Находится критическое значение $k_\alpha$ . Значение можно найти в соответствующих таблицах или приблизительно рассчитать по формуле:

$k_\alpha \approx \sqrt{\frac{1}{2} \ln \frac{2}{\alpha}}$

Если $k_n > k_\alpha$ , то нулевая гипотеза $H_0$ о том, что случайная величина $X$ имеет заданный закон распределения, отвергается. Иначе гипотеза не противоречит опытным данным.

Реализуем функции, необходимые для проверки нулевой гипотезы о принадлежности выборки нормальному распределнию критерием Колмогорова:

In [34]:

# Теоретическая функция нормального распределения
def tcdf(X: np.ndarray) -> np.ndarray:
    return np.array([cdf(x, loc=X.mean(), scale=X.std()) for x in X])

# Мера расхождения между теоретической и эмпирической функцией
def Dn(Ft: np.ndarray, Fx: np.ndarray) -> float:
    return np.max(np.abs(Ft - Fx))

# Статистика критерия Колмогорова
def kn(Dn: float, n: int) -> float:
    return np.sqrt(n) * Dn

# Критическое значение для статистики критерия Колмогорова
def k_conf(confidence: float) -> float:
    return np.sqrt(0.5 * np.log(2 / confidence))

# Конвертация в стандартное нормальное распределение
def to_std_norm_dist(X: np.ndarray) -> np.ndarray:
    return (X - X.mean()) / X.std()

В соответствии со схемой последовательно воспользуемся ими. Вычислим $D_n$ :

In [35]:

print(f"Мера расхождения Dn = {Dn(tcdf(data), ecdf(data)):.3f}")

Мера расхождения Dn = 0.031

Вычислим статистику критерия Колмогорова $k_n$ и критическое значение $k_\alpha$ :

In [36]:

print(f"Статистика Колмогорова kn = {kn(Dn(tcdf(data), ecdf(data)), n):.3f}")
print(f"Критическое значение k_confidence = {k_conf(0.05):.3f}")

Статистика Колмогорова kn = 0.561
Критическое значение k_confidence = 1.358

Таким образом, неравенство $k_n > k_\alpha$ не выполняется. Следовательно, гипотеза нормальности нормальности распределения не отвергается.

Проверим правильность вычислений с помощью функции kstest из scipy.stats:

In [37]:

print("Мера расхождения Dn = {:.3f} \np_value = {:.3f}".format(*stats.kstest(to_std_norm_dist(data), 'norm')))

Мера расхождения Dn = 0.031 
p_value = 0.902

Меры расхождения $Dn$ равны и $p\_value > \alpha = 0.05$ . Таким образом, гипотеза о нормальности распределения также не отвергается.

[↑] 6. Проверка первых 10 значений на нормальность, используя критерий Шапиро-Уилка¶

Критерий Шапиро-Уилка предназначен для проверки на нормальность распределения выборок, численностью от 3 до 50. В отличии от критериев Пирсона и Колмогорова, критерий Шапиро–Уилка может быть использовал лишь для проверки распределения на нормальность.

Пусть имеется выборка $(x_1, x_2, \cdots, x_n)$ , где $3 \leq n \leq 50$ . Вычисления производятся по формуле:

$W=\frac{b^2}{S^2}$

где $S^2 = \sum\limits_{i=1}^n \left(x_i-\overline{x}\right)^2$ — квадрат оценки среднеквадратического отклонения Ллойда; $b = \sum\limits_{i=1}^k a_{n-i+1}(x_{n-i+1}-x_i)$ ; $k=\frac{n}{2}$ , eсли $n$ - четное, иначе $k=\frac{n-1}{2}$ ; $a_{n-i+1}(i=1, \cdots, k)$ — известные константы, которые вычисляются, либо берутся из заданных таблиц:

Если $W<W(\alpha)$ , то нулевая гипотеза нормальности распределения отклоняется на уровне значимости $\alpha$ . Значения $W(\alpha)$ также приводятся в таблицах:

Полные таблицы приведены в книге Кобзарь А.И. — Прикладная математическая статистика. Для инженеров и научных работников.

Вычислим $W$ для первых десяти значений в отсортированной исходной выборке:

In [38]:

N = 10
a = np.array([0.5739, 0.3291, 0.2141, 0.1224, 0.0399])

b = np.sum([a[i] * (data[N-i-1] - data[i]) for i in range(N // 2)])
W = b**2 / (N * np.var(data[:N]))

print(f"W = {W:.3f}")

W = 0.879

Если принять уровень значимости $\alpha$ равным $0.05$ , то, используя прикрепленную выше таблицу, можно найти значение $W(\alpha)$ . Видим, что при $n=10$ и $\alpha=0.05$ :

$W(\alpha)=0.842$

Таким образом, неравенство $W < W(\alpha)$ не выполняется. Следовательно, гипотеза нормальности распределения принимается.

Посчитаем также критерий Шапиро-Уилка с использованием функции shapiro из scipy.stats:

In [39]:

stats.shapiro(data[:10])

Out[39]:

ShapiroResult(statistic=0.8784602880477905, pvalue=0.12528105080127716)

Заметим, что функция возвращает ещё один параметр $p\_value$ . Если $p\_value < \alpha$ , то гипотеза отвергается.

В нашем случае $0.125 \nless 0.05$ , что также подтвержает гипотезу нормальности распределения.

In [40]:

del a, b, N

[↑] 7. $95\%$ -й доверительный интервал для неизвестной генеральной дисперсии¶

Доверительный интервал для неизвестной генеральной дисперсии имеет следующий вид:

$\left(\frac{(n-1) \cdot S^2}{\chi_l^2(\alpha)}; \frac{(n-1) \cdot S^2}{\chi_r^2(\alpha)}\right)$

где $S^2$ — исправленная выборочная дисперсия, $\chi^2$ — распределения с $n-1$ степенью свободы, причем в таблице ищем $\frac{\alpha}{2}$ и $1 - \frac{\alpha}{2}$ соответственно.

In [41]:

chi_l = stats.chi2.ppf(confidence / 2, n - 1)
chi_r = stats.chi2.ppf(1 - confidence / 2, n - 1)

D_conf_interval = ((n - 1) * unbiased_var / chi_r, (n - 1) * unbiased_var / chi_l)

print("Доверительный интервал для дисперсии:",
      "({:.2f}, {:.2f})".format(*D_conf_interval))

Доверительный интервал для дисперсии: (816.25, 1113.86)

[↑] 8. $95\%$ -й доверительный интервал для неизвестного генерального среднего при условии, что:¶

[↑] A. Генеральные дисперсии известны¶

Использовать данные, полученные в пункте 7

Доверительный интервал для среднего с известной дисперсией имеет вид:

$\left(\overline{x} - \frac{\sigma}{\sqrt{n}} \cdot z_\alpha;\; \overline{x} + \frac{\sigma}{\sqrt{n}} \cdot z_\alpha\right)$

где $\sigma$ — выборочное несмещенное стандартное отклонение, $z_\alpha$ — квантиль нормального распределения уровеня $1 - \frac{\alpha}{2}$

или

$\left(\overline{x} - \Delta;\; \overline{x} + \Delta\right)$

где $\Delta = \frac{\sigma}{\sqrt{n}} \cdot z_\alpha$ ;

Чтобы вычислить выборочное несмещенное стандартное отклонение, извлечем корень из уже вычисленной исправленной (несмещенной) дисперсии:

In [42]:

unbiased_std = np.sqrt(unbiased_var)

Вычислим $\Delta$ и получим доверительные интервалы для неизвестного генерального среднего:

In [43]:

delta = stats.distributions.norm.ppf(1 - confidence / 2) * unbiased_std / np.sqrt(n)
E_conf_interval = mean - delta, mean + delta

print("Доверительный интервал для неизвестного генерального среднего:",
      "({:.2f}, {:.2f})".format(*E_conf_interval))

Доверительный интервал для неизвестного генерального среднего: (97.49, 104.24)

Проверим полученные результаты с использованием встроенных функций:

In [44]:

def confidence_interval(data: np.ndarray, conf: float = 0.95) -> tuple[float, float]:
    return stats.t.interval(conf, len(data)-1, data.mean(), stats.sem(data))

print("Доверительный интервал для неизвестного генерального среднего:",
      "({:.2f}, {:.2f})".format(*confidence_interval(data)))

Доверительный интервал для неизвестного генерального среднего: (97.48, 104.25)

[↑] B. Генеральные дисперсии неизвестны¶

Если выборка больше 30, но стандартное отклонение нам неизвестно, то вместо $\sigma$ мы будем использовать выборочное стандартное отклонение:

$s = \sqrt{\frac{1}{n-1}\sum_\limits{i=1}^n \left( x_i - \overline{x} \right)^2}$

Таким образом, доверительный интервал для среднего при неизвестной дисперсии, но большой выборке ( $n > 30$ ), имеет вид:

$\left(\overline{x}-\frac{s}{\sqrt{n}}z_\alpha;\; \overline{x}+\frac{s}{\sqrt{n}}z_\alpha\right)$

In [45]:

s = np.sqrt(np.sum((data - mean) ** 2) / (n - 1))
delta = stats.norm.ppf(1 - confidence / 2) * s / (n ** 0.5)
E_conf_interval = (mean - delta, mean + delta)

print("Доверительный интервал для неизвестного генерального среднего:",
      "({:.2f}, {:.2f})".format(*E_conf_interval))

Доверительный интервал для неизвестного генерального среднего: (97.49, 104.24)

[↑] 9. Разбиение выборки на 2 непересекающиеся группы в пропорции $55/45$ в произвольном порядке и проверка групп:¶

Разбиваем выборку по условию:

In [46]:

sample_1, sample_2 = train_test_split(data, train_size=0.55, random_state=0)

n1, n2 = len(sample_1), len(sample_2)

print(f"Размерность выборок = {(n1, n2)}")

Размерность выборок = (176, 144)

[↑] A. На однородность с использованием критерия Колмогорова-Смирнова¶

Критерий Колмогорова-Смирнова используется для проверки гипотезы об однородности выборок, то есть гипотезу о том, что рассматриваемые выборки извлечены из одной и той же генеральной совокупности:

$H_0 : F_1(x) = F_2(x)$

Статистика критерия Колмогорова-Смирнова имеет вид:

$k_{n, m} = \sqrt{\frac{nm}{n+m}} \cdot D_{n, m} = \sqrt{\frac{nm}{n+m}} \cdot sup_x |F_n(x) - F_m(x)|$

где $F_n(x)$ и $F_m(x)$ — эмпирические функции распределения, построенные по двум выборкам с объемами $n$ и $m$ .

Если $k_{n,m}>k_\alpha$ , то нулевая гипотеза однородности выборок отклоняется на уровне значимости $\alpha$ .

Напишем ряд функций, позволяющих вычислить статистику критерия Колмогорова-Смирнова:

In [47]:

# Частотности
def freq(data: np.ndarray, ranges: np.ndarray) -> np.ndarray:
    return np.unique(np.digitize(data, ranges), return_counts=True)[1]

# Выборочная эмпирическая функция распределения
def samp_ecdf(data: np.ndarray, ranges: np.ndarray) -> np.ndarray:
    return np.cumsum(freq(data, ranges)) / len(data)

# Статистика критерия Колмогорова-Смирнова
def k_stat(data1: np.ndarray, data2: np.ndarray, ranges: np.ndarray) -> float:
    n, m = len(data1), len(data2)
    F1, F2 = samp_ecdf(data1, ranges), samp_ecdf(data2, ranges)
    return Dn(F1, F2) * np.sqrt(n * m) / (n + m)

Вычислим статистику критерия Колмогорова-Смирнова:

In [48]:

print(f"Статистика критерия Колмогорова-Смирнова = {k_stat(sample_1, sample_2, intervals):.3f}")

Статистика критерия Колмогорова-Смирнова = 0.024

Вычислим критическое значение $k_\alpha$ , воспользовавшись уже реализованной в критерии Колмогорова функцией:

In [49]:

print(f"Критическое значение k_alpha = {k_conf(confidence):.3f}")

Критическое значение k_alpha = 1.358

Таким образом, неравенство $k_{n,m}>k_\alpha$ не выполняется. Следовательно, нулевая гипотеза однородности двух выборок принимается.

[↑] B. На равенство дисперсий¶

Для проверки выборок на равенство дисперсий воспользуемся критерием Фишера.

Критерий Фишера (F-test): Нулевая гипотеза $H_0 : \sigma_1^2 = \sigma_2^2$ принимается на уровне значимости $\alpha$ , если выполняется неравенство:

$F\left(1-\frac{\alpha}{2};\;k_1;\;k_2\right) \leq F \leq F\left(\frac{\alpha}{2};\;k_1;\;k_2\right)$

где $k_1=n_1-1$ ; $k_2=n_2-1$ ; $n_1$ , $n_2$ — объем первой и второй выборки соответственно; $\alpha$ — уровень значимости; $F = \frac{S_1^2}{S_2^2}$ — отношение несмещенных выборочных дисперсий; $F\left(1-\frac{\alpha}{2};\;k_1;\;k_2\right)$ — верхний квантиль уровня $1-\frac{\alpha}{2}$ распределения Фишера-Снедекора (т.е. соответствует нижнему квантилю уровня $\frac{\alpha}{2}$ ); $F\left(\frac{\alpha}{2};\;k_1;\;k_2\right)$ — верхний квантиль уровня $\frac{\alpha}{2}$ распределения Фишера-Снедекора.

Вычислим статистику F-теста:

In [50]:

F = np.var(sample_1, ddof=1) / np.var(sample_2, ddof=1)

print(f"F = {F:.3f}")

F = 1.052

Рассчитаем число степеней свобод $k_1$ и $k_2$ :

In [51]:

k1 = n1 - 1
k2 = n2 - 1

Вычислим квантили распределения Фишера-Снедекора, используя встроенную в scipy.stats функцию f.ppf:

In [52]:

F1 = stats.f.ppf(confidence / 2, k1, k2)
F2 = stats.f.ppf(1 - confidence / 2, k1, k2)

print(f"F1 = {F1:.3f}", f"F  = {F:.3f}", f"F2 = {F2:.3f}", sep='\n')

F1 = 0.733
F  = 1.052
F2 = 1.372

Таким образом, неравенство $F\left(1-\frac{\alpha}{2};\;k_1;\;k_2\right) \leq F \leq F\left(\frac{\alpha}{2};\;k_1;\;k_2\right)$ выполняется. Следовательно, гипотеза о равенстве дисперсий двух выборок принимается.

[↑] C. На равенство средних¶

Дисперсии неизвестны, но равны

Выполним проверку гипотезы о равенстве средних, используя t-критерий Стьюдента при условии, что дисперсии двух величин неизвестны, но равны.

Объединим две выборки в одну и определим для неё смешанную выборочную дисперсию по формуле:

$S^2 = \frac{(n_1-1) \cdot S_1^2 + (n_2-1) \cdot S_2^2}{(n_1-1)+(n_2-1)} = \frac{(n_1-1) \cdot S_1^2 + (n_2-1) \cdot S_2^2}{n_1+n_2-2}$

где $S_1^2$ и $S_2^2$ — несмещенные оценки дисперсий двух величин.

In [53]:

mixed_var = ((n1 - 1)*np.var(sample_1, ddof=1) + (n2 - 1)*np.var(sample_2, ddof=1)) / (n1 + n2 - 2)

print(f"Смешанная выборочная дисперсия S2 = {mixed_var:.3f}")

Смешанная выборочная дисперсия S2 = 950.326

Для проверки гипотезы $H_0$ вычислим значение статистики Стьюдента:

$t_{n_1+n_2-2} = \frac{\overline{x} - \overline{y}}{\sqrt{\frac{S^2}{n_1} + \frac{S^2}{n_2}}} = \frac{\overline{x} - \overline{y}}{S\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}$

In [54]:

t = (np.mean(sample_1) - np.mean(sample_2)) / np.sqrt(mixed_var / n1 + mixed_var / n2)
print(f't = {t:.4f}')

t = 0.3470

Далее вычислим $p\_value$ для полученного значения:

In [55]:

p_value = 2 * (1 - stats.t.cdf(t, n1 + n2 - 2))

print(f"p_value = {p_value:.3f}")

p_value = 0.729

Таким образом, неравенство $p\_value > \alpha$ выполняется. Следовательно, нулевая гипотеза о равенстве средних двух выборок не отвергается.

Проверим вычисления с использованием встроенной в scipy.stats функции ttest_ind:

In [56]:

_, p_value = stats.ttest_ind(sample_1, sample_2)

print(f"p_value = {p_value:.3f}")

p_value = 0.729

Математические методы машинного обучения. Контрольная работа

Оглавление:¶

[↑] Импортирование библиотек¶

[↑] Настройка отображения¶

[↑] Исходная выборка¶

[↑] 1. Статистики выборки x1,…,xnx_1, \ldots, x_n:¶

[↑] A. Среднее:¶

[↑] a. Арифметическое¶

[↑] b. Гармоническое¶

[↑] c. Геометрическое¶

[↑] B. Медиана¶

[↑] C. Мода¶

[↑] D. Нижний и верхний 0,050,05-квантиль, квартили Q1,Q2,Q3Q_1, Q_2, Q_3, интерквартильный размах¶

[↑] E. Выборочная дисперсия:¶

[↑] a. Несправленная (смещенная)¶

[↑] b. Исправленная (несмещенная)¶

[↑] F. Стандартное отклонение¶

[↑] G. Стандартная ошибка среднего¶

[↑] H. Коэффициент вариации¶

[↑] I. Моменты распределения¶

[↑] J. Коэффициент ассиметрии¶

[↑] K. Коэффициент эксцесса¶

[↑] 2. Диаграмма Box-whiskers, определение выбросов¶

[↑] 3. Интервальный ряд c использованием формулы Стёрджеса¶

[↑] 4. График эмпирической функции распределения FnF_n¶

[↑] 5. Проверка распределения на нормальность:¶

[↑] A. Гистограмма¶

[↑] B. QQ-plot¶

[↑] С. Критерий ассиметрии и эксцесса¶

[↑] D. Проверка гипотез¶

[↑] E. Критерий согласия хи-квадрат Пирсона¶

[↑] F. Критерий Колмогорова¶

[↑] 6. Проверка первых 10 значений на нормальность, используя критерий Шапиро-Уилка¶

[↑] 7. 95%95\%-й доверительный интервал для неизвестной генеральной дисперсии¶

[↑] 8. 95%95\%-й доверительный интервал для неизвестного генерального среднего при условии, что:¶

[↑] A. Генеральные дисперсии известны¶

[↑] B. Генеральные дисперсии неизвестны¶

[↑] 9. Разбиение выборки на 2 непересекающиеся группы в пропорции 55/4555/45 в произвольном порядке и проверка групп:¶

[↑] A. На однородность с использованием критерия Колмогорова-Смирнова¶

[↑] B. На равенство дисперсий¶

[↑] C. На равенство средних¶

[↑] Источники:¶

[↑] 1. Статистики выборки $x_1, \ldots, x_n$ :¶

[↑] D. Нижний и верхний $0,05$ -квантиль, квартили $Q_1, Q_2, Q_3$ , интерквартильный размах¶

[↑] 4. График эмпирической функции распределения $F_n$ ¶

[↑] 7. $95\%$ -й доверительный интервал для неизвестной генеральной дисперсии¶

[↑] 8. $95\%$ -й доверительный интервал для неизвестного генерального среднего при условии, что:¶

[↑] 9. Разбиение выборки на 2 непересекающиеся группы в пропорции $55/45$ в произвольном порядке и проверка групп:¶