Magasabb rendű probléma elemzések scipy használata ...¶
Az alábbi notebookban megismerkedünk két témával, melyek annak ellenére, hogy magukban is fontos jelentőséggel bírnak, kulcsfontosságú szerepet töltenek be más problémák numerikus megoldásában.
A numerikus integrálás témakörében megvizsgálunk néhány egyszerű integrált a scipy csomag quad függvényével.
A második kérdéskör, a differenciálegyenletek megoldása számos fizikai probléma vizsgálatában nyújthat segítséget.
Gondoljunk csak arra, hogy a klasszikus mechanika Newton törvényei, az elektrodinamika Maxwell-egyenletei, a kvantummechanika Schrödinger-egyenlete, illetve az általános relativitáselmélet Einstein-egyenletei
Numerikus integrálás¶
Sok gyakorlati alkalmazásban előkerül egy fügvény integráljának, azaz a függvény görbéje alatti területnek a meghatározása. Sok analitikus függvény integrálját zárt alakban meg lehet határozni. A gyakorlatban viszont sokszor nem ismert a függvény analitikus alakja. Gondoljunk itt például egy zajos mérésre. Ilyen esetben a függvény integrálját a rendelkezésre áló mérési pontok $x_0,x_1,x_2,…x_j,…$ és mért értékek $f_0,f_1,f_2,…f_j,…$ alapján kell valahogy meghatároznunk. Ekkor az integrál értékét rendszerint egy véges összegzéssel határozhatjuk meg, ahol az összeadandó értékek a mérési pontok és a mért mennyiségek valamilyen függvényei. Az alábbiakban a scipy csomag quad függvényével fogunk megismerkedni, mely függvények numerikus integrálására alkalmas.
1D integrál¶
# a szokásos rutinok betöltése
%pylab inline
from scipy.integrate import * # az integráló rutinok betöltése
Populating the interactive namespace from numpy and matplotlib
Vizsgáljuk meg az alábbi egyszerű integrált $$ \int_{-1}^1 (x^2+3x +2)\mathrm{d}x .$$
Ennek az értéke némi algebrával $14/3\approx 4.66666$ Vajon ugyen ezt kapjuk-e a quad fügvénnyel ?
Először definiáljuk az integrálandó függvényt.
def f(x):
return (x**2+3*x+2)
Most már meghívhatjuk a quad-ot. Az első változó az integrálandó függvény, a második és a harmadik pedig az integrálási határok. A kimenet két szám. Az első az integrál becsült értéke, a második az algoritmus becsült hibája.
quad(f,-1,1)
(4.666666666666666, 5.1810407815840634e-14)
Amint az eredmény is mutatja, ez az analitikus számítás és a numerikus integrál megegyeznek.
Előfordulhat, hogy az integrálási határok végtelenek. Például vizsgáljuk meg a Gauss-görbe alatti területet: $$ \int_{-\infty}^\infty \mathrm{e}^{-x^2}\mathrm{d}x =\sqrt{\pi}$$
# az integrandus definiálása
def gauss(x):
return exp(-x**2)
A quad függvénynek a végtelen integrálási határokat az inf jelöléssel adhatjuk meg.
quad(gauss,-inf,inf)
(1.7724538509055159, 1.4202636781830878e-08)
sqrt(pi)
1.7724538509055159
A fent vizsgált két példával különösebb gond nélkül meg tudott birkózni a quad. Előfordul azonban, hogy az integrálás problémákba ütközik. Erre egy jó példa, ha az integrandus szingulárissá válik a integrálási tartomány egy pontjában. Ez nem feltétlenül jelenti azt, hogy az integrál nem létezik! Az ilyen pontokra külön felhívhatjuk a quad függvény figyelmét a points kulcsszó segítségével.
Vizsgáljuk meg a $$h(x)=\sqrt[3]{\frac{1}{(x-1)^2}}$$ függvényt mely a $x=1$ esetén divergál:
def h(x):
return ((x-1.0)**(-2))**(1.0/3.0)
quad(h,0,2)
--------------------------------------------------------------------------- ZeroDivisionError Traceback (most recent call last) <ipython-input-8-be7543cb4b00> in <module> ----> 1 quad(h,0,2) ~\Anaconda3\lib\site-packages\scipy\integrate\quadpack.py in quad(func, a, b, args, full_output, epsabs, epsrel, limit, points, weight, wvar, wopts, maxp1, limlst) 339 if weight is None: 340 retval = _quad(func, a, b, args, full_output, epsabs, epsrel, limit, --> 341 points) 342 else: 343 retval = _quad_weight(func, a, b, args, full_output, epsabs, epsrel, ~\Anaconda3\lib\site-packages\scipy\integrate\quadpack.py in _quad(func, a, b, args, full_output, epsabs, epsrel, limit, points) 446 if points is None: 447 if infbounds == 0: --> 448 return _quadpack._qagse(func,a,b,args,full_output,epsabs,epsrel,limit) 449 else: 450 return _quadpack._qagie(func,bound,infbounds,args,full_output,epsabs,epsrel,limit) <ipython-input-7-883f538cfcc5> in h(x) 1 def h(x): ----> 2 return ((x-1.0)**(-2))**(1.0/3.0) ZeroDivisionError: 0.0 cannot be raised to a negative power
A quad bizony nehézségekbe ütközik, ha a 0 reciprokát kell vennie! Specifikáljuk most az $x=1$-et mint problémás pontot:
quad(h,0,2,points=[1.0])
(6.000000000001058, 4.787281682183675e-12)
Így az integrál már szépen elvégezhető.
2D integrál¶
A quad függvény kétdimenziós változata a dblquad. Nézzünk két egyszerű példát kétdimenziós integrálra is!
Integráljuk a $$ \cos(x) e^{-(x^2+y^2)} $$ függvényt az alábbi két integrálási tartományon:
- egy origó központú egységnyi hosszú négyzeten
- az origó központú egység körlapon!
# Az integrandus definiálása
def func(x,y):
return cos(x)*exp(-x**2-y**2)
A dblquad első paramétere megint az integrálandó függvény. A második és harmadik bemenő paraméter az integrandusfüggvény első paraméterének határait adja meg. A negyedik és ötödik bemenő paraméter az első integrálási változó függvényeként kifejezve a második integrálási változó határai. A legegyszerűbb esetben ezek valamilyen konstansfüggvények.
Az első integrálási tartomány tehát így számítható :
dblquad(func, -1/2, 1/2, lambda x:-1/2, lambda x:1/2)
(0.8183636555228812, 9.085661728779128e-15)
A második integrálási tartományban az $x$ változó függvényében kell paraméterezni az $y$ változó szélső értékeit. Ha az integrálási tartomány az egység sugarú körlap, akkor az alsó határt a $y(x)=-\sqrt{1-x^2}$, a felső határt pedig a $y(x)=\sqrt{1-x^2}$ adja:
dblquad(func,-1,1,lambda x:-sqrt(1-x**2),lambda x:sqrt(1-x**2))
(1.7860608962993605, 2.211336003199449e-09)
Differenciálegyenletek¶
Amint azt a bevezetőben is említettük, a fizikai törvények jelentős része a differenciálegyenletek nyelvén van megfogalmazva.
Az alábbiakban megismerkedünk az odeint rutinnal amely differenciálegyenletek numerikus megoldását tesz lehetővé.
from scipy.integrate import * # ez kell a diffegyenletekhez is!!
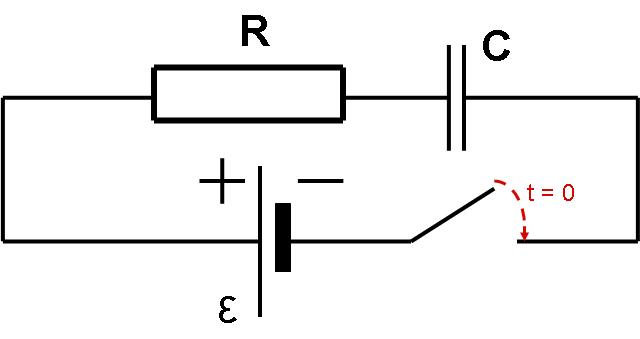
Egy egyenletet differenciálegyenletnek hívunk, ha a meghatározandó függvény deriváltjai szerepelnek benne. Egy egyszerű differenciálegyenletre jutunk például, ha megvizsgáljuk egy kondenzátor töltésének időbeli válltozását!
A kondenzátoron felhalmozott $Q$ töltés meghatározására induljunk ki a Kirchhoff-féle huroktörvényből, amit a fenti ábrán látható áramkörre írtunk fel: $$ \varepsilon= \underbrace{I R}_{U_R}+ \underbrace{\frac{Q}{C}}_{U_C} = \frac{\mathrm{d}Q}{\mathrm{d}t}R+\frac{Q}{C}$$
A megoldandó differenciálegyenlet tehát:
$$ \frac{\mathrm{d}Q}{\mathrm{d}t}= \frac{\varepsilon}{R}-\frac{Q}{RC} $$Tegyük fel, hogy a kezdetben üres volt a kondenzátor, tehát $Q(0)=0$, és számoljunk az $\varepsilon=1\mathrm{V}$, $R=1\mathrm{M}\Omega$ és $C=100nF$ paraméterekkel!
# Paraméterek definiálása
epsilon=1
R=1.0e6
C=1.0e-7
Az odeint függvény hívásához szükség van a paramétereken kívül a növekményfüggvényre (azaz a fenti egyenlet jobb oldalára), definiáljuk most ezt:
def RCkor(q,t):
return epsilon/R-q/(R*C)
Most már készen vagyunk arra, hogy meghívjuk a differenciál egyenlet megoldó függvényt! Az odeint alapvetően három bemenő paramétert vár. Az első a fent definiált növekményfüggvény, a második a meghatározandó függvény kezdeti értéke, a harmadik pedig azon időpontok halmaza, ahol kíváncsiak vagyunk a megoldásra. A függvény visszatérési értéke maga a keresett adatsor.
t=linspace(0,1,1000) # ezek az érdekes idő pillanatok
q0=0 # A töltés kezdeti értéke
q=odeint(RCkor,q0,t) # itt oldjuk meg a diffegyenletet
--------------------------------------------------------------------------- NameError Traceback (most recent call last) <ipython-input-12-19d242771254> in <module> 1 t=linspace(0,1,1000) # ezek az érdekes idő pillanatok 2 q0=0 # A töltés kezdeti értéke ----> 3 q=odeint(RCkor,q0,t) # itt oldjuk meg a diffegyenletet ~\Anaconda3\lib\site-packages\scipy\integrate\odepack.py in odeint(func, y0, t, args, Dfun, col_deriv, full_output, ml, mu, rtol, atol, tcrit, h0, hmax, hmin, ixpr, mxstep, mxhnil, mxordn, mxords, printmessg, tfirst) 242 full_output, rtol, atol, tcrit, h0, hmax, hmin, 243 ixpr, mxstep, mxhnil, mxordn, mxords, --> 244 int(bool(tfirst))) 245 if output[-1] < 0: 246 warning_msg = _msgs[output[-1]] + " Run with full_output = 1 to get quantitative information." <ipython-input-11-9c74ebed5d0e> in RCkor(q, t) 1 def RCkor(q,t): ----> 2 return epsilon/R-q/(R*C) NameError: name 'epsilon' is not defined
Most már csak ábrázolni kell!
plot(t,q/C,lw=3)
xlabel(r'$t$[s]',fontsize=20)
ylabel(r'$Q/C$[V]',fontsize=20)
grid()
--------------------------------------------------------------------------- NameError Traceback (most recent call last) <ipython-input-10-23b0be4607c9> in <module> ----> 1 plot(t,q/C,lw=3) 2 xlabel(r'$t$[s]',fontsize=20) 3 ylabel(r'$Q/C$[V]',fontsize=20) 4 grid() NameError: name 't' is not defined
Vizsgáljunk meg egy másik példát ! Legyen ez egy rugóval rögzített test, mely egy vonal mentén súrlódás nélkül tud mozogni.
Ennek a mozgásnak az egyenlete Newton szerint,
$$m\frac{\mathrm{d}^2x}{\mathrm{d}t^2}(t)=-kx(t)$$Írjuk át ezt az időben másodrendű differenciálegyenletet két időben elsőrendű differenciálegyenletre!
$$\frac{\mathrm{d}x}{\mathrm{d}t}(t)=v(t)$$$$m \frac{\mathrm{d}v}{\mathrm{d}t}(t)=-k x(t)$$Általában minden magasabb rendű differenciálegyenlet rendje hasonló módon csökkenthető. Azaz a legáltalánosabb esetben is új ismeretlen függvények bevezetésével elsőrendű differenciálegyenlet-rendszer megoldására tudjuk redukálni a problémánkat!
Vizsgáljuk meg azt az esetet, ha $m=k=1$ ! Most a növekményfüggvényünk egy kételemű vektort kell, hogy kezeljen!
def f(u, t):
x=u[0] # az u első komponense a kitérés
v=u[1] # az u második komponense a sebesség
return [v,-x] # ez maga a növekmény kiértékelése
Oldjuk meg az egyenleteket úgy, hogy kezdetben a kitérés 1, a kezdősebesség pedig nulla!
t=linspace(0,20,1000); # az idő intervallum
u0 = [1,0] # kezdeti érték x-re és v-re
u=odeint(f,u0,t) # itt történik a diffegyenlet megoldása
plot(t,u[:,0],label=r'$x(t)$ pozicio')
plot(t,u[:,1],label=r'$v(t)$ sebesseg')
legend(fontsize=20)
xlabel(r'$t$[s]',fontsize=20)
grid()