Transformation between internal and cartesian coordinates¶
import pandas as pd
import chemcoord as cc
water = cc.Cartesian.read_xyz("water_dimer.xyz", start_index=1)
zwater = water.get_zmat()
small = cc.Cartesian.read_xyz("MIL53_small.xyz", start_index=1)
Naming convention¶
The table which defines the used references of each atom will be called construction table.
The contruction table of the zmatrix of the water dimer can be seen here:
zwater.loc[:, ["b", "a", "d"]]
| b | a | d | |
|---|---|---|---|
| 1 | origin | e_z | e_x |
| 2 | 1 | e_z | e_x |
| 3 | 1 | 2 | e_x |
| 4 | 2 | 1 | 3 |
| 5 | 4 | 2 | 1 |
| 6 | 4 | 5 | 2 |
The absolute references are indicated by magic strings: ['origin', 'e_x', 'e_y', 'e_z'].
- The atom which is to be set in the reference of three other atoms, is denoted $i$.
- The bond-defining atom is represented by $b$.
- The angle-defining atom is represented by $a$.
- The dihedral-defining atom is represented by $d$.
Mathematical introduction¶
It is advantageous to treat a zmatrix simply as recursive spherical coordinates.
The $(n + 1)$-th atom uses three of the previous $n$ atoms as reference. Those three atoms ($b, a, d$) are spanning a coordinate system, if we require righthandedness. If we express the position of the atom $i$ in respect to this locally spanned coordinate system using spherical coordinates, we arrive at the usual definition of a zmatrix.
PS: The question about right- or lefthandedness is equivalent to specifying a direction of rotation. Chemcoord uses of course the IUPAC definition.
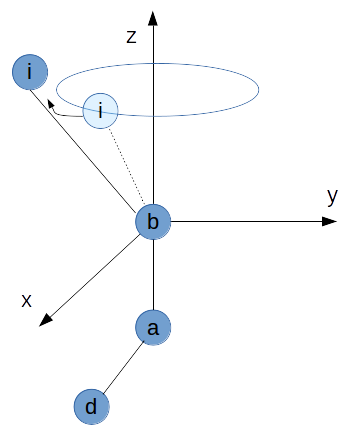
Ideal case¶
The ideal (and luckily most common) case is, that $\vec{ib}$, $\vec{ba}$, and $\vec{ad}$ are linearly independent. In this case there exist a bijective mapping between spherical coordinates and cartesian coordinates and all angles, positions... are well defined.
Linear angle¶
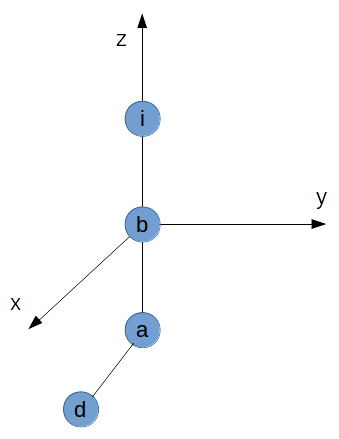
One pathologic case appears, if $\vec{ib}$ and $\vec{ba}$ are linear dependent.
This means, that the angle in the zmatrix is either $0^\circ$ or $180^\circ$. In this case there are infinitely many dihedral angles for the same configuration in cartesian space. Or to say it in a more analytical way: The transformation from spherical coordinates to cartesian coordinates is surjective, but not injective.
For nearly all cases (e.g. expressing the potential hyper surface in terms of internal coordinates), the surjectivity property is sufficient.
A lot of other problematic cases can be automatically solved by assigning a default value to the dihedral angle by definition ($0^\circ$ in the case of chemcoord).
Usually the user does not need to think about this case, which is automatically handled by chemcoord.
Linear reference¶
The real pathologic case appears, if the three reference atoms are linear.
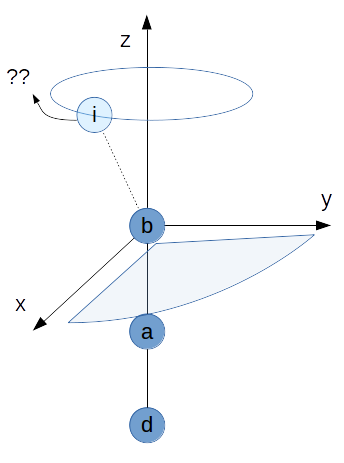
It is important to note, that this is not a problem in the spherical coordinates of i.
The coordinate system itself which is spanned by b, a and d is undefined.
This means, that it is not visible directly from the values in the Zmatrix, if i uses an invalid reference.
I will use the term valid Zmatrix if all atoms i have valid references. In this case the transformation to cartesian coordinates is well defined.
Now there are two cases:
Creation of a valid Zmatrix¶
Chemcoord asserts, that the Zmatrix which is created from cartesian coordinates using get_zmat is a valid Zmatrix (or raises an explicit exception if it fails at finding valid references.) This is always done by choosing other references (instead of introducing dummy atoms.)
Manipulation of a valid Zmatrix¶
If a valid Zmatrix is manipulated after creation, it might occur because of an assignment, that b, a, and d are moved into a linear relationship. In this case a dummy atom is inserted which lies in the plane which was spanned by b, a, and d before the assignment. It uses the same references as the atom d, so changes in the references of b, a and d are also present in the position of the dummy atom X.
This is done using the safe assignment methods of chemcoord.
Example¶
water = water - water.loc[5, ["x", "y", "z"]]
zmolecule = water.get_zmat()
c_table = zmolecule.loc[:, ["b", "a", "d"]]
c_table.loc[6, ["a", "d"]] = [2, 1]
zmolecule1 = water.get_zmat(construction_table=c_table)
zmolecule2 = zmolecule1.copy()
zmolecule3 = water.get_zmat(construction_table=c_table)
Modifications on zmolecule1¶
angle_before_assignment = zmolecule1.loc[4, "angle"]
zmolecule1.safe_loc[4, "angle"] = 180
/home/mcocdawc/code/chemcoord/src/chemcoord/internal_coordinates/_zmat_class_core.py:551: UserWarning: For the dihedral reference of atom 5 the dummy atom 7 was inserted warnings.warn(give_message(i=i, dummy_d=dummy_d), UserWarning) /home/mcocdawc/code/chemcoord/src/chemcoord/internal_coordinates/_zmat_class_core.py:551: UserWarning: For the dihedral reference of atom 6 the dummy atom 8 was inserted warnings.warn(give_message(i=i, dummy_d=dummy_d), UserWarning)
zmolecule1.safe_loc[5, "dihedral"] = 90
zmolecule1.safe_loc[4, "angle"] = angle_before_assignment
/home/mcocdawc/code/chemcoord/src/chemcoord/internal_coordinates/_zmat_class_core.py:618: UserWarning: The dummy atoms [5, 6] were removed
warnings.warn('The dummy atoms {} were removed'.format(to_remove),
xyz1 = zmolecule1.get_cartesian()
xyz1.view()
Contextmanager¶
With the following contextmanager we can switch the automatic insertion of dummy atoms of and look at the cartesian which is built after assignment of .safe_loc[4, 'angle'] = 180. It is obvious from the structure, that the coordinate system spanned by O - H - O is undefined. This was the second pathological case in the mathematical introduction.
with cc.DummyManipulation(False):
try:
zmolecule3.safe_loc[4, "angle"] = 180
except cc.exceptions.InvalidReference as e:
e.already_built_cartesian.view()
Symbolic evaluation¶
It is possible to use symbolic expressions from sympy.
import sympy
sympy.init_printing()
d = sympy.Symbol("d")
symb_water = zwater.copy()
symb_water.safe_loc[4, "bond"] = d
symb_water
| atom | b | bond | a | angle | d | dihedral | |
|---|---|---|---|---|---|---|---|
| 1 | O | origin | 0.0 | e_z | 0.000000 | e_x | 0.000000 |
| 2 | H | 1 | 0.910922 | e_z | 56.385853 | e_x | -0.000000 |
| 3 | H | 1 | 0.910922 | 2 | 107.000024 | e_x | -0.000000 |
| 4 | O | 2 | $d$ | 1 | 132.466298 | 3 | -16.755013 |
| 5 | H | 4 | 0.910922 | 2 | 132.466298 | 1 | 180.000000 |
| 6 | H | 4 | 0.910922 | 5 | 107.000024 | 2 | 163.244987 |
symb_water.subs(d, 2)
| atom | b | bond | a | angle | d | dihedral | |
|---|---|---|---|---|---|---|---|
| 1 | O | origin | 0.000000 | e_z | 0.000000 | e_x | 0.000000 |
| 2 | H | 1 | 0.910922 | e_z | 56.385853 | e_x | -0.000000 |
| 3 | H | 1 | 0.910922 | 2 | 107.000024 | e_x | -0.000000 |
| 4 | O | 2 | 2.000000 | 1 | 132.466298 | 3 | -16.755013 |
| 5 | H | 4 | 0.910922 | 2 | 132.466298 | 1 | 180.000000 |
| 6 | H | 4 | 0.910922 | 5 | 107.000024 | 2 | 163.244987 |
cc.xyz_functions.view([symb_water.subs(d, i).get_cartesian() for i in range(2, 5)])
# If your viewer cannot open molden files you have to uncomment the following lines
# for i in range(2, 5):
# symb_water.subs(d, i).get_cartesian().view()
# time.sleep(1)
Definition of the construction table¶
The construction table in chemcoord is represented by a pandas DataFrame with the columns ['b', 'a', 'd'] which can be constructed manually.
pd.DataFrame([[1, 2, 3], [4, 5, 6], [7, 8, 9]], columns=["b", "a", "d"])
| b | a | d | |
|---|---|---|---|
| 0 | 1 | 2 | 3 |
| 1 | 4 | 5 | 6 |
| 2 | 7 | 8 | 9 |
It is possible to specify only the first $i$ rows of a Zmatrix, in order to compute the $i + 1$ to $n$ rows automatically. If the molecule consists of unconnected fragments, the construction tables are created independently for each fragment and connected afterwards. It is important to note, that an unfragmented, monolithic molecule is treated in the same way. It just consists of one fragment. This means that in several methods where a list of fragments is returned or taken, an one element list appears.
If the Zmatrix is automatically created, the oxygen 1 is the first atom. Let's assume, that we want to change the order of fragments.
water.get_zmat()
| atom | b | bond | a | angle | d | dihedral | |
|---|---|---|---|---|---|---|---|
| 1 | O | origin | 3.825100 | e_z | 97.575672 | e_x | -172.422536 |
| 2 | H | 1 | 0.910922 | e_z | 13.716615 | e_x | -146.597056 |
| 3 | H | 1 | 0.910922 | 2 | 107.000024 | e_x | -12.723783 |
| 4 | O | 2 | 2.351206 | 1 | 132.466298 | 3 | -16.755013 |
| 5 | H | 4 | 0.910922 | 2 | 132.466298 | 1 | -180.000000 |
| 6 | H | 4 | 0.910922 | 5 | 107.000024 | 2 | 163.244987 |
Let's fragmentate the water
fragments = water.fragmentate()
c_table = water.get_construction_table(fragment_list=[fragments[1], fragments[0]])
water.get_zmat(c_table)
| atom | b | bond | a | angle | d | dihedral | |
|---|---|---|---|---|---|---|---|
| 4 | O | origin | 0.910922 | e_z | 123.614147 | e_x | -180.000000 |
| 5 | H | 4 | 0.910922 | e_z | 29.624299 | e_x | -0.000000 |
| 6 | H | 4 | 0.910922 | 5 | 107.000024 | e_x | -0.000000 |
| 2 | H | 4 | 2.351206 | 6 | 118.561123 | 5 | 165.988232 |
| 1 | O | 2 | 0.910922 | 4 | 132.466298 | 6 | 18.293238 |
| 3 | H | 1 | 0.910922 | 2 | 107.000024 | 4 | -16.755013 |
If we want to specify the order in the second fragment, so that it connects via the oxygen 1, it is important to note, that we have to specify the full row. It is not possible to define just the order without the references.
frag_c_table = pd.DataFrame(
[[4, 6, 5], [1, 4, 6], [1, 2, 4]], columns=["b", "a", "d"], index=[1, 2, 3]
)
c_table2 = water.get_construction_table(
fragment_list=[fragments[1], (fragments[0], frag_c_table)]
)
water.get_zmat(c_table2)
| atom | b | bond | a | angle | d | dihedral | |
|---|---|---|---|---|---|---|---|
| 4 | O | origin | 0.910922 | e_z | 123.614147 | e_x | -180.000000 |
| 5 | H | 4 | 0.910922 | e_z | 29.624299 | e_x | -0.000000 |
| 6 | H | 4 | 0.910922 | 5 | 107.000024 | e_x | -0.000000 |
| 1 | O | 4 | 3.041381 | 6 | 106.381653 | 5 | 170.133373 |
| 2 | H | 1 | 0.910922 | 4 | 34.769425 | 6 | -163.300710 |
| 3 | H | 1 | 0.910922 | 2 | 107.000024 | 4 | -16.755013 |