# Importing Python modules required for this notebook
# (this cell must be executed with "shift+enter" before any other Python cell)
import numpy as np
import matplotlib.pyplot as plt
from MRPy import *
Questão 1¶
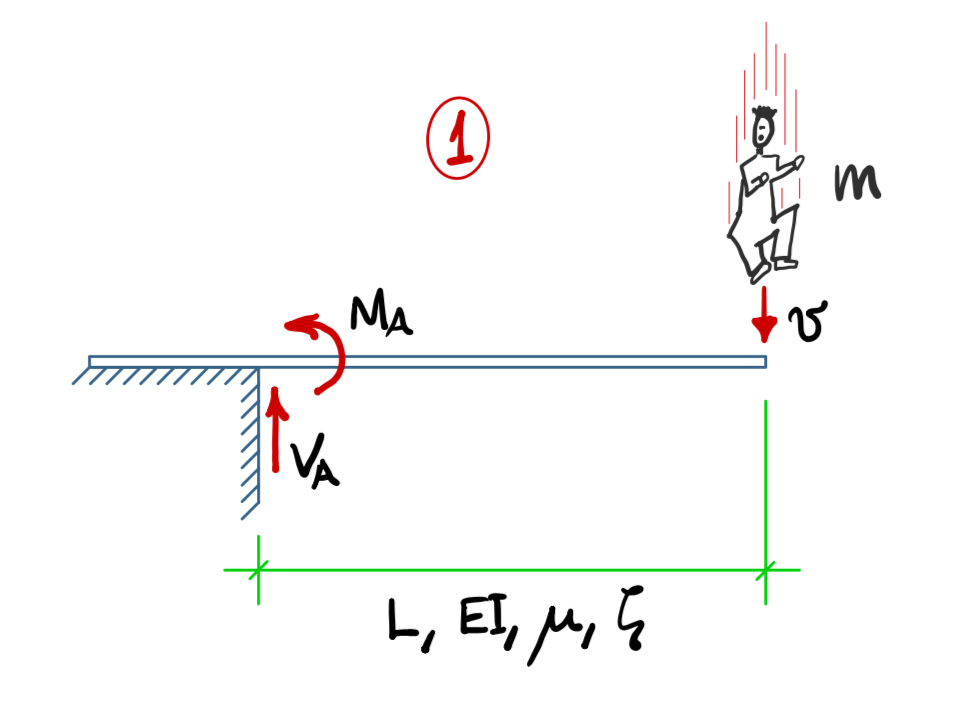
Uma pessoa com massa $m = 80$kg impacta verticalmente a extremidade de um trampolim com velocidade $v = 3$m/s. O trampolim tem comprimento $L = 2$m, massa por unidade de comprimento $\mu = 20$kg/m, e amortecimento $\zeta = 2$% (razão do crítico). A rigidez à flexão, $EI$, é tal que o deslocamento estático sob o peso da pessoa é 0,1m. Pergunta-se:
- Qual o máximo deslocamento na extremidade do trampolim após o impacto?
- Qual o tempo transcorrido até que a pessoa perca o contato com o trampolim ao ser projetada de volta para cima?
- Quantos ciclos de vibração o trampolim completará antes que a pessoa volte a cair impactando o mesmo pela segunda vez?
- Quais as máximas reações de apoio $M_A$ (momento) e $V_A$ (força vertical)?
Cálculo das propriedades do sistema¶
L = 2. # comprimento do trampolim (m)
vp = 3. # velocidade da pessoa no contato (m/s)
mp = 80. # massa da pessoa (kg)
mt = 20*L/2 # massa do trampolim (metade da massa total, kg)
m = mp + mt # massa oscilante total (kg)
zt = 0.02 # amortecimento razão do crítico
ue = 0.1 # deslocamento estático sob o peso da pessoa (m)
g = 9.81 # gravidade (m/s2)
k = mp*g/ue # coeficiente de rigidez
Q = mp*vp # quantidade de movimento inicial
v0 = Q/m # velocidade pessoa+trampolim após contato
wn = np.sqrt(k/m) # frequência natural (rad/s)
fn = wn/2/np.pi # frequência natural (Hz)
print('Rigidez do trampolim: {0:5.0f} N/m'.format(k))
print('Massa total (pessoa + trampolim): {0:5.1f} kg'.format(m))
print('Velocidade inicial (pessoa + trampolim): {0:5.2f} m/s'.format(v0))
print('Frequência natural do sistema: {0:5.2f} Hz'.format(fn))
Rigidez do trampolim: 7848 N/m Massa total (pessoa + trampolim): 100.0 kg Velocidade inicial (pessoa + trampolim): 2.40 m/s Frequência natural do sistema: 1.41 Hz
1) Deslocamento máximo¶
Após o contato, a massa da pessoa se soma à massa (parcial) do trampolim com uma velocidade inicial dada. O deslocamento máximo tem duas parcelas:
- um deslocamento devido a uma velocidade inicial, mais
- um deslocamento devido a uma força impulsiva retangular de duração infinita, com fator de amplificação A = 2.

Na verdade esses dois deslocamentos de pico não acontecerão exatamente no mesmo instante e, portanto, simplesmente somá-los é uma simplificação que resulta em um deslocamento total superestimado. Além disso, ao se desprezar o efeito do amortecimento na amplitude observada após 1/4 do período, o deslocamento máximo devido à velocidade inicial também é um pouco superestimado.
umax_1 = v0/wn # parcela referente à conservação da quantidade de moviment
umax_2 = 2*ue # parcela referente à força impulsiva
umax = umax_1 + umax_2
print('Deslocamento devido à velocidade inicial: {0:5.2f} m'.format(umax_1))
print('Deslocamento devido à força impulsiva: {0:5.2f} m'.format(umax_2))
print('Deslocamento máximo total: {0:5.2f} m'.format(umax))
Deslocamento devido à velocidade inicial: 0.27 m Deslocamento devido à força impulsiva: 0.20 m Deslocamento máximo total: 0.47 m
O cálculo abaixo, obviamente não exigido na prova, apresenta o resultado correto para essa questão utilizado uma integração por Duhamel.
F = MRPy(-mp*g*np.ones((1,1024)), Td=8)/m # força constante a partir de t = 0
u = F.sdof_Duhamel(fn, zt, V0=-v0) # resolve por Duhamel, com velocidade inicial dada
u.plot_time(fig=2, figsize=[10,4], axis_t=[0, u.Td, -0.6, 0.6]);
u_pk = np.max(np.abs(u[0]))
print('Deslocamento máximo total (por Duhamel): {0:5.2f} m'.format(u_pk))
Deslocamento máximo total (por Duhamel): 0.38 m
O que confirma que a simples superposição dos dois efeitos superestima o pico de deslocamento.
2) Tempo até nova perda de contato¶
A resposta devida à velocidade inicial reverte o sinal e é maior que a resposta devida à força impulsiva, que não reverte o sinal. Portanto a resposta total terá reversão de sinal, como de fato pode ser observado no gráfico da solução por Duhamel.
Pode-se então supor que o contato só será desfeito no momento em que o deslocamento atinge o pico com o sinal revertido, o que ocorre mais ou menos aos 3/4 do período natural de vibração livre do sistema pessoa+trampolim.
Tn = 1/fn # período de vibração (pessoa + trampolim)
tk1 = 3*Tn/4 # perda de contato estimada
t = u.t_axis() # perda de contato pela solução por Duhamel
kt = np.argmax(u[0])
tk2 = t[kt]
print('A perda de contato ocorrerá aos {0:5.3f} s'.format(tk1))
print('Pela solução por Duhamel seria aos {0:5.3f} s'.format(tk2))
A perda de contato ocorrerá aos 0.532 s Pela solução por Duhamel seria aos 0.571 s
Portanto o critério usado para a estimativa é razoável.
band = [2/u.Td, u.fs/32]
a = u.differentiate(band=band).differentiate(band=band)
a.plot_time(fig=2, figsize=[10,4], axis_t=[0, a.Td/2, -40, 40]);
3) Trampolim sem a pessoa¶
A partir do momento em que o trampolim está oscilando sem a pessoa sua frequência natural aumenta, porque embora a rigidez permaneça a mesma a massa aderida diminui.
wnt = np.sqrt(k/mt)
fnt = wnt/2/np.pi
Tnt = 1/fnt
print('Período de vibração pessoa+trampolin: {0:5.2f} s'.format(Tn))
print('Período de vibração só trampolim: {0:5.2f} s'.format(Tnt))
Período de vibração pessoa+trampolin: 0.71 s Período de vibração só trampolim: 0.32 s
Portanto o período reduz-se para aproximadamente a metade.
Considerando que houve uma restituição total da energia cinética, a velocidade da pessoa ao se soltar do trampolim é a mesma do instante de contato inicial.
O tempo para retornar ao contato é dado pela equação da posição de um corpo acelerado:
$$ u = u_0 + v_0 t + \frac{a t^2}{2} $$com $u = u_0$ (retorno à mesma posição inicial) e $a = g$. Isolando-se $t$ tem-se:
$$ t = \frac{2v_0}{g}$$onde $v_0$ é a velocidade da pessoa no momento do contato inicial (3m/s). Dividindo-se o tempo transcorrido pelo período do trampolim vazio tem-se então:
T1 = 2*vp/g
N = T1/Tnt
print('Tempo até novo contato: {0:5.2f} s'.format(T1))
print('Número aprox. de oscilações do trampolim: {0:7.0f}'.format(np.round(N)))
Tempo até novo contato: 0.61 s Número aprox. de oscilações do trampolim: 2
4) Máximas reações de apoio¶
As máximas reações podem ser estimadas a partir da força estática equivalente. Para isso, vamos usar o deslocamento máximo (superestimado) do item (1).
Feq = umax*k # força estática equivalente
MA = L*Feq # momento reativo
VA = Feq # reação vertical
print('Momento reativo no engaste: {0:5.0f} Nm'.format(MA))
print('Reação vertical no engaste: {0:5.0f} N'.format(VA))
Momento reativo no engaste: 7391 Nm Reação vertical no engaste: 3696 N
Contudo, o valor correto calculado a partir da solução por Duhamel (não exigida na prova) seria:
Feq = u_pk*k # força estática equivalente
MA = L*Feq # momento reativo
VA = Feq # reação vertical
print('Momento reativo no engaste: {0:5.0f} Nm'.format(MA))
print('Reação vertical no engaste: {0:5.0f} N'.format(VA))
Momento reativo no engaste: 5949 Nm Reação vertical no engaste: 2974 N
Questão 2¶
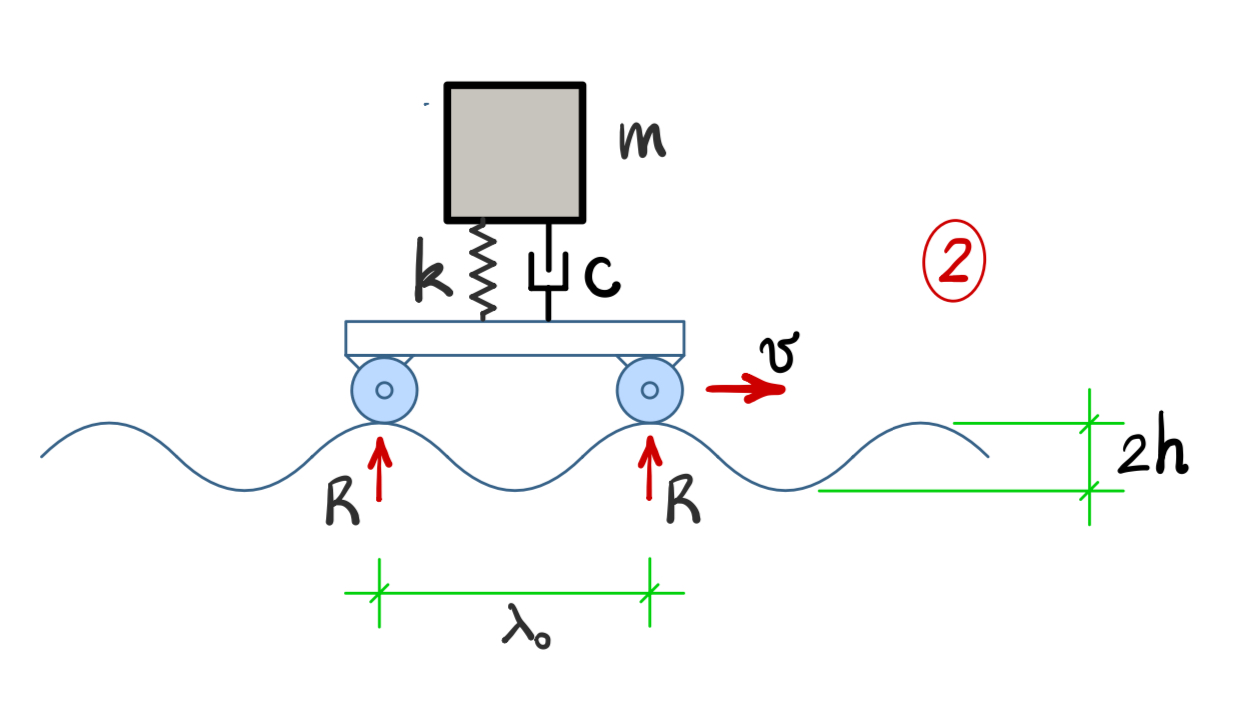
Um carrinho se desloca com velocidade estacionária $v$ sobre uma superfície com relevo senoidal, cujo comprimento de onda (igual à distância entre as rodas) é $\lambda_0 = 2$m e amplitude (zero-a-pico) $h = 0,1$m. Sobre o carrinho é transportada uma massa $m = 200$kg, que está suportada por um console elástico cujo amortecimento é $\zeta = 1$% (razão do crítico). Considere que a massa do carrinho é desprezável.
- Admitindo inicialmente um console rígido, qual a máxima velocidade $v_{\rm MAX}$ que o carrinho pode atingir antes que as rodas percam contato com a superfície.
- Para $v = v_{\rm MAX}/2$, determine a rigidez da mola k de modo que a amplitude total de vibração da massa (zero-a-pico) seja no máximo igual a $2h$.
- Para a rigidez $k$ calculada, determine a máxima e a mínima forças de reação vertical $R$ em cada roda durante o movimento.
Cálculo das propriedades do sistema¶
h = 0.1 # amplitude do deslocamento na base
l0 = 2. # distância entre rodas (m)
m = 200. # massa oscilante total (kg)
zt = 0.01 # amortecimento razão do crítico
g = 9.81 # gravidade (m/s2)
2.1 Velocidade máxima¶
Com a mola considerada rígida, a massa acompanha o relevo do terreno. Isso implica em um deslocamento da base igual ao deslocamento da massa com uma frequência igual a $f_0 = v_{\rm max}/\lambda_0$. O deslocamento vertical é uma função harmônica:
$$ u(t) = h \sin (2\pi f_0 t) = h \sin \left( \frac{2\pi v_{\rm max} t}{\lambda_0} \right) $$O critério para que o carrinho não descole do terreno é a aceleração vertical não superar a gravidade. A aceleração é a segunda derivada do deslocamento.
$$ a = \frac{d^2 u}{dt^2} = - h \left(\frac{2\pi v_{\rm max}}{\lambda_0} \right)^2 \sin \left( \frac{2\pi v_{\rm max} t}{\lambda_0} \right) > -g $$Portanto o limite de velocidade é dado por:
$$ h \left(\frac{2\pi v_{\rm max}}{\lambda_0} \right)^2 = g $$Que resulta em:
$$ v_{\rm max} = \frac{\lambda_0}{2\pi} \sqrt{\frac{g}{h}}$$vmax = (l0/2/np.pi)*np.sqrt(g/h)
print('Máxima velocidade para manter contato: {0:5.2f} m/s'.format(vmax))
Máxima velocidade para manter contato: 3.15 m/s
2.2 Amplitude de vibração para velocidade $v_{\rm max}/2$¶
A aceleração na base é dada pela mesma expressão anterior, mas com a velocidade agora reduzida à metade:
$$ a = - h \left(\frac{\pi v_{\rm max}}{\lambda_0} \right)^2 \sin \left( \frac{\pi v_{\rm max} t}{\lambda_0} \right)$$onde a frequência de excitação é dada por:
$$ f_0 = \frac{\pi v_{\rm max}}{2\pi \cdot \lambda_0} = \frac{v_{\rm max}}{2\lambda_0} $$Calculando amplitude e frequência da excitação:
aG = h*((np.pi*vmax/l0)**2)
f0 = vmax/(2*l0)
print('Amplitude da aceleração: {0:5.2f} m/s2'.format(aG))
print('Frequência da excitação harmônica: {0:5.2f} Hz'.format(f0))
Amplitude da aceleração: 2.45 m/s2 Frequência da excitação harmônica: 0.79 Hz
Para que a amplitude total seja no máximo $2h$, a amplitude do sistema deve ser no máximo $h$, visto que já ocorre uma amplitude $h$ inerente ao próprio relevo.
No cálculo a seguir, vamos variando a frequência $f_{\rm n}$ até ter a amplitude de deslocamento desejada:
fn = 1.414*f0 # valor obtido por tentativa e erro
k = ((2*np.pi*fn)**2)*m
ue = aG*m/k
bt = f0/fn
A = np.sqrt(1/((1 - bt**2)**2 + (2*zt*bt)**2))
ud = A*ue
print('Frequência natural de vibração livre: {0:5.3f} Hz'.format(fn))
print('Resposta em deslocamento estático: {0:5.3f} m'.format(ue))
print('AMPLITUDE DA RESPOSTA EM DESLOCAMENTO: {0:5.3f} m'.format(ud))
print('Fator de amplificação dinâmica: {0:5.3f}'.format(A))
print('Rigidez calibrada: {0:5.3f} kN/m'.format(k/1000))
Frequência natural de vibração livre: 1.114 Hz Resposta em deslocamento estático: 0.050 m AMPLITUDE DA RESPOSTA EM DESLOCAMENTO: 0.100 m Fator de amplificação dinâmica: 2.000 Rigidez calibrada: 9.807 kN/m
2.3 Máxima reação vertical¶
A máxima amplitude de deslocamento é portanto $h$, que multiplicada pela rigidez dá a força da mola sobre a massa. Essa força deve ser ainda ser acrescida do peso da massa (quando a roda passa pelo ponto mais baixo) e dividida entre os dois eixos. Portanto:
R = (h*k + m*g)/2/g
print('Máxima reação em cada eixo: {0:5.2f} kgf'.format(R))
Máxima reação em cada eixo: 149.98 kgf