Universidade Federal do Rio Grande do Sul (UFRGS)
Programa de Pós-Graduação em Engenharia Civil (PPGEC)
PEC00025: Introduction to Vibration Theory¶
Test P2 (2021/1): multiple d.o.f. and continuous systems¶
NAME:
CARD:
Instruções¶
- Entregar a resolução da prova em arquivo único, com no máximo 10Mb, até às 12h de amanhã, 01 de junho de 2021.
- Recomenda-se verificar atentamente se todas as folhas da resolução foram incluídas no arquivo gerado, pois não serão aceitas entregas posteriores.
- Na primeira folha do arquivo deve constar claramente o NOME e o cartão de MATRÍCULA.
- A consulta ao material de estudo e o uso do computador para cálculos são LIVRES.
- A prova deve ser realizada INDIVIDUALMENTE, sem recorrer ao auxílio de colegas ou outras pessoas! Caso se verifique o descumprimento desta regra, todos os envolvidos na fraude terão a nota da prova zerada.
# Importing Python modules required for this notebook
# (this cell must be executed with "shift+enter" before any other Python cell)
import numpy as np
import scipy.linalg as sc
import matplotlib.pyplot as plt
from MRPy import *
Questão 1¶

Dados do problema:
H = 3. # altura de cada pavimento (m)
M = 10000. # massa de cada pavimento (kg)
f1 = 1. # frequência fundamental (Hz)
zt = 0.01 # amortecimento modal (adim., mesma nos dois modos)
g = 9.81 # aceleração da gravidade (m/s^2)
Função para cálculo dos modos de vibração:
def vibration_modes(K, M):
# 1. Uses scipy to solve the standard eigenvalue problem
w2, Phi = sc.eig(K, M)
# 2. Ensure ascending order of eigenvalues
iw = w2.argsort()
w2 = w2[iw]
Phi = Phi[:,iw]
# 3. Eigenvalues to vibration frequencies
wk = np.sqrt(np.real(w2))
fk = wk/2/np.pi
# 4. Mass matrix normalization
Mk = np.diag(np.dot(Phi.T, np.dot(M, Phi)))
for k in range(len(wk)):
Phi[:,k] = Phi[:,k]/np.sqrt(Mk[k])
# 5. Return results
return fk, wk, Phi
Monta matrizes e calcula modos:
K = 1.00 # rigidez de cada coluna (incógnita)
KG = K*np.array([[2, -2], [-2, 4]]) # rigidez global
MG = M*np.array([[1, 0], [ 0, 1]]) # massa global
fk, wk, Phi = vibration_modes(KG, MG)
K = (f1/fk[0])**2 # determina a rigidez correta
fk = fk*np.sqrt(K) # calcula todas as frequências
wk = fk*2*np.pi # em rad/s
print('Rigidez individual de cada barra: {0:6.1f}kN/m.'.format(K/1000))
print('Frequência no primeiro modo: {0:6.2f}Hz.'.format(fk[0]))
print('Frequência no segundo modo: {0:6.2f}Hz.'.format(fk[1]))
#print(wk)
Rigidez individual de cada barra: 516.8kN/m. Frequência no primeiro modo: 1.00Hz. Frequência no segundo modo: 2.62Hz.
Visualiza modos:
plt.figure(1, figsize=(12,8))
x = H*np.arange(3)
for k in range(2):
qk = np.zeros(3)
qk[1:] = Phi[::-1,k]
qk /= np.max(np.abs(qk)) # adjust scale for unity amplitude
plt.subplot(1,2,k+1)
plt.plot(qk, x, 'bo')
plt.plot(qk, x)
plt.xlim(-1.5, 1.5); plt.ylabel(str(k+1));
plt.ylim( 0.0, 7.0);
plt.title('fk = {0:4.2f}Hz'.format(fk[k]));
plt.grid(True)
Questão 2¶

A excitação tem mesma amplitude nas frequências de 0.5 e 3Hz. Para usar as amplificações dinâmicas, vamos admitir que o pico das respostas modais poderão estar em fase.
FG = 0.1*g*np.diag(MG).reshape(2,1) # amplitude das forças nos pavimentos
Fk = np.matmul(Phi.T, FG) # amplitude das forças modais
Mk = np.diag(np.dot(Phi.T, np.dot(MG, Phi))) # massas modais
Kk = wk*wk*Mk # rigidezes modais
uk = np.empty(2) # aloca memória para respostas modais
for k, fn in enumerate(fk):
bt = [0.5, 3.0]/fn # frequências componentes da excitação
AD = np.sqrt(1/((1 - bt**2)**2 + (2*zt*bt)**2)) # respectivas amplificações dinâmicas
uk[k] = (Fk[k]/Kk[k])*np.sum(AD) # pico da resposta modal amplificada
u = np.matmul(Phi,uk)
print('Máximo deslocamento no pavimento superior: {0:6.4f}m.'.format(u[0]))
Máximo deslocamento no pavimento superior: 0.0398m.
O mesmo cálculo agora por simulação, integrando por Fourier através do módulo MRPy:
Td = 32.
N = 1024
t = np.linspace(0, Td, N) # domínio do tempo
F = FG*(np.sin(np.pi*t) + np.sin(6*np.pi*t)) # força dinâmica
Calcula forças modais e resolve equações de equilíbrio desacopladas:
Fk = MRPy(np.matmul(Phi.T, F), Td=Td) # cria objeto MRPy
for k in range(2):
Fk[k,:] /= Mk[k] # prepara para solução
uk = Fk.sdof_Fourier(fk, zt) # calcula respostas modais
u = np.matmul(Phi,uk) # deslocamento nos pavimentos
print('Máximo deslocamento no pavimento superior: {0:6.4f}m.'.format(u[0,:].max()))
u.plot_time(1, figsize=(10,5));
Máximo deslocamento no pavimento superior: 0.0388m.
A diferença dos dois resultados se deve a que o pico das respostas modais não está perfeitamente em fase. Portanto a solução numérica, que é a mais precisa, apresenta amplitude ligeiramente menor.
Questão 3¶
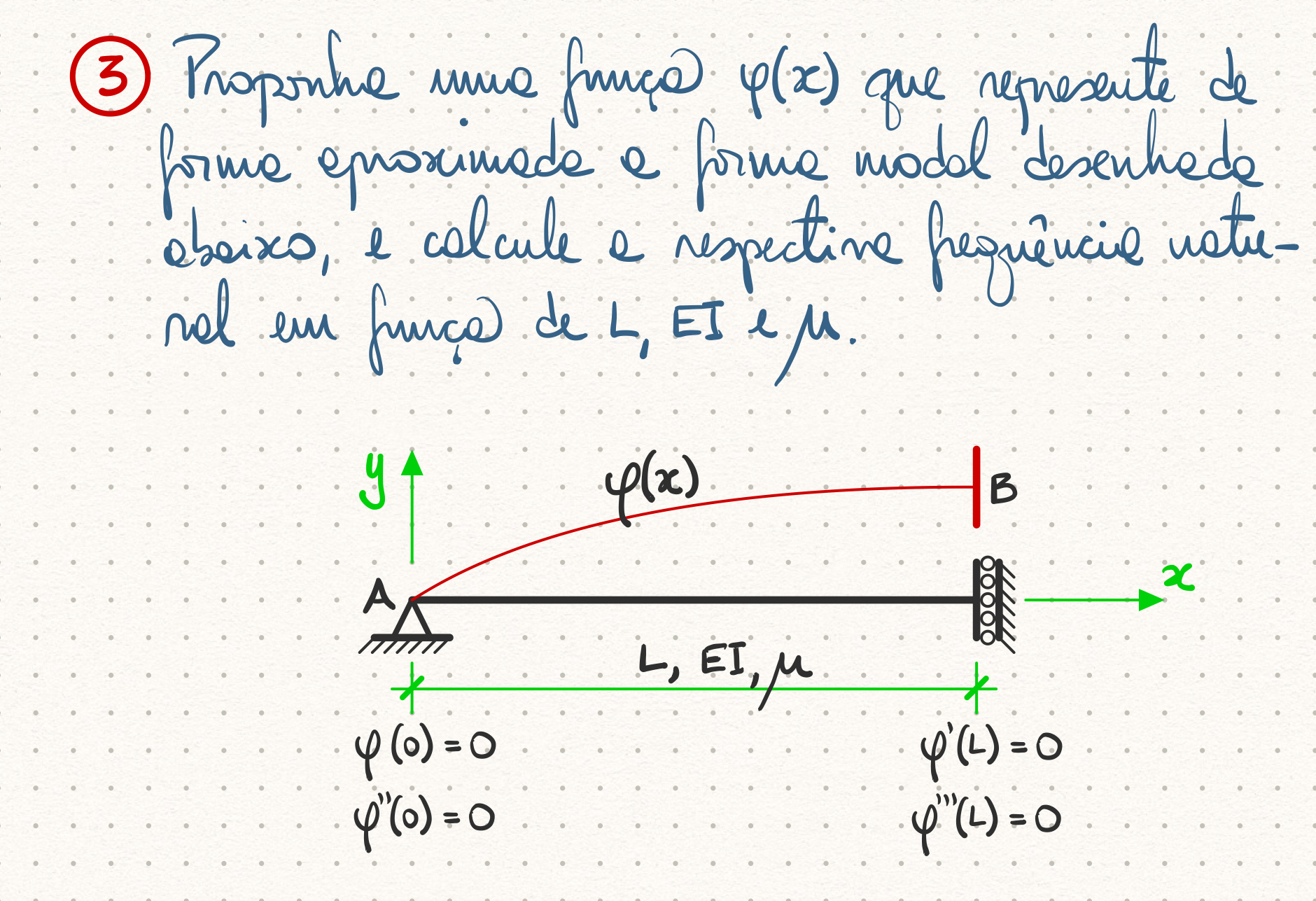
Primeiro vamos calcular a resposta exata, aplicando as condições de contorno na solução geral:
$$ \varphi(x) = C_1 \left(\cos px + \cosh px \right) + C_2 \left(\cos px - \cosh px \right) + C_3 \left(\sin px + \sinh px \right) + C_4 \left(\sin px - \sinh px \right) $$onde:
$$ p^4 = \left(\frac{\mu}{EI}\right) \omega^2 $$As condições de contorno são:
\begin{align*} \varphi(0) &= 0 \\ \varphi^{\prime\prime}(0) &= 0 \\ \varphi^{\prime}(L) &= 0 \\ \varphi^{\prime\prime\prime}(L) &= 0 \end{align*}Aplicando essas condições na solução geral temos, para $x = 0$:
\begin{align*} \varphi(0) &= C_1 \left( 1 + 1 \right) + C_2 \left( 1 - 1 \right) + C_3 \left( 0 + 0 \right) + C_4 \left( 0 - 0 \right) = 0 \\ \varphi^{\prime\prime}(0) &= C_1 \left(-1 + 1 \right) + C_2 \left(-1 - 1 \right) + C_3 \left(-0 + 0 \right) + C_4 \left(-0 - 0 \right) = 0 \end{align*}Portanto $C_1 = 0$ e $C_2 = 0$. Por outro lado, para $x = L$:
\begin{align*} \varphi^\prime(L) &= C_3 \left( \cos pL + \cosh pL \right) + C_4 \left( \cos pL - \cosh pL \right) = 0 \\ \varphi^{\prime\prime\prime}(L) &= C_3 \left(-\cos pL + \cosh pL \right) + C_4 \left(-\cos pL - \cosh pL \right) = 0 \end{align*}Colocando as equações acima em forma matricial temos:
$$ \left[ \begin{array}{cc} \left( \cos pL + \cosh pL \right) & \left( \cos pL - \cosh pL \right) \\ \left(-\cos pL + \cosh pL \right) & \left(-\cos pL - \cosh pL \right) \end{array} \right] \left[ \begin{array}{c} C_3 \\ C_4 \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right] $$Fazendo o determinante da matrix de coeficientes igual a zero temos as frequência naturais. Estas frequências podem ser calculadas numericamente, como mostrado abaixo.
def char_eq(x):
x = x[0]
A = np.array([[ np.cos(x)+np.cosh(x), np.cos(x)-np.cosh(x)],
[-np.cos(x)+np.cosh(x), -np.cos(x)-np.cosh(x)]])
return np.linalg.det(A)
#-----------------------------------------------------------------------
from scipy.optimize import fsolve
p = fsolve(char_eq, 1.0)
print('Cantilever beam frequency parameter is {0:8.6f}...'.format(p[0]))
Cantilever beam frequency parameter is 1.570796...
Ou seja, o parâmetro de frequência parece ser $\pi/2$ e a frequência fundamental resulta:
$$ \omega_1 = \left(\frac{\pi}{2L} \right)^2 \sqrt{\frac{EI}{\mu}} $$que coerentemente corresponde à frequência fundamental de uma viga bi-apoiada com vão $2L$. Isso está correto já que a condição de apoio da direita equivale a uma condição de simetria para uma viga com o dobro do vão!
Agora vamos refazer o cálculo propondo a seguinte função aproximada para a forma modal:
$$ \varphi(x) = \frac{1}{L^2}\left( 2Lx - x^2 \right) $$ou seja, uma parábola que apresenta derivada nula para $x = L$, e portanto respeita algumas condições de contorno. A escala desta forma modal é intencionalmente escolhida como sendo unitária. As derivadas dessa forma modal aproximada são:
\begin{align*} \varphi^{\prime}(x) &= (2L - 2x)\,/L^2 \\ \varphi^{\prime\prime}(x) &= -2\,/L^2 \end{align*}Observa-se que a função proposta não cumpre a condição de momento nulo na extremidade da esquerda, mas vamos em frente. A correspondente energia cinética de referência é:
$$ T_{\rm ref} = \frac{1}{2} \int_0^L {\mu \varphi ^2(x) \, dx} = \frac{4}{15} \, \mu L $$enquanto a energia potencial elástica resulta:
$$ V = \frac{1}{2} \int_0^L {EI \left[ \varphi^{\prime\prime}(x) \right] ^2 \, dx} = \frac{2EI}{L^3} $$Portanto o quociente de Rayleigh resulta:
$$ \omega_1 = \sqrt{\frac{V}{T_{\rm ref}}} = \sqrt{\frac{2EI \cdot 15}{4\mu L^4}} = \left(\frac{120^{1/4}}{2L} \right)^2 \sqrt{\frac{EI}{\mu}} $$onde $120^{1/4} \approx 3.31$ e portanto esse valor apresenta um erro de aproximadamente 5.4%, esperado em relação ao valor correto, $\pi$, e um erro de aproximadamente 11% em relação à frequência correta. Observe que o quociente de Rayleigh sempre fornece frequência igual ou maior que a exata.
Questão 4¶

Dados do problema:
L = 6. # comprimento da viga (m)
m = 80. # massa da pessoa (kg)
mu = 200. # massa por unidade de comprimento (kg/m)
EI = 36.e6 # rigidez à flexão (Nm^2)
Vamos considerar a resposta apenas no primeiro modo. A dissipação de energia por amortecimento é desprezada e a energia total do sistema deve se manter constante e igual à a energia potencial gravitacional da pessoa no início da queda:
$$ E = mgh = 784.8{\rm J}$$Por questão de simplicidade, admite-se que a viga já está deformada por peso próprio quando se determina a altura de queda da pessoa. Também vamos considerar que o choque é perfeitamente inelástico, ou seja, a viga e a pessoa seguem unidos após o contato.
Observe que forma modal proposta é normalizada pela unidade, de modo que ela tem valor unitário na extremidade da direita, $\varphi(L) = 1$. Desta forma, deslocamento vertical e deslocamento modal tem mesmo valor numérico no ponto B.
A energia cinética total do sistema após o choque é calculada como:
$$ T = \frac{1}{2} \int_0^L {\mu \left[ v_0 \varphi(x) \right]^2 \, dx} + \frac{1}{2} m\left[ v_0 \varphi(L) \right] ^2 = 360v_0^2$$onde $v_0$ é a velocidade inicial da extremidade direita da viga logo após o choque, que é numericamente igual à velocidade inicial no espaço modal. Igualando-se as energias, $E = T$, chega-se a:
$$ v_0 = \sqrt{\frac{784.8}{360}} \approx 1.48{\rm m/s}$$A frequência natural no primeiro modo precisa ser re-calculada, pois agora a viga tem também a massa da pessoa incorporada na extremidade direita. A nova energia cinética de referência é:
$$ T_{\rm ref} = \frac{1}{2} \int_0^L {\mu \varphi^2(x) \, dx} + \frac{1}{2} m \varphi^2(L) = 360 $$A energia potencial elástica, $V$, permanece a mesma e, portanto, a frequência natural resulta menor:
$$ \omega_{\rm n} = \sqrt{\frac{V}{T_{\rm ref}}} = \sqrt{\frac{2\cdot 36\times 10^6}{360 \cdot 6^3}} \approx 30.42{\rm rad/s} $$Sem a massa da pessoa incorporada, a frequência natural calculada na seção anterior seria de $32.27{\rm rad/s}$.
A amplitude total do delocamento modal é a soma da amplitude devida à velocidade inicial com o deslocamento devido à carga impulsiva. Dada a escala unitária da forma modal, a força modal tem o mesmo módulo da força aplicada na extremidade da direita. O formato retangular da carga impulsiva (choque inelástico) implica que o fator de amplificação dinâmica, $A$, da resposta estática, $u_{B, \rm est}$, é igual a 2.
$$ u_{B, \rm max} = \frac{v_0}{\omega_{\rm n}} + A \, u_{B, \rm est} $$Para calcular a resposta estática é necessário conhecer a massa modal:
$$ M = \int_0^L {\mu \varphi^2(x) \, dx} + m \varphi^2(L) = 720{\rm kg}$$Lembrando que a rigidez modal é dada por $K = \omega^2_{\rm n} M$, a resposta estática é calculada como:
$$ u_{B, \rm est} = \frac{mg \varphi(L)}{K} = \frac{80 \cdot 9.81 \cdot 1}{30.42^2 \cdot 720} \approx 1.18{\rm mm}$$Substituindo valores:
$$ u_{B, \rm max} = \frac{1.48}{30.42} + 2 \cdot 0.00118 \approx 5.1{\rm cm}$$