Python数据科学分享——2.数据处理¶

Python数据处理历史悠久，除了基础的Numpy、Scipy、pandas构建繁荣生态，还有谷歌推出的tensorflow、jax高性能工具

toc: true
badges: true
comments: true
categories: [jupyter,Python,Data Science]

In [1]:

%load_ext autoreload
%autoreload 2

import matplotlib.pyplot as plt
import seaborn

seaborn.set()
plt.rcParams["font.sans-serif"] = ["SimHei"]
import numpy as np
import pandas as pd
from scipy import sparse
from tqdm.notebook import tqdm

python数值计算历史

首发年份	名称	场景
1991	Python	编程语言
2001	ipython	增强shell
2001	SciPy	算法库
2006	Numpy	数组运算
2007	Cython	AOT静态编译
2008	Pandas	标签数组运算
2010	scikit-learn	机器学习
2012	ipython notebook	计算环境
2012	anaconda	管理工具
2012	Numba	llvm实现JIT编译器
2012	pyspark	集群运算
2015	jupyter	多语言支持
2015	TensorFlow	深度学习
2018	jax	Numpy+autogrd+JIT+GPU+TPU

With great power comes great complexity（越强大越复杂）

Numpy¶

神经网络示例¶

背景¶

In [1]:

from IPython.display import Video

# https://github.com/Sentdex/NNfSiX

# Video("2.data-elt/cat_neural_network.mp4", embed=True)

x1	x2	x3	Y
0	0	1	0
0	1	1	1
1	0	1	1
1	1	1	0

In [3]:

X = np.array([[0, 0, 1], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
y = np.array([[0], [1], [1], [0]])

网络图¶

数学描述¶

公式1 $$ \hat y = \sigma(W_2\sigma(W_1x+ b_1) + b_2) $$

公式2（sigmoid） $$ \sigma = \frac {1} {1 + e^{-x}} $$

公式3（sigmoid导数） $$ \sigma' = \sigma(x) \times (1 - \sigma(x)) $$

反向传播¶

公式4 $$ Loss(Sum\ of\ Squares\ Error) = \sum_{i=1}^n(y-\hat y)^2 $$

numpy实现¶

In [4]:

def σ(x):
    return 1 / (1 + np.exp(-x))


def σ_dvt(x):
    return σ(x) * (1 - σ(x))


class NeuralNetwork(object):
    def __init__(self, x, y):
        self.x = x
        self.y = y
        self.w1 = np.random.rand(self.x.shape[1], 4)
        self.w2 = np.random.rand(4, 1)
        self.yhat = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = σ(self.x @ self.w1)
        self.yhat = σ(self.layer1 @ self.w2)

    def backprop(self):
        gd = 2 * (self.y - self.yhat) * σ_dvt(self.yhat)
        d_w2 = self.layer1.T @ gd
        d_w1 = self.x.T @ (gd @ (self.w2.T) * σ_dvt(self.layer1))

        self.w1 += d_w1
        self.w2 += d_w2

In [5]:

nn = NeuralNetwork(X, y)

train = []
for i in tqdm(range(10000)):
    nn.feedforward()
    nn.backprop()
    loss = sum((_[0] - _[1])[0] ** 2 for _ in zip(nn.y, nn.yhat))
    train.append(loss)

print(nn.yhat)

HBox(children=(FloatProgress(value=0.0, max=10000.0), HTML(value='')))

[[0.00644673]
 [0.9909493 ]
 [0.99080728]
 [0.00803459]]

In [11]:

def show_plot(x, y):
    plt.figure(figsize=(15, 5))
    plt.plot(
        x,
        y,
        linewidth=3,
        linestyle=":",
        color="blue",
        label="Sum of Squares Error",
    )
    plt.xlabel("训练次数")
    plt.ylabel("训练损失")
    plt.title("训练损失随次数增加而递减")
    plt.legend(loc="upper right")
    plt.show()

In [12]:

show_plot(range(len(train)), train)

In [13]:

show_plot(range(4000, len(train)), train[4000:])

数据结构¶

NumPy在C语言的基础上开发ndarray对象，其数据类型也是在C语言基础上进行扩充。

CPython的整型对象是一个PyObject_HEAD是C语言结构体，包含引用计数、类型编码和数据大小等信息，相比C语言的整型增加了很多开销，Numpy进行了优化。

数组初始化¶

In [14]:

# 创建一个长度为10的数组，数组的值都是0
np.zeros(10, dtype=int)

Out[14]:

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])

In [15]:

# 创建一个3x5的浮点型数组，数组的值都是1
np.ones((3, 5), dtype=float)

Out[15]:

array([[1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1.]])

In [16]:

# 创建一个3x5的浮点型数组，数组的值都是3.14
np.full((3, 5), 3.14)

Out[16]:

array([[3.14, 3.14, 3.14, 3.14, 3.14],
       [3.14, 3.14, 3.14, 3.14, 3.14],
       [3.14, 3.14, 3.14, 3.14, 3.14]])

In [17]:

# 创建一个线性序列数组，从0开始，到20结束，步长为2（它和内置的range()函数类似）
np.arange(0, 20, 2)

Out[17]:

array([ 0,  2,  4,  6,  8, 10, 12, 14, 16, 18])

In [18]:

# 创建一个5个元素的数组，这5个数均匀地分配到0~1区间
np.linspace(0, 1, 5)

Out[18]:

array([0.  , 0.25, 0.5 , 0.75, 1.  ])

In [19]:

# NumPy的随机数生成器设置一组种子值，以确保每次程序执行时都可以生成同样的随机数组：
np.random.seed(1024)

# 创建一个3x3的、0~1之间均匀分布的随机数组成的数组
np.random.random((3, 3))

Out[19]:

array([[0.64769123, 0.99691358, 0.51880326],
       [0.65811273, 0.59906347, 0.75306733],
       [0.13624713, 0.00411712, 0.14950888]])

In [20]:

# 创建一个3x3的、均值为0、标准差为1的正态分布的随机数数组
np.random.normal(0, 1, (3, 3))

Out[20]:

array([[ 0.7729004 ,  1.64294992, -0.12721717],
       [ 0.91598327,  0.52267255, -0.22634267],
       [ 1.41873344, -0.16232799,  0.53831355]])

In [21]:

# 创建一个3x3的、[0, 10)区间的随机整型数组
np.random.randint(0, 10, (3, 3))

Out[21]:

array([[6, 4, 4],
       [1, 0, 1],
       [8, 7, 0]])

In [22]:

# 创建一个3x3的单位矩阵
np.eye(3)

Out[22]:

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

In [23]:

# 创建一个由3个整型数组成的未初始化的数组，数组的值是内存空间中的任意值
np.empty(3)

Out[23]:

array([1., 1., 1.])

属性：确定数组的大小、形状、存储大小、数据类型
读写：数组保存与加载文件
数学运算：加减乘除、指数与平方根、三角函数、聚合比较等基本运算
复制与排序：数组深浅copy、快速排序、归并排序和堆排序
索引：获取和设置数组各个元素的值
切分：在数组中获取或设置子数组
变形：改变给定数组的形状
连接和分裂：将多个数组合并为一个，或者将一个数组分裂成多个

通用函数(universal functions, ufunc)¶

NumPy实现一种静态类型、可编译程序接口（ufunc），实现向量化(vectorize)操作，避免for循环，提高效率，节约内存。

通用函数有两种存在形式：

一元通用函数（unary ufunc）对单个输入操作
二元通用函数（binary ufunc）对两个输入操作

数组的运算¶

NumPy通用函数的使用方式非常自然，因为它用到了Python原生的算术运算符(加、减、乘、除)、绝对值、三角函数、指数与对数、布尔/位运算符。

运算符	对应的通用函数	描述
`+`	`np.add`	加法运算（即`1 + 1 = 2`）
`-`	`np.subtract`	减法运算（即`3 - 2 = 1`）
`-`	`np.negative`	负数运算（即`-2`）
`*`	`np.multiply`	乘法运算（即`2 * 3 = 6`）
`/`	`np.divide`	除法运算（即`3 / 2 = 1.5`）
`//`	`np.floor_divide`	地板除法运算（floor division，即`3 // 2 = 1`）
`**`	`np.power`	指数运算（即`2 ** 3 = 8`）
`%`	`np.mod`	模/余数（即`9 % 4 = 1`）
	`np.abs`	绝对值

In [24]:

x = np.arange(4)
print("x     =", x)
print("x + 5 =", x + 5)
print("x - 5 =", x - 5)
print("x * 2 =", x * 2)
print("x / 2 =", x / 2)
print("x // 2 =", x // 2)  # 整除运算

x     = [0 1 2 3]
x + 5 = [5 6 7 8]
x - 5 = [-5 -4 -3 -2]
x * 2 = [0 2 4 6]
x / 2 = [0.  0.5 1.  1.5]
x // 2 = [0 0 1 1]

In [25]:

x = [1, 2, 3]
print("x     =", x)
print("e^x   =", np.exp(x))
print("2^x   =", np.exp2(x))
print("3^x   =", np.power(3, x))
print("x        =", x)
print("ln(x)    =", np.log(x))
print("log2(x)  =", np.log2(x))
print("log10(x) =", np.log10(x))

x     = [1, 2, 3]
e^x   = [ 2.71828183  7.3890561  20.08553692]
2^x   = [2. 4. 8.]
3^x   = [ 3  9 27]
x        = [1, 2, 3]
ln(x)    = [0.         0.69314718 1.09861229]
log2(x)  = [0.        1.        1.5849625]
log10(x) = [0.         0.30103    0.47712125]

特殊ufunc¶

scipy.special提供了大量统计学函数。例如，Γ函数和β函数

In [26]:

from scipy import special

x = [1, 5, 10]
print("gamma(x)     =", special.gamma(x))
print("ln|gamma(x)| =", special.gammaln(x))
print("beta(x, 2)   =", special.beta(x, 2))

gamma(x)     = [1.0000e+00 2.4000e+01 3.6288e+05]
ln|gamma(x)| = [ 0.          3.17805383 12.80182748]
beta(x, 2)   = [0.5        0.03333333 0.00909091]

高级特性¶

累计¶

二元通用函数的reduce方法可以对给定元素和操作重复执行，直至得到一个汇总结果。accumulate方法实现截至每一个元素的累积结果

例如，对add通用函数调用reduce方法会返回数组中所有元素的和：

In [27]:

x = np.arange(1, 6)
np.add.reduce(x)

Out[27]:

同样，对multiply通用函数调用reduce方法会返回数组中所有元素的乘积：

In [28]:

np.multiply.reduce(x)   

Out[28]:

In [29]:

np.add.accumulate(x) 

Out[29]:

array([ 1,  3,  6, 10, 15])

In [30]:

np.multiply.accumulate(x)

Out[30]:

array([  1,   2,   6,  24, 120])

NumPy提供了专用的函数（np.sum、np.prod、np.cumsum、np.cumprod ），它们也可以实现reduce的功能

外积¶

任何通用函数都可以用outer方法获得两个不同输入数组所有元素对的函数运算结果。用一行代码实现一个99乘法表：

In [31]:

x = np.arange(1, 10)
np.multiply.outer(x, x)

Out[31]:

array([[ 1,  2,  3,  4,  5,  6,  7,  8,  9],
       [ 2,  4,  6,  8, 10, 12, 14, 16, 18],
       [ 3,  6,  9, 12, 15, 18, 21, 24, 27],
       [ 4,  8, 12, 16, 20, 24, 28, 32, 36],
       [ 5, 10, 15, 20, 25, 30, 35, 40, 45],
       [ 6, 12, 18, 24, 30, 36, 42, 48, 54],
       [ 7, 14, 21, 28, 35, 42, 49, 56, 63],
       [ 8, 16, 24, 32, 40, 48, 56, 64, 72],
       [ 9, 18, 27, 36, 45, 54, 63, 72, 81]])

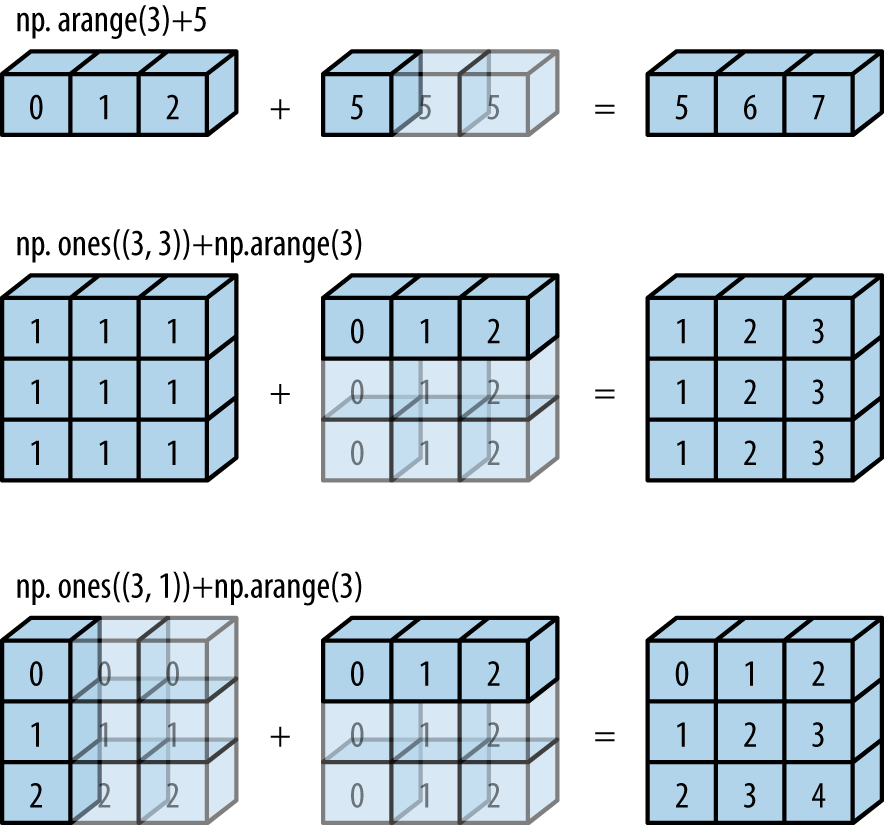
广播(Broadcasting)¶

NumPy也可以通过广播实现向量化操作。广播可以用于不同大小数组的二元通用函数（加、减、乘等）的一组规则:

规则1：如果两个数组的维度数不相同，那么小维度数组的形状将会在最左边补1。
规则2：如果两个数组的形状在任何一个维度上都不匹配，那么数组的形状会沿着维度为1的维度扩展以匹配另外一个数组的形状。
规则3：如果两个数组的形状在任何一个维度上都不匹配并且没有任何一个维度等于1，那么会引发异常。

In [32]:

a = np.arange(3)
a + 5

Out[32]:

array([5, 6, 7])

In [33]:

np.ones((3, 3)) + a

Out[33]:

array([[1., 2., 3.],
       [1., 2., 3.],
       [1., 2., 3.]])

根据规则1，数组a的维度数更小，所以在其左边补1：

b.shape -> (3, 3)

a.shape -> (1, 3)

根据规则2，第一个维度不匹配，因此扩展这个维度以匹配数组：

b.shape -> (3, 3)

a.shape -> (3, 3)

现在两个数组的形状匹配了，可以看到它们的最终形状都为(3, 3)：

In [34]:

b = np.arange(3)[:, np.newaxis] 

b + a

Out[34]:

array([[0, 1, 2],
       [1, 2, 3],
       [2, 3, 4]])

根据规则1，数组a的维度数更小，所以在其左边补1：

b.shape -> (3, 1)

a.shape -> (1, 3)

根据规则2，两个维度都不匹配，因此扩展这个维度以匹配数组：

b.shape -> (3, 3)

a.shape -> (3, 3)

现在两个数组的形状匹配了，可以看到它们的最终形状都为(3, 3)：

Scipy稀疏矩阵¶

地球70多亿人的社交网络中，大部分人直接认识的人数不超过10000，因此这个矩阵中，大部分的值都是0（稀疏）

In [35]:

SN = np.random.poisson(0.2, (10, 10)) * np.random.randint(0, 10, (10, 10))
SN

Out[35]:

array([[ 8,  0,  0,  0,  9,  0,  0,  0,  0,  3],
       [ 0,  0,  9,  0,  7,  0,  0,  0,  0,  4],
       [ 0,  0,  0,  0,  0,  0,  0,  0,  8,  0],
       [ 0,  0,  0,  9,  0,  0,  0,  4,  0,  0],
       [ 0,  5,  0,  0,  0,  7,  0,  0,  0,  0],
       [ 0,  8,  8,  1,  0,  1,  4,  0,  0,  0],
       [ 0, 18,  0,  0,  0,  0,  0,  0,  0,  4],
       [ 0,  0,  4,  0,  0,  0,  5,  0,  0,  0],
       [ 0,  0,  0,  0,  5,  0,  0,  0,  0,  0],
       [ 0,  0,  0,  9,  0,  0,  4,  0,  0,  0]])

In [36]:

rows, cols = np.nonzero(SN)
vals = SN[rows, cols]
rows, cols, vals

Out[36]:

(array([0, 0, 0, 1, 1, 1, 2, 3, 3, 4, 4, 5, 5, 5, 5, 5, 6, 6, 7, 7, 8, 9,
        9]),
 array([0, 4, 9, 2, 4, 9, 8, 3, 7, 1, 5, 1, 2, 3, 5, 6, 1, 9, 2, 6, 4, 3,
        6]),
 array([ 8,  9,  3,  9,  7,  4,  8,  9,  4,  5,  7,  8,  8,  1,  1,  4, 18,
         4,  4,  5,  5,  9,  4]))

稀疏矩阵初始化¶

In [37]:

X = sparse.coo_matrix(SN)
X

Out[37]:

<10x10 sparse matrix of type '<class 'numpy.int64'>'
	with 23 stored elements in COOrdinate format>

In [38]:

print(X)

  (0, 0)	8
  (0, 4)	9
  (0, 9)	3
  (1, 2)	9
  (1, 4)	7
  (1, 9)	4
  (2, 8)	8
  (3, 3)	9
  (3, 7)	4
  (4, 1)	5
  (4, 5)	7
  (5, 1)	8
  (5, 2)	8
  (5, 3)	1
  (5, 5)	1
  (5, 6)	4
  (6, 1)	18
  (6, 9)	4
  (7, 2)	4
  (7, 6)	5
  (8, 4)	5
  (9, 3)	9
  (9, 6)	4

按坐标创建稀疏矩阵¶

In [39]:

X2 = sparse.coo_matrix((vals, (rows, cols)))

In [40]:

X2.todense()

Out[40]:

matrix([[ 8,  0,  0,  0,  9,  0,  0,  0,  0,  3],
        [ 0,  0,  9,  0,  7,  0,  0,  0,  0,  4],
        [ 0,  0,  0,  0,  0,  0,  0,  0,  8,  0],
        [ 0,  0,  0,  9,  0,  0,  0,  4,  0,  0],
        [ 0,  5,  0,  0,  0,  7,  0,  0,  0,  0],
        [ 0,  8,  8,  1,  0,  1,  4,  0,  0,  0],
        [ 0, 18,  0,  0,  0,  0,  0,  0,  0,  4],
        [ 0,  0,  4,  0,  0,  0,  5,  0,  0,  0],
        [ 0,  0,  0,  0,  5,  0,  0,  0,  0,  0],
        [ 0,  0,  0,  9,  0,  0,  4,  0,  0,  0]])

数据压缩¶

将稀疏矩阵保存为 CSR(Compressed Sparse Row)/CSC(Compressed Sparse Column) 格式

In [41]:

np.vstack([rows, cols])

Out[41]:

array([[0, 0, 0, 1, 1, 1, 2, 3, 3, 4, 4, 5, 5, 5, 5, 5, 6, 6, 7, 7, 8, 9,
        9],
       [0, 4, 9, 2, 4, 9, 8, 3, 7, 1, 5, 1, 2, 3, 5, 6, 1, 9, 2, 6, 4, 3,
        6]])

In [42]:

indptr = np.r_[np.searchsorted(rows, np.unique(rows)), len(rows)]
indptr

Out[42]:

array([ 0,  3,  6,  7,  9, 11, 16, 18, 20, 21, 23])

In [43]:

X3 = sparse.csr_matrix((vals, cols, indptr))
X3

Out[43]:

<10x10 sparse matrix of type '<class 'numpy.int64'>'
	with 23 stored elements in Compressed Sparse Row format>

In [44]:

print(X3)

  (0, 0)	8
  (0, 4)	9
  (0, 9)	3
  (1, 2)	9
  (1, 4)	7
  (1, 9)	4
  (2, 8)	8
  (3, 3)	9
  (3, 7)	4
  (4, 1)	5
  (4, 5)	7
  (5, 1)	8
  (5, 2)	8
  (5, 3)	1
  (5, 5)	1
  (5, 6)	4
  (6, 1)	18
  (6, 9)	4
  (7, 2)	4
  (7, 6)	5
  (8, 4)	5
  (9, 3)	9
  (9, 6)	4

In [45]:

X3.todense()

Out[45]:

matrix([[ 8,  0,  0,  0,  9,  0,  0,  0,  0,  3],
        [ 0,  0,  9,  0,  7,  0,  0,  0,  0,  4],
        [ 0,  0,  0,  0,  0,  0,  0,  0,  8,  0],
        [ 0,  0,  0,  9,  0,  0,  0,  4,  0,  0],
        [ 0,  5,  0,  0,  0,  7,  0,  0,  0,  0],
        [ 0,  8,  8,  1,  0,  1,  4,  0,  0,  0],
        [ 0, 18,  0,  0,  0,  0,  0,  0,  0,  4],
        [ 0,  0,  4,  0,  0,  0,  5,  0,  0,  0],
        [ 0,  0,  0,  0,  5,  0,  0,  0,  0,  0],
        [ 0,  0,  0,  9,  0,  0,  4,  0,  0,  0]])

In [46]:

X4 = X2.tocsr()

X4

Out[46]:

<10x10 sparse matrix of type '<class 'numpy.longlong'>'
	with 23 stored elements in Compressed Sparse Row format>

In [47]:

print(X4)

  (0, 0)	8
  (0, 4)	9
  (0, 9)	3
  (1, 2)	9
  (1, 4)	7
  (1, 9)	4
  (2, 8)	8
  (3, 3)	9
  (3, 7)	4
  (4, 1)	5
  (4, 5)	7
  (5, 1)	8
  (5, 2)	8
  (5, 3)	1
  (5, 5)	1
  (5, 6)	4
  (6, 1)	18
  (6, 9)	4
  (7, 2)	4
  (7, 6)	5
  (8, 4)	5
  (9, 3)	9
  (9, 6)	4

In [48]:

X5 = X2.tocsc()

X5

Out[48]:

<10x10 sparse matrix of type '<class 'numpy.longlong'>'
	with 23 stored elements in Compressed Sparse Column format>

In [49]:

print(X5)

  (0, 0)	8
  (4, 1)	5
  (5, 1)	8
  (6, 1)	18
  (1, 2)	9
  (5, 2)	8
  (7, 2)	4
  (3, 3)	9
  (5, 3)	1
  (9, 3)	9
  (0, 4)	9
  (1, 4)	7
  (8, 4)	5
  (4, 5)	7
  (5, 5)	1
  (5, 6)	4
  (7, 6)	5
  (9, 6)	4
  (3, 7)	4
  (2, 8)	8
  (0, 9)	3
  (1, 9)	4
  (6, 9)	4

COO合计转换¶

coo_matrix会默认将重复元素求和，适合构造多分类模型的混淆矩阵

In [50]:

rows = np.repeat([0, 1], 4)
cols = np.repeat([0, 1], 4)
vals = np.arange(8)

In [51]:

rows, cols, vals

Out[51]:

(array([0, 0, 0, 0, 1, 1, 1, 1]),
 array([0, 0, 0, 0, 1, 1, 1, 1]),
 array([0, 1, 2, 3, 4, 5, 6, 7]))

In [52]:

X6 = sparse.coo_matrix((vals, (rows, cols)))

X6.todense()

Out[52]:

matrix([[ 6,  0],
        [ 0, 22]])

2X2混淆矩阵¶

In [53]:

y_true = np.random.randint(0, 2, 100)
y_pred = np.random.randint(0, 2, 100)
vals = np.ones(100).astype("int")

y_true, y_pred

Out[53]:

(array([0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0,
        1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1,
        1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1,
        1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1,
        1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1]),
 array([0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1,
        1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0,
        0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1,
        0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0,
        0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0]))

In [54]:

vals.shape, y_true.shape, y_pred.shape

Out[54]:

((100,), (100,), (100,))

In [55]:

X7 = sparse.coo_matrix((vals, (y_true, y_pred)))

X7.todense()

Out[55]:

matrix([[21, 23],
        [30, 26]])

In [56]:

from sklearn.metrics import confusion_matrix

confusion_matrix(y_true, y_pred)

Out[56]:

array([[21, 23],
       [30, 26]])

In [57]:

y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
confusion_matrix(y_true, y_pred, labels=["ant", "bird", "cat"])

Out[57]:

array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

Pandas ¶

Series 与 Dataframe¶

Series：键值对形成的二序序列，有标签的numpy一维数组
Dataframe：行列值三元序列（类似excel表），有标签的numpy二维数组
Input/output
General functions
Pandas arrays
Index objects
Date offsets
Window
GroupBy
Resampling
Style
Plotting
General utility functions
Extensions

向量化字符串操作 ¶

Pandas提供了一系列向量化字符串操作（vectorized string operation），极大地提高了字符串清洗效率。Pandas为包含字符串的Series和Index对象提供了str属性，既可以处理字符串，又可以处理缺失值。

字符串方法¶

所有Python内置的字符串方法都被复制到Pandas的向量化字符串方法中：

这些方法的返回值并不完全相同，例如lower()方法返回字符串，len()方法返回数值，startswith('T')返回布尔值，split()方法返回列表

In [59]:

monte = pd.Series(
    (
        "Gerald R. Ford",
        "James Carter",
        "Ronald Reagan",
        "George H. W. Bush",
        "William J. Clinton",
        "George W. Bush",
        "Barack Obama",
        "Donald J. Trump",
    )
)

In [60]:

monte.str.len()

Out[60]:

0    14
1    12
2    13
3    17
4    18
5    14
6    12
7    15
dtype: int64

正则表达式¶

有一些方法支持正则表达式处理字符串。下面是Pandas根据Python标准库的re模块函数实现的API：

方法	描述
`match()`	对每个元素调用`re.match()`，返回布尔类型值
`extract()`	对每个元素调用`re.match()`，返回匹配的字符串组（`groups`）
`findall()`	对每个元素调用`re.findall()`
`replace()`	用正则模式替换字符串
`contains()`	对每个元素调用`re.search()`，返回布尔类型值
`count()`	计算符合正则模式的字符串的数量
`split()`	等价于`str.split()`，支持正则表达式
`rsplit()`	等价于`str.rsplit()`，支持正则表达式

In [61]:

monte.str.extract('([A-Za-z]+)')

Out[61]:

	0
0	Gerald
1	James
2	Ronald
3	George
4	William
5	George
6	Barack
7	Donald

找出所有开头和结尾都是辅音字母的名字——这可以用正则表达式中的开始符号（^）与结尾符号（$）来实现：

In [62]:

monte.str.findall(r'^[^AEIOU].*[^aeiou]$')

Out[62]:

0        [Gerald R. Ford]
1          [James Carter]
2         [Ronald Reagan]
3     [George H. W. Bush]
4    [William J. Clinton]
5        [George W. Bush]
6                      []
7       [Donald J. Trump]
dtype: object

其他字符串方法¶

还有其他一些方法可以实现更方便的操作

方法	描述
`get()`	获取元素索引位置上的值，索引从0开始
`slice()`	对元素进行切片取值
`slice_replace()`	对元素进行切片替换
`cat()`	连接字符串（此功能比较复杂，建议阅读文档）
`repeat()`	重复元素
`normalize()`	将字符串转换为Unicode规范形式
`pad()`	在字符串的左边、右边或两边增加空格
`wrap()`	将字符串按照指定的宽度换行
`join()`	用分隔符连接`Series`的每个元素
`get_dummies()`	按照分隔符提取每个元素的`dummy`变量，转换为独热（one-hot）编码的`DataFrame`

向量化字符串的取值与切片操作¶

get()与slice()操作可以从每个字符串数组中获取向量化元素。例如，我们可以通过str.slice(0, 3)获取每个字符串数组的前3个字符，df.str.slice(0, 3)=df.str[0:3]，df.str.get(i)=df.str[i]

In [63]:

monte.str[0:3]

Out[63]:

0    Ger
1    Jam
2    Ron
3    Geo
4    Wil
5    Geo
6    Bar
7    Don
dtype: object

get()与slice()操作还可以在split()操作之后使用。例如，要获取每个姓名的姓（last name），可以结合使用split()与get()：

In [64]:

monte.str.split().str.get(-1)

Out[64]:

0       Ford
1     Carter
2     Reagan
3       Bush
4    Clinton
5       Bush
6      Obama
7      Trump
dtype: object

指标变量¶

get_dummies()方法可以快速将指标变量分割成一个独热编码的DataFrame（每个元素都是0或1），如A=出生在美国、B=出生在英国、C=喜欢奶酪、D=喜欢午餐肉：

In [65]:

full_monte = pd.DataFrame(
    {
        "name": monte,
        "info": ["B|C|D", "B|D", "A|C", "B|D", "B|C", "A|C", "B|D", "B|C|D"],
    }
)
full_monte

Out[65]:

	name	info
0	Gerald R. Ford	B\|C\|D
1	James Carter	B\|D
2	Ronald Reagan	A\|C
3	George H. W. Bush	B\|D
4	William J. Clinton	B\|C
5	George W. Bush	A\|C
6	Barack Obama	B\|D
7	Donald J. Trump	B\|C\|D

In [66]:

full_monte['info'].str.get_dummies('|') 

Out[66]:

	A	B	C	D
0	0	1	1	1
1	0	1	0	1
2	1	0	1	0
3	0	1	0	1
4	0	1	1	0
5	1	0	1	0
6	0	1	0	1
7	0	1	1	1

处理时间序列¶

由于Pandas最初是为金融模型而创建的，因此日期时间数据处理功能非常强大

Pandas的日期与时间工具¶

Pandas所有关于日期与时间的处理方法全部都是通过Timestamp对象实现的，可以作为Series或DataFrame的索引DatetimeIndex。例如，可以用Pandas的方式演示前面介绍的日期与时间功能。我们可以灵活处理不同格式的日期与时间字符串，获取某一天是星期几：

In [67]:

date = pd.to_datetime("4th of May, 2020")
date

Out[67]:

Timestamp('2020-05-04 00:00:00')

In [68]:

date.strftime('%A')

Out[68]:

'Monday'

可以直接进行NumPy类型的向量化运算：

In [69]:

date + pd.to_timedelta(np.arange(12), 'D')

Out[69]:

DatetimeIndex(['2020-05-04', '2020-05-05', '2020-05-06', '2020-05-07',
               '2020-05-08', '2020-05-09', '2020-05-10', '2020-05-11',
               '2020-05-12', '2020-05-13', '2020-05-14', '2020-05-15'],
              dtype='datetime64[ns]', freq=None)

Pandas时间序列：用时间作索引¶

Pandas时间序列工具非常适合用来处理带时间戳的索引数据。

通过一个时间索引数据创建一个Series对象：

In [70]:

index = pd.DatetimeIndex(["2019-01-04", "2019-02-04", "2020-03-04", "2020-04-04"])
data = pd.Series([0, 1, 2, 3], index=index)
data

Out[70]:

2019-01-04    0
2019-02-04    1
2020-03-04    2
2020-04-04    3
dtype: int64

直接用日期进行切片取值：

In [71]:

data['2020-02-04':'2020-04-04']

Out[71]:

2020-03-04    2
2020-04-04    3
dtype: int64

直接通过年份切片获取该年的数据：

In [72]:

data['2020']
 

Out[72]:

2020-03-04    2
2020-04-04    3
dtype: int64

Pandas时间序列数据结构¶

本节将介绍Pandas用来处理时间序列的基础数据类型。

时间戳，Pandas提供了Timestamp类型。本质上是Python的原生datetime类型的替代品，但是在性能更好的numpy.datetime64类型的基础上创建。对应的索引数据结构是DatetimeIndex。
时间周期，Pandas提供了Period类型。这是利用numpy.datetime64类型将固定频率的时间间隔进行编码。对应的索引数据结构是PeriodIndex。
时间增量或持续时间，Pandas提供了Timedelta类型。Timedelta是一种代替Python原生datetime.timedelta类型的高性能数据结构，同样是基于numpy.timedelta64类型。对应的索引数据结构是TimedeltaIndex。

最基础的日期/时间对象是Timestamp和DatetimeIndex，对pd.to_datetime()传递一个日期会返回一个Timestamp类型，传递一个时间序列会返回一个DatetimeIndex类型：

In [73]:

from datetime import datetime

dates = pd.to_datetime(
    [datetime(2020, 7, 3), "4th of July, 2020", "2020-Jul-6", "07-07-2020", "20200708"]
)
dates

Out[73]:

DatetimeIndex(['2020-07-03', '2020-07-04', '2020-07-06', '2020-07-07',
               '2020-07-08'],
              dtype='datetime64[ns]', freq=None)

任何DatetimeIndex类型都可以通过to_period()方法和一个频率代码转换成PeriodIndex类型。

用'D'将数据转换成单日的时间序列：

In [74]:

dates.to_period('D')

Out[74]:

PeriodIndex(['2020-07-03', '2020-07-04', '2020-07-06', '2020-07-07',
             '2020-07-08'],
            dtype='period[D]', freq='D')

当用一个日期减去另一个日期时，返回的结果是TimedeltaIndex类型：

In [75]:

dates - dates[0]

Out[75]:

TimedeltaIndex(['0 days', '1 days', '3 days', '4 days', '5 days'], dtype='timedelta64[ns]', freq=None)

有规律的时间序列：`pd.date_range()`¶

为了能更简便地创建有规律的时间序列，Pandas提供了一些方法：pd.date_range()可以处理时间戳、pd.period_range()可以处理周期、pd.timedelta_range()可以处理时间间隔。通过开始日期、结束日期和频率代码（同样是可选的）创建一个有规律的日期序列，默认的频率是天：

In [76]:

 pd.date_range('2020-07-03', '2020-07-10')  

Out[76]:

DatetimeIndex(['2020-07-03', '2020-07-04', '2020-07-05', '2020-07-06',
               '2020-07-07', '2020-07-08', '2020-07-09', '2020-07-10'],
              dtype='datetime64[ns]', freq='D')

日期范围不一定非是开始时间与结束时间，也可以是开始时间与周期数periods：

In [77]:

pd.date_range('2020-07-03', periods=8)

Out[77]:

DatetimeIndex(['2020-07-03', '2020-07-04', '2020-07-05', '2020-07-06',
               '2020-07-07', '2020-07-08', '2020-07-09', '2020-07-10'],
              dtype='datetime64[ns]', freq='D')

通过freq参数改变时间间隔，默认值是D。例如，可以创建一个按小时变化的时间戳：

In [78]:

pd.date_range('2020-07-03', periods=8, freq='H')  

Out[78]:

DatetimeIndex(['2020-07-03 00:00:00', '2020-07-03 01:00:00',
               '2020-07-03 02:00:00', '2020-07-03 03:00:00',
               '2020-07-03 04:00:00', '2020-07-03 05:00:00',
               '2020-07-03 06:00:00', '2020-07-03 07:00:00'],
              dtype='datetime64[ns]', freq='H')

如果要创建一个有规律的周期或时间间隔序列，有类似的函数pd.period_range()和pd.timedelta_range()。下面是一个以月为周期的示例：

In [79]:

pd.period_range('2020-07', periods=8, freq='M')
 

Out[79]:

PeriodIndex(['2020-07', '2020-08', '2020-09', '2020-10', '2020-11', '2020-12',
             '2021-01', '2021-02'],
            dtype='period[M]', freq='M')

以小时递增：

In [80]:

pd.timedelta_range(0, periods=10, freq='H')

Out[80]:

TimedeltaIndex(['00:00:00', '01:00:00', '02:00:00', '03:00:00', '04:00:00',
                '05:00:00', '06:00:00', '07:00:00', '08:00:00', '09:00:00'],
               dtype='timedelta64[ns]', freq='H')

时间频率与偏移量¶

Pandas时间序列工具的基础是时间频率或偏移量（offset）代码。就像之前见过的D（day）和H（hour）代码，可以设置任意需要的时间间隔

代码	描述	代码	描述
`D`	天（calendar day，按日历算，含双休日）	`B`	天（business day，仅含工作日）
`W`	周（weekly）
`M`	月末（month end）	`BM`	月末（business month end，仅含工作日）
`Q`	季节末（quarter end）	`BQ`	季节末（business quarter end，仅含工作日）
`A`	年末（year end）	`BA`	年末（business year end，仅含工作日）
`H`	小时（hours）	`BH`	小时（business hours，工作时间）
`T`	分钟（minutes）
`S`	秒（seconds）
`L`	毫秒（milliseonds）
`U`	微秒（microseconds）
`N`	纳秒（nanoseconds）

月、季、年频率都是具体周期的结束时间（月末、季末、年末），而有一些以S（start，开始）为后缀的代码表示日期开始。

代码	频率
`MS`	月初（month start）
`BMS`	月初（business month start，仅含工作日）
`QS`	季初（quarter start）
`BQS`	季初（business quarter start，仅含工作日）
`AS`	年初（year start）
`BAS`	年初（business year start，仅含工作日）

另外，可以在频率代码后面加三位月份缩写字母来改变季、年频率的开始时间：

Q-JAN、BQ-FEB、QS-MAR、BQS-APR等
A-JAN、BA-FEB、AS-MAR、BAS-APR等

也可以在后面加三位星期缩写字母来改变一周的开始时间：

W-SUN、W-MON、W-TUE、W-WED等

还可以将频率组合起来创建的新的周期。例如，可以用小时（H）和分钟（T）的组合来实现2小时30分钟：

In [81]:

pd.timedelta_range(0, periods=9, freq="2H30T")

Out[81]:

TimedeltaIndex(['00:00:00', '02:30:00', '05:00:00', '07:30:00', '10:00:00',
                '12:30:00', '15:00:00', '17:30:00', '20:00:00'],
               dtype='timedelta64[ns]', freq='150T')

所有这些频率代码都对应Pandas时间序列的偏移量，具体内容可以在pd.tseries.offsets模块中找到。例如，可以用下面的方法直接创建一个工作日偏移序列：

In [82]:

from pandas.tseries.offsets import BDay
pd.date_range('2020-07-01', periods=5, freq=BDay())

Out[82]:

DatetimeIndex(['2020-07-01', '2020-07-02', '2020-07-03', '2020-07-06',
               '2020-07-07'],
              dtype='datetime64[ns]', freq='B')

重采样、时间迁移和窗口函数¶

下面用贵州茅台的历史股票价格演示：

In [1]:

%%file snowball.py
from datetime import datetime
import requests
import pandas as pd


def get_stock(code):
    response = requests.get(
        "https://stock.xueqiu.com/v5/stock/chart/kline.json",
        headers={
            "User-Agent": "Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_4) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/81.0.4044.138 Safari/537.36"
        },
        params=(
            ("symbol", code),
            ("begin", int(datetime.now().timestamp() * 1000)),
            ("period", "day"),
            ("type", "before"),
            ("count", "-5000"),
            ("indicator", "kline"),
        ),
        cookies={"xq_a_token": "328f8bbf7903261db206d83de7b85c58e4486dda",},
    )

    if response.ok:
        d = response.json()["data"]
        data = pd.DataFrame(data=d["item"], columns=d["column"])
        data.index = data.timestamp.apply(
            lambda _: pd.Timestamp(_, unit="ms", tz="Asia/Shanghai")
        )
        return data
    else:
        print("stock error")

Writing snowball.py

In [4]:

from snowball import get_stock

data = get_stock("SH600519")  # 贵州茅台

data.tail()

Out[4]:

	timestamp	volume	open	high	low	close	chg	percent	turnoverrate	amount	volume_post	amount_post
timestamp
2020-05-08 00:00:00+08:00	1588867200000	2907868	1317.0	1338.00	1308.51	1314.61	2.61	0.20	0.23	3.839218e+09	None	None
2020-05-11 00:00:00+08:00	1589126400000	2367119	1320.0	1335.00	1313.67	1323.01	8.40	0.64	0.19	3.135991e+09	None	None
2020-05-12 00:00:00+08:00	1589212800000	1972181	1318.0	1334.99	1316.00	1333.00	9.99	0.76	0.16	2.621825e+09	None	None
2020-05-13 00:00:00+08:00	1589299200000	2201431	1333.0	1337.99	1322.88	1335.95	2.95	0.22	0.18	2.931465e+09	None	None
2020-05-14 00:00:00+08:00	1589385600000	1857492	1330.0	1334.88	1325.11	1326.59	-9.36	-0.70	0.15	2.467976e+09	None	None

In [2]:

gzmt = data['close']

In [99]:

gzmt.plot(figsize=(15,8));
plt.title('贵州茅台历史收盘价');

重采样与频率转换¶

按照新的频率（更高频率、更低频率）对数据进行重采样，可以通过resample()方法、asfreq()方法。

resample()方法是以数据累计（data aggregation）为基础
asfreq()方法是以数据选择（data selection）为基础。

用两种方法对数据进行下采样（down-sample，减少采样频率，从日到月）。用每年末（'BA'，最后一个工作日）对数据进行重采样：

In [100]:

plt.figure(figsize=(15, 8))
gzmt.plot(alpha=0.5, style="-")
gzmt.resample("BA").mean().plot(style=":")
gzmt.asfreq("BA").plot(style="--")
plt.title('贵州茅台历史收盘价年末采样');
plt.legend(["input", "resample", "asfreq"], loc="upper left");

在每个数据点上，resample反映的是上一年的均值，而asfreq反映的是上一年最后一个工作日的收盘价。

在进行上采样（up-sampling，增加采样频率，从月到日）时，resample()与asfreq()的用法大体相同，

两种方法都默认将采样作为缺失值NaN，与pd.fillna()函数类似，asfreq()有一个method参数可以设置填充缺失值的方式。对数据按天进行重采样（包含周末），asfreq()向前填充与向后填充缺失值的结果对比：

In [112]:

fig, ax = plt.subplots(2, sharex=True, figsize=(15, 8))
data = gzmt.iloc[-14:]

ax[0].set_title("贵州茅台近两周收盘价")
data.asfreq("D").plot(ax=ax[0], marker="o")

ax[1].set_title("采样缺失值填充方法对比")

data.asfreq("D", method="bfill").plot(ax=ax[1], style="-o")
data.asfreq("D", method="ffill").plot(ax=ax[1], style="--o")
ax[1].legend(["back-fill", "forward-fill"]);

时间迁移¶

Pandas提供shift()方法迁移数据，tshift()方法迁移索引。两种方法都是按照频率代码进行迁移。

用shift()和tshift()这两种方法让数据迁移900天：

In [114]:

fig, ax = plt.subplots(3, sharey=True, figsize=(15, 8))

# 对数据应用时间频率，用向后填充解决缺失值
gzmt = gzmt.asfreq("D", method="pad")

gzmt.plot(ax=ax[0])
gzmt.shift(900).plot(ax=ax[1])
gzmt.tshift(900).plot(ax=ax[2])

# 设置图例与标签
local_max = pd.to_datetime("2010-01-01")
offset = pd.Timedelta(900, "D")

ax[0].legend(["input"], loc=2)
ax[0].get_xticklabels()[5].set(weight="heavy", color="red")
ax[0].axvline(local_max, alpha=0.3, color="red")

ax[1].legend(["shift(900)"], loc=2)
ax[1].get_xticklabels()[5].set(weight="heavy", color="red")
ax[1].axvline(local_max + offset, alpha=0.3, color="red")

ax[2].legend(["tshift(900)"], loc=2)
ax[2].get_xticklabels()[1].set(weight="heavy", color="red")
ax[2].axvline(local_max + offset, alpha=0.3, color="red");

Python数据科学分享——2.数据处理¶

Numpy¶

神经网络示例¶

背景¶

网络图¶

数学描述¶

反向传播¶

numpy实现¶

数据结构¶

数组初始化¶

通用函数(universal functions, ufunc)¶

数组的运算¶

特殊ufunc¶

高级特性¶

累计¶

外积¶

广播(Broadcasting)¶

Scipy稀疏矩阵¶

稀疏矩阵初始化¶

按坐标创建稀疏矩阵¶

数据压缩¶

COO合计转换¶

2X2混淆矩阵¶

Pandas¶

Series 与 Dataframe¶

向量化字符串操作¶

字符串方法¶

正则表达式¶

其他字符串方法¶

向量化字符串的取值与切片操作¶

指标变量¶

处理时间序列¶

Pandas的日期与时间工具¶

Pandas时间序列：用时间作索引¶

Pandas时间序列数据结构¶

有规律的时间序列：pd.date_range()¶

时间频率与偏移量¶

重采样、时间迁移和窗口函数¶

重采样与频率转换¶

时间迁移¶

Pandas ¶

向量化字符串操作 ¶

有规律的时间序列：`pd.date_range()`¶