Notebook

Circuit optimization using PatternManager - example of QAOA for MaxCut¶

This notebook provides an example of minimizing the duration of a quantum circuit. In this notebook, a quantum circuit implementing an instance of Q.A.O.A. is used and the PatternManager tool will be used to minimize the duration of this circuit. Since the purpose of this notebook is to explain the optimization tool PatternManager, details on the implementation of the circuit are not explained.

In this notebook, a variational circuit is used to solve MaxCut for the graph printed below. Solving MaxCut for a graph $\mathcal{G} = (\mathcal{V}, \mathcal{E})$ consists in finding a subset $S$ of $\mathcal{V}$ such as the number of edges in $\mathcal{E}$ linking a vertex of $S$ to a vertex of $\mathcal{V} \backslash S$ is maximal.

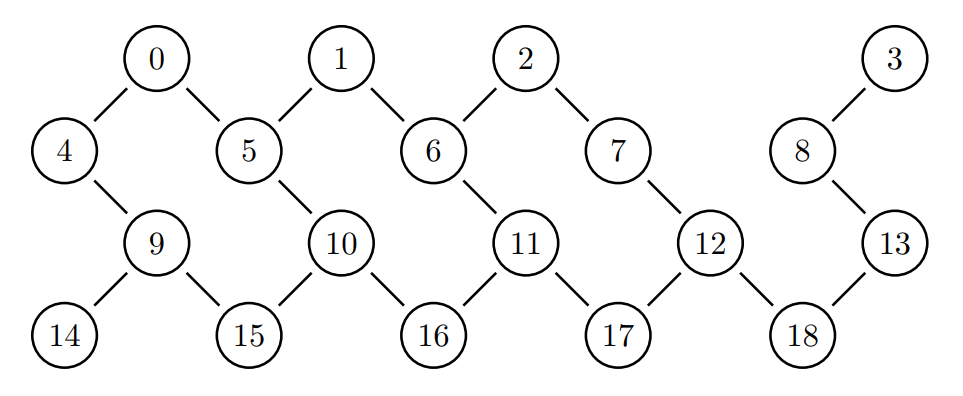
The circuit used in this example can be split in 3 parts:

An Hadamard gate on each qubit
For each pair of qubits $i$ and $j$, there is an E gate if and only if $i$ and $j$ are connected in the graph above
An $R_X$ on each qubit

An E gate can be defined by the following pattern:

Our circuit (limited to the first 8 qubits) looks like:

Initial circuit¶

The circuit should be created before starting the optimization. The following code defines an abstract gate E corresponding to the definition above. The circuit is then defined using these E gates. Since PatternManager is used to optimize the depth of the circuit, the initial order of E corresponds to the order which maximizes the duration of the circuit.

In [ ]:

from qat.lang.AQASM import Program, H, CNOT, PH, RX, QRoutine
from qat.lang.AQASM.misc import build_gate
from qat.pbo.utils import depth
import numpy as np


# Define an abstract gate E
@build_gate("E", [float], 2)
def E(alpha):
    """
    Build a E gate
    """
    routine = QRoutine()
    routine.apply(CNOT, [0, 1])
    routine.apply(PH(alpha), [1])
    routine.apply(CNOT, [0, 1])


# Define the worst order of E gates
edges = [(10, 15), (9, 15), (9, 14), (4, 9), (0, 4), (0, 5),
         (1, 5), (5, 10), (10, 16), (11, 16), (11, 17),
         (6, 11), (1, 6), (2, 6), (2, 7), (7, 12), (12, 17),
         (12, 18), (13, 18), (8, 13), (3, 8)]

# Define program
prog = Program()
qbits = prog.qalloc(19)
alpha = prog.new_var(float, r"\alpha")
beta = prog.new_var(float, r"\beta")

# Wall of hadamard
for qb in qbits:
    prog.apply(H, qb)
    
# E gates
for vertex_1, vertex_2 in edges:
    prog.apply(E(alpha), qbits[vertex_1], qbits[vertex_2])
    
# Wall of RX
for qb in qbits:
    prog.apply(RX(beta), qb)

# Get initial circ
initial_circ = prog.to_circ()
initial_circ.display()

Using metrics¶

The tool PatternManager is used to optimize any score function given by the user. A score function is a function that that the user wants to maximize. The qat.nnize modules provide tools to define score functions.

The DurationMetric class can be used as a score function, this class will compute the opposite of the duration of the circuit (this tool computes the opposite of the duration because maximizing the opposite of the duration is equivalent to minimizing the duration: the opposition of the duration is then the metric we want to maximize).

In our example, each gate will have the same duration: 1 unit of time.

In [ ]:

from qat.nnize.metrics import DurationMetric

# Define the metric
duration_metric = DurationMetric()

# Define the default duration
duration_metric.set_gate_time({"-DEFAULT-": 1})

# The metric has to compute the duration of the circuit
duration_metric.minimize_overall_time()

# Duration of the initial circuit
print("Duration of the initial circuit:",
      -duration_metric(initial_circ))

Circuit optimization¶

The optimization problem consists in maximizing the function duration_metric. This function is called global metric, the tool PatternManager will use this metric to perform the optimization.

Since E gates commute on any qubits, few rules will be defined. The tool PatternManager will use these rules to optimize the duration of the circuit. The rules are defined by:

There are 3 commutation rules above, so 3 groups will be defined for the optimizer. A group is a set of equivalent patterns (i.e. a small subcircuit), the optimizer can replace any pattern in the circuit by a pattern of the same group. Groups define the action space of the optimizer.

PatternManager will use an heuristic to perform the optimization. Two different methods may be used:

The gradient descent (use "gradient") $\rightarrow$ Used by default
The simulated annealing (use "annealing") $\rightarrow$ Used here

In [ ]:

from qat.pbo import PatternManager, VAR
from qat.lang.AQASM import AbstractGate

# Define the optimizer
manager = PatternManager(global_metric=duration_metric)

# Define abstract variables
theta = VAR()
gamma = VAR()

# Group 1 - first commutation rule
group1 = manager.new_group()
# The following two lines define interchangeable patterns
group1.add_pattern([('E', [1, 2], theta), ('E', [0, 1], gamma)])
group1.add_pattern([('E', [0, 1], gamma), ('E', [1, 2], theta)])

# Group 2 - second commutation rule
group2 = manager.new_group()

group2.add_pattern([('E', [0, 1], theta), ('E', [0, 2], gamma)])
group2.add_pattern([('E', [0, 2], gamma), ('E', [0, 1], theta)])

# Group 3 - third commutation rule
group3 = manager.new_group()

x3 = VAR()
group3.add_pattern([('E', [0, 2], theta), ('E', [1, 2], gamma)])
group3.add_pattern([('E', [1, 2], gamma), ('E', [0, 2], theta)])

The optimizer can be then called on the circuit to minimize the duration of the circuit. A trace can be passed to the optimizer to log the values of the metric during the optimization.

Since the E gate is not a common gate, the constructor of the E gate should be given to the optimizer.

In [ ]:

# Create a trace list
trace = list()

# Add E gate constructor
manager.add_abstract_gate(E)

# Start optimization
final_circ = manager.replace_pattern(initial_circ, method='annealing', trace=trace)

# Print final circuit
print("Final duration:", -duration_metric(final_circ))

The trace of the optimization can be plotted using matplotlib.

In [ ]:

import matplotlib.pyplot as plt

plt.figure(figsize=(10, 5))
plt.xlabel("Nb iterations")
plt.ylabel("Duration")
plt.plot(range(len(trace)), [-depth for depth in trace])
plt.show()

Compilation¶

Before starting compilation, E gates must be replaced by their implementation. The GraphCircuit tool will be used to replace E gates.

In [ ]:

from qat.pbo import GraphCircuit

# Init graph circuit
theta = VAR()
graph = GraphCircuit()
graph.load_circuit(final_circ)

# Replace pattern
graph.replace_pattern(
    [("E", [0, 1], theta)],
    [("CNOT", [0, 1]), ("PH", [1], theta), ("CNOT", [0, 1])],
    pos=all
)

# Get circuit
final_circ = graph.to_circ()

One wants to compile this optimized circuit on the Rigetti Forest 19Q. Only few gates may be used on this quantum computer. The allowed gates are:

Gate $R_Z(x)$ for $x \in \mathbb{R}$
Gate $R_X(x)$ for $x \in \left\{ \pm \pi, \pm \frac{\pi}{2} \right\}$ (these $R_X$ gates are called "compliant $R_X$")
Gate $CZ$

Since our algorithm does not use these gates, some changes may be defined. PatternManager could be used to solve this optimization problem. It is possible to define patterns which must disappear.

The gate $PH$ must disappear: $PH(x) \rightarrow R_Z(x)$
The gate $H$ must disappear: $H \rightarrow R_Z \left (\frac{\pi}{2} \right) \cdot R_X \left (\frac{\pi}{2} \right) \cdot R_Z \left (\frac{\pi}{2} \right)$
The gate $CNOT$ must disappear: $CNOT \rightarrow \left(\mathbb{1} \otimes H \right) \cdot CZ \cdot \left(\mathbb{1} \otimes H \right)$

Groups¶

Group 1 Only non-compliant $R_X(x)$ are transformed into $H \cdot R_Z(x) \cdot H$

Group 2 $PH(x)$ gates are replaced by $R_Z(x)$ gates

Group 3 $CNOT$ gates are replaced by $(\mathbb{1} \otimes H) \cdot CZ \cdot (\mathbb{1} \otimes H)$

Group 4 $H$ gates are replaced by $R_Z \left (\frac{\pi}{2} \right) \cdot R_X \left (\frac{\pi}{2} \right) \cdot R_Z \left (\frac{\pi}{2} \right)$

In [ ]:

from math import pi

# Define a compiler: no metric needed
compiler = PatternManager()
theta = VAR()

# Group 1: remove non compliant RX gates
constraint_angle = VAR()

for angle in [pi, -pi, pi/2, -pi/2]:
    constraint_angle.add_prohibited_value(angle)
    
group_1 = compiler.new_group()

group_1.pattern_to_remove([("RX", [0], constraint_angle)])
group_1.add_pattern([("H", [0]), ("RZ", [0], constraint_angle), ("H", [0])])

# Group 2: remove PH gate
group_2 = compiler.new_group()

group_2.pattern_to_remove([("PH", [0], theta)])
group_2.add_pattern([("RZ", [0], theta)])

# Group 3: remove CNOT
group_3 = compiler.new_group()

group_3.pattern_to_remove([("CNOT", [0, 1])])
group_3.add_pattern([("H", [1]), ("CSIGN", [0, 1]), ("H", [1])])

# Group 4: remove H
group_4 = compiler.new_group()

group_4.pattern_to_remove([("H", [0])])
group_4.add_pattern([("RZ", [0], pi/2), ("RX", [0], pi/2), ("RZ", [0], pi/2)])

The object compiler can be used to compile our circuit. Moreover, this object is also a plugin, it can be linked to any QPU.

Checking compilation¶

First, a function which prints the gate set will be used to check the compilation output:

In [ ]:

from qat.core.util import extract_syntax

def print_gate_set(circuit):
    gate_set = set()
    
    for operator in circuit.ops:
        name, params = extract_syntax(
            circuit.gateDic[operator.gate],
            circuit.gateDic
        )
        gate_set.add((name, *params))
        
    print(gate_set)

Then, our compiler can compile our circuit using:

in the first example, RX gates with accepted angles
in the second example, RX gates with non-accepted angles

In [ ]:

# Case 1: using RX gates with accepted angles
first_circ = compiler.replace_pattern(
    final_circ.bind_variables({r"\alpha": pi/4, r"\beta": pi})
)

print("\nCase 1 with compliant RX")
print_gate_set(first_circ)

# Case 2: using RX gates with non accepted angles
second_circ = compiler.replace_pattern(
    final_circ.bind_variables({r"\alpha": pi/4, r"\beta": pi/6})
)

print("\nCase 2 with non-compliant RX")
print_gate_set(second_circ)

In [ ]: