The goal of this presentation is to familiarize you with some broad classes of neuroimaging data that can be interacted with in Python, using the NiBabel library.
This document is intended to be viewed as a RISE presentation. It works fine as a notebook, but blocks with images may look strange because they are formatted to work as slides.
NiBabel¶
NiBabel is a low-level Python library that gives access to a variety of imaging formats, with a particular focus on providing a common interface to the various volumetric formats produced by scanners and used in common neuroimaging toolkits:
| NIfTI-1 | NIfTI-2 | MGH |
| MINC 1.0 | MINC 2.0 | AFNI BRIK/HEAD |
| ANALYZE | SPM99 ANALYZE | SPM2 ANALYZE |
| DICOM | PAR/REC | ECAT |
It also supports surface file formats:
| GIFTI | FreeSurfer (FS) geometry |
| FS labels | FS annotations |
Tractography files:
| TrackVis (TRK) | MRtrix (TCK) |
As well as the CIFTI-2 format for composite volume/surface data.
Installation¶
NiBabel is available on PyPI:
pip install nibabel
And conda-forge:
conda install -c conda-forge nibabel
Note: This notebook assumes NiBabel 3+, which requires a minimum Python version of 3.5.
import nibabel as nb
print(nb.__version__)
# Some additional, useful imports
from pathlib import Path # Combine path elements with /
from pprint import pprint # Pretty-printing
import numpy as np # Numeric Python
from matplotlib import pyplot as plt # Matlab-ish plotting commands
from nilearn import plotting as nlp # Nice neuroimage plotting
import transforms3d # Work with affine algebra
from scipy import ndimage as ndi # Operate on N-dimensional images
import nibabel.testing # For fetching test data
%pylab inline
# Assume we're on the NeuroHackademy hub.
data_dir = Path('/home/jovyan/data')
Learning objectives¶
- Be able to load and save different types of files in NiBabel
- Become familiar with the
SpatialImageAPI and identify its components - Understand the differences between array and proxy images
- Acquire a passing familiarity with the structures of surface images, CIFTI-2 files, and tractograms
t1w = nb.load(data_dir / 'openneuro/ds000114/sub-01/ses-test/anat/sub-01_ses-test_T1w.nii.gz')
bold = nb.load(data_dir / 'openneuro/ds000114/sub-01/ses-test/func/sub-01_ses-test_task-fingerfootlips_bold.nii.gz')
print(t1w)
Saving¶
All NiBabel images have a .to_filename() method:
t1w.to_filename('/tmp/img.nii.gz')
nibabel.save will attempt to convert to a reasonable image type, if the extension doesn't match:
nb.save(t1w, '/tmp/img.mgz')
Some image types separate header and data into two separate images. Saving to either filename will generate both.
nb.save(t1w, '/tmp/img.img')
print(nb.load('/tmp/img.hdr'))
Serialization¶
Some NiBabel images can be serialized to and deserialized from byte strings, for performing stream-based I/O.
bstr = t1w.to_bytes()
print(bstr[:100])
new_t1w = nb.Nifti1Image.from_bytes(bstr)
Images that save to single files can generally be serialized. NIfTI-1/2, GIFTI and MGH are currently supported.
Spatial Images¶
For MRI studies, neuroimaging data is typically acquired as one or more volumes, a regular grid of values. NiBabel represents these data as spatial images, a structure containing three things:
- The image data array: a 3D or 4D array of image data
- An affine matrix: 4x4 array relating voxel coordinates and "world" coordinates
- Image metadata: usually a format-specific header
Many file types encode this basic structure. NiBabel will read any of ANALYZE (plain, SPM99, SPM2 and later), NIfTI-1, NIfTI-2, MINC 1.0, MINC 2.0, AFNI BRIK/HEAD, MGH, ECAT, DICOM and Philips PAR/REC, and expose a simple interface:
data = t1w.get_fdata()
affine = t1w.affine
header = t1w.header
Spatial images have some properties that should be familiar from NumPy arrays:
print(t1w.ndim)
print(t1w.shape)
The data array¶
The data is a simple NumPy array. It can be accessed, sliced and generally manipulated as you would any array:
print(data.shape)
i, j, k = np.array(data.shape) // 2
fig, axes = plt.subplots(1, 3)
axes[0].imshow(data[i,:,:].T, cmap='Greys_r', origin='lower')
axes[1].imshow(data[:,j,:].T, cmap='Greys_r', origin='lower')
_ = axes[2].imshow(data[:,:,k].T, cmap='Greys_r', origin='lower')
Each location in the image data array is a voxel (pixel with a volume), and can be referred to with voxel coordinates (array indices).
This is a natural way to describe a block of data, but is practically meaningless with regard to anatomy.
NiBabel has a basic viewer that scales voxels to reflect their size and labels orientations.
_ = t1w.orthoview() # Requires matplotlib, occasionally glitchy in OSX setups
The crosshair is focused at the origin $(0, 0, 0)$.
All of this information is encoded in the affine:
print(affine)
Affine transforms¶
The affine is a 4 x 4 numpy array. This describes the transformation from the voxel space (indices $(i, j, k)$) to a reference space (coordinates $(x, y, z)$). These coordinates are, by convention, distance in mm right, anterior and superior of an origin*.
$$ \begin{bmatrix} x\\ y\\ z\\ 1\\ \end{bmatrix} = \mathbf A \begin{bmatrix} i\\ j\\ k\\ 1\\ \end{bmatrix} =\begin{bmatrix} m_{1,1} & m_{1,2} & m_{1,3} & a \\ m_{2,1} & m_{2,2} & m_{2,3} & b \\ m_{3,1} & m_{3,2} & m_{3,3} & c \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} i\\ j\\ k\\ 1\\ \end{bmatrix} $$For an unmodified image, this reference space typically refers to an origin in the isocenter of the imaging magnet, and the directions right, anterior and superior are defined assuming a subject is lying in the scanner, face up.
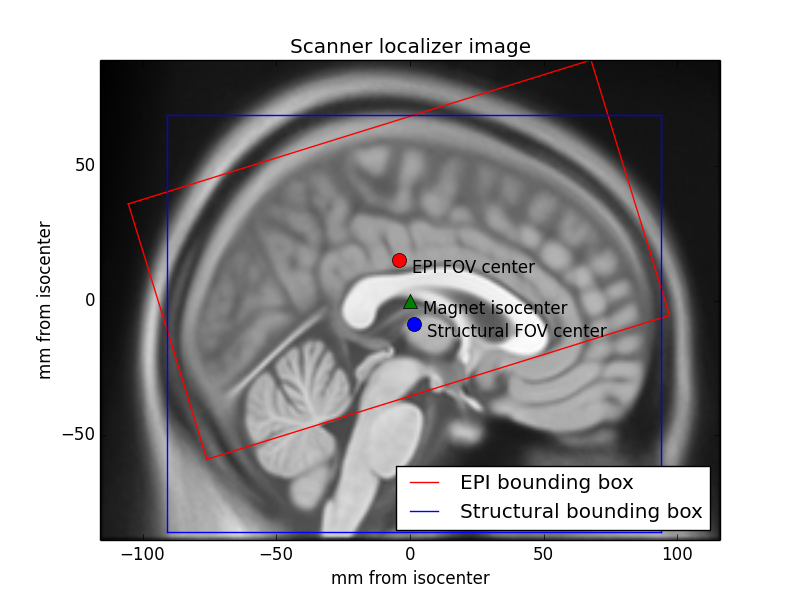
* If a file format uses an alternative convention, NiBabel converts on read/write, so affines are always RAS+.
The affine as a series of transformations¶
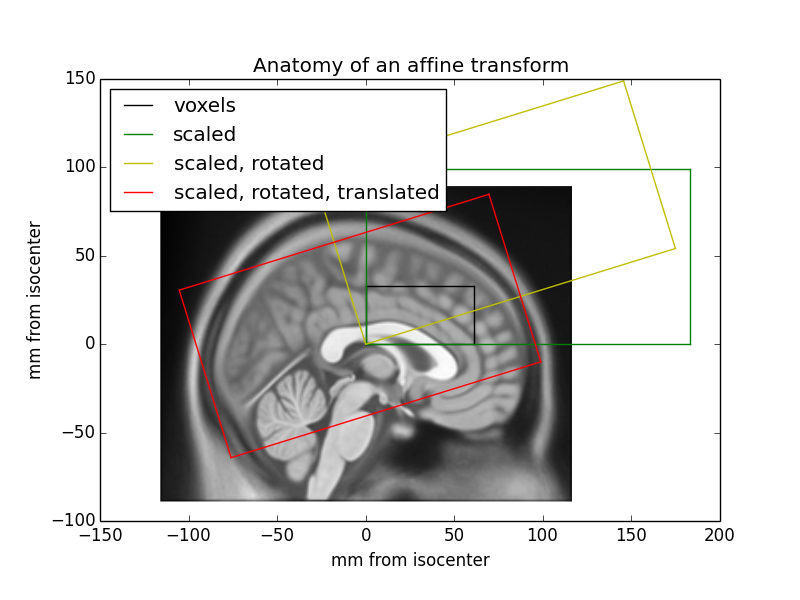
An affine transformation can be decomposed into translation, rotation, scaling (zooms) and shear transformations, applied right-to-left.
T, R, Z, S = transforms3d.affines.decompose44(affine) # External library
print(f"Translation: {T}\nRotation:\n{R}\nZooms: {Z}\nMax shear: {np.abs(S).max()}")
Tm, Rm, Zm, Sm = [np.eye(4) for _ in range(4)]
Tm[:3, 3] = T
Rm[:3, :3] = R
Zm[:3, :3] = np.diag(Z)
Sm[[0, 0, 1], [1, 2, 2]] = S
np.allclose(Tm @ Rm @ Zm @ Sm, affine)
NiBabel provides functions for extracting information from affines:
- Orientation (or axis codes) indicates the direction an axis encodes. If increasing index along an axis moves to the right or left, the axis is coded "R" or "L", respectively.
- Voxel sizes (or zooms)
- Obliquity measures the amount of rotation from "canonical" axes.
print("Orientation:", nb.aff2axcodes(affine))
print("Zooms:", nb.affines.voxel_sizes(affine))
print("Obliquity:", nb.affines.obliquity(affine))
You can also use it to answer specific questions. For instance, the inverse affine allows you to calculate indices from RAS coordinates and look up the image intensity value at that location.
i, j, k, _ = np.linalg.pinv(affine) @ [0, 0, 0, 1]
print(f"Center: ({int(i)}, {int(j)}, {int(k)})")
print(f"Value: ", data[int(i), int(j), int(k)])
Don't Panic¶
If you didn't follow all of the above, that's okay. Here are the important points:
- Affines provide the spatial interpretation of the data.
- NiBabel has some useful methods for working with them.
You'll go over this again with Noah Benson in Introduction to the Geometry and Structure of the Human Brain.
Matthew Brett's Coordinate systems and affines tutorial is an excellent resource.
Image headers¶
The image header is specific to each file format. Minimally, it contains information to construct the data and affine arrays, but some methods are useful beyond that.
get_zooms()method returns voxel sizes. If the data is 4D, then repetition time is included as a temporal zoom.get_data_dtype()returns the numpy data type in which the image data is stored (or will be stored when the image is saved).
print(bold.header.get_zooms())
print(bold.header.get_data_dtype())
For images with fixed header structures, header fields are exposed through a dict-like interface.
print(header)
print(header['descrip'])
The MGH header is similarly accessible, but its structure is quite different:
mghheader = nb.load('/tmp/img.mgz').header
print(mghheader)
print(mghheader['Pxyz_c'])
print(mghheader.get_zooms())
print(mghheader.get_data_dtype())
Other formats use text key-value pairs (PAR/REC, BRIK/HEAD) or keys in NetCDF (MINC 1.0) or HDF5 (MINC 2.0) containers, and their values are accessible by other means.
Often, we're not particularly interested in the header, or even the affine. But it's important to know they're there and, especially, to remember to copy them when making new images, so that derivatives stay aligned with the original image.
Creating new images¶
Reading data will only take you so far. In many cases, you will want to use the image to compute a new image in the same space. Such a function might take the form:
def my_function(image):
orig_data = image.get_fdata()
new_data = some_operation_on(orig_data)
return image.__class__(new_data, affine=image.affine, header=image.header)
Note the image.__class__ ensures that the output image is the same type as the input. If your operation requires specific format features, you might use a specific class like nb.Nifti1Image.
For example, perhaps we want to save space and rescale our T1w image to an unsigned byte:
def rescale(img):
data = img.get_fdata()
rescaled = ((data - data.min()) * 255. / (data.max() - data.min())).astype(np.uint8)
rescaled_img = img.__class__(rescaled, affine=img.affine, header=img.header)
rescaled_img.header.set_data_dtype('uint8') # Ensure data is saved as this type
return rescaled_img
rescaled_t1w = rescale(t1w)
rescaled_t1w.to_filename('/tmp/rescaled_t1w.nii.gz')
Data objects - Arrays and Array Proxies¶
Recall that the spatial image contains data, affine and header objects. When creating a new image, the data array is typically an array.
array_img = nb.Nifti1Image(np.arange(244, 268).reshape(2, 3, 4), affine=np.diag([2, 2, 2, 1]))
print(array_img.dataobj)
When loading a file, an ArrayProxy is used for most image types.
array_img.to_filename('/tmp/array_img.nii')
proxy_img = nb.load('/tmp/array_img.nii')
print(proxy_img.dataobj)
An array proxy is an object that knows how to access data, but does not read it until requested. The usual way to request data is get_fdata(), which returns all data as floating point:
proxy_img.get_fdata(dtype=np.float32) # The default is float64, but you can choose any floating point type.
get_fdata() provides a very predictable interface. When you need more control, you'll want to work with the ArrayProxy directly.
Converting array proxies to arrays¶
Array proxies are designed to be one step away from a numpy array:
arr = np.asanyarray(proxy_img.dataobj) # array will create a copy; asarray passes through arrays; asanyarray passes subclasses like memmap through
print(arr.dtype)
arr
Memory maps are arrays that remain on disk, rather than in RAM. This is only possible with uncompressed images.
We can also cast to any type we please, however unwisely.
print(np.uint8(proxy_img.dataobj)) # Values over 255 will be truncated
print(np.complex256(proxy_img.dataobj)) # A life less ordinal
Indexing and slicing array proxies¶
One of the primary motivations for an array proxy is to avoid loading data unnecessarily. Accessing the array proxy with array indices or slices will return the requested values without loading other data:
print(proxy_img.dataobj[0])
print(proxy_img.dataobj[..., 1:3])
For example, this is useful for fetching a single volume from a BOLD series:
vol0 = bold.dataobj[..., 0]
vol0.shape
Slicing works with compressed data, as well. Install the indexed-gzip package for significant speedups with gzipped files.
Scaling array proxies¶
Several image types, including NIfTI, have a slope and intercept (scaling factors) in the header that allows them to extend the data range and/or precision beyond those of the on-disk type.
For example uint16 can take the values 0-65535. If a BOLD series includes values from 500-2000, we can calculate a slope that will allow us to utilize the 16 bits of precision to encode our desired values.
pr = (500, 2000) # Plausible range
nbits = 16 # 16-bits of precision
scl_slope = (pr[1] - pr[0]) / (2 ** nbits) # Resolvable difference
scl_inter = pr[0] # Minimum value
print(scl_slope, scl_inter)
"Saving space by collapsing plotting into one line."; x = np.arange(2 ** nbits); plt.step(x, x * scl_slope + scl_inter); vlim = np.array([120, 150]); plt.xlim(vlim); plt.ylim(vlim * scl_slope + scl_inter); plt.xlabel("On-disk value"); plt.ylabel('"True" value'); _ = plt.show();
Let's create an image from some random values in our plausible range:
float_img = nb.Nifti1Image(np.random.default_rng().uniform(500, 2000, (2, 3, 4)), # 64-bit float
affine=np.diag([2, 2, 2, 1]))
print(float_img.get_fdata())
Save as uint16 and check its values:
float_img.header.set_data_dtype(np.uint16)
float_img.to_filename("/tmp/uint16_img.nii")
uint16_img = nb.load("/tmp/uint16_img.nii")
print(uint16_img.get_fdata())
We clearly lost some precision...
np.max(np.abs(float_img.get_fdata() - uint16_img.get_fdata()))
But what's going on?
The ArrayProxy keeps track of scaling factors:
print(f"Slope: {uint16_img.dataobj.slope}; Intercept: {uint16_img.dataobj.inter}")
print(uint16_img.dataobj.get_unscaled())
The scaling is done automatically when the data is accessed, by slice or whole.
print(np.asanyarray(uint16_img.dataobj))
print(uint16_img.dataobj[0, 0, 0])
The ArrayProxy guarantees that the data has the intended value, but the type can vary based on the on-disk type and the values of scaling factors.
print(proxy_img.dataobj[0, 0, 0].dtype) # Our earlier integer image
print(uint16_img.dataobj[0, 0, 0].dtype)
get_fdata() sweeps these details under the rug and always gives you the same type.
Don't Panic¶
If you didn't follow all of the above, that's okay. Here are the important points:
- When in doubt, use
img.get_fdata()will fetch all of the data, and it will always be a float img.dataobjexists if you want to load only some data or control the data type- Both methods transparently scale data when needed
In the NiBabel docs, The image data array gives you an overview of both methods, and Images and memory has even more details.
Slicing images¶
Slicing array proxies is nice. Wouldn't it be nicer to keep track of the affine and header?
The slicer attribute provides an interface that allows you to apply slices to an image, and updates the affine to ensure that the spatial information matches.
Consider the T1-weighted image from earlier:
_ = t1w.orthoview()
We can use the slicer to crop unneeded voxels in the left-right and inferior-superior directions:
cropped = t1w.slicer[40:216, :, 50:226]
cropped.orthoview()
Note the origin crosshair points to the same structure. The affines now differ in translation:
print(cropped.affine - t1w.affine)
You can even downsample an image, and the zooms will reflect the increased distance between voxels.
cheap_downsample = cropped.slicer[2::4, 2::4, 2::4]
print(cheap_downsample.header.get_zooms())
cheap_downsample.orthoview()
Note that this is a bad idea in most circumstances because it induces aliasing.
The better approach would be to anti-alias and then slice:
def blur(img, sigma): # Isotropic in voxel space, not world space
return img.__class__(ndi.gaussian_filter(img.dataobj, sigma), img.affine, img.header)
better_downsample = blur(cropped, sigma=1.5).slicer[2::4, 2::4, 2::4]
better_downsample.orthoview()
For non-spatial dimensions, slices or indices may be used to select one or more volumes.
tp15 = bold.slicer[..., :5]
tp1 = bold.slicer[..., 0]
print(f"BOLD shape: {bold.shape}; Zooms: {bold.header.get_zooms()}")
print(f"Time pts 1-5 shape: {tp15.shape}; Zooms: {tp15.header.get_zooms()}")
print(f"Time pt 1 shape: {tp1.shape}; Zooms: {tp1.header.get_zooms()}")
np.array_equal(tp15.get_fdata(), bold.dataobj[..., :5])
Aliasing considerations apply to time series as well, so be careful with down-sampling here, too.
Surface Images¶
Although the scanner samples data in three dimensions, some brain structures are better represented as a convoluted sheet than a volume. Data may be usefully resampled onto a cortical sheet, but in the process, it loses the intrinsic geometry of a 3D array.
To represent data on a surface, you need the following structures:
- The surface mesh
- Vertices: a list of coordinates in world space
- Faces: a list of 3-tuples of indices into the coordinate list
- The data array: a 1D or 2D array of values or vectors at each vertex
Unlike spatial images, these components are frequently kept in separate files.
Terminological note: You are likely to encounter multiple names for each of these. Vertices may be called coordinates or a point set. Faces are often called triangles. When a data array is plotted on the surface, it might be called a texture.
Image-specific interfaces¶
The two supported surface formats at present are GIFTI and FreeSurfer geometry files. Unlike spatial images, there is not yet a common interface for working with surface-based data.
FreeSurfer encodes a great deal of information in its directory structure and file names, allowing the necessary data arrays to have relatively simple formats.
GIFTI is more of an interchange format, and so has a rich metadata structure and can store different kinds of data.
Surface meshes¶
To load a surface mesh in a FreeSurfer directory, use nb.freesurfer.read_geometry:
fs_verts, fs_faces, fs_meta = nb.freesurfer.read_geometry(data_dir / 'ds005-preproc/freesurfer/sub-01/surf/lh.pial', read_metadata=True)
print(fs_verts[:2])
print(fs_faces[:2])
pprint(fs_meta)
NiBabel does not have any viewer for surfaces, but Nilearn has plotting utilities:
_ = nlp.plot_surf((fs_verts, fs_faces))
Let's do the same thing with GIFTI. Here, the file-level metadata is minimal:
gii_pial = nb.load(data_dir / 'ds005-preproc/fmriprep/sub-01/anat/sub-01_hemi-L_pial.surf.gii')
pprint(gii_pial.meta.metadata) # .meta maps onto the XML object, its .metadata property exposes a Python dict
The vertices and faces are stored as separate data arrays, each with their own metadata. These can be queried by NIfTI intent code:
pointset_darray = gii_pial.get_arrays_from_intent('pointset')[0]
triangle_darray = gii_pial.get_arrays_from_intent('triangle')[0]
pprint(pointset_darray.meta.metadata)
pprint(triangle_darray.meta.metadata)
The actual values are stored as the .data attribute:
gii_verts, gii_faces = pointset_darray.data, triangle_darray.data
print(gii_verts[:2])
print(gii_faces[:2])
This API can be cumbersome, if all you want is the NumPy arrays. Thanks to a project started at Neurohackademy 2019, the agg_data() (aggregate data) method will find the requested data array(s) and return just the data:
gii_verts, gii_faces = gii_pial.agg_data(('pointset', 'triangle'))
print(gii_verts[:2])
print(gii_faces[:2])
_ = nlp.plot_surf((gii_verts, gii_faces))
Surface-sampled data¶
For data sampled to the surface, FreeSurfer has a few data types:
# Morphometry
curv = nb.freesurfer.read_morph_data(data_dir / 'ds005-preproc/freesurfer/sub-01/surf/lh.curv')
# Annotations
labels, color_table, names = nb.freesurfer.read_annot(data_dir / 'ds005-preproc/freesurfer/sub-01/label/lh.aparc.annot')
# MGH files...
mgh = nb.load(data_dir / 'ds005-preproc/freesurfer/sub-01/surf/lh.w-g.pct.mgh')
print(curv.shape)
print(labels.shape)
print(mgh.shape)
fig, axes = plt.subplots(1, 3, subplot_kw={'projection': '3d'})
_ = nlp.plot_surf((fs_verts, fs_faces), curv, axes=axes[0])
_ = nlp.plot_surf((fs_verts, fs_faces), labels, axes=axes[1])
_ = nlp.plot_surf((fs_verts, fs_faces), mgh.get_fdata(), axes=axes[2])
GIFTIs will be GIFTIs. This one is a BOLD series sampled to the fsaverage5 surface:
bold_gii = nb.load(data_dir / 'ds005-preproc/fmriprep/sub-01/func/sub-01_task-mixedgamblestask_run-1_space-fsaverage5_hemi-L_bold.func.gii')
Each time point is an individual data array with intent NIFTI_INTENT_TIME_SERIES. agg_data() will aggregate these into a single array.
data = bold_gii.agg_data('time series')
data.shape
We can plot the mean BOLD signal. This time we will use a FreeSurfer surface, which Nilearn knows what to do with:
_ = nlp.plot_surf(str(data_dir / 'ds005-preproc/freesurfer/fsaverage5/surf/lh.inflated'), data.mean(axis=1))
Don't Panic¶
If you didn't follow all of the above, that's okay. Here are the important points:
- Practical considerations make dealing with surfaces a multi-file affair
- The data structures are common (vertices, faces, per-vertex data arrays), but the arrangement can vary
- For working with FreeSurfer files, learn to traverse the directory and identify file types
- For working with GIFTI, learn to query the file for its contents
Hopefully next year, we'll be able to talk about a common interface that will simplify things.
CIFTI-2¶
CIFTI-2 is a file format intended to cover many use cases for connectivity analysis.
Files have 2-3 dimensions and each dimension is described by one of 5 types of axis.
- Brain models: each row/column is a voxel or vertex
- Parcels: each row/column is a group of voxels and/or vertices
- Scalars: each row/column has a unique name
- Labels: each row/column has a unique name and label table
- Series: each row/column is a point in a series (typically time series), which increases monotonically
For example, a "parcellated dense connectivity" CIFTI-2 file has two dimensions, indexed by a brain models axis and a parcels axis, respectively. The interpretation is "connectivity from parcels to vertices and/or voxels".
On disk, the file is a NIfTI-2 file with an alternative XML header as an extension, schematized here.
NiBabel loads a header that closely mirrors this structure, and makes the NIfTI-2 header accessible as a nifti_header attribute.
cifti = nb.load(data_dir / 'ds005-preproc/fmriprep/sub-01/func/sub-01_task-mixedgamblestask_run-1_space-fsLR_den-91k_bold.dtseries.nii')
cifti_data = cifti.get_fdata(dtype=np.float32)
cifti_hdr = cifti.header
nifti_hdr = cifti.nifti_header
The Cifti2Header is useful if you're familiar with the XML structure and need to fetch an exact value or have fine control over the header that is written.
bm0 = next(cifti_hdr.matrix[1].brain_models)
print(bm0.voxel_indices_ijk)
print(list(bm0.vertex_indices)[:20])