Сравнение распределений от KL в эксперименте и моделировании¶
Методика для эффективности поиска KL¶
1. Отбор событий процесса $e^+e^- \to K_S K_L$¶
- отбираю KS согласно стандартной методике;
- ставлю дополнительные условия отбора $\text{kslen}>1$, $\text{ksalign}>0.95$, $|\text{ksth} - \pi/2|<0.6$, $|x_1|<20$ (чтоб отобрать чистые события без фона)
- объединяю отобранные события из всех точек одного сезона, чтоб увеличить выборку (события моделирования взвешены на количестве событий в эксперименте)
- сравниваю распределения по различным параметрам KS (полярный угол, инв. масса, импульс) в эксперименте и моделировании (см. ниже в ноутбуке)
- полученные выборки будут исходными, относительно которых я буду вычислять эффективность обнаружения KS
2. Эффективность поиска KL¶
- сравниваю распределения по пространственному углу ($\psi$) между ближайшим кластером к обратному импульсу KS (не должны отличаться, т.к. из эксперимента выделены чистые KSKL)
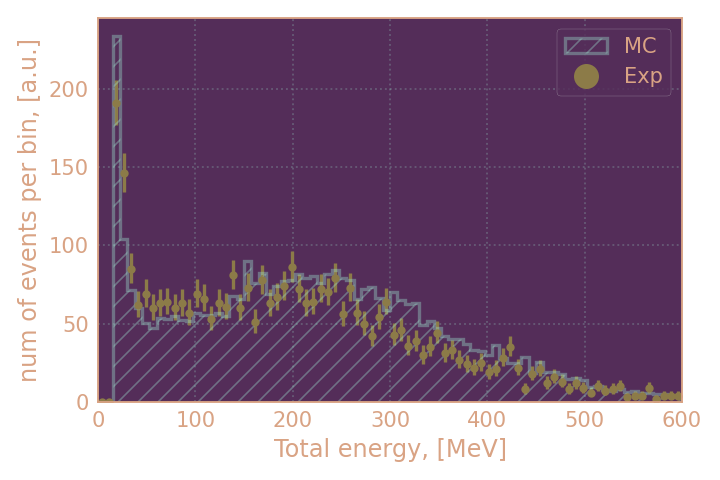
- сравниваю распределения по энерговыделению в LiXe калориметре ($E_{LiXe}$) и полному энерговыделению ($E_{tot}$) в кластере (не должны отличаться в идеале)
- теперь вопрос, что считать KL:
- либо $\psi < 0.2$ рад.
- либо $\psi < 0.2$ рад. и $E_{LiXe} > 50$ МэВ (я показываю оба случая, если расхождение есть, то во втором варианте оно будет только больше)
- вычисляю эффективность обнаружения KL как
$N_{passed}(p)$ - количество обнаруженных KL в зависимости от импульса KS ($p$), $N_{total}(p)$ - количество событий KSKL в чистой выборке (полученной после этапа 1) в зависимости от импульса KS ($p$)
таким образом можно считать, что $$\varepsilon_{\text{exp}} = P_{\text{exp}}(\text{KL}|\text{KS}), \varepsilon_{\text{MC}} = P_{\text{MC}}(\text{KL}|\text{KS}),$$ где $P(\text{KL}|\text{KS})$ - вероятность обнаружить KL при условии обнаружения KS
Результаты¶
Распределения¶
Сравниваю распределения по различным параметрам для событий эксперимента и моделирования после отборов событий процесса $e^+e^- \to K_S K_L$, описанных в методической части выше.
На картинках ниже показаны объединённые экспериментальные данные и MC сезонов HIGH19/RHO18 (моделирование взвешенно на количество событий в эксперименте для каждой точки по энергии)
- RHO18 - точки на $\phi$-мезоне
- HIGH19 - сезон высоких энергий выше 1.05 ГэВ в с.ц.м.
| Распределение отобранных событий по инвариантной массе KS, HIGH19 | Распределение отобранных событий по инвариантной массе KS, RHO18 |
|---|---|
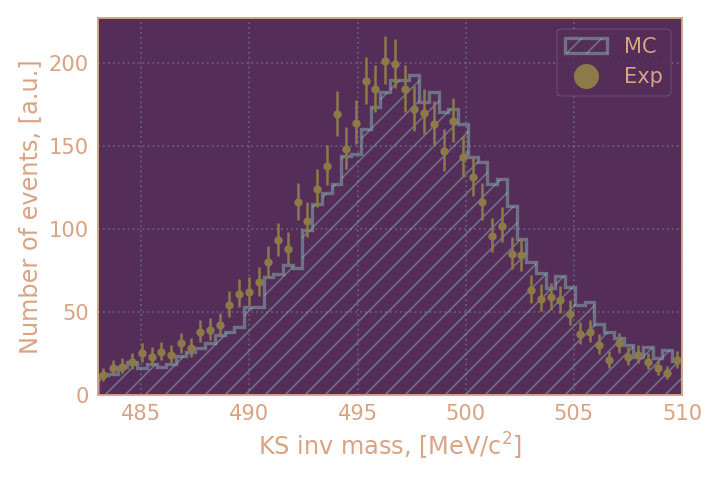 |
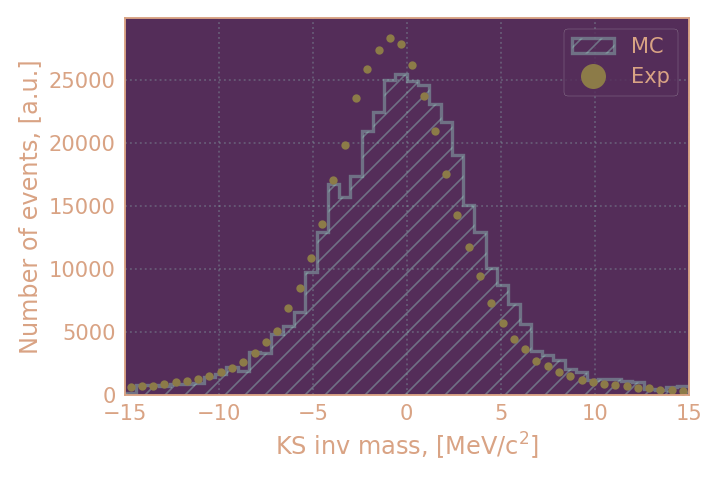 |
| Распределение отобранных событий по импульсу KS, HIGH19 | Распределение отобранных событий по импульсу KS, RHO18 |
|---|---|
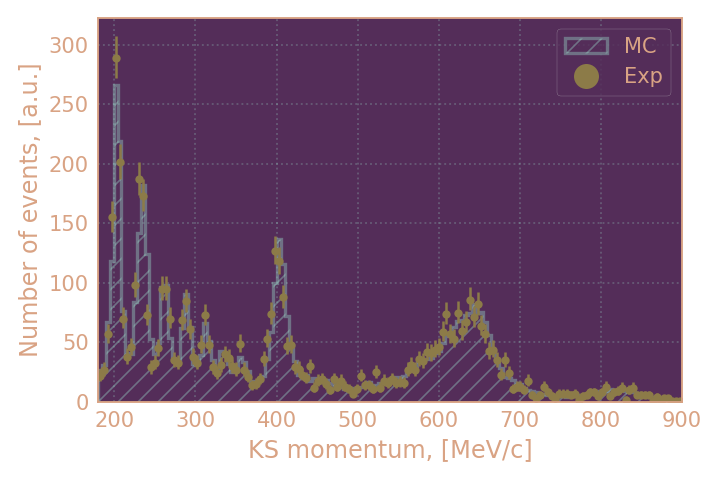 |
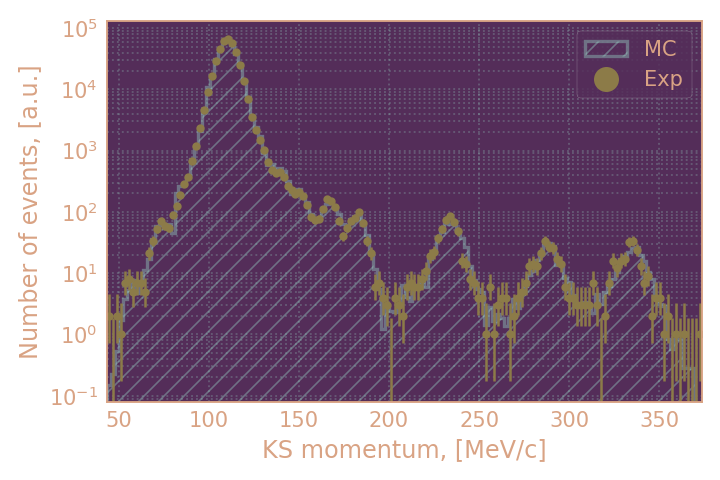 |
| Распределение отобранных событий по x1 для KS, HIGH19 | Распределение отобранных событий по x1 для KS, RHO18 |
|---|---|
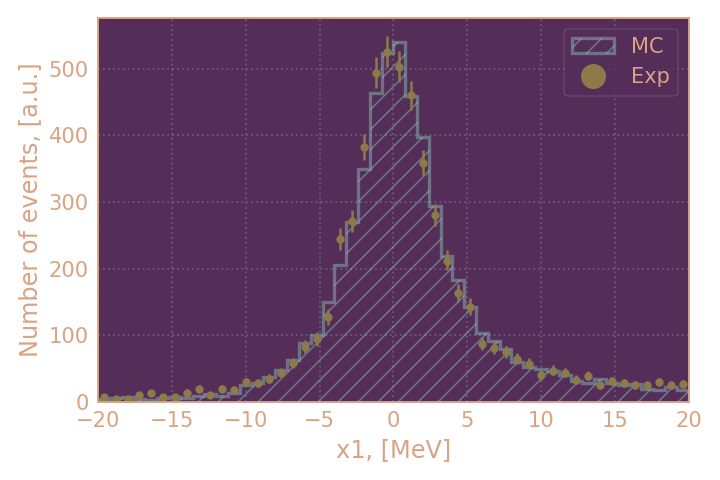 |
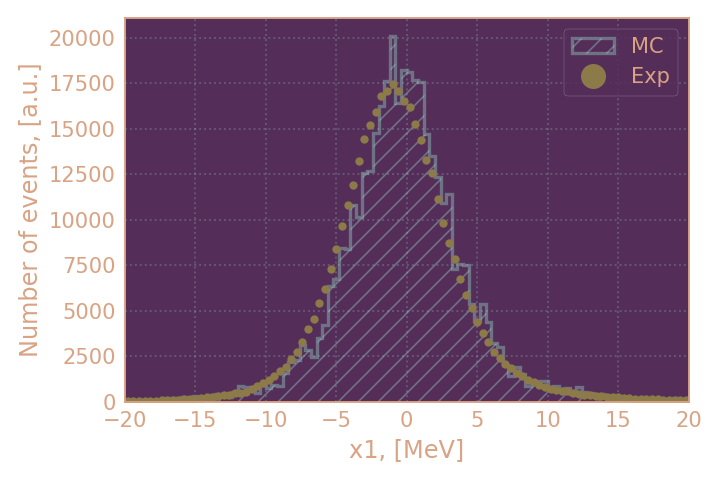 |
х1 можно считать разницей между измеренным импульсом KS и $P_0 = \sqrt{E_{beam}^2 - M_{KS}^2}$
| Распределение отобранных событий по полярному углу KS, HIGH19 | Распределение отобранных событий по полярному углу KS, RHO18 |
|---|---|
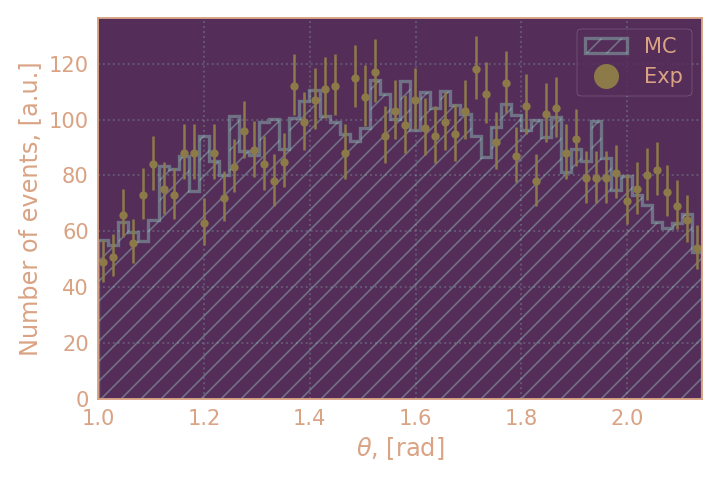 |
 |
в целом можно считать распределения согласующимися (за исключением распределения по инвариантной массе). По получившимся выборкам я буду определять эффективность KL при условии найденного KS
Поиск KL для событий с обнаруженным KS¶
| Распределение по пространственному углу (𝜓) между ближайшим кластером к обратному импульсу KS, HIGH19 | Распределение по пространственному углу (𝜓) между ближайшим кластером к обратному импульсу KS, RHO18 |
|---|---|
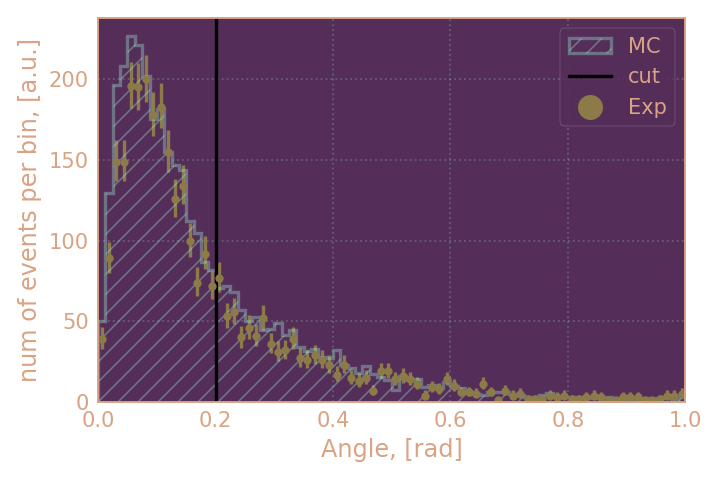 |
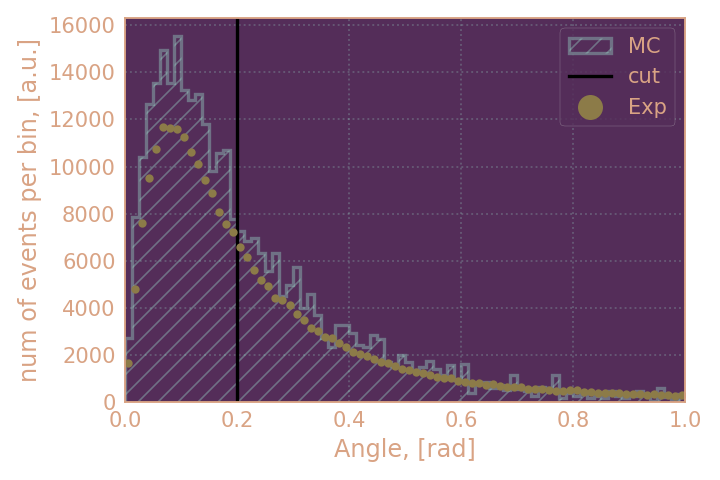 |
уже видно, что эффективность найти кластер в моделировании уже выше, чем в эксперименте, т.к. точки моделирования лежат выше
| Распределение по полному энерговыделению кандидатов в KL, HIGH19 | Распределение по полному энерговыделению кандидатов в KL, RHO18 |
|---|---|
 |
 |
| Распределение по энерговыделению в LiXe кандидатов в KL, HIGH19 | Распределение по энерговыделению в LiXe кандидатов в KL, RHO18 |
|---|---|
 |
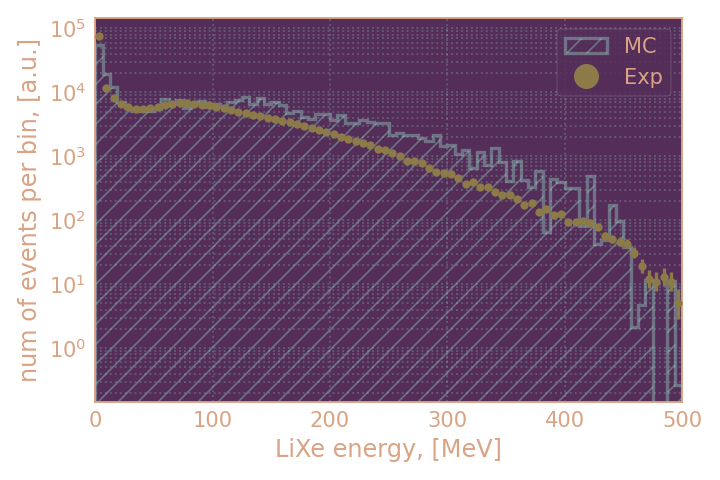 |
Визуально распределения в MC и эксперименте не согласуются
Эффективности поиска KL для событий KSKL с обнаруженным KS¶
Метод вычисления¶
сейчас эффективность вычисляется как $$\varepsilon = \frac{w_1 k_1 + ... + w_p k_p}{w_1 n_1 + ... + w_p n_p},$$ где $w_i$ - веса моделирования относительно эксперимента (для эксперимента равны 1) для каждой точки по энергии, $k_i$ - количество событий с найденным KL (из событий, где найден KS) для каждой точки по энергии, $n_i$ - количество событий, где найден KS, для каждой точки по энергии
Зависимость эффективностей от импульса KS¶
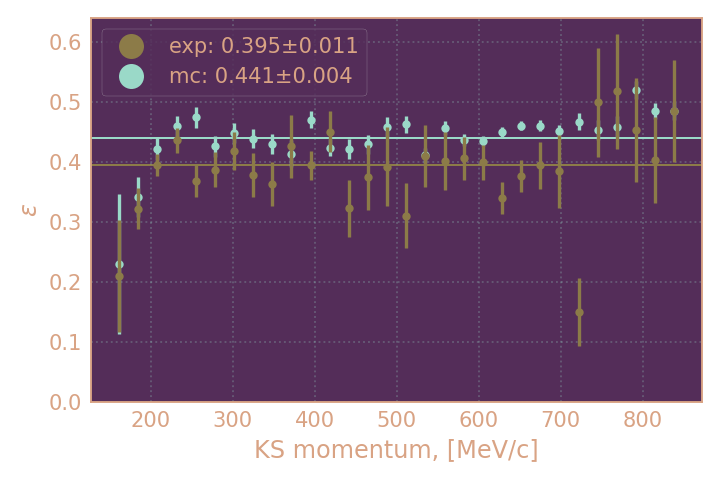
Видно значительное расхождение между MC и экспериментом. Зато числа порядка ожидаемых, ведь как и говорилось, вероятность найти KL по обнаруженному KS порядка 50%
Если KL это только кластер в пределах 0.2 рад¶
(1) На картинках ниже KL считался найденным, если был обнаружен кластер с любой энергией в пределах пространственного угла 0.2 рад. от импульса, обратного импульсу KS
| Эффективности поиска KL (1) в зависимости от импульса KS, HIGH19 | Эффективности поиска KL (1) в зависимости от импульса KS, RHO18 |
|---|---|
 |
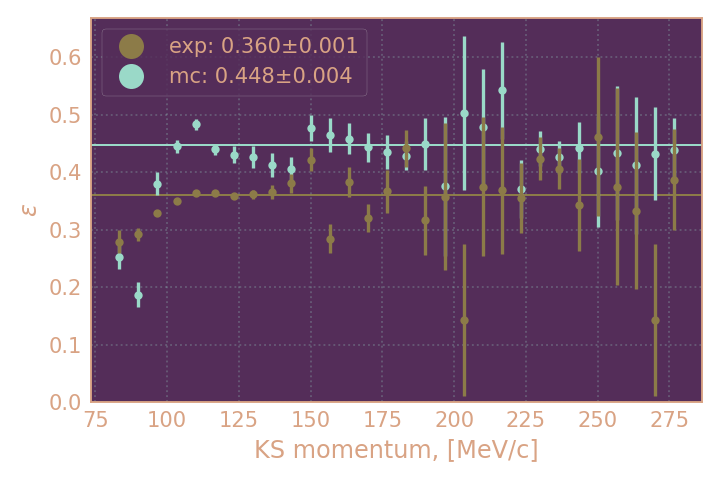 |
| линиями и в легенде обозначена усреднённая эффективность для MC и эксперимента в диапазоне от 300 до 600 МэВ/с. | линиями и в легенде обозначена усреднённая эффективность для MC и эксперимента в диапазоне от 100 до 250 МэВ/с. |
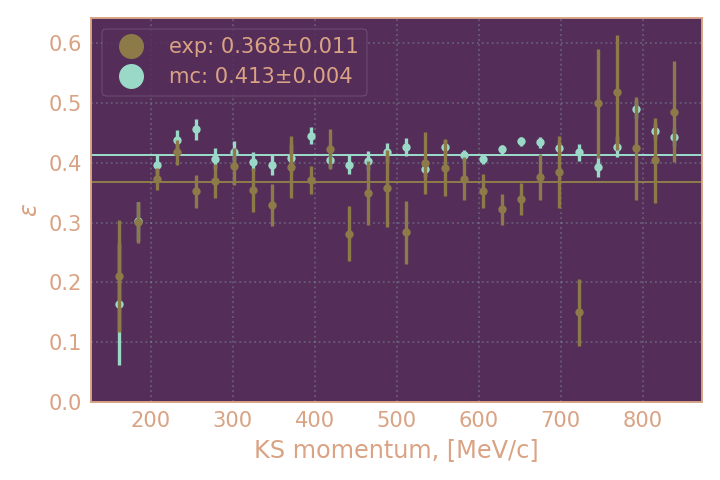
Если KL это кластер в пределах 0.2 рад + полное энерговыделение в нём > 50 МэВ¶
(2) На картинках ниже KL считался найденным, если был обнаружен кластер с любой энергией в пределах пространственного угла 0.2 рад. от импульса, обратного импульсу KS и полное энерговыделение в этом кластере было больше 50 МэВ
| Эффективности поиска KL (2) в зависимости от импульса KS, HIGH19 | Эффективности поиска KL (2) в зависимости от импульса KS, RHO18 |
|---|---|
 |
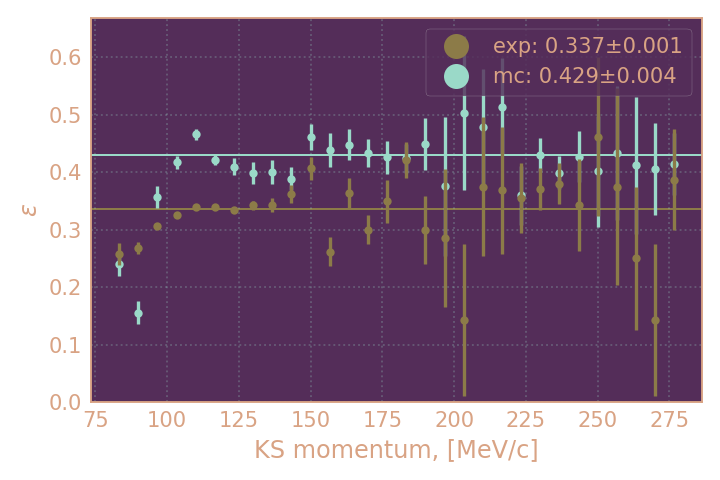 |
| линиями и в легенде обозначена усреднённая эффективность для MC и эксперимента в диапазоне от 300 до 600 МэВ/с. | линиями и в легенде обозначена усреднённая эффективность для MC и эксперимента в диапазоне от 100 до 250 МэВ/с. |
Видим ещё большее рассогласование