Problem Set 2 - Making a transit lightcurve¶

You will have two weeks to complete this problem set (and it will be worth 30 points). Solutions are due by 18:00 on Friday 29th November.

The topic of this problem set is analysis of recent Astronomical data, but the techniques used here can easily be applied to other problems. If you have any questions about the Astronomy side of things, please let me know!

Your solution should be submitted as an IPython notebook (see course introduction for instructions). If you have issues with this, please ask!

Introduction¶

Extrasolar planets (or exoplanets) are planets that have been found around other stars than the Sun. The first extrasolar planet was discovered in 1995, and since then, over 700 exoplanets have been discovered! One method to find exoplanets is to look for dips in brightness as planets pass in front of the star, as demonstrated in the following animation:

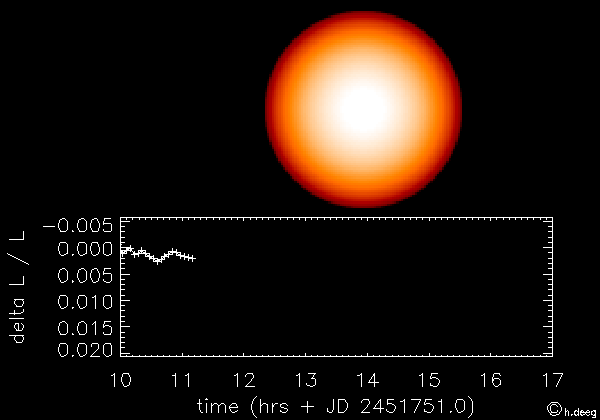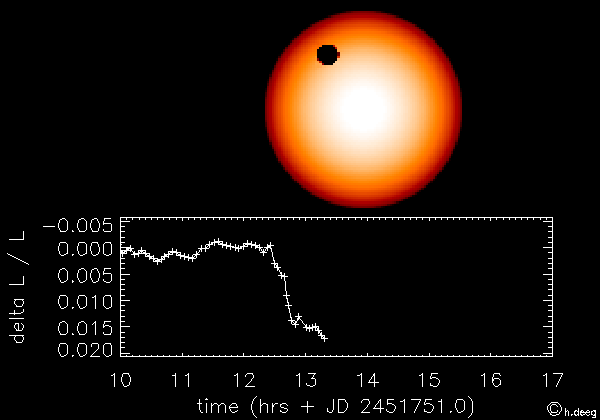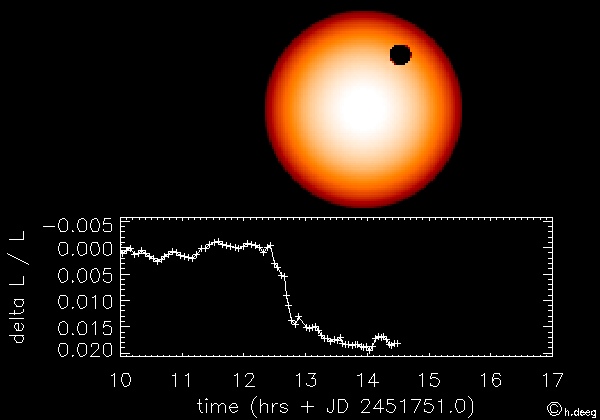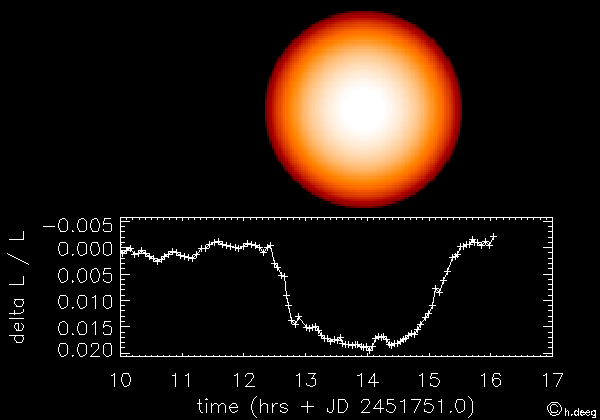
Because other stars only appear as points because they are so far away, we have to look for changes in the brightness. However, this is difficult, because planets are typically much smaller than their host star. If we were around another star, and could observe the planets in the solar system transit in front of the Sun, Jupiter would cause the Sun to become fainter by ~1%, and the Earth would cause the Sun to become fainter by ~0.01%.

Many of the recent discoveries of exoplanets by this method have been found by the Kepler spacecraft which is a telescope that was launched into space in 2009. The reason for using a space telescope is that it is much easier to accurately measure the brightness of stars without the atmosphere in the way, which makes it easier to detect smaller planets. Kepler has observed the same part of the sky many times, and several hundred planets have been discovered by this mission.

In this practical exercise, we will analyze some of the real data from Kepler for one of the stars, to look for a planet.

First, you will need to download the data and decompress it so that you have a folder called data. On Linux, you can decompress the file with:

tar xvzf kepler_data.tgz

This folder contains several different lightcurves, which give the brightness of the star against time. The first column is the time since the start of the mission, in days, and the second column is the brightness in relative units (1 is the average brightness of the star).

Part 1 - Finding the transit lightcurve from a single dataset (22 points)¶

1 - To start with, we will look at one of the lightcurves - data/kplr002571238-2009259160929_llc.txt. Read in the data from this file, and make a plot of brightness versus time to see what the data looks like. You will see that the brightness changes in an irregular way over time - this is mostly due to intrinsic changes in the brightness of the star, not the planet. However, you will see very small and narrow 'dips' that are evenly spaced - these are the planet transits!

2 - We want to get rid of the large-scale variations that are just due to the changes in brightness of the star. Write a function that given two arrays x and y and a width width will return a new array containing median-filtered values of y. Median filtering means that you create a new array y_new where y_new[i] is the median of all y[i] values between x[i] - width/2. and x[i] + width/2.. Use this function to filter the lightcurve we are currently looking at using a width of 1 day. Make a plot showing the original fluxes with black points, and the smoothed (median filtered) version as a red line on top of the points. You should see that the curve reproduces the variations in the original data, but does not include the small 'dips' due to the planet.

3 - Make a residual plot, that is a plot that shows the original data minus the smoothed version. This plot should show a mostly flat curve that includes regular dips due to the planet. Median filtering is a good way to get rid of variations in the stellar brightness that happen on longer timescales than the transit.

4 - Now try and estimate the period of the transits using the plot. The easiest way to do this is to simply draw a vertical line (for example using plt.axvline) at the position of one of the transits, and trying to plot a second line lining up with the second transit, then look at the difference between these times. You should be able to estimate the period correctly within plus or minus one day.

5 - Make a new plot of the brightness, but now instead of showing time on the x-axis, shows the phase, which is:

phase = (time % period) / period

where period is the period you determined in step 4. This basically shows how the flux of the star changes over the period of the variations, and is called a folded light-curve. If the period is correct, the transits (the dips in the lightcurve) will line up. However, it's likely that the period you found in step 4 is not perfect, so that the transits will not quite line up. Try changing the period a little either way to try and make all the transits line up, and record your value. Try and change the x-axis so that the transit happens at a phase of 0.5 (keeping the phase between 0 and 1) and make a plot of the points between a phase of 0.45 and 0.55.

6 - What you should see now is essentially a combined lightcurve of several transits! We can now start answering scientific questions. For example:

• Estimate the depth of the transit relative to the brightness of the star. The depth of the transit is how much the brightness decreases by in the middle of the transit (just estimate from the plot, no need to program this)

• How long does the transit last? (just estimate from the plot, no need to program this)

• Can you estimate the radius of the planet relative to the star?

• The star is 0.85 times the radius of the Sun. How large is the planet compared to the Earth? (try and answer these questions from your lightcurve).

• Kepler's third law states for circular orbits that the orbital period of a planet $T$ is related to the radius of the orbit $R$ by:

  $$\frac{4\pi^2}{T^2} = \frac{G\,M}{R^3}$$

  where $G$ is the gravitational constant, and M is the mass of the star. $T$ is the period you determined above, and $M$ is known to be 0.936 times the mass of the sun. What is the value of $R$?

• How does this planetary system compare to the Earth? Is it likely that there is liquid water on the planet?

Part 2 - Combining all the datasets to improve accuracy (8 points)¶

7 - Now read in all the datasets, and for each one, find the smoothed lightcurve and subtract it from the data. Then, combine the resulting datasets into a single time array and a single brightness array, and make a folded lightcurve (with phase on the x-axis) as in Step 6, showing the phase between 0 and 1. It's likely that you won't see the transit as well (or maybe not at all) since now that the datasets span a larger time range, you will need the period to be more accurate.

8 - You can either try and manually adjust the period until you get a clean folded lightcurve including all the data, or you can try and automatically determine a more accurate period. There are different ways that this can be done, so you can try and develop your own algorithm to do it. If you need any ideas, then consider for example the following algorithm, which relies on the fact that when the period is wrong, the transits are scattered around in phase, and when the period is correct, the transits are all around the same values of the phase (so the scatter in the phase values of the points in the transits is low):

• Choose a period, and compute the corresponding phase as in Step 5. Then, select all points with fluxes below a certain threshold i.e. points that show the star's brightness during the transit event (e.g. below -0.0004).

• Find the standard deviation of the phase of these points (not the brightness)

• Repeat for several different periods. I would recommend trying 100 or more values between 0.8 and 1.2 times the period you previously estimated

• Make a plot of the standard deviation versus the period, and you should see a strong dip for the best period.

• Extract the value of the phase for the lowest standard deviation

Once you have this, you can once again make a folded lightcurve of the transit, and you should now see a very nice transit lightcurve. You can now try and update your answers for Step 6.