Modèles d'influence bornée¶
Sujet d'ARE Dynamic 2018 (Maximilien Danisch, Pierre Fournier, Arthur Guillon, Jean-Daniel Kant, Baptiste Lefebvre, Nicolas Maudet)
Introduction¶
Considérons un ensemble donné d'individus que l'on appelera population. Chacun de ces individus possède une opinion, c'est-à-dire un ensemble de convictions, de valeurs, de jugements, de préjugés et de croyances qui lui sont propres. Naturellement, nous pouvons nous attendre à ce que l'opinion d'un individu donné ne soit pas constamment la même au cours du temps. Au contraire, elle évolue en fonction des rencontres faites avec d'autres individus. Lorsque la population est suffisament grande, il est impossible qu'un individu fasse connaissance avec tout le monde. Dans ce cas, ses rencontres se font avec un sous-ensemble d'individus appartenant à cette population que nous appelerons ses voisins.
Dans ce contexte, une question émerge principalement :
- Comment évolueront les opinions des individus au cours du temps ?
Pour être en mesure de proposer une réponse scientifique à cette question, nous allons chercher à modéliser cette dynamique des opinions. Autrement dit, nous allons assembler des concepts pour représenter de manière simplifiée cette dynamique en vue de la comprendre et d’en prédire certaines caractéristiques.
Pour commencer, deux questions de modélisations apparaissent immédiatement :
- Comment modéliser l'opinion d'un individu ?
- Comment modéliser le processus de mise à jour de l'opinion de cet individu ?
Dans la première partie de l'ARE, nous allons étudier un modèle en particulier : le modèle d'influence bornée. Ce modèle effectue les deux hypothèses suivantes :
- L'opinion d'un individu $ i $ est une valeur réelle (comprise entre $ 0 $ et $ 1 $ inclus), que nous noterons $ x_i $.
- La mise à jour consiste à faire évoluer l'opinion d'un individu $ i $, lorsqu'il rencontre un individu $ j $, en appliquant la formule : $ x_i \leftarrow x_i + \mu \cdot ( x_j - x_i ) $.
Où $ \mu $ est appelé le paramètre de convergence. Ce paramètre permet de contrôler la vitesse de convergence des opinions. Sa valeur est comprise entre $ 0 $ et $ 0.5 $.
Pour mieux comprendre, prenons un exemple :
def update_opinion(x, y, mu):
"""Rule to use to update the opinions."""
xpost = x + mu * (y - x)
ypost = y + mu * (x - y)
return xpost, ypost
x = 0.3
y = 0.8
mu = 0.2
xpost, ypost = update_opinion(x, y, mu)
print("xpost:", xpost)
print("ypost:", ypost)
xpost: 0.4 ypost: 0.7000000000000001
Question : Que se passe-t-il lorsque le paramètre $ \mu $ est égal à $ 0.5 $ ?
Question : Que se passe-t-il lorsqu'il est égal à $ 0 $ ?
Une hypothèse importante de notre modèle est donc que les mises à jour sont effectuées en pair-à-pair. Il s'agit d'un choix de notre part. Bien d'autres choix sont possibles ! Nous pourrions par exemple supposer qu'un individu choisisse un autre individu et adopte son opinion tel quel. Ou bien qu'il considère les opinions d'un ensemble d'autres individus (par exemple, ses amis) et adapte son opinion à la moyenne de leurs opinions.
En effectuant un de ces autres choix nous obtiendrions une variante du modèle d'influence bornée. Ces variantes pourront donner lieu à des études dans la suite de l'ARE.
Pour conclure cette introduction, quelque mots concernant ce à quoi nous pouvons nous attendre. En fin de simulation nous pourrons typiquement observer deux types de résultats :
- Un état de consensus lorsque tous les agents possèdent la même opinion.
- Un état de polarisation lorsque des opinions divergentes subsistent dans le système.
Modèle d'influence bornée¶
Question : Mais quelle est cette borne dont il est question dans le nom du modèle ?
Il s'agit en fait d'un paramètre qui permet de conditionner le changement ou non de l'opinion d'un individu. Deux individus changeront d'opinions si la différence entre leurs opinions n'est pas trop importante. Ou plus précisement si la condition suivante est vérifiée : $ | x_i - x_j | < c $. Le paramètre $ c $ est appelé le seuil et permet de borner l'influence entre les individus, d'où le nom donné au modèle.
Question : Comment modifier la fonction précédente afin de prendre en compte ce nouveau paramètre ?
def bounded_update_opinion(x, y, mu, c):
"""Rule to use to update the opinions."""
# TODO to modify.
xpost, ypost = update_opinion(x, y, mu)
return xpost, ypost
x = 0.3
y = 0.8
mu = 0.2
c = 0.1
xpost, ypost = bounded_update_opinion(x, y, mu, c)
print("xpost:", xpost)
print("ypost:", ypost)
xpost: 0.4 ypost: 0.7000000000000001
Dynamique des opinions¶
À ce stade, il reste une composante importante du modèle à préciser. Il s'agit d'une troisième question de modélisation :
- Comment modéliser les rencontres faites par un individu (i.e. quand et avec qui) ?
Le choix qui sera fait à ce sujet aura un grand impact sur la dynamique des opinions que nous observerons. Il s'agit donc d'une hypothèse importante de notre modèle.
Nous supposons ici que le temps est discret. Les rencontres ont lieu à chaque pas de temps. Plus spécifiquement, nous considérons une dynamique asynchrone : chaque paire d'individus donne lieu à une mise à jour de leurs opinions lors de leur rencontres. (Il n'y a pas de synchronisation des mises à jour entre plusieurs paires d'individus).
L'ordre des rencontres pourra être aléatoire (par exemple en tirant une paire d'agent de manière uniforme parmi toutes les paires d'agents possibles), ou déterministe et fixé à l'avance (par exemple en considérant un processus round-robin, dans ce cas chaque individu effectura une mise à jour avec tous ses voisins).
Enfin, la dynamique peut être spatialisée, au sens où les agents ne peuvent rencontrer que certains autres agents. Par exemple, dans le premier exemple que nous considérons ci-dessous, les agents sont disposés sur un cercle: chaque agent peut donc rencontrer deux voisins.
Paramètres de votre modèle¶
En résumé, en plus de la dynamique choisie (i.e. règle de mise à jour et règles de réalisations des rencontres), les paramètres importants de notre modèle sont donc :
- le nombre d'individu :
N - le paramètre de convergence :
mu - le seuil :
c
# Global parameters
nb_steps = 20
N = 5 # number of individuals
mu = 0.5 # convergence parameter
c = 0.2 # threshold
Exemple : Dynamique aléatoire spatialisée sur un cercle¶
import numpy as np
import matplotlib.pyplot as plt
Initialisation¶
Il est possible d'initialiser votre système en créant une liste avec des valeurs tirées de manière uniforme entre $ 0 $ et $ 1 $.
def init_system():
"""Initialize the opinions of the individuals."""
state = np.random.uniform(low=0.0, high=1.0, size=N)
return state
state = init_system()
print("state:", state)
state: [ 0.28516173 0.53220575 0.54801303 0.31445409 0.27386621]
print("state[0]:", state[0])
state[0]: 0.285161728465
Sélectionner aléatoirement une paire d'agent¶
Dans ce modèle on va supposer que les rencontres sont aléatoires (alternativement, on pourrait supposer qu'un agent rencontre tour à tour son voisin de droite et son voisin de gauche, par exemple)
def sample_pair_agents():
"""Sample a pair of distinct consecutive agents uniformly."""
x = np.random.choice(N)
i = x % N
j = (x + 1) % N
return i, j
print("(i, j):", sample_pair_agents())
(i, j): (4, 0)
Passer à l'état suivant¶
def next_step(state, verbose=False):
"""Simulate the transition from one state to following one."""
i, j = sample_pair_agents()
# next_state = state.copy()
state[i], state[j] = bounded_update_opinion(state[i], state[j], mu, c)
if verbose:
print("Agents", i, "and", j, "met.")
return state
print(next_step(state, verbose=True))
Agents 3 and 4 met. [ 0.28516173 0.53220575 0.54801303 0.29416015 0.29416015]
Simulation¶
Et finalement, nous itérons un certain nombre de pas.
def simulate(verbose=False):
"""Simulate multiple transitions."""
results =[]
new_state = init_system()
for i in range(nb_steps):
new_state = next_step(new_state)
if verbose:
print(i, new_state)
results.append(new_state.copy())
return results
simulate(verbose=True)
0 [ 0.56894978 0.54525414 0.54525414 0.06689983 0.3049582 ] 1 [ 0.56894978 0.54525414 0.54525414 0.18592901 0.18592901] 2 [ 0.3774394 0.54525414 0.54525414 0.18592901 0.3774394 ] 3 [ 0.46134677 0.46134677 0.54525414 0.18592901 0.3774394 ] 4 [ 0.46134677 0.50330045 0.50330045 0.18592901 0.3774394 ] 5 [ 0.46134677 0.50330045 0.34461473 0.34461473 0.3774394 ] 6 [ 0.41939308 0.50330045 0.34461473 0.34461473 0.41939308] 7 [ 0.46134677 0.46134677 0.34461473 0.34461473 0.41939308] 8 [ 0.46134677 0.40298075 0.40298075 0.34461473 0.41939308] 9 [ 0.44036993 0.40298075 0.40298075 0.34461473 0.44036993] 10 [ 0.44036993 0.40298075 0.40298075 0.34461473 0.44036993] 11 [ 0.44036993 0.40298075 0.40298075 0.34461473 0.44036993] 12 [ 0.44036993 0.40298075 0.37379774 0.37379774 0.44036993] 13 [ 0.44036993 0.38838925 0.38838925 0.37379774 0.44036993] 14 [ 0.44036993 0.38838925 0.38838925 0.37379774 0.44036993] 15 [ 0.44036993 0.38838925 0.38838925 0.37379774 0.44036993] 16 [ 0.44036993 0.38838925 0.38838925 0.37379774 0.44036993] 17 [ 0.41437959 0.41437959 0.38838925 0.37379774 0.44036993] 18 [ 0.41437959 0.40138442 0.40138442 0.37379774 0.44036993] 19 [ 0.41437959 0.40138442 0.40138442 0.37379774 0.44036993]
[array([ 0.56894978, 0.54525414, 0.54525414, 0.06689983, 0.3049582 ]), array([ 0.56894978, 0.54525414, 0.54525414, 0.18592901, 0.18592901]), array([ 0.3774394 , 0.54525414, 0.54525414, 0.18592901, 0.3774394 ]), array([ 0.46134677, 0.46134677, 0.54525414, 0.18592901, 0.3774394 ]), array([ 0.46134677, 0.50330045, 0.50330045, 0.18592901, 0.3774394 ]), array([ 0.46134677, 0.50330045, 0.34461473, 0.34461473, 0.3774394 ]), array([ 0.41939308, 0.50330045, 0.34461473, 0.34461473, 0.41939308]), array([ 0.46134677, 0.46134677, 0.34461473, 0.34461473, 0.41939308]), array([ 0.46134677, 0.40298075, 0.40298075, 0.34461473, 0.41939308]), array([ 0.44036993, 0.40298075, 0.40298075, 0.34461473, 0.44036993]), array([ 0.44036993, 0.40298075, 0.40298075, 0.34461473, 0.44036993]), array([ 0.44036993, 0.40298075, 0.40298075, 0.34461473, 0.44036993]), array([ 0.44036993, 0.40298075, 0.37379774, 0.37379774, 0.44036993]), array([ 0.44036993, 0.38838925, 0.38838925, 0.37379774, 0.44036993]), array([ 0.44036993, 0.38838925, 0.38838925, 0.37379774, 0.44036993]), array([ 0.44036993, 0.38838925, 0.38838925, 0.37379774, 0.44036993]), array([ 0.44036993, 0.38838925, 0.38838925, 0.37379774, 0.44036993]), array([ 0.41437959, 0.41437959, 0.38838925, 0.37379774, 0.44036993]), array([ 0.41437959, 0.40138442, 0.40138442, 0.37379774, 0.44036993]), array([ 0.41437959, 0.40138442, 0.40138442, 0.37379774, 0.44036993])]
Visualisation¶
Afin de visualiser la dynamique, il est possible ici de représenter la simulation sous la forme d'un nuage de points (c.f. matplotlib.pyplot.scatter).
En abscisse, nous trouvons les différents pas de temps de la simulation.
Le niveau d'opinion est représenté en ordonnée.
%matplotlib inline
results = simulate()
for i in range(nb_steps):
x = i * np.ones(N)
y = results[i]
plt.scatter(x, y, s=2, c='C0')
plt.xlabel("Iteration")
plt.ylabel("Opinion")
Variante 1 : Dynamique déterministe avec graphe complet¶
Dans le cas du cercle, la dynamique étudiée était aléatoire, et les interactions fortement restreintes.
Dans cette première variante, vous devez modifier ces deux hypothèses (en supposant que chaque agent effectue tour à tour une mise à jour avec tous les autres individus) et étudier le comportement de votre modèle en variant les autres paramètres du modèle. Plus précisément, vous pourrez considérer les variantes suivantes:
- Chaque agent (dans l'ordre) rencontre tous les autres agents (dans l'ordre).
- Un agent choisi au hasard (i.e. uniformément) rencontre tous les autres agents (dans l'ordre).
- Un agent choisi au hasard (i.e. uniformément) rencontre tous les autres agents (dans le désordre).
# TODO to complete.
Variante 2 : Dynamique aléatoire spatialisée sur une grille¶
Pour cette seconde variante, vous supposerez que les individus sont disposés sur une grille à deux dimensions. Les rencontres doivent être effectuées de manière aléatoire. Vous devrez également obtenir une visualisation graphique de l'évolution des opinions (c.f. figure ci-dessous).
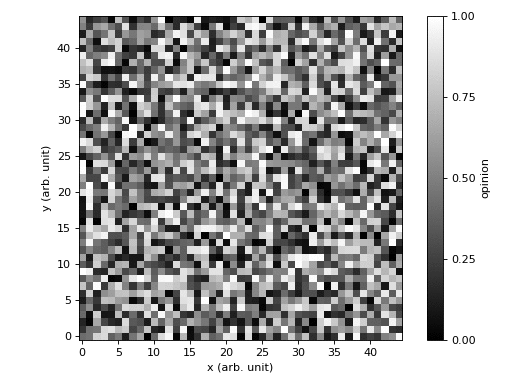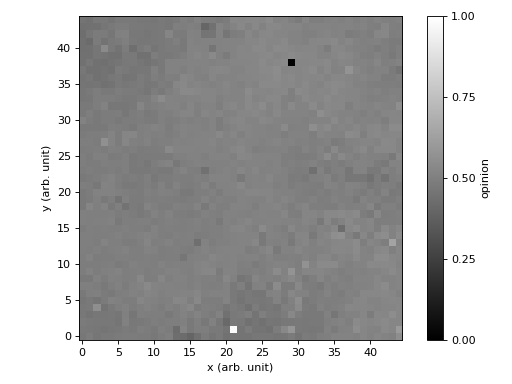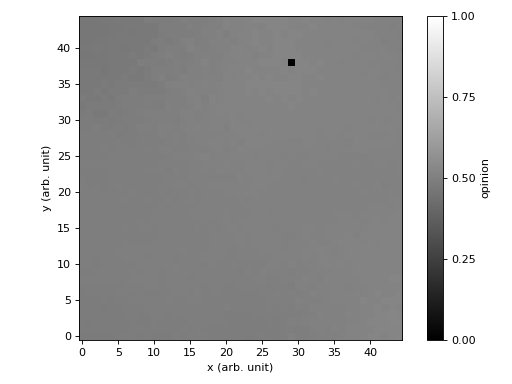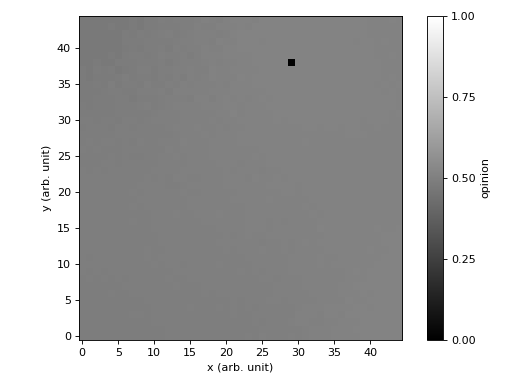
Indication : Il est recommandé d'utiliser une matrice pour représenter le système.
#TODO à compléter
<matplotlib.figure.Figure at 0x7fad2c7f8438>
Aide : Afin de visualiser la dynamique du système, on pourra utiliser sans le modifier le code suivant
fig = plt.figure()
# results[i] contient l'état au pas de temps i sous forme de matrice
im = plt.imshow(results[0], animated=True)
def updatefig(i):
im.set_array(results[i+1])
return im,
ani = animation.FuncAnimation(fig, updatefig, frames=1000, interval=50, blit=True)
HTML(ani.to_html5_video())
# Pour sauvegarder la vidéo dans un fichier externe
# ani.save('test.mp4', fps=30, extra_args=['-vcodec', 'libx264'])
Extensions¶
Idées d'extensions possibles du modèle:
- agents têtus (changent moins facilement d'avis) et/ou extrêmistes (initialisés avec une valeur 0/1)
- influence du temps sur la dynamique
...
Références¶
Le modèle d'influence bornée a été proposé par :
- Deffuant, Guillaume, et al. Mixing beliefs among interacting agents. Advances in Complex Systems 3.01n04 (2000): 87-98.
- Hegselmann, Rainer, and Ulrich Krause. Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of artificial societies and social simulation 5.3 (2002).
Dans le cas où les opinions des agents sont discrètes, en particulier binaires, on parle généralement de modèle de votant (ou voter model en anglais) (c.f.Bryan Gillespie's app).