Scipy Optimization Source ¶

SciPy optimize provides functions for minimizing (or maximizing) objective functions, possibly subject to constraints. It includes solvers for nonlinear problems (with support for both local and global optimization algorithms), linear programing, constrained and nonlinear least-squares, root finding and curve fitting.

Scalar Functions Optimization
Local (Multivariate) Optimization

    ‘Nelder-Mead’ ,‘Powell’ ,‘CG’ ,‘BFGS’ ,‘Newton-CG’ 
    ‘L-BFGS-B’  ,‘TNC’  ,‘COBYLA’  ,‘SLSQP’  ,‘trust-constr’ 
    ‘dogleg’  ,‘trust-ncg’  ,‘trust-exact’  ,‘trust-krylov’

Global Optimization
Least-squares and Curve Fitting
Root finding

Powell Method¶

Method Powell is a modification of Powell’s method [3], [4] which is a conjugate direction method. It performs sequential one-dimensional minimizations along each vector of the directions set (direc field in options and info), which is updated at each iteration of the main minimization loop. The function need not be differentiable, and no derivatives are taken. If bounds are not provided, then an unbounded line search will be used. If bounds are provided and the initial guess is within the bounds, then every function evaluation throughout the minimization procedure will be within the bounds. If bounds are provided, the initial guess is outside the bounds, and direc is full rank (default has full rank), then some function evaluations during the first iteration may be outside the bounds, but every function evaluation after the first iteration will be within the bounds. If direc is not full rank, then some parameters may not be optimized and the solution is not guaranteed to be within the bounds.

In [1]:

import numpy as np
import numpy.linalg as la
import scipy.optimize as sopt
from scipy.optimize import minimize

import matplotlib.pyplot as pt
from mpl_toolkits.mplot3d import axes3d
%matplotlib inline
import seaborn as sns
sns.set()

The minimum value of this function is 0 which is achieved when x =1

In [2]:

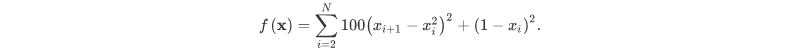
def rosen(x):
    """The Rosenbrock function"""
    return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)

In [5]:

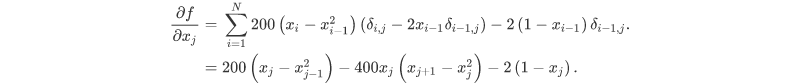
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])

In [8]:

res = minimize(rosen, x0, method='Powell',options={'xtol': 1e-8, 'disp': True})

Optimization terminated successfully.
         Current function value: 0.000000
         Iterations: 19
         Function evaluations: 1622

In [9]:

res.x

Out[9]:

array([1., 1., 1., 1., 1.])

Scipy Optimization Source¶

Powell Method¶

References¶

Scipy Optimization Source ¶