Sebastian Raschka
last updated: 05/07/2014
I am really looking forward to your comments and suggestions to improve and extend this tutorial! Just send me a quick note via Twitter: [@rasbt](https://twitter.com/rasbt) or Email: [bluewoodtree@gmail.com](mailto:bluewoodtree@gmail.com)
Kernel Density Estimation - The Parzen-window technique explained by a step-by-step approach¶
Sections¶
- 1 Introduction
- 2 Defining the Region $R_n$
- 2.1 Two different approaches - fixed volume vs. fixed number of samples in a variable volume
- 2.2 Example 3D-hypercubes
- 2.3 The window function
- 2.4 Parzen-window estimation
- 2.5 Critical parameters of the Parzen-window technique: window width and kernel
- 2.6 Critical assumption: Convergence
- 2.7 Implementing the Parzen-window estimation
- 3 Applying the Parzen-window approach to a random mutlivariate Gaussian dataset
- 3.1 Generating 10000 random 2D-patterns from a Gaussian distribution
- 3.2 Implementing and plotting the multivariate Gaussian density function
- 4 Conclusion and Drawbacks of the Parzen-window technique
- 5 Replacing the hypercube with a Gaussian Kernel
- 6 Plotting the estimates from the different Kernels
- 7 Using the kernel density estimation for a pattern classification task
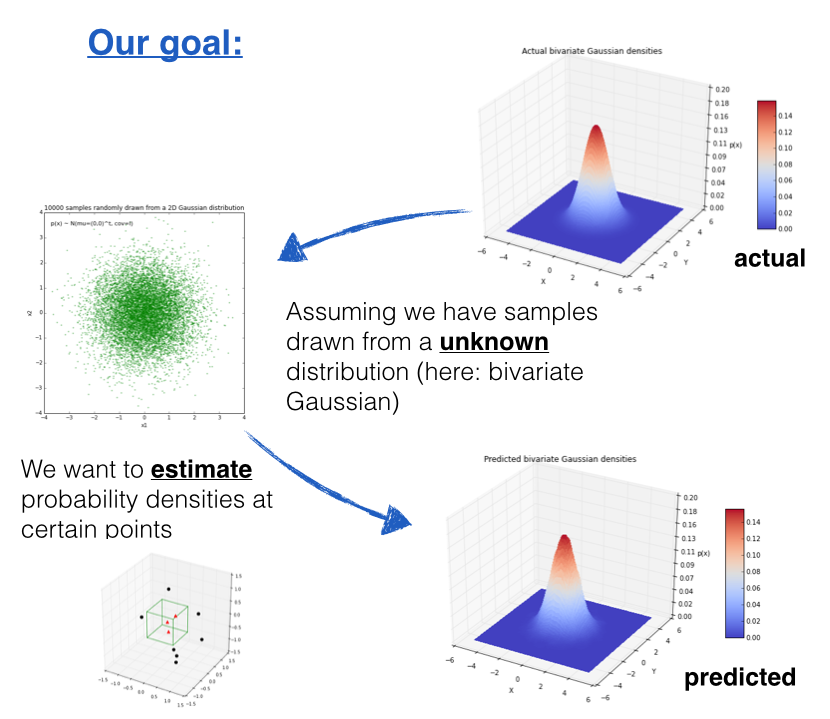
1 Introduction¶
The Parzen-window technique is a widely used non-parametric approach to estimate a probability density function $p(\pmb x)$ for a specific point $\pmb x$ from a sample $\pmb x_n$ that doesn't require any knowledge or assumption about the underying distribution.
Putting it in context - Where would this method be useful?
A popular application of the Parzen-window technique is to estimate the class-conditional densities (or also often called 'likelihoods') $p(\pmb x \; | \omega_i)$ in a supervised pattern classification problem from the training dataset (where $\pmb x$ is a multi-dimensional sample that belongs to particular class $\omega_i$).
Imagine that we are about to design a Bayes classifier for solving a statistical pattern classification task using Bayes's rule:
$P(\omega_i\; | \;\pmb x) = \frac{p(\pmb x \; | \; w_i) \cdot P(\omega_i)}{p(\pmb x)} \\ \Rightarrow posterior \; probability = \frac{\; likelihood \; \cdot \; prior \; probability}{evidence}$
If the parameters of the the class-conditional densities (also called likelihoods) are known, it is pretty easy to design the classifier. I have solved some simple examples in IPython notebooks under the section Parametric Approaches.
However, it becomes much more challenging, if we don't don't have prior knowledge about the underlying parameters that define the model of our data.
Imagine we are about to design a classifier for a pattern classification task where the parameters of the underlying sample distribution are not known. Therefore, we wouldn't need the knowledge about the whole range of the distribution; it would be sufficient to know the probability of the particular point, which we want to classify, in order to make the decision. And here we are going to see how we can estimate this probability from the training sample.
However, the only problem of this approach would be that we would seldom have exact values - if we consider the histogram of the frequencies for a arbitrary training dataset. Therefore, we define a certain region (i.e., the Parzen-window) around the particular value to make the estimate.
And where does this name Parzen-window come from?
As it was quite common in the earlier days, this technique was named after its inventor, Emanuel Parzen, who published his detailed mathematical analysis in 1962 in the Annals of Mathematical Statistics: On the Estimation of a Probability Density Function and Mode.
2 Defining the Region $R_n$¶
The basis of this approach is to count how many samples fall within a specified region $R_n$ (or "window" if you will). Our intuition tells us, that (based on the observation), the probability that one sample falls into this region is
$p(x) = \frac{\#\;of\;samples\;in\;R}{total \; samples}$
To tackle this problem from a more mathematical standpoint to estimate "the probability of observing $k$ points out of $n$ in a Region $R$" we consider a binomial distribution
$p_k = \bigg[ \begin{array}{c} n \\ k \end{array}\bigg] \cdot p^k \cdot (1-p)^{n-k}$
and make the assumption that in a binomial distribution, the probability peaks sharply at the mean, so that:
$E[k] = n \cdot p \; \sim \; k = n \cdot p$
And if we think of the probability of a continous variable, we know that it is defined as:
$p(\pmb x) = \int_R dx = p(\pmb x) \cdot V$,
where $V$ is the volume of the region $R$,
and if we rearrange those terms, so that we arrive at the following equation, which we will use later:
$\frac{k}{n} = p(\pmb x) \cdot V \\ \Rightarrow p(\pmb x) = \frac{k / n}{V}$
This simple equation above (i.e, the "probability estimate") lets us caclulate the probability density of a point $\pmb x$ by counting how many points $k$ fall in a defined region (or volume).
2.1 Two different approaches - fixed volume vs. fixed number of samples in a variable volume¶
Now, there are two possible approaches to estimate the densities at different points $\pmb x^*$.
Case 1 - fixed volume:¶
For a particular number $n$ (= number of total points), we use volume $V$ of a fixed size and observe how many points $k$ fall into the region. In other words, we use the same volume to make an estimate at different regions.
The Parzen-window technique falls into this category!
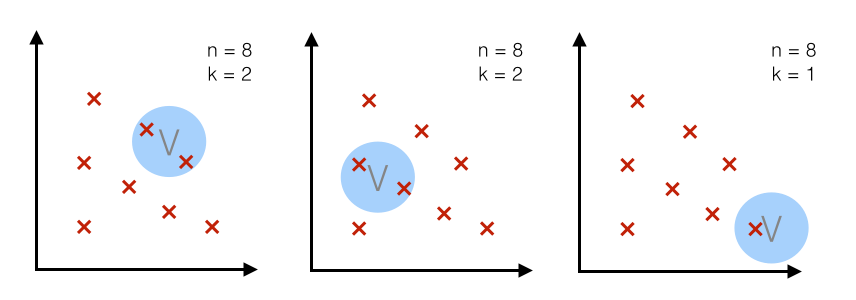
Case 2 - fixed $k$:¶
For a particular number $n$ (= number of total points), we use a fixed number $k$ (number of points that fall inside the region or volume) and adjust the volume accordingly.
(The k-nearest neighbor technique uses this approach, which will be discussed in a separate article.)
2.2 Example 3D-hypercubes¶
To illustrate this with an example and a set of equations, let us assume this region $R_n$ is a hypercube.
And the volume of this hypercube is defined by $V_n = {h_n}^d$, where $h_n$ is the length of the hypercube, and $d$ is the number of dimensions.
For an 2D-hypercube with length 1, for example, this would be $V_1 = {1}^2$ and for a 3D hypercube $V_1 = {1}^3$, respectively.
So let us visualize such an simple example: a typical 3-dimensional unit hypercube ($h_1 = 1$) representing the region $R_1$, and 10 sample points, where 3 of them lie within the hypercube (red triangles), and the other 7 outside (blue dots).
Note that using a hypercube would not be an ideal choice for a real application, but it certainly makes the implementations of the following steps a lot shorter and easier to follow.
%pylab inline
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from itertools import product, combinations
fig = plt.figure(figsize=(7,7))
ax = fig.gca(projection='3d')
ax.set_aspect("equal")
# Plot Points
# samples within the cube
X_inside = np.array([[0,0,0],[0.2,0.2,0.2],[0.1, -0.1, -0.3]])
X_outside = np.array([[-1.2,0.3,-0.3],[0.8,-0.82,-0.9],[1, 0.6, -0.7],
[0.8,0.7,0.2],[0.7,-0.8,-0.45],[-0.3, 0.6, 0.9],
[0.7,-0.6,-0.8]])
for row in X_inside:
ax.scatter(row[0], row[1], row[2], color="r", s=50, marker='^')
for row in X_outside:
ax.scatter(row[0], row[1], row[2], color="k", s=50)
# Plot Cube
h = [-0.5, 0.5]
for s, e in combinations(np.array(list(product(h,h,h))), 2):
if np.sum(np.abs(s-e)) == h[1]-h[0]:
ax.plot3D(*zip(s,e), color="g")
ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.set_zlim(-1.5, 1.5)
plt.show()
Populating the interactive namespace from numpy and matplotlib
2.3 The window function¶
Once we visualized the region $R_1$ like above, it is easy and intuitive to count how many samples fall within this region, and how many lie outside. To approach this problem more mathematically, we would use the following equation to count the samples $k_n$ within this hypercube, where $\phi$ is our so-called window function:
$\phi(\pmb u) = \Bigg[ \begin{array}{ll} 1 & \quad |u_j| \leq 1/2 \; ;\quad \quad j = 1, ..., d \\
0 & \quad otherwise \end{array} $
for a hypercube of unit length 1 centered at the coordinate system's origin. What this function basically does is assigning a value 1 to a sample point if it lies within 1/2 of the edges of the hypercube, and 0 if lies outside (note that the evaluation is done for all dimensions of the sample point).
If we extend on this concept, we can define a more general equation that applies to hypercubes of any length $h_n$ that are centered at $\pmb x$:
$k_n = \sum\limits_{i=1}^{n} \phi \bigg( \frac{\pmb x - \pmb x_i}{h_n} \bigg)$
where $\pmb u = \bigg( \frac{\pmb x - \pmb x_i}{h_n} \bigg)$
2.3.1 Implementing the window function¶
def window_function(x_vec, unit_len=1):
"""
Implementation of the window function. Returns 1 if 3x1-sample vector
lies within a origin-centered hypercube, 0 otherwise.
"""
for row in x_vec:
if np.abs(row) > (unit_len/2):
return 0
return 1
2.3.2 Quantifying the sample points inside and outside $R_n$ (the 3D-hypercube)¶
Using the window function that we just implemented above, let us now quantify how many points actually lie inside and outside the hypercube.
X_all = np.vstack((X_inside,X_outside))
assert(X_all.shape == (10,3))
k_n = 0
for row in X_all:
k_n += window_function(row.reshape(3,1))
print('Points inside the hypercube:', k_n)
print('Points outside the hybercube:', len(X_all) - k_n)
Points inside the hypercube: 3 Points outside the hybercube: 7
2.4 Parzen-window estimation¶
Based on the window function that we defined in the section above, we can now formulate the Parzen-window estimation with a hypercube kernel as follows:
$p_n(\pmb x) = \frac{1}{n} \sum\limits_{i=1}^{n} \frac{1}{h^d} \phi \bigg[ \frac{\pmb x - \pmb x_i}{h_n} \bigg]$
where
$h^d = V_n\quad$ and $\quad\phi \bigg[ \frac{\pmb x - \pmb x_i}{h_n} \bigg] = k$
And applying this to out unit-hypercube example above, for which 3 out of 10 samples fall inside the hypercube (region $R$), we can calculate the probability $p(\pmb x)$ that $\pmb x$ samples fall within region $R$ as follows:
$p(\pmb x) = \frac{k/n}{h^d} = \frac{3/10}{1^3} = \frac{3}{10} = 0.3$
2.6 Critical assumption: Convergence¶
One of the most critical assumptions why this technique works (i.e., the Parzen-window estimation, but the k-nearest neighbor technique as well), is that $p_n$ (where $n$ stands for the "number of samples", not "non-parametric" ;) ) converges to the true density $p(\pmb x)$ when we assume an infinite number of training samples, which was nicely shown by Emanuel Parzen in his paper.
2.5 Critical parameters of the Parzen-window technique: window width and kernel¶
The two critical parameters in the Parzen-window techniques are
- the window width
- the kernel
1) window width:¶
Let us skip this part for now and discuss and explore the question of choosing an appropriate window width laterby using an hands-on example.
2) kernel:¶
Most commonly, either a hypercube or a Gaussian kernel is used for the window function. But how do we know which is better? It really depends on the training sample. In practice, the choice is often made by testing the derived pattern classifier to see which method leads to a better performance on the test data set.
Intuitively, it would make sense to use a Gaussian kernel for a data set that follows a Gaussian distribution. But remmeber, the whole purpose of the Parzen-window estimation is to estimate densities of a unknown distribution! So, in practice we wouldn't know whether our data stems from a Gaussian distribution or not (otherwise we wouldn't need to estimate, but can use a parametric techniqe like MLE or Bayesian Estimation).
If we would decide to use a Gaussian kernel instead of the hypercube, we can just simply swap the terms of the window function, which we defined above for the hypercube, by:
$\frac{1}{(\sqrt{2 \pi})^d h_{n}^{d}} exp \; \bigg[ -\frac{1}{2} \bigg(\frac{\pmb x - \pmb x_i}{h_n} \bigg)^2 \bigg]$
The Parzen-window estimation would then look like this:
$p_n(\pmb x) = \frac{1}{n} \sum\limits_{i=1}^{n} \frac{1}{h^d} \phi \Bigg[ \frac{1}{(\sqrt {2 \pi})^d h_{n}^{d}} exp \; \bigg[ -\frac{1}{2} \bigg(\frac{\pmb x - \pmb x_i}{h_n} \bigg)^2 \bigg] \Bigg]$
**mixing different kernels:** In some papers you will see, that the authors mixed hypercube and Gaussian kernels to estimate the densities at different regions. In practice, this might work very well, however, but note that in theory this would violate on of the underlying principles: that the density integrates to 1.
$\lim\limits_{n \rightarrow \infty}{p_n(\pmb x)} = p(\pmb x)$
A few other requirements are that at the limit the volume we choose for the Parzen-window becomes infinite small:
$\lim\limits_{n \rightarrow \infty}{V_n} = 0$
and the number of points $k_n$ in this region converges to:
$\lim\limits_{n \rightarrow \infty}{k_n} = \infty$
from which we can conclude:
$\lim\limits_{n \rightarrow \infty}{\frac{k_n}{n}} = 0$
2.7 Implementing the Parzen-window estimation¶
And again, let us go to the more interesting part and implement the code for the hypercube kernel:
def parzen_window_est(x_samples, h=1, center=[0,0,0]):
'''
Implementation of the Parzen-window estimation for hypercubes.
Keyword arguments:
x_samples: A 'n x d'-dimensional numpy array, where each sample
is stored in a separate row.
h: The length of the hypercube.
center: The coordinate center of the hypercube
Returns the probability density for observing k samples inside the hypercube.
'''
dimensions = x_samples.shape[1]
assert (len(center) == dimensions), 'Number of center coordinates have to match sample dimensions'
k = 0
for x in x_samples:
is_inside = 1
for axis,center_point in zip(x, center):
if np.abs(axis-center_point) > (h/2):
is_inside = 0
k += is_inside
return (k / len(x_samples)) / (h**dimensions)
print('p(x) =', parzen_window_est(X_all, h=1))
p(x) = 0.3
At this point I can fully understand if you lost the overview a little bit. I summarized the three crucial parts (hypercube kernel, window function, and the resulting parzen-window estimation) in a later section, and I think it is worthwhile to take a brief look at it, before we apply it to a data set below.
3 Applying the Parzen-window approach to a random mutlivariate Gaussian dataset¶
Let us use an 2-dimensional dataset drawn from a multivariate Gaussian distribution to apply the Parzen-window technique for the density estimation.
3.1 Generating 10000 random 2D-patterns from a Gaussian distribution]¶
The general multivariate Gaussian probability density function (pdf) is defined as:
$p(\pmb x) = \frac{1}{(2\pi)^{d/2} \; |\Sigma|^{1/2}} exp \bigg[ -\frac{1}{2}(\pmb x - \pmb \mu)^t \Sigma^{-1}(\pmb x - \pmb \mu) \bigg]$
And we will use the following parameters for drawing the random samples:
$\pmb{\mu} = \bigg[
\begin{array}{c}
0\\
0\\
\end{array} \bigg]\;, \quad$
$\Sigma = \bigg[
\begin{array}{cc}
\sigma_{11}^2 & \sigma_{12}^2\\
\sigma_{21}^2 & \sigma_{22}^2\\
\end{array} \bigg] \; = \bigg[
\begin{array}{cc}
1 & 0\\
0 & 1\\
\end{array} \bigg]$
import numpy as np
# Generate 10000 random 2D-patterns
mu_vec = np.array([0,0])
cov_mat = np.array([[1,0],[0,1]])
x_2Dgauss = np.random.multivariate_normal(mu_vec, cov_mat, 10000)
print(x_2Dgauss.shape)
(10000, 2)
#%pylab inline
#from matplotlib import pyplot as plt
f, ax = plt.subplots(figsize=(7, 7))
ax.scatter(x_2Dgauss[:,0], x_2Dgauss[:,1], marker='o', color='green', s=4, alpha=0.3)
plt.title('10000 samples randomly drawn from a 2D Gaussian distribution')
plt.ylabel('x2')
plt.xlabel('x1')
ftext = 'p(x) ~ N(mu=(0,0)^t, cov=I)'
plt.figtext(.15,.85, ftext, fontsize=11, ha='left')
plt.ylim([-4,4])
plt.xlim([-4,4])
plt.show()
3.2 Implementing and plotting the multivariate Gaussian density function¶
3.2.1 Plotting the bivariate Gaussian densities¶
First, let us plot the multivariate Gaussian distribution (here: bivariate) in a 3D plot to get an better idea of the actual density distribution.
#%pylab inline
#import numpy as np
#from matplotlib import pyplot as plt
from matplotlib.mlab import bivariate_normal
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10, 7))
ax = fig.gca(projection='3d')
x = np.linspace(-5, 5, 200)
y = x
X,Y = np.meshgrid(x, y)
Z = bivariate_normal(X, Y)
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.coolwarm,
linewidth=0, antialiased=False)
ax.set_zlim(0, 0.2)
ax.zaxis.set_major_locator(plt.LinearLocator(10))
ax.zaxis.set_major_formatter(plt.FormatStrFormatter('%.02f'))
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('p(x)')
plt.title('Bivariate Gaussian distribution')
fig.colorbar(surf, shrink=0.5, aspect=7, cmap=plt.cm.coolwarm)
plt.show()
3.2.2 Implementing the code to calculate the multivariate Gaussian densities¶
To calculate the probabilities from the multivariate Gaussian density function and compare the results our estimate, let us implement it using the following equation:
$p(\pmb x) = \frac{1}{(2\pi)^{d/2} \; |\Sigma|^{1/2}} exp \bigg[ -\frac{1}{2}(\pmb x - \pmb \mu)^t \Sigma^{-1}(\pmb x - \pmb \mu) \bigg]$
Unfortunately, there is currently no Python library that provides this functionality. Good news is, that scipy.stats.multivariate_normal.pdf() will be implemented in the new release candidate of scipy (v. 0.14).
#import numpy as np
def pdf_multivariate_gauss(x, mu, cov):
'''
Caculate the multivariate normal density (pdf)
Keyword arguments:
x = numpy array of a "d x 1" sample vector
mu = numpy array of a "d x 1" mean vector
cov = "numpy array of a d x d" covariance matrix
'''
assert(mu.shape[0] > mu.shape[1]), 'mu must be a row vector'
assert(x.shape[0] > x.shape[1]), 'x must be a row vector'
assert(cov.shape[0] == cov.shape[1]), 'covariance matrix must be square'
assert(mu.shape[0] == cov.shape[0]), 'cov_mat and mu_vec must have the same dimensions'
assert(mu.shape[0] == x.shape[0]), 'mu and x must have the same dimensions'
part1 = 1 / ( ((2* np.pi)**(len(mu)/2)) * (np.linalg.det(cov)**(1/2)) )
part2 = (-1/2) * ((x-mu).T.dot(np.linalg.inv(cov))).dot((x-mu))
return float(part1 * np.exp(part2))
3.2.2.1 Testing the multivariate Gaussian PDF implementation¶
Let us quickly confirm that the multivariate Gaussian, which we just implemented, works as expected by comparing
it with the bivariate Gaussian from the matplotlib.mlab package.
from matplotlib.mlab import bivariate_normal
x = np.array([[0],[0]])
mu = np.array([[0],[0]])
cov = np.eye(2)
mlab_gauss = bivariate_normal(x,x)
mlab_gauss = float(mlab_gauss[0]) # because mlab returns an np.array
impl_gauss = pdf_multivariate_gauss(x, mu, cov)
print('mlab_gauss:', mlab_gauss)
print('impl_gauss:', impl_gauss)
assert(mlab_gauss == impl_gauss), 'Implementations of the mult. Gaussian return different pdfs'
mlab_gauss: 0.15915494309189535 impl_gauss: 0.15915494309189535
3.2.3 Comparing the Parzen-window estimation to the actual densities¶
And finally, let us compare the densities that we estimate using our implementation of the Parzen-window estimation with the actual multivariate Gaussian densities.
But before we do the comparison, we have to ask ourselves one more question: Which window size should we choose (i.e., what should be the side length $h$ of our hypercube)?
The window width is a function of the number of training samples,
$h_n \propto \frac{1}{\sqrt{n}}$
But why $\sqrt{n}$, not just $n$?
This is because the number of $k_n$ points within a window grows much smaller than the number of training samples, although
$\lim\limits_{n \rightarrow \infty}{k_n} = \infty$
we have: $ k < n$
This is also one of the biggest drawbacks of the Parzen-window technique, since in practice, the number of training data is usually (too) small, which makes the choice of an 'optimal' window size difficult.
In practice, one would choose different window widths and analyze which one results in the best performance of the derived classifier. The only guideline we have is that we assume that 'optimal' the window width shrinks with the number of training samples.
If we would choose a window width that is "too small", this would result in local spikes, and a window width that is "too big" would average over the whole distribution. Below, I try to illustrate it using a 1D-sample.
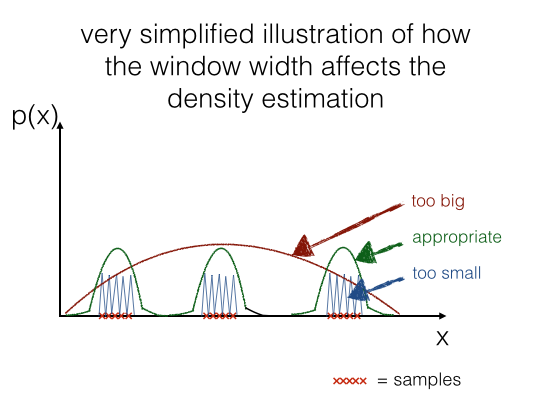
In a later section we will have a look how it looks like real data:
3.2.3.1 Choosing an appropriate window size¶
For our example, we have the luxury of knowing the distribution of our data, so let us look at some possible window widths to see how it affects the density estimation for the center of the distribution
(based on our test in the section above, we would expect a value close to $p(\pmb x) = 0.1592\;$ ).
print('Predict p(x) at the center [0,0]: ')
print('h = 0.1 ---> p(x) =', parzen_window_est(x_2Dgauss, h=0.1, center=[0, 0]))
print('h = 0.3 ---> p(x) =',parzen_window_est(x_2Dgauss, h=0.3, center=[0, 0]))
print('h = 0.6 ---> p(x) =',parzen_window_est(x_2Dgauss, h=0.6, center=[0, 0]))
print('h = 1 ---> p(x) =',parzen_window_est(x_2Dgauss, h=1, center=[0, 0]))
Predict p(x) at the center [0,0]: h = 0.1 ---> p(x) = 0.17999999999999997 h = 0.3 ---> p(x) = 0.1766666666666667 h = 0.6 ---> p(x) = 0.15694444444444444 h = 1 ---> p(x) = 0.1475
This rough estimate above gives us some idea about a window size that would give us a quite reasonable estimate: A good value for $h$ should be somewhere around 0.6.
But we can do better (maybe I should use a minimization algorithm here, but I think this example should illustrate the procedure sufficiently). So let us create 400 evenly spaced values between (0,1) for $h$ and see which gives us the estimate for the probability at the center of the distribution.
import operator
# generate a range of 400 window widths between 0 < h < 1
h_range = np.linspace(0.001, 1, 400)
# calculate the actual density at the center [0, 0]
mu = np.array([[0],[0]])
cov = np.eye(2)
actual_pdf_val = pdf_multivariate_gauss(np.array([[0],[0]]), mu, cov)
# get a list of the differnces (|estimate-actual|) for different window widths
parzen_estimates = [np.abs(parzen_window_est(x_2Dgauss, h=i, center=[0, 0])
- actual_pdf_val) for i in h_range]
# get the window width for which |estimate-actual| is closest to 0
min_index, min_value = min(enumerate(parzen_estimates), key=operator.itemgetter(1))
print('Optimal window width for this data set: ', h_range[min_index])
Optimal window width for this data set: 0.554330827068
3.2.3.2 Estimated vs. actual densities¶
Now, that we have a "appropriate" window width, let us compare the estimates to the actual densities for some example points.
import prettytable
p1 = parzen_window_est(x_2Dgauss, h=h_range[min_index], center=[0, 0])
p2 = parzen_window_est(x_2Dgauss, h=h_range[min_index], center=[0.5, 0.5])
p3 = parzen_window_est(x_2Dgauss, h=h_range[min_index], center=[0.3, 0.2])
mu = np.array([[0],[0]])
cov = np.eye(2)
a1 = pdf_multivariate_gauss(np.array([[0],[0]]), mu, cov)
a2 = pdf_multivariate_gauss(np.array([[0.5],[0.5]]), mu, cov)
a3 = pdf_multivariate_gauss(np.array([[0.3],[0.2]]), mu, cov)
results = prettytable.PrettyTable(["", "predicted", "actual"])
results.add_row(["p([0,0]^t",p1, a1])
results.add_row(["p([0.5,0.5]^t",p2, a2])
results.add_row(["p([0.3,0.2]^t",p3, a3])
print(results)
+---------------+----------------+---------------------+ | | predicted | actual | +---------------+----------------+---------------------+ | p([0,0]^t | 0.159151557695 | 0.15915494309189535 | | p([0.5,0.5]^t | 0.122208992134 | 0.12394999430965298 | | p([0.3,0.2]^t | 0.150755520068 | 0.14913891880709737 | +---------------+----------------+---------------------+
As we can see in the table above, our prediction works quite well!
3.2.3.3 Plotting the estimated bivariate Gaussian densities¶
Last but not least, let us plot the densities that we'd predict using the Parzen-window technique with a hypercube!
%pylab inline
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
##############################################
### Predicted bivariate Gaussian densities ###
##############################################
fig = plt.figure(figsize=(10, 7))
ax = fig.gca(projection='3d')
X = np.linspace(-5, 5, 100)
Y = np.linspace(-5, 5, 100)
X,Y = np.meshgrid(X,Y)
Z = []
for i,j in zip(X.ravel(),Y.ravel()):
Z.append(parzen_window_est(x_2Dgauss, h=h_range[min_index], center=[i, j]))
Z = np.asarray(Z).reshape(100,100)
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.coolwarm,
linewidth=0, antialiased=False)
ax.set_zlim(0, 0.2)
ax.zaxis.set_major_locator(plt.LinearLocator(10))
ax.zaxis.set_major_formatter(plt.FormatStrFormatter('%.02f'))
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('p(x)')
plt.title('Predicted bivariate Gaussian densities')
fig.colorbar(surf, shrink=0.5, aspect=7, cmap=plt.cm.coolwarm)
###########################################
### Actual bivariate Gaussian densities ###
###########################################
fig = plt.figure(figsize=(10, 7))
ax = fig.gca(projection='3d')
x = np.linspace(-5, 5, 100)
y = x
X,Y = np.meshgrid(x, y)
Z = bivariate_normal(X, Y)
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.coolwarm,
linewidth=0, antialiased=False)
ax.set_zlim(0, 0.2)
ax.zaxis.set_major_locator(plt.LinearLocator(10))
ax.zaxis.set_major_formatter(plt.FormatStrFormatter('%.02f'))
fig.colorbar(surf, shrink=0.5, aspect=7, cmap=plt.cm.coolwarm)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('p(x)')
plt.title('Actual bivariate Gaussian densities')
plt.show()