from IPython.display import Image
from IPython.core.display import HTML
Example 1¶
Consider the flow of a fluid $A$ that has the following density $\rho$, and a viscosity $\mu$ down a pipe of diamtere $D$ and surface roughness $e$ at a mean flow velocity $V$
Image(url= "https://www.lmnoeng.com/Pressure/Pressure_Drop_dwg.jpg")
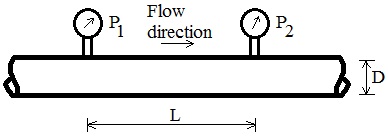
We are measuring the pressure drop in the pipe between two different position $\Delta p = p_2 - p_1$ separated by a distance $L$. $$\Delta p_L = f(V, D, \rho, \mu, L, e)$$
Using Buckingham Pi theorem we can reduce the dimensionality of the problem $$f(V, D, \rho, \mu, L, e) \implies f(\pi_1, \pi_2, \cdots)$$ where $\pi_i$ are dimensionless parameters constructed from the original variables.
from src.buckinghampi import BuckinghamPi
pipe_flow = BuckinghamPi(physical_dimensions='m l t')
pipe_flow.add_variable(name='dp',expression='m/(l*t**2)')
pipe_flow.add_variable(name='V',expression='l/t')
pipe_flow.add_variable(name='D',expression='l')
pipe_flow.add_variable(name='rho',expression='m/(l**3)')
pipe_flow.add_variable(name='L',expression='l')
pipe_flow.add_variable(name='mu',expression='m/(l*t)')
pipe_flow.add_variable(name='e',expression='l')
pipe_flow.generate_pi_terms()
for piterms in pipe_flow.pi_terms:
print('-----------------')
for term in piterms:
print(term)
100%|██████████| 5040/5040 [00:12<00:00, 411.17it/s]
----------------- L/e D/e V*e*rho/mu dp*e**2*rho/mu**2 ----------------- e/L L**2*dp*rho/mu**2 D/L L*V*rho/mu ----------------- L/e D/e mu/(V*e*rho) dp/(V**2*rho) ----------------- e/L D/L mu/(L*sqrt(dp)*sqrt(rho)) V*sqrt(rho)/sqrt(dp) ----------------- L/e D/e mu/(sqrt(dp)*e*sqrt(rho)) V*sqrt(rho)/sqrt(dp) ----------------- e/L dp/(V**2*rho) mu/(L*V*rho) D/L ----------------- L/e D/e V*e*rho/mu dp*e/(V*mu) ----------------- e/L D/L L**2*dp*rho/mu**2 V*mu/(L*dp) ----------------- D/L e/L L*dp/(V*mu) L*V*rho/mu ----------------- e/D L/D D**2*dp*rho/mu**2 V*mu/(D*dp) ----------------- e/D L/D D*dp/(V*mu) D*V*rho/mu ----------------- e/D L/D mu/(D*sqrt(dp)*sqrt(rho)) V*sqrt(rho)/sqrt(dp) ----------------- D/L e/L V*mu/(L*dp) V**2*rho/dp ----------------- L/D e/D V*mu/(D*dp) V**2*rho/dp ----------------- D*V*rho/mu e/D D**2*dp*rho/mu**2 L/D ----------------- dp/(V**2*rho) e/D mu/(D*V*rho) L/D ----------------- V*mu/(dp*e) L/e V**2*rho/dp D/e ----------------- dp*e/(V*mu) L*dp/(V*mu) D*dp/(V*mu) V**2*rho/dp ----------------- D*V*rho/mu V*e*rho/mu dp/(V**2*rho) L*V*rho/mu ----------------- L/e dp*e**2*rho/mu**2 D/e V*mu/(dp*e) ----------------- D*sqrt(dp)*sqrt(rho)/mu sqrt(dp)*e*sqrt(rho)/mu V*sqrt(rho)/sqrt(dp) L*sqrt(dp)*sqrt(rho)/mu
Example 2¶
The stability of a numerical time integrator in a fluid flow simulation for an incompressible flow on a staggered uniform grid is hinged upon the following set of variables:
- Advection velocity: $u \rightarrow \frac{L}{T}$
- Density of the fluid: $\rho \rightarrow \frac{M}{L**3}$
- Dynamic viscosity: $\mu \rightarrow \frac{M}{LT}$
- Grid spacing: $\mathrm{d}x \rightarrow L$
- Time step: $\mathrm{d}t \rightarrow T$
using the Buckingham Pi module we can obtain the dimensionless $\pi$ terms that describe this example
stability = BuckinghamPi('M L T')
stability.add_variable('u','L/T')
stability.add_variable('rho','M/(L**3)')
stability.add_variable('mu','M/(L*T)')
stability.add_variable('dx','L')
stability.add_variable('dt','T')
stability.generate_pi_terms()
for piterms in stability.pi_terms:
print('-----------------')
for term in piterms:
print(term)
100%|██████████| 120/120 [00:00<00:00, 617.75it/s]
----------------- dx**2*rho/(dt*mu) dt*u/dx ----------------- dx*sqrt(rho)/(sqrt(dt)*sqrt(mu)) sqrt(dt)*sqrt(rho)*u/sqrt(mu) ----------------- dx/(dt*u) dt*rho*u**2/mu ----------------- dx*rho*u/mu dt*mu/(dx**2*rho) ----------------- dx*rho*u/mu dt*u/dx ----------------- dt*mu/(dx**2*rho) dt*u/dx ----------------- dx/(dt*u) mu/(dt*rho*u**2) ----------------- mu/(dx*rho*u) dt*u/dx ----------------- dt*rho*u**2/mu dx*rho*u/mu