Table of Contents¶

1 Cholesky Decomposition

1.1 Cholesky decomposition

1.2 Pivoting

1.3 Implementation

1.3.1 Example: positive definite matrix.

1.3.2 Example: positive semi-definite matrix.

1.4 Applications

1.4.1 Multivariate normal density

1.4.2 Linear regression

1.5 Further reading

Cholesky Decomposition¶

A basic tenet in numerical analysis:

The structure should be exploited whenever solving a problem.

Common structures include: symmetry, definiteness, sparsity, Kronecker product, low rank, ...

LU decomposition (Gaussian Elimination) is not used in statistics so often because most of time statisticians deal with positive (semi)definite matrix. (That's why I hate to see solve() in R code.)
Consider solving the normal equation

$$ \mathbf{X}^T \mathbf{X} \beta = \mathbf{X}^T \mathbf{y} $$

for linear regression. The coefficient matrix $\mathbf{X}^T \mathbf{X}$ is symmetric and positive semidefinite. How to exploit this structure?

Cholesky decomposition¶

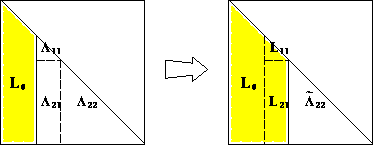
Theorem: Let $\mathbf{A} \in \mathbb{R}^{n \times n}$ be symmetric and positive definite. Then $\mathbf{A} = \mathbf{L} \mathbf{L}^T$, where $\mathbf{L}$ is lower triangular with positive diagonal entries and is unique.

Proof (by induction):
If $n=1$, then $\ell = \sqrt{a}$. For $n>1$, the block equation $$ \begin{eqnarray*} \begin{pmatrix} a_{11} & \mathbf{a}^T \\ \mathbf{a} & \mathbf{A}_{22} \end{pmatrix} = \begin{pmatrix} \ell_{11} & \mathbf{0}_{n-1}^T \\ \mathbf{l} & \mathbf{L}_{22} \end{pmatrix} \begin{pmatrix} \ell_{11} & \mathbf{l}^T \\ \mathbf{0}_{n-1} & \mathbf{L}_{22}^T \end{pmatrix} \end{eqnarray*} $$ has solution $$ \begin{eqnarray*} \ell_{11} &=& \sqrt{a_{11}} \\ \mathbf{l} &=& \ell_{11}^{-1} \mathbf{a} \\ \mathbf{L}_{22} \mathbf{L}_{22}^T &=& \mathbf{A}_{22} - \mathbf{l} \mathbf{l}^T = \mathbf{A}_{22} - a_{11}^{-1} \mathbf{a} \mathbf{a}^T. \end{eqnarray*} $$
Now $a_{11}>0$ (why?), so $\ell_{11}$ and $\mathbf{l}$ are uniquely determined. $\mathbf{A}_{22} - a_{11}^{-1} \mathbf{a} \mathbf{a}^T$ is positive definite because $\mathbf{A}$ is positive definite (why?). By induction hypothesis, $\mathbf{L}_{22}$ exists and is unique.

The constructive proof completely specifies the algorithm:

Computational cost:

$$ \frac{1}{2} [2(n-1)^2 + 2(n-2)^2 + \cdots + 2 \cdot 1^2] \approx \frac{1}{3} n^3 \quad \text{flops} $$

plus $n$ square roots. Half the cost of LU decomposition by utilizing symmetry.

In general Cholesky decomposition is very stable. Failure of the decomposition simply means $\mathbf{A}$ is not positive definite. It is an efficient way to test positive definiteness.

Pivoting¶

When $\mathbf{A}$ does not have full rank, e.g., $\mathbf{X}^T \mathbf{X}$ with a non-full column rank $\mathbf{X}$, we encounter $a_{kk} = 0$ during the procedure.
Symmetric pivoting. At each stage $k$, we permute both row and column such that $\max_{k \le i \le n} a_{ii}$ becomes the pivot. If we encounter $\max_{k \le i \le n} a_{ii} = 0$, then $\mathbf{A}[k:n,k:n] = \mathbf{0}$ (why?) and the algorithm terminates.
With symmetric pivoting:

$$ \mathbf{P} \mathbf{A} \mathbf{P}^T = \mathbf{L} \mathbf{L}^T, $$

where $\mathbf{P}$ is a permutation matrix and $\mathbf{L} \in \mathbb{R}^{n \times r}$, $r = \text{rank}(\mathbf{A})$.

Implementation¶

LAPACK functions: ?potrf (without pivoting), ?pstrf (with pivoting).
Julia functions: cholfact, cholfact!, chol, or call LAPACK wrapper functions potrf! and pstrf!

Example: positive definite matrix.¶

In [1]:

A = [4 12 -16; 12 37 -43; -16 -43 98]

Out[1]:

3×3 Array{Int64,2}:
   4   12  -16
  12   37  -43
 -16  -43   98

In [2]:

# Cholesky without pivoting
Achol = cholfact(A)

Out[2]:

Base.LinAlg.Cholesky{Float64,Array{Float64,2}} with factor:
[2.0 6.0 -8.0; 0.0 1.0 5.0; 0.0 0.0 3.0]

In [3]:

Achol[:L]

Out[3]:

3×3 LowerTriangular{Float64,Array{Float64,2}}:
  2.0   ⋅    ⋅ 
  6.0  1.0   ⋅ 
 -8.0  5.0  3.0

In [4]:

Achol[:U]

Out[4]:

3×3 UpperTriangular{Float64,Array{Float64,2}}:
 2.0  6.0  -8.0
  ⋅   1.0   5.0
  ⋅    ⋅    3.0

In [5]:

b = [1.0; 2.0; 3.0]
A \ b # this does LU; wasteful!; 2/3 n^3 + 2n^2

Out[5]:

3-element Array{Float64,1}:
 28.5833 
 -7.66667
  1.33333

In [6]:

@which A \ b

Out[6]:

\(A::AbstractArray{T,2} where T, B::Union{AbstractArray{T,1}, AbstractArray{T,2}} where T) at linalg/generic.jl:820

In [7]:

Achol \ b # two triangular solves; only 2n^2 flops

Out[7]:

3-element Array{Float64,1}:
 28.5833 
 -7.66667
  1.33333

In [8]:

@which Achol \ b

Out[8]:

\(F::Factorization, B::Union{AbstractArray{T,1}, AbstractArray{T,2}} where T) at linalg/factorization.jl:45

In [9]:

det(A) # this actually does LU; wasteful!

Out[9]:

36.0

In [10]:

@which det(A)

Out[10]:

det{T}(A::AbstractArray{T,2}) at linalg/generic.jl:1222

In [11]:

det(Achol) # cheap

Out[11]:

36.0

In [12]:

@which det(Achol)

Out[12]:

det(C::Base.LinAlg.Cholesky) at linalg/cholesky.jl:495

In [13]:

inv(A) # this does LU!

Out[13]:

3×3 Array{Float64,2}:
  49.3611   -13.5556     2.11111 
 -13.5556     3.77778   -0.555556
   2.11111   -0.555556   0.111111

In [14]:

@which inv(A)

Out[14]:

inv{T}(A::Union{Base.ReshapedArray{T,2,A,MI} where MI<:Tuple{Vararg{Base.MultiplicativeInverses.SignedMultiplicativeInverse{Int64},N} where N} where A<:Union{DenseArray, SubArray{T,N,P,I,true} where I<:Tuple{Union{Base.Slice, UnitRange},Vararg{Any,N} where N} where P where N where T}, DenseArray{T,2}, SubArray{T,2,A,I,L} where L} where I<:Tuple{Vararg{Union{Base.AbstractCartesianIndex, Int64, Range{Int64}},N} where N} where A<:Union{Base.ReshapedArray{T,N,A,MI} where MI<:Tuple{Vararg{Base.MultiplicativeInverses.SignedMultiplicativeInverse{Int64},N} where N} where A<:Union{DenseArray, SubArray{T,N,P,I,true} where I<:Tuple{Union{Base.Slice, UnitRange},Vararg{Any,N} where N} where P where N where T} where N where T, DenseArray}) at linalg/dense.jl:651

In [15]:

inv(Achol)

Out[15]:

3×3 Array{Float64,2}:
  49.3611   -13.5556     2.11111 
 -13.5556     3.77778   -0.555556
   2.11111   -0.555556   0.111111

In [16]:

@which inv(Achol)

Out[16]:

inv(C::Base.LinAlg.Cholesky{#s268,#s267} where #s267<:(Union{Base.ReshapedArray{T,2,A,MI} where MI<:Tuple{Vararg{Base.MultiplicativeInverses.SignedMultiplicativeInverse{Int64},N} where N} where A<:Union{DenseArray, SubArray{T,N,P,I,true} where I<:Tuple{Union{Base.Slice, UnitRange},Vararg{Any,N} where N} where P where N where T}, DenseArray{T,2}, SubArray{T,2,A,I,L} where L} where I<:Tuple{Vararg{Union{Base.AbstractCartesianIndex, Int64, Range{Int64}},N} where N} where A<:Union{Base.ReshapedArray{T,N,A,MI} where MI<:Tuple{Vararg{Base.MultiplicativeInverses.SignedMultiplicativeInverse{Int64},N} where N} where A<:Union{DenseArray, SubArray{T,N,P,I,true} where I<:Tuple{Union{Base.Slice, UnitRange},Vararg{Any,N} where N} where P where N where T} where N where T, DenseArray} where T) where #s268<:Union{Complex{Float32}, Complex{Float64}, Float32, Float64}) at linalg/cholesky.jl:537

Example: positive semi-definite matrix.¶

In [17]:

srand(280) # seed
A = randn(5, 3)
A = A * A'

Out[17]:

5×5 Array{Float64,2}:
  2.06704   -3.10361    2.41766    -0.717719   0.845433 
 -3.10361    9.76269   -7.31094     2.14335    0.283818 
  2.41766   -7.31094    6.0473     -0.931321  -0.0610487
 -0.717719   2.14335   -0.931321    1.28376    0.115462 
  0.845433   0.283818  -0.0610487   0.115462   0.827396

In [18]:

Achol = cholfact(A)

Base.LinAlg.PosDefException(5)

Stacktrace:
 [1] _chol!(::Array{Float64,2}, ::Type{UpperTriangular}) at ./linalg/cholesky.jl:55
 [2] cholfact!(::Hermitian{Float64,Array{Float64,2}}, ::Type{Val{false}}) at ./linalg/cholesky.jl:211
 [3] cholfact(::Array{Float64,2}, ::Symbol) at ./linalg/cholesky.jl:350
 [4] cholfact(::Array{Float64,2}) at ./linalg/cholesky.jl:349

In [19]:

Achol = cholfact(A, :L, Val{true}) # 3rd argument request partial pivoting

Out[19]:

Base.LinAlg.CholeskyPivoted{Float64,Array{Float64,2}}([3.12453 -3.10361 … -0.717719 0.845433; -0.993306 1.03941 … 2.14335 0.283818; … ; -2.33985 0.0899256 … 5.96046e-8 0.115462; 0.0908354 0.900181 … -1.19908e-8 0.0], 'L', [2, 1, 4, 3, 5], 4, 0.0, 1)

In [20]:

rank(Achol) # determine rank from Cholesky factor

Out[20]:

In [21]:

rank(A) # determine rank from SVD, which is more numerically stable

Out[21]:

In [22]:

Achol[:L]

Out[22]:

5×5 LowerTriangular{Float64,Array{Float64,2}}:
  3.12453      ⋅          ⋅           ⋅           ⋅ 
 -0.993306    1.03941     ⋅           ⋅           ⋅ 
  0.685974   -0.0349591  0.901097     ⋅           ⋅ 
 -2.33985     0.0899256  0.751198    5.96046e-8   ⋅ 
  0.0908354   0.900181   0.0939082  -1.19908e-8  0.0

In [23]:

Achol[:U]

Out[23]:

5×5 UpperTriangular{Float64,Array{Float64,2}}:
 3.12453  -0.993306   0.685974   -2.33985      0.0908354 
  ⋅        1.03941   -0.0349591   0.0899256    0.900181  
  ⋅         ⋅         0.901097    0.751198     0.0939082 
  ⋅         ⋅          ⋅          5.96046e-8  -1.19908e-8
  ⋅         ⋅          ⋅           ⋅           0.0

In [24]:

Achol[:p]

Out[24]:

5-element Array{Int64,1}:
 2
 1
 4
 3
 5

In [25]:

# P A P' = L U
vecnorm(Achol[:P] * A * Achol[:P]' - Achol[:L] * Achol[:U])

Out[25]:

1.7763568394002505e-15

Applications¶

No inversion mentality: Whenever we see matrix inverse, we should think in terms of solving linear equations. If the matrix is positive (semi)definite, use Cholesky decomposition, which is twice cheaper than LU decomposition.

Multivariate normal density¶

Multivariate normal density $\text{MVN}(\mu, \Sigma)$, where $\Sigma$ is p.d., is

$$ - \frac{n}{2} \log (2\pi) - \frac{1}{2} \log \det \Sigma - \frac{1}{2} (\mathbf{y} - \mu)^T \Sigma^{-1} (\mathbf{y} - \mu). $$

Method 1: (a) compute explicit inverse $\Sigma^{-1}$ ($2n^3$ flops), (b) compute quadratic form ($2n^2 + 2n$ flops), (c) compute determinant ($2n^3/3$ flops).
Method 2: (a) Cholesky decomposition $\Sigma = \mathbf{L} \mathbf{L}^T$ ($n^3/3$ flops), (b) Solve $\mathbf{L} \mathbf{x} = \mathbf{y} - \mu$ by forward substitutions ($n^2$ flops), (c) compute quadratic form $\mathbf{x}^T \mathbf{x}$ ($2n$ flops), and (d) compute determinant from Cholesky factor ($n$ flops).

Which method is better?

In [26]:

# this is a person w/o any numerical analsyis training
function logpdf_mvn_1(y::Vector, Σ::Matrix)
    n = length(y)
    - (n//2) * log(2π) - (1//2) * logdet(Σ) - (1//2) * y' * inv(Σ) * y
end

# this is an efficiency-savvy person 
function logpdf_mvn_2(y::Vector, Σ::Matrix)
    n = length(y)
    Σchol = cholfact(Symmetric(Σ))
    - (n//2) * log(2π) - (1//2) * logdet(Σchol) - (1//2) * sum(abs2, Σchol[:L] \ y)
end

# better memory efficiency
function logpdf_mvn_3(y::Vector, Σ::Matrix)
    n = length(y)
    Σchol = cholfact(Symmetric(Σ))
    - (n//2) * log(2π) - (1//2) * logdet(Σchol) - (1//2) * dot(y, Σchol \ y)
end

Out[26]:

logpdf_mvn_3 (generic function with 1 method)

In [27]:

using BenchmarkTools, Distributions

srand(280) # seed

n = 1000
Σ = randn(n, n); Σ = Σ' * Σ + I # covariance matrix
y = rand(MvNormal(Σ)) # one randdom sample from N(0, Σ)

# at least they give same answer
@show logpdf_mvn_1(y, Σ)
@show logpdf_mvn_2(y, Σ)
@show logpdf_mvn_3(y, Σ);

logpdf_mvn_1(y, Σ) = -4396.173284372774
logpdf_mvn_2(y, Σ) = -4396.173284372773
logpdf_mvn_3(y, Σ) = -4396.173284372773

In [28]:

@benchmark logpdf_mvn_1(y, Σ)

Out[28]:

BenchmarkTools.Trial: 
  memory estimate:  23.42 MiB
  allocs estimate:  26
  --------------
  minimum time:     68.818 ms (2.48% GC)
  median time:      77.068 ms (2.30% GC)
  mean time:        81.321 ms (2.25% GC)
  maximum time:     131.659 ms (2.40% GC)
  --------------
  samples:          62
  evals/sample:     1

In [29]:

@benchmark logpdf_mvn_2(y, Σ)

Out[29]:

BenchmarkTools.Trial: 
  memory estimate:  15.27 MiB
  allocs estimate:  14
  --------------
  minimum time:     10.761 ms (0.00% GC)
  median time:      12.785 ms (13.40% GC)
  mean time:        12.987 ms (10.33% GC)
  maximum time:     19.108 ms (10.46% GC)
  --------------
  samples:          385
  evals/sample:     1

In [30]:

@benchmark logpdf_mvn_3(y, Σ)

Out[30]:

BenchmarkTools.Trial: 
  memory estimate:  7.64 MiB
  allocs estimate:  10
  --------------
  minimum time:     8.802 ms (0.00% GC)
  median time:      9.325 ms (0.00% GC)
  mean time:        10.130 ms (7.36% GC)
  maximum time:     14.764 ms (15.79% GC)
  --------------
  samples:          493
  evals/sample:     1

To evaluate same multivariate normal density at many observations $y_1, y_2, \ldots$, we pre-compute the Cholesky decomposition ($n^3/3$ flops), then each evaluation costs $n^2$ flops.

Linear regression¶

Cholesky decomposition is one approach to solve linear regression.
- Compute $\mathbf{X}^T \mathbf{X}$: $np^2$ flops
- Compute $\mathbf{X}^T \mathbf{y}$: $2np$ flops
- Cholesky decomposition of $\mathbf{X}^T \mathbf{X}$: $\frac{1}{3} p^3$ flops
- Solve normal equation $\mathbf{X}^T \mathbf{X} \beta = \mathbf{X}^T \mathbf{y}$: $2p^2$ flops
- If need standard errors, another $(4/3)p^3$ flops

Total computational cost is $np^2 + (1/3) p^3$ (without s.e.) or $np^2 + (5/3) p^3$ (with s.e.) flops.