versioninfo()
Julia Version 1.1.0 Commit 80516ca202 (2019-01-21 21:24 UTC) Platform Info: OS: macOS (x86_64-apple-darwin14.5.0) CPU: Intel(R) Core(TM) i7-6920HQ CPU @ 2.90GHz WORD_SIZE: 64 LIBM: libopenlibm LLVM: libLLVM-6.0.1 (ORCJIT, skylake) Environment: JULIA_EDITOR = code
QR Decomposition¶
We learnt Cholesky decomposition as one approach for solving linear regression.
A second approach for linear regression uses QR decomposition.
This is how thelm()function in R does linear regression.
using Random
Random.seed!(280) # seed
n, p = 5, 3
X = randn(n, p) # predictor matrix
y = randn(n) # response vector
# finds the least squares solution
X \ y
3-element Array{Float64,1}:
0.3795466676698624
0.6508866456093488
0.392250419565355
We want to understand what is QR and how it is used for solving least squares problem.
Definition¶
Assume $\mathbf{X} \in \mathbb{R}^{n \times p}$ has full column rank.
Full QR decomposition:
where
- $\mathbf{Q} \in \mathbb{R}^{n \times n}$, $\mathbf{Q}^T \mathbf{Q} = \mathbf{I}_n$. In other words, $\mathbf{Q}$ is an orthogonal matrix.
- First $p$ columns of $\mathbf{Q}$ form an orthonormal basis of ${\cal C}(\mathbf{X})$ (column space of $\mathbf{X}$)
- Last $n-p$ columns of $\mathbf{Q}$ form an orthonormal basis of ${\cal N}(\mathbf{X}^T)$ (null space of $\mathbf{X}^T$)
- $\mathbf{R} \in \mathbb{R}^{n \times p}$ is upper triangular with positive diagonal entries.
- Skinny (or thin) QR decomposition:
where
- $\mathbf{Q}_1 \in \mathbb{R}^{n \times p}$, $\mathbf{Q}_1^T \mathbf{Q}_1 = \mathbf{I}_p$. In other words, $\mathbf{Q}_1$ has orthonormal columns.
- $\mathbf{R}_1 \in \mathbb{R}^{p \times p}$ is an upper triangular matrix with positive diagonal entries.
- Given QR decompositin $\mathbf{X} = \mathbf{Q} \mathbf{R}$,
Therefore $\mathbf{R}$ is the same as the upper triangular Choleksy factor of the Gram matrix $\mathbf{X}^T \mathbf{X}$.
There are 3 algorithms to compute QR: (modified) Gram-Schmidt, Householder transform, (fast) Givens transform.
In particular, the Householder transform for QR is implemented in LAPACK and thus used in R and Julia.
Algorithms¶
QR by Gram-Schmidt¶


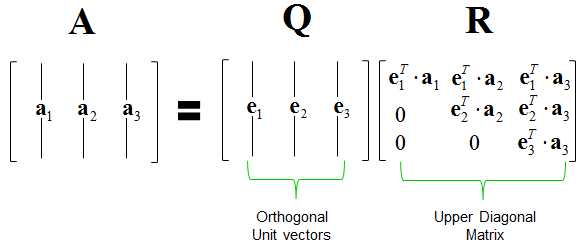
Assume $\mathbf{X} = (\mathbf{x}_1, \ldots, \mathbf{x}_p) \in \mathbb{R}^{n \times p}$ has full column rank.
Gram-Schmidt (GS) algorithm produces the skinny QR:
where $\mathbf{Q} \in \mathbb{R}^{n \times p}$ has orthonormal columns and $\mathbf{R} \in \mathbb{R}^{p \times p}$ is an upper triangular matrix.
Gram-Schmidt algorithm orthonormalizes a set of non-zero, linearly independent vectors $\mathbf{x}_1,\ldots,\mathbf{x}_p$.
- Initialize $\mathbf{q}_1 = \mathbf{x}_1 / \|\mathbf{x}_1\|_2$
- For $k=2, \ldots, p$,
Collectively we have $\mathbf{X} = \mathbf{Q} \mathbf{R}$.
- $\mathbf{Q} \in \mathbb{R}^{n \times p}$ has orthonormal columns $\mathbf{q}_k$ thus $\mathbf{Q}^T \mathbf{Q} = \mathbf{I}_p$
- Where is $\mathbf{R}$? $\mathbf{R} = \mathbf{Q}^T \mathbf{X}$ has entries $r_{jk} = \langle \mathbf{q}_j, \mathbf{x}_k \rangle$, which are computed during the Gram-Schmidt process. Note $r_{jk} = 0$ for $j > k$, so $\mathbf{R}$ is upper triangular.
In GS algorithm, $\mathbf{X}$ is over-written by $\mathbf{Q}$ and $\mathbf{R}$ is stored in a separate array.
The regular Gram-Schmidt is unstable (we loose orthogonality due to roundoff errors) when columns of $\mathbf{X}$ are collinear.
Modified Gram-Schmidt (MGS): after each normalization step of $\mathbf{v}_k$, we replace columns $\mathbf{x}_j$, $j>k$, by its residual.
Why MGS is better than GS? Read http://cavern.uark.edu/~arnold/4353/CGSMGS.pdf
Computational cost of GS and MGS is $\sum_{k=1}^p 4n(k-1) \approx 2np^2$.
QR by Householder transform¶

This is the algorithm implemented in LAPACK. In other words, this is the algorithm for solving linear regression in R.
Assume $\mathbf{X} = (\mathbf{x}_1, \ldots, \mathbf{x}_p) \in \mathbb{R}^{n \times p}$ has full column rank.
Idea:
where $\mathbf{H}_j \in \mathbf{R}^{n \times n}$ are a sequence of Householder transformation matrices.
It yields the **full QR** where $\mathbf{Q} = \mathbf{H}_1 \cdots \mathbf{H}_p \in \mathbb{R}^{n \times n}$. Recall that GS/MGS only produces the **thin QR** decomposition.
- For arbitrary $\mathbf{v}, \mathbf{w} \in \mathbb{R}^{n}$ with $\|\mathbf{v}\|_2 = \|\mathbf{w}\|_2$, we can construct a Householder matrix (or Householder reflector)
that transforms $\mathbf{v}$ to $\mathbf{w}$: $$ \mathbf{H} \mathbf{v} = \mathbf{w}. $$ $\mathbf{H}$ is symmetric and orthogonal. Calculation of Householder vector $\mathbf{u}$ costs $4n$ flops for general $\mathbf{u}$ and $\mathbf{w}$.

- Now choose $\mathbf{H}_1$ to zero the first column of $\mathbf{X}$ below diagonal
Take $\mathbf{H}_2$ to zero the second column below diagonal; ...
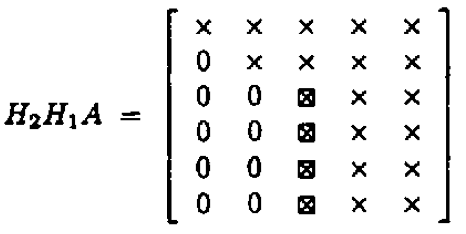
In general, choose the $j$-th Householder transform $\mathbf{H}_j = \mathbf{I}_n - 2 \mathbf{u}_j \mathbf{u}_j^T$, where $$ \mathbf{u}_j = \begin{pmatrix} \mathbf{0}_{j-1} \\ {\tilde u}_j \end{pmatrix}, \quad {\tilde u}_j \in \mathbb{R}^{n-j+1}, $$ to zero the $j$-th column below diagonal. $\mathbf{H}_j$ takes the form $$ \mathbf{H}_j = \begin{pmatrix} \mathbf{I}_{j-1} & \\ & \mathbf{I}_{n-j+1} - 2 {\tilde u}_j {\tilde u}_j^T \end{pmatrix} = \begin{pmatrix} \mathbf{I}_{j-1} & \\ & {\tilde H}_{j} \end{pmatrix}. $$
- Applying a Householder transform $\mathbf{H} = \mathbf{I} - 2 \mathbf{u} \mathbf{u}^T$ to a matrix $\mathbf{X} \in \mathbb{R}^{n \times p}$
costs $4np$ flops. Householder updates never entails explicit formation of the Householder matrices.
Note applying ${\tilde H}_j$ to $\mathbf{X}$ only needs $4(n-j+1)(p-j+1)$ flops.
QR by Householder: $\mathbf{H}_{p} \cdots \mathbf{H}_1 \mathbf{X} = \begin{pmatrix} \mathbf{R}_1 \\ \mathbf{0} \end{pmatrix}$.
The process is done in place. Upper triangular part of $\mathbf{X}$ is overwritten by $\mathbf{R}_1$ and the essential Householder vectors ($\tilde u_{j1}$ is normalized to 1) are stored in $\mathbf{X}[j:n,j]$.
At $j$-th stage 0. computing the Householder vector ${\tilde u}_j$ costs $3(n-j+1)$ flops 0. applying the Householder transform ${\tilde H}_j$ to the $\mathbf{X}[j:n, j:p]$ block costs $4(n-j+1)(p-j+1)$ flops
In total we need $\sum_{j=1}^p [3(n-j+1) + 4(n-j+1)(p-j+1)] \approx 2np^2 - \frac 23 p^3$ flops.
Where is $\mathbf{Q}$? $\mathbf{Q} = \mathbf{H}_1 \cdots \mathbf{H}_p$. In some applications, it's necessary to form the orthogonal matrix $\mathbf{Q}$.
Accumulating $\mathbf{Q}$ costs another $2np^2 - \frac 23 p^3$ flops.
When computing $\mathbf{Q}^T \mathbf{v}$ or $\mathbf{Q} \mathbf{v}$ as in some applications (e.g., solve linear equation using QR), no need to form $\mathbf{Q}$. Simply apply Householder transforms successively to the vector $\mathbf{v}$.
Computational cost of Householder QR for linear regression: $2n p^2 - \frac 23 p^3$ (regression coefficients and $\hat \sigma^2$) or more (fitted values, s.e., ...).
Householder QR with column pivoting¶
Consider rank deficient $\mathbf{X}$.
- At the $j$-th stage, swap the column in $\mathbf{X}[j:n,j:p]$ with maximum $\ell_2$ norm to be the pivot column. If the maximum $\ell_2$ norm is 0, it stops, ending with
where $\mathbf{P} \in \mathbb{R}^{p \times p}$ is a permutation matrix and $r$ is the rank of $\mathbf{X}$. QR with column pivoting is rank revealing.
- The overhead of re-computing the column norms can be reduced by the property
for any orthogonal matrix $\mathbf{Q}$.
using Random, LinearAlgebra
Random.seed!(280) # seed
y = randn(5) # response vector
X = randn(5, 3) # predictor matrix
5×3 Array{Float64,2}:
-1.12783 -0.88267 -1.79426
1.14786 1.71384 1.09138
-1.35471 -0.733952 0.426628
-0.237065 1.08182 -0.624434
-0.680994 -0.170406 0.0320486
X \ y # least squares solution by QR
3-element Array{Float64,1}:
-0.6130947263291079
-0.7800615507222621
0.3634934302764104
# same as
qr(X) \ y
3-element Array{Float64,1}:
-0.6130947263291078
-0.7800615507222622
0.3634934302764104
cholesky(X'X) \ (X'y) # least squares solution by Cholesky
3-element Array{Float64,1}:
-0.6130947263291076
-0.7800615507222624
0.3634934302764099
# QR factorization with column pivoting
xqr = qr(X, Val(true))
QRPivoted{Float64,Array{Float64,2}}
Q factor:
5×5 LinearAlgebra.QRPackedQ{Float64,Array{Float64,2}}:
-0.377941 -0.70935 -0.0804225 -0.586254 -0.0618207
0.733832 0.161768 -0.101458 -0.650763 -0.039191
-0.314263 0.384947 -0.75494 -0.116185 -0.411851
0.463213 -0.565162 -0.483764 0.464867 -0.12608
-0.0729644 0.0553323 -0.423411 -0.0566828 0.899514
R factor:
3×3 Array{Float64,2}:
2.33547 1.05335 1.6342
0.0 1.96822 0.560522
0.0 0.0 1.39999
permutation:
3-element Array{Int64,1}:
2
3
1
xqr \ y # least squares solution
3-element Array{Float64,1}:
-0.6130947263291079
-0.7800615507222621
0.3634934302764104
# thin Q matrix multiplication (a sequence of Householder transforms)
norm(xqr.Q * xqr.R - X[:, xqr.p]) # recovers X (with columns permuted)
9.924559042135032e-16
QR by Givens rotation¶
Householder transform $\mathbf{H}_j$ introduces batch of zeros into a vector.
Givens transform (aka Givens rotation, Jacobi rotation, plane rotation) selectively zeros one element of a vector.
Overall QR by Givens rotation is less efficient than the Householder method, but is better suited for matrices with structured patterns of nonzero elements.
Givens/Jacobi rotations:
where $c = \cos(\theta)$ and $s = \sin(\theta)$. $\mathbf{G}(i,k,\theta)$ is orthogonal.
- Pre-multiplication by $\mathbf{G}(i,k,\theta)^T$ rotates counterclockwise $\theta$ radians in the $(i,k)$ coordinate plane. If $\mathbf{x} \in \mathbb{R}^n$ and $\mathbf{y} = \mathbf{G}(i,k,\theta)^T \mathbf{x}$, then
Apparently if we choose $\tan(\theta) = -x_k / x_i$, or equivalently, $$ \begin{eqnarray*} c = \frac{x_i}{\sqrt{x_i^2 + x_k^2}}, \quad s = \frac{-x_k}{\sqrt{x_i^2 + x_k^2}}, \end{eqnarray*} $$ then $y_k=0$.
- Pre-applying Givens transform $\mathbf{G}(i,k,\theta)^T \in \mathbb{R}^{n \times n}$ to a matrix $\mathbf{A} \in \mathbb{R}^{n \times m}$ only effects two rows of $\mathbf{
A}$: $$ \mathbf{A}([i, k], :) \gets \begin{pmatrix} c & s \\ -s & c \end{pmatrix}^T \mathbf{A}([i, k], :), $$ costing $6m$ flops.
- Post-applying Givens transform $\mathbf{G}(i,k,\theta) \in \mathbb{R}^{m \times m}$ to a matrix $\mathbf{A} \in \mathbb{R}^{n \times m}$ only effects two columns of $\mathbf{A}$:
costing $6n$ flops.
- QR by Givens: $\mathbf{G}_t^T \cdots \mathbf{G}_1^T \mathbf{X} = \begin{pmatrix} \mathbf{R}_1 \\ \mathbf{0} \end{pmatrix}$.
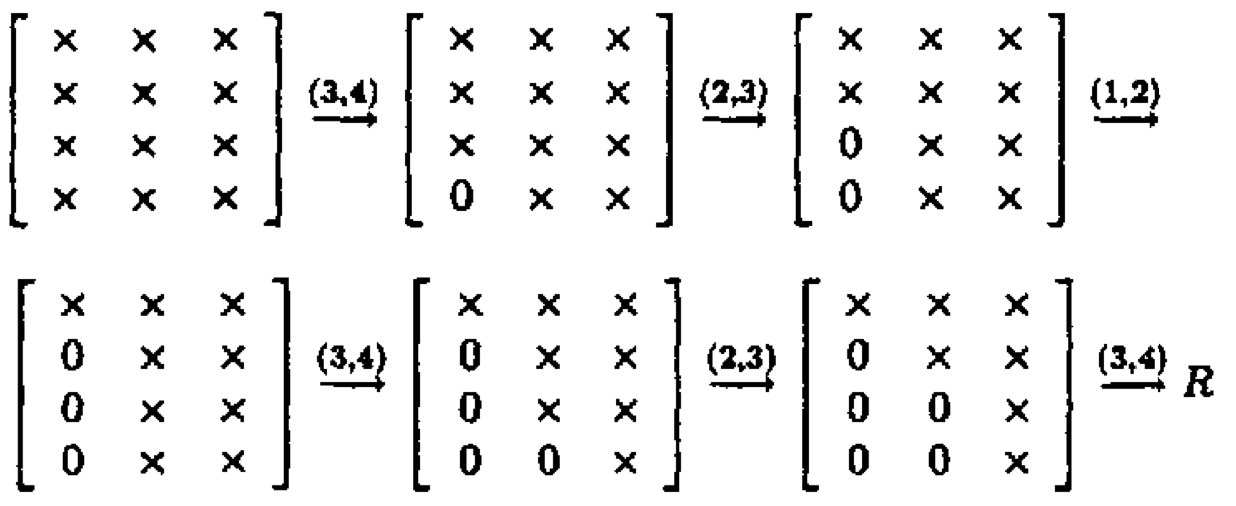
Zeros in $\mathbf{X}$ can also be introduced row-by-row.
If $\mathbf{X} \in \mathbb{R}^{n \times p}$, the total cost is $3np^2 - p^3$ flops and $O(np)$ square roots.
Note each Givens transform can be summarized by a single number, which is stored in the zeroed entry of $\mathbf{X}$.
Fast Givens transform avoids taking square roots.
Further reading¶
Section 7.8 of Numerical Analysis for Statisticians of Kenneth Lange (2010).
Section II.5.3 of Computational Statistics by James Gentle (2010).
Chapter 5 of Matrix Computation by Gene Golub and Charles Van Loan (2013).