Table of Contents¶

Convexity, Duality, and Optimality Conditions (KL Chapter 11, BV Chapter 5)¶

Convexity¶

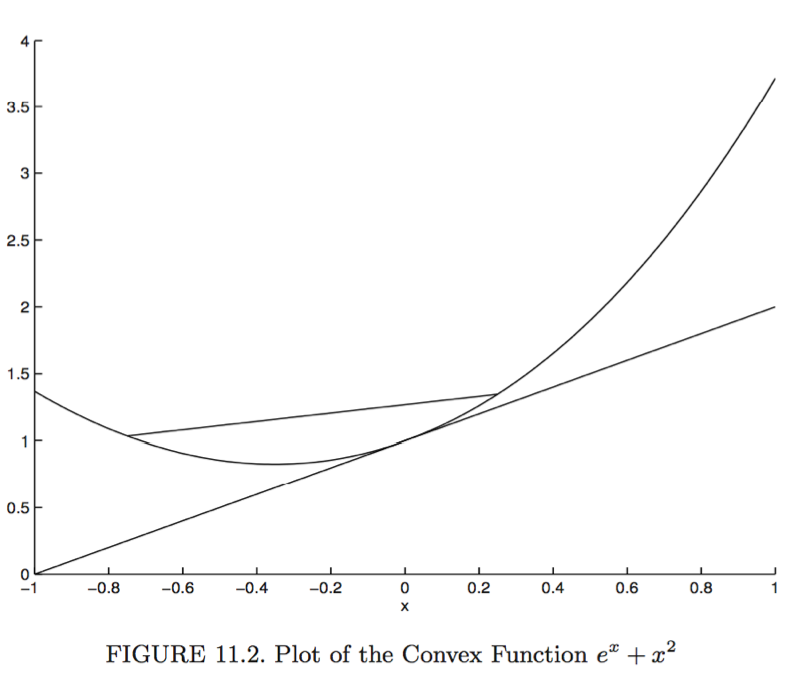
• A function $f: \mathbb{R}^n \mapsto \mathbb{R}$ is convex if

  1. $\text{dom} f$ is a convex set: $\lambda \mathbf{x} + (1-\lambda) \mathbf{y} \in \text{dom} f$ for all $\mathbf{x},\mathbf{y} \in \text{dom} f$ and any $\lambda \in (0, 1)$, and
  2. $f(\lambda \mathbf{x} + (1-\lambda) \mathbf{y}) \le \lambda f(\mathbf{x}) + (1-\lambda) f(\mathbf{y})$, for all $\mathbf{x},\mathbf{y} \in \text{dom} f$ and $\lambda \in (0,1)$.

• $f$ is strictly convex if the inequality is strict for all $\mathbf{x} \ne \mathbf{y} \in \text{dom} f$ and $\lambda$.

• Supporting hyperplane inequality. A differentiable function $f$ is convex if and only if

$$ f(\mathbf{x}) \ge f(\mathbf{y}) + \nabla f(\mathbf{y})^T (\mathbf{x}-\mathbf{y}) $$

for all $\mathbf{x}, \mathbf{y} \in \text{dom} f$.

• Second-order condition for convexity. A twice differentiable function $f$ is convex if and only if $\nabla^2f(\mathbf{x})$ is psd for all $\mathbf{x} \in \text{dom} f$. It is strictly convex if and only if $\nabla^2f(\mathbf{x})$ is pd for all $\mathbf{x} \in \text{dom} f$.

• Convexity and global optima. Suppose $f$ is a convex function.

  1. Any stationary point $\mathbf{y}$, i.e., $\nabla f(\mathbf{y})=\mathbf{0}$, is a global minimum. (Proof: By supporting hyperplane inequality, $f(\mathbf{x}) \ge f(\mathbf{y}) + \nabla f(\mathbf{y})^T (\mathbf{x} - \mathbf{y}) = f(\mathbf{y})$ for all $\mathbf{x} \in \text{dom} f$.)
  2. Any local minimum is a global minimum.
  3. The set of (global) minima is convex.
  4. If $f$ is strictly convex, then the global minimum, if exists, is unique.

• Example: Least squares estimate. $f(\beta) = \frac 12 \| \mathbf{y} - \mathbf{X} \beta \|_2^2$ has Hessian $\nabla^2f = \mathbf{X}^T \mathbf{X}$ which is psd. So $f$ is convex and any stationary point (solution to the normal equation) is a global minimum. When $\mathbf{X}$ is rank deficient, the set of solutions is convex.

• Jensen's inequality. If $h$ is convex and $\mathbf{W}$ a random vector taking values in $\text{dom} f$, then

$$ \mathbf{E}[h(\mathbf{W})] \ge h [\mathbf{E}(\mathbf{W})], $$

provided both expectations exist. For a strictly convex $h$, equality holds if and only if $W = \mathbf{E}(W)$ almost surely.

Proof: Take $\mathbf{x} = \mathbf{W}$ and $\mathbf{y} = \mathbf{E} (\mathbf{W})$ in the supporting hyperplane inequality.

• Information inequality. Let $f$ and $g$ be two densities with respect to a common measure $\mu$ and $f, g>0$ almost everywhere relative to $\mu$. Then

$$ \mathbf{E}_f (\log f) \ge \mathbf{E}_f (\log g), $$

with equality if and only if $f = g$ almost everywhere on $\mu$.

Proof: Apply Jensen's inequality to the convex function $- \ln(t)$ and random variable $W=g(X)/f(X)$ where $X \sim f$.

Important applications of information inequality: M-estimation, EM algorithm.

Duality¶

• Consider optimization problem

\begin{eqnarray*} &\text{minimize}& f_0(\mathbf{x}) \\ &\text{subject to}& f_i(\mathbf{x}) \le 0, \quad i = 1,\ldots,m \\ & & h_i(\mathbf{x}) = 0, \quad i = 1,\ldots,p. \end{eqnarray*}

• The Lagrangian is

\begin{eqnarray*} L(\mathbf{x}, \lambda, \nu) = f_0(\mathbf{x}) + \sum_{i=1}^m \lambda_i f_i(\mathbf{x}) + \sum_{i=1}^p \nu_i h_i(\mathbf{x}). \end{eqnarray*}

The vectors $\lambda = (\lambda_1,\ldots, \lambda_m)^T$ and $\nu = (\nu_1,\ldots,\nu_p)^T$ are called the Lagrange multiplier vectors or dual variables.

• The Lagrange dual function is the minimum value of the Langrangian over $\mathbf{x}$

\begin{eqnarray*} g(\lambda, \mu) = \inf_{\mathbf{x}} L(\mathbf{x}, \lambda, \nu) = \inf_{\mathbf{x}} \left( f_0(\mathbf{x}) + \sum_{i=1}^m \lambda_i f_i(\mathbf{x}) + \sum_{i=1}^p \nu_i h_i(\mathbf{x}) \right). \end{eqnarray*}

• Denote the optimal value of original problem by $p^\star$. For any $\lambda \succeq \mathbf{0}$ and any $\nu$, we have

\begin{eqnarray*} g(\lambda, \nu) \le p^\star. \end{eqnarray*}

Proof: For any feasible point $\tilde{\mathbf{x}}$, \begin{eqnarray*} L(\tilde{\mathbf{x}}, \lambda, \nu) = f_0(\tilde{\mathbf{x}}) + \sum_{i=1}^m \lambda_i f_i(\tilde{\mathbf{x}}) + \sum_{i=1}^p \nu_i h_i(\tilde{\mathbf{x}}) \le f_0(\tilde{\mathbf{x}}) \end{eqnarray*} because the second term is non-positive and the third term is zero. Then \begin{eqnarray*} g(\lambda, \mu) = \inf_{\mathbf{x}} L(\mathbf{x}, \lambda, \mu) \le L(\tilde{\mathbf{x}}, \lambda, \nu) \le f_0(\tilde{\mathbf{x}}). \end{eqnarray*}

• Since each pair $(\lambda, \nu)$ with $\lambda \succeq \mathbf{0}$ gives a lower bound to the optimal value $p^\star$. It is natural to ask for the best possible lower bound the Lagrange dual function can provide. This leads to the Lagrange dual problem

\begin{eqnarray*} &\text{maximize}& g(\lambda, \nu) \\ &\text{subject to}& \lambda \succeq \mathbf{0}, \end{eqnarray*}

which is a convex problem regardless the primal problem is convex or not.

• We denote the optimal value of the Lagrange dual problem by $d^\star$, which satifies the week duality

\begin{eqnarray*} d^\star \le p^\star. \end{eqnarray*}

The difference $p^\star - d^\star$ is called the optimal duality gap.

• If the primal problem is convex, that is

\begin{eqnarray*} &\text{minimize}& f_0(\mathbf{x}) \\ &\text{subject to}& f_i(\mathbf{x}) \le 0, \quad i = 1,\ldots,m \\ & & \mathbf{A} \mathbf{x} = \mathbf{b}, \end{eqnarray*}

with $f_0,\ldots,f_m$ convex, we usually (but not always) have the strong duality, i.e., $d^\star = p^\star$.

• The conditions under which strong duality holds are called constraint qualifications. A commonly used one is Slater's condition: There exists a point in the relative interior of the domain such that

\begin{eqnarray*} f_i(\mathbf{x}) < 0, \quad i = 1,\ldots,m, \quad \mathbf{A} \mathbf{x} = \mathbf{b}. \end{eqnarray*}

Such a point is also called strictly feasible.

KKT optimality conditions¶

KKT is "one of the great triumphs of 20th century applied mathematics" (KL Chapter 11).

Nonconvex problems¶

• Assume $f_0,\ldots,f_m,h_1,\ldots,h_p$ are differentiable. Let $\mathbf{x}^\star$ and $(\lambda^\star, \nu^\star)$ be any primal and dual optimal points with zero duality gap, i.e., strong duality holds.

• Since $\mathbf{x}^\star$ minimizes $L(\mathbf{x}, \lambda^\star, \nu^\star)$ over $\mathbf{x}$, its gradient vanishes at $\mathbf{x}^\star$, we have the Karush-Kuhn-Tucker (KKT) conditions

\begin{eqnarray*} f_i(\mathbf{x}^\star) &\le& 0, \quad i = 1,\ldots,m \\ h_i(\mathbf{x}^\star) &=& 0, \quad i = 1,\ldots,p \\ \lambda_i^\star &\ge& 0, \quad i = 1,\ldots,m \\ \lambda_i^\star f_i(\mathbf{x}^\star) &=& 0, \quad i=1,\ldots,m \\ \nabla f_0(\mathbf{x}^\star) + \sum_{i=1}^m \lambda_i^\star \nabla f_i(\mathbf{x}^\star) + \sum_{i=1}^p \nu_i^\star \nabla h_i(\mathbf{x}^\star) &=& \mathbf{0}. \end{eqnarray*}

• The fourth condition (complementary slackness) follows from

\begin{eqnarray*} f_0(\mathbf{x}^\star) &=& g(\lambda^\star, \nu^\star) \\ &=& \inf_{\mathbf{x}} \left( f_0(\mathbf{x}) + \sum_{i=1}^m \lambda_i^\star f_i(\mathbf{x}) + \sum_{i=1}^p \nu_i^\star h_i(\mathbf{x}) \right) \\ &\le& f_0(\mathbf{x}^\star) + \sum_{i=1}^m \lambda_i^\star f_i(\mathbf{x}^\star) + \sum_{i=1}^p \nu_i^\star h_i(\mathbf{x}^\star) \\ &\le& f_0(\mathbf{x}^\star). \end{eqnarray*}

Since $\sum_{i=1}^m \lambda_i^\star f_i(\mathbf{x}^\star)=0$ and each term is non-positive, we have $\lambda_i^\star f_i(\mathbf{x}^\star)=0$, $i=1,\ldots,m$.

• To summarize, for any optimization problem with differentiable objective and constraint functions for which strong duality obtains, any pair of primal and dual optimal points must satisfy the KKT conditions.

Convex problems¶

• When the primal problem is convex, the KKT conditions are also sufficient for the points to be primal and dual optimal.

• If $f_i$ are convex and $h_i$ are affine, and $(\tilde{\mathbf{x}}, \tilde \lambda, \tilde \nu)$ satisfy the KKT conditions, then $\tilde{\mathbf{x}}$ and $(\tilde \lambda, \tilde \nu)$ are primal and dual optimal, with zero duality gap.

• The KKT conditions play an important role in optimization. Many algorithms for convex optimization are conceived as, or can be interpreted as, methods for solving the KKT conditions.