Required R packages¶

Iterative Methods for Solving Linear Equations¶

Introduction¶

So far we have considered direct methods for solving linear equations.

• Direct methods (flops fixed a priori) vs iterative methods:
  • Direct method (GE/LU, Cholesky, QR, SVD): accurate. good for dense, small to moderate sized $\mathbf{A}$
  • Iterative methods (Jacobi, Gauss-Seidal, SOR, conjugate-gradient, GMRES): accuracy depends on number of iterations. good for large, sparse, structured linear system, parallel computing, warm start (reasonable accuracy after, say, 100 iterations)

Motivation: PageRank¶

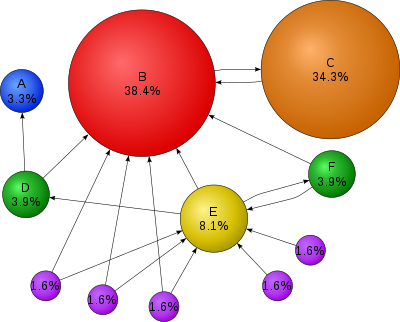
Source: Wikepedia

• $\mathbf{A} \in \{0,1\}^{n \times n}$ the connectivity matrix of webpages with entries

$$ \begin{eqnarray*} a_{ij} = \begin{cases} 1 & \text{if page $i$ links to page $j$} \\ 0 & \text{otherwise} \end{cases}. \end{eqnarray*} $$

$n \approx 10^9$ in May 2017.

• $r_i = \sum_j a_{ij}$ is the out-degree of page $i$.

• Larry Page imagined a random surfer wandering on internet according to following rules:

  • From a page $i$ with $r_i>0$
    • with probability $p$, (s)he randomly chooses a link $j$ from page $i$ (uniformly) and follows that link to the next page
    • with probability $1-p$, (s)he randomly chooses one page from the set of all $n$ pages (uniformly) and proceeds to that page
  • From a page $i$ with $r_i=0$ (a dangling page), (s)he randomly chooses one page from the set of all $n$ pages (uniformly) and proceeds to that page

• The process defines an $n$-state Markov chain, where each state corresponds to each page.

$$ p_{ij} = (1-p)\frac{1}{n} + p\frac{a_{ij}}{r_i} $$

with interpretation $a_{ij}/r_i = 1/n$ if $r_i = 0$.

• Stationary distribution of this Markov chain gives the score (long term probability of visit) of each page.

• Stationary distribution can be obtained as the top left eigenvector of the transition matrix $\mathbf{P}=(p_{ij})$ corresponding to eigenvalue 1.

$$ \mathbf{x}^T\mathbf{P} = \mathbf{x}^T. $$

Equivalently it can be cast as a linear equation. $$ (\mathbf{I} - \mathbf{P}^T) \mathbf{x} = \mathbf{0}. $$

• You've got to solve a linear equation with $10^9$ variables!

• GE/LU will take $2 \times (10^9)^3/3/10^{12} \approx 6.66 \times 10^{14}$ seconds $\approx 20$ million years on a tera-flop supercomputer!

• Iterative methods come to the rescue.

Splitting and fixed point iteration¶

• The key idea of iterative method for solving $\mathbf{A}\mathbf{x}=\mathbf{b}$ is to split the matrix $\mathbf{A}$ so that

$$ \mathbf{A} = \mathbf{M} - \mathbf{K} $$

where $\mathbf{M}$ is invertible and easy to invert.

• Then $\mathbf{A}\mathbf{x} = \mathbf{M}\mathbf{x} - \mathbf{K}\mathbf{x} = \mathbf{b}$ or

$$ \mathbf{x} = \mathbf{M}^{-1}\mathbf{K}\mathbf{x} + \mathbf{M}^{-1}\mathbf{b} . $$

Thus a solution to $\mathbf{A}\mathbf{x}=\mathbf{b}$ is a fixed point of iteration $$ \mathbf{x}^{(t+1)} = \mathbf{M}^{-1}\mathbf{K}\mathbf{x}^{(t)} + \mathbf{M}^{-1}\mathbf{b} = \mathbf{R}\mathbf{x}^{(t)} + \mathbf{c} . $$

• Under a suitable choice of $\mathbf{R}$, i.e., splitting of $\mathbf{A}$, the sequence $\mathbf{x}^{(k)}$ generated by the above iteration converges to a solution $\mathbf{A}\mathbf{x}=\mathbf{b}$:

Let $\rho(\mathbf{R})=\max_{i=1,\dotsc,n}|\lambda_i(\mathbf{R})|$, where $\lambda_i(\mathbf{R})$ is the $i$th (complex) eigenvalue of $\mathbf{R}$. When $\mathbf{A}$ is invertible, the iteration $\mathbf{x}^{(t+1)}=\mathbf{R}\mathbf{x}^{(t)} + \mathbf{c}$ converges to $\mathbf{A}^{-1}\mathbf{b}$ for any $\mathbf{x}^{(0)}$ if and only if $\rho(\mathbf{R}) < 1$.

Review of vector norms¶

A norm $\|\cdot\|: \mathbb{R}^n \to \mathbb{R}$ is defined by the following properties:

1. $\|\mathbf{x}\| \ge 0$,
2. $\|\mathbf{x}\| = 0 \iff \mathbf{x} = \mathbf{0}$,
3. $\|c\mathbf{x}\| = |c|\|\mathbf{x}\|$ for all $c \in \mathbb{R}$,
4. $\|\mathbf{x} + \mathbf{y}\| \le \|\mathbf{x}\| + \|\mathbf{y}\|$.

Typicall norms are

• $\ell_2$ (Euclidean) norm: $\|\mathbf{x}\| = \sqrt{\sum_{i=1}^nx_i^2}$;
• $\ell_1$ norm: $\|\mathbf{x}\| = \sum_{i=1}^n|x_i|$;
• $\ell_{\infty}$ (Manhatan) norm: $\|\mathbf{x}\| = \max_{i=1,\dots,n}|x_i|$;

Matrix norms¶

• Matrix $\mathbf{A} \in \mathbb{R}^{n\times n}$ can be considered as a vector in $\mathbb{R}^{n^2}$.
• However, it is convinient if a matrix norm is compatible with matrix multiplication.
• In addition to the defining properties of a norm above, we require

5. $\|\mathbf{A}\mathbf{B}\| \le \|\mathbf{A}\|\|\mathbf{B}\|$.

Typical matrix norms are

• Frobenius norm: $\|\mathbf{A}\|_F = \sqrt{\sum_{i,j=1}^n a_{ij}^2} = \sqrt{\text{trace}(\mathbf{A}\mathbf{A}^T)}$;
• Operator norm (induced by a vector norm $\|\cdot\|$): $\|\mathbf{A}\| = \sup_{\mathbf{y}\neq\mathbf{0}}\frac{\|\mathbf{A}\mathbf{y}\|}{\|\mathbf{y}\|}$.

It can be shown that

• $\|\mathbf{A}\|_1 = \max_{j=1,\dotsc,n}\sum_{i=1}^n|a_{ij}|$;
• $\|\mathbf{A}\|_{\infty} = \max_{i=1,\dotsc,n}\sum_{j=1}^n|a_{ij}|$;
• $\|\mathbf{A}\|_2 = \sqrt{\rho(\mathbf{A}^T\mathbf{A})}$.

Convergence of iterative methods¶

• Let $\mathbf{x}^{\star}$ be a solution of $\mathbf{A}\mathbf{x} = \mathbf{b}$.
• Equivalently, $\mathbf{x}^{\star}$ satisfies $\mathbf{x}^{\star} = \mathbf{R}\mathbf{x}^{\star} + \mathbf{c}$.
• Subtracting this from $\mathbf{x}^{(t+1)} = \mathbf{R}\mathbf{x}^{(t)} + \mathbf{c}$, we have

$$ \mathbf{x}^{(t+1)} - \mathbf{x}^{\star} = \mathbf{R}(\mathbf{x}^{(t)} - \mathbf{x}^{\star}). $$

• Take a vector norm on both sides:

$$ \|\mathbf{x}^{(t+1)} - \mathbf{x}^{\star}\| = \|\mathbf{R}(\mathbf{x}^{(t)} - \mathbf{x}^{\star})\| \le \|\mathbf{R}\|\|\mathbf{x}^{(t)} - \mathbf{x}^{\star}\| $$

where $\|\mathbf{R}\|$ is the induced operator norm.

• Thus if $\|\mathbf{R}\| < 1$ for a certain (induced) norm, then $\mathbf{x}^{(t)} \to \mathbf{x}^{\star}$.

Theorem¶

The spectral radius $\rho(\mathbf{A})$ of a matrix $\mathbf{A}\in\mathbb{R}^{n\times n}$ satisfies

$$ \rho(\mathbf{A}) \le \|\mathbf{A}\| $$

for any operator norm. Furthermore, for any $\mathbf{A}\in\mathbb{R}^{n\times n}$ and $\epsilon > 0$, there is an operator norm $\|\cdot\|$ such that $\|\mathbf{A}\| \le \rho(\mathbf{A}) + \epsilon$.
In other words, $$ \rho(\mathbf{A}) = \inf_{\|\cdot\|: \text{operator norm}} \|\mathbf{A}\|. $$

Thus it is immediate to see

$$ \rho(\mathbf{A}) < 1 \iff \|\mathbf{A}\| < 1 $$

for some operator norm.

Proof¶

If $\lambda$ is an eigenvalue of $\mathbf{A}$ with nonzero eigenvector $\mathbf{v}$, then $$ \|\mathbf{A}\mathbf{v}\| = |\lambda|\|\mathbf{v}\| $$ (for a vector norm). So $$ |\lambda| = \frac{\|\mathbf{A}\mathbf{v}\|}{\|\mathbf{v}\|} \le \|\mathbf{A}\|, $$ implying the first inequality.

For the second part, suppose $\mathbf{A}\in\mathbb{R}^{n\times n}$ and $\epsilon > 0$ are given. Then there exists an (complex) upper triangular matrix $\mathbf{T}$ and an invertible matrix $\mathbf{S}$ such that $$ \mathbf{A} = \mathbf{S}\mathbf{T}\mathbf{S}^{-1} $$ and the eigenvalues of $\mathbf{A}$ coincides with the diagonal entries of $\mathbf{T}$. (Schur decomposition).

For $\delta > 0$ consider a diagonal matrix $\mathbf{D}(\delta)=\text{diag}(1, \delta, \delta^2, \dotsc, \delta^{n-1})$, which is invertible. Then

$$ \mathbf{T}(\delta) \triangleq \mathbf{D}(\delta)^{-1}\mathbf{T}\mathbf{D}(\delta) =\mathbf{D}(\delta)^{-1}\mathbf{S}^{-1}\mathbf{A}\mathbf{S}\mathbf{D}(\delta) = (\mathbf{S}\mathbf{D}(\delta))^{-1}\mathbf{A}(\mathbf{S}\mathbf{D}(\delta)) $$

is an upper triangular matrix with entries $(\delta^{j-i}t_{ij})$ for $j \ge i$. So the off-diagonal entries tends to 0 as $\delta \to 0$.

Check $$ \|\mathbf{x}\|_{\delta} := \|(\mathbf{S}\mathbf{D}(\delta))^{-1}\mathbf{x}\|_{\infty} $$ defines a vector norm, which induces

$$ \begin{split} \|\mathbf{A}\|_{\delta} &\triangleq \sup_{\mathbf{x}\neq\mathbf{0}}\frac{\|\mathbf{A}\mathbf{x}\|_{\delta}}{\|\mathbf{x}\|_{\delta}} = \sup_{\mathbf{x}\neq\mathbf{0}}\frac{\|[\mathbf{S}\mathbf{D}(\delta)]^{-1}\mathbf{A}\mathbf{x}\|_{\infty}}{\|[\mathbf{S}\mathbf{D}(\delta)]^{-1}\mathbf{x}\|_{\infty}} \\ &= \|(\mathbf{S}\mathbf{D}(\delta))^{-1}\mathbf{A}(\mathbf{S}\mathbf{D}(\delta))\|_{\infty} = \|\mathbf{T}(\delta)\|_{\infty} = \max_{i=1,\dotsc,n}\sum_{j=i}^n |t_{ij}|\delta^{j-i}. \end{split} $$

Since for $\mathbf{y} = [\mathbf{S}\mathbf{D}(\delta)]^{-1}\mathbf{x}$, there holds $\mathbf{x} = [\mathbf{S}\mathbf{D}(\delta)]\mathbf{y}$ and
$$ \sup_{\mathbf{x}\neq\mathbf{0}}\frac{\|[\mathbf{S}\mathbf{D}(\delta)]^{-1}\mathbf{A}\mathbf{x}\|_{\infty}}{\|[\mathbf{S}\mathbf{D}(\delta)]^{-1}\mathbf{x}\|_{\infty}} = \sup_{\mathbf{y}\neq\mathbf{0}}\frac{\|[\mathbf{S}\mathbf{D}(\delta)]^{-1}\mathbf{A}[\mathbf{S}\mathbf{D}(\delta)]\mathbf{y}\|_{\infty}}{\|[\mathbf{S}\mathbf{D}(\delta)]^{-1}[\mathbf{S}\mathbf{D}(\delta)]\mathbf{y}\|_{\infty}} = \sup_{\mathbf{y}\neq\mathbf{0}}\frac{\|[\mathbf{S}\mathbf{D}(\delta)]^{-1}\mathbf{A}[\mathbf{S}\mathbf{D}(\delta)]\mathbf{y}\|_{\infty}}{\|\mathbf{y}\|_{\infty}} $$

Now since the eigenvalues of $\mathbf{A}$ coincides with $t_{ii}$, for each $\epsilon>0$ we can take a sufficiently small $\delta > 0$ so that $$ \max_{i=1,\dotsc,n}\sum_{j=i}^n |t_{ij}|\delta^{j-i} \le \rho(\mathbf{A}) + \epsilon. $$ This implies $\|\mathbf{A}\|_{\delta} \le \rho(\mathbf{A}) + \epsilon$.

Implications¶

• Recall

Let $\rho(\mathbf{R})=\max_{i=1,\dotsc,n}|\lambda_i(\mathbf{R})|$, where $\lambda_i(\mathbf{R})$ is the $i$th (complex) eigenvalue of $\mathbf{R}$. When $\mathbf{A}$ is invertible, the iteration $\mathbf{x}^{(t+1)}=\mathbf{R}\mathbf{x}^{(t)} + \mathbf{c}$ converges to $\mathbf{A}^{-1}\mathbf{b}$ for any $\mathbf{x}^{(0)}$ if and only if $\rho(\mathbf{R}) < 1$.

• The if part is proved using the above Theorem. This part holds even if $\mathbf{A}$ is singular; the limit may depend on $\mathbf{x}^{(0)}$, but it is always a solution to $\mathbf{A}\mathbf{x} = \mathbf{b}$.

• The only if part when $\mathbf{A}$ is inverible (hence $\mathbf{x}^{\star}$ is unique):

$$ \mathbf{x}^{(t)} - \mathbf{x}^{\star} = \mathbf{R}^t(\mathbf{x}^{(0)} - \mathbf{x}^{\star}). $$
If LHS converges to zero for any $\mathbf{x}^{(0)}$, then $\mathbf{R}^t \to \mathbf{0}$ as $t \to \infty$. This cannot occur if $|\lambda_i(\mathbf{R})| \ge 1$ for some $i$: if $\mathbf{x}^{(0)} = \mathbf{v}_i + \mathbf{x}^{\star}$ for an eigenvector $\mathbf{v}_i \neq \mathbf{0}$ such that $\mathbf{R}\mathbf{v}_i = \lambda_i\mathbf{v}_i$, then $\| R^t(\mathbf{x}^{(0)} - \mathbf{x}^{\star}) \| = |\lambda_i|^t\|\mathbf{v}_i\| \geq \|\mathbf{v}_i\| \neq 0$. + Invertibility is necessary since otherwise we do not know if $\mathbf{x}^{(t)}$ converges to a unique point.

Jacobi's method¶

$$ x_i^{(t+1)} = \frac{b_i - \sum_{j=1}^{i-1} a_{ij} x_j^{(t)} - \sum_{j=i+1}^n a_{ij} x_j^{(t)}}{a_{ii}}. $$

• Split $\mathbf{A} = \mathbf{L} + \mathbf{D} + \mathbf{U}$ = (strictly lower triangular) + (diagonal) + (strictly upper triangular).

• Take $\mathbf{M}=\mathbf{D}$ (easy to invert!) and $\mathbf{K}=-(\mathbf{L} + \mathbf{U})$:

$$ \mathbf{D} \mathbf{x}^{(t+1)} = - (\mathbf{L} + \mathbf{U}) \mathbf{x}^{(t)} + \mathbf{b}, $$

i.e., $$ \mathbf{x}^{(t+1)} = - \mathbf{D}^{-1} (\mathbf{L} + \mathbf{U}) \mathbf{x}^{(t)} + \mathbf{D}^{-1} \mathbf{b} = - \mathbf{D}^{-1} \mathbf{A} \mathbf{x}^{(t)} + \mathbf{x}^{(t)} + \mathbf{D}^{-1} \mathbf{b}. $$

• Convergence is guaranteed if $\mathbf{A}$ is striclty row diagonally dominant: $|a_{ii}| > \sum_{j\neq i}|a_{ij}|$.

• One round costs $2n^2$ flops with an unstructured $\mathbf{A}$. Gain over GE/LU if converges in $o(n)$ iterations.

• Saving is huge for sparse or structured $\mathbf{A}$. By structured, we mean the matrix-vector multiplication $\mathbf{A} \mathbf{v}$ is fast ($O(n)$ or $O(n \log n)$).

  • Often the multiplication is implicit and $\mathbf{A}$ is not even stored, e.g., finite difference: $(\mathbf{A}\mathbf{v})_i = v_i - v_{i+1}$.

Gauss-Seidel method¶

$$ x_i^{(t+1)} = \frac{b_i - \sum_{j=1}^{i-1} a_{ij} x_j^{(t+1)} - \sum_{j=i+1}^n a_{ij} x_j^{(t)}}{a_{ii}}. $$

• Split $\mathbf{A} = \mathbf{L} + \mathbf{D} + \mathbf{U}$ = (strictly lower triangular) + (diagonal) + (strictly upper triangular) as Jacobi.

• Take $\mathbf{M}=\mathbf{D}+\mathbf{L}$ (easy to invert, why?) and $\mathbf{K}=-\mathbf{U}$:

$$ (\mathbf{D} + \mathbf{L}) \mathbf{x}^{(t+1)} = - \mathbf{U} \mathbf{x}^{(t)} + \mathbf{b} $$

i.e., $$ \mathbf{x}^{(t+1)} = - (\mathbf{D} + \mathbf{L})^{-1} \mathbf{U} \mathbf{x}^{(t)} + (\mathbf{D} + \mathbf{L})^{-1} \mathbf{b}. $$

• Equivalent to

$$ \mathbf{D}\mathbf{x}^{(t+1)} = - \mathbf{L} \mathbf{x}^{(t+1)} - \mathbf{U} \mathbf{x}^{(t)} + \mathbf{b} $$

or $$ \mathbf{x}^{(t+1)} = \mathbf{D}^{-1}(- \mathbf{L} \mathbf{x}^{(t+1)} - \mathbf{U} \mathbf{x}^{(t)} + \mathbf{b}) $$ leading to the iteration.

• "Coordinate descent" version of Jacobi.

• Convergence is guaranteed if $\mathbf{A}$ is striclty row diagonally dominant.

Successive over-relaxation (SOR)¶

$$ x_i^{(t+1)} = \frac{\omega}{a_{ii}} \left( b_i - \sum_{j=1}^{i-1} a_{ij} x_j^{(t+1)} - \sum_{j=i+1}^n a_{ij} x_j^{(t)} \right)+ (1-\omega) x_i^{(t)}, $$

• $\omega=1$: Gauss-Seidel; $\omega \in (0, 1)$: underrelaxation; $\omega > 1$: overrelaxation

  • Relaxation in hope of faster convergence

• Split $\mathbf{A} = \mathbf{L} + \mathbf{D} + \mathbf{U}$ = (strictly lower triangular) + (diagonal) + (strictly upper triangular) as before.

• Take $\mathbf{M}=\frac{1}{\omega}\mathbf{D}+\mathbf{L}$ (easy to invert, why?) and $\mathbf{K}=\frac{1-\omega}{\omega}\mathbf{D}-\mathbf{U}$:

$$ \begin{split} (\mathbf{D} + \omega \mathbf{L})\mathbf{x}^{(t+1)} &= [(1-\omega) \mathbf{D} - \omega \mathbf{U}] \mathbf{x}^{(t)} + \omega \mathbf{b} \\ \mathbf{D}\mathbf{x}^{(t+1)} &= (1-\omega) \mathbf{D}\mathbf{x}^{(t)} + \omega ( -\mathbf{U}\mathbf{x}^{(t)} - \mathbf{L}\mathbf{x}^{(t+1)} + \mathbf{b} ) \\ \mathbf{x}^{(t+1)} &= (1-\omega)\mathbf{x}^{(t)} + \omega \mathbf{D}^{-1} ( -\mathbf{U}\mathbf{x}^{(t)} - \mathbf{L}\mathbf{x}^{(t+1)} + \mathbf{b} ) \end{split} $$

Conjugate gradient method¶

• Conjugate gradient and its variants are the top-notch iterative methods for solving huge, structured linear systems.

• Key idea: solving $\mathbf{A} \mathbf{x} = \mathbf{b}$ is equivalent to minimizing the quadratic function $\frac{1}{2} \mathbf{x}^T \mathbf{A} \mathbf{x} - \mathbf{b}^T \mathbf{x}$ if $\mathbf{A}$ is positive definite.

  Application to a fusion problem in physics:

Method	Number of Iterations
Gauss-Seidel	208,000
Block SOR methods	765
Incomplete Cholesky conjugate gradient	25

• We defer the details of CG to the graduate-level Advanced Statistical Computing course.

Numerical examples¶

The Rlinsolve package implements most commonly used iterative solvers.

Generate test matrix¶

Poisson matrix is a block tridiagonal matrix from (discretized) Poisson's equation $\nabla^2\psi = f$ in on the plane (with a certain boundary condition). This matrix is sparse, symmetric positive definite and has known eigenvalues.

Reference: G. H. Golub and C. F. Van Loan, Matrix Computations, second edition, Johns Hopkins University Press, Baltimore, Maryland, 1989 (Section 4.5.4).

Matrix-vector muliplication¶

Dense solve via Cholesky¶

Jacobi solver¶

It seems that Jacobi solver doesn't give the correct answer.

Documentation reveals that the default value of maxiter is 1000. A couple trial runs shows that 5000 Jacobi iterations are required to get an "accurate enough" solution.

Gauss-Seidel¶

SOR¶

Conjugate Gradient¶

• A basic tenet in numerical analysis:

The structure should be exploited whenever possible in solving a problem.