sessionInfo()
R version 4.2.2 (2022-10-31) Platform: x86_64-apple-darwin17.0 (64-bit) Running under: macOS Catalina 10.15.7 Matrix products: default BLAS: /Library/Frameworks/R.framework/Versions/4.2/Resources/lib/libRblas.0.dylib LAPACK: /Library/Frameworks/R.framework/Versions/4.2/Resources/lib/libRlapack.dylib locale: [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8 attached base packages: [1] stats graphics grDevices utils datasets methods base loaded via a namespace (and not attached): [1] fansi_1.0.4 crayon_1.5.2 digest_0.6.31 utf8_1.2.2 [5] IRdisplay_1.1 repr_1.1.5 lifecycle_1.0.3 jsonlite_1.8.4 [9] evaluate_0.20 pillar_1.8.1 rlang_1.0.6 cli_3.6.0 [13] uuid_1.1-0 vctrs_0.5.2 IRkernel_1.3.2 tools_4.2.2 [17] glue_1.6.2 fastmap_1.1.0 compiler_4.2.2 base64enc_0.1-3 [21] pbdZMQ_0.3-9 htmltools_0.5.4
Golden section search¶
$d=1$.
Applicable to functions defined on an interval of the real line.
Assumption: $f$ is continuous and strictly unimodal on the interval
\
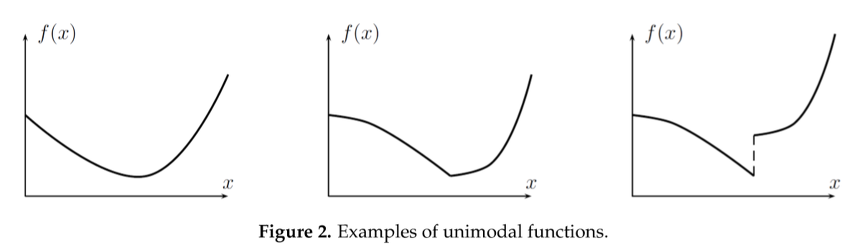
A function $f: [a,b] \to \mathbb{R}$ is strictly unimodal if
$$
f(\lambda x + (1-\lambda) y) < \max\{ f(x), f(y) \},
\quad
x, y \in [a, b],~x\neq y, ~\lambda \in (0, 1).
$$
Idea: keep track of three points $a < x_1 < b$ such that $f(x_1) < \min\{f(a), f(b)\}$
Choose a new point $x_0$ such that $x_0$ belongs to the longer of intervals $(a, x_1)$ and $(x_1, b)$.
WLOG, suppose $a < x_0 < x_1$.
- If $f(x_0) > f(x_1)$, then the minimum lies in the interval $(x_0, b)$. Hence set $(a, x_1, b) := (x_0, x_1, b)$.
- Otherwise, the minimum lies in the interval $(a, x_1)$. Hence set $(a, x_1, b) := (a, x_0, x_1)$.

Above rules do not say how to choose $x_0$. A possibility is to keep the lengths of the two possible candidate intervals the same: $b - x_0 = x_1 - a$, and the relative position of the intermediate points ($x_1$ to $(x_0, b)$; $x_0$ to $(a, x_1)$) the same.
Let $\alpha = \frac{x_0 - a}{b - a}$ and $y = \frac{x_1 - x_0}{b -a}$. Then we require $\frac{b - x_1}{b - a} = \alpha$ and
By solving this equation, we have $\alpha = \frac{3 - \sqrt{5}}{2}$ or $1 - \alpha = \frac{\sqrt{5} - 1}{2}$, the golden section.
goldensection <- function(f, a, b, tol=1e-6) {
alpha <- (3 - sqrt(5)) * 0.5
f
iter <- 0
while ( b - a > tol ) {
x0 <- a + alpha * (b - a)
x1 <- b - alpha * (b - a)
print(c(a, x1, b))
if ( f(x0) > f(x1) ) {
a <- x0
} else { # if ( f(x0) < f(x1) ) {
b <- x1
x1 <- x0
} #else {
# if ( f(b) < f(a) ) {
# a <- x0
# } else {
# b <- x1
# x1 <- x0
# }
#}
iter <- iter + 1
}
ret <- list(val = (a + b) / 2, iter = iter)
}
# binomial log-likelihood of 7 successes and 3 failures
F <- function(x) { -7 * log(x) - 3 * log(1 - x) }
goldensection(F, 0.01, 0.99, tol=1e-8)
[1] 0.0100000 0.6156733 0.9900000 [1] 0.3843267 0.7586534 0.9900000 [1] 0.6156733 0.8470199 0.9900000 [1] 0.6156733 0.7586534 0.8470199 [1] 0.6156733 0.7040399 0.7586534 [1] 0.6702868 0.7249004 0.7586534 [1] 0.6702868 0.7040399 0.7249004 [1] 0.6911473 0.7120079 0.7249004 [1] 0.6911473 0.7040399 0.7120079 [1] 0.6911473 0.6991154 0.7040399 [1] 0.6960718 0.7009963 0.7040399 [1] 0.6960718 0.6991154 0.7009963 [1] 0.6979528 0.6998338 0.7009963 [1] 0.6991154 0.7002779 0.7009963 [1] 0.6991154 0.6998338 0.7002779 [1] 0.6995594 0.7000034 0.7002779 [1] 0.6998338 0.7001083 0.7002779 [1] 0.6998338 0.7000034 0.7001083 [1] 0.6999387 0.7000435 0.7001083 [1] 0.6999387 0.7000034 0.7000435 [1] 0.6999787 0.7000187 0.7000435 [1] 0.6999787 0.7000034 0.7000187 [1] 0.6999940 0.7000093 0.7000187 [1] 0.6999940 0.7000034 0.7000093 [1] 0.6999940 0.6999998 0.7000034 [1] 0.6999976 0.7000012 0.7000034 [1] 0.6999976 0.6999998 0.7000012 [1] 0.6999990 0.7000004 0.7000012 [1] 0.6999990 0.6999998 0.7000004 [1] 0.6999995 0.7000000 0.7000004 [1] 0.6999998 0.7000002 0.7000004 [1] 0.6999998 0.7000000 0.7000002 [1] 0.7000000 0.7000001 0.7000002 [1] 0.7000000 0.7000000 0.7000001 [1] 0.7 0.7 0.7 [1] 0.7 0.7 0.7 [1] 0.7 0.7 0.7 [1] 0.7 0.7 0.7 [1] 0.7 0.7 0.7
Convergence of golden section search is slow but sure to find the global minimum (if the assumptions are met).
Newton's Method¶
- First-order optimality condition
Apply Newton-Raphson to $g(\mathbf{x})=\nabla f(\mathbf{x})$.
Idea: iterative quadratic approximation.
Second-order Taylor expansion of the objective function around the current iterate $\mathbf{x}^{(t)}$
and then minimize the quadratic approximation.
- To maximize the quadratic appriximation function, we equate its gradient to zero
which suggests the next iterate $$ \begin{eqnarray*} \mathbf{x}^{(t+1)} &=& \mathbf{x}^{(t)} - [\nabla^2 f(\mathbf{x}^{(t)})]^{-1} \nabla f(\mathbf{x}^{(t)}), \end{eqnarray*} $$ a complete analogue of the univariate Newton-Raphson for solving $g(x)=0$.
- Considered the gold standard for its fast (quadratic) convergence: $\mathbf{x}^{(t)} \to \mathbf{x}^{\star}$ and
In words, the estimate gets accurate by two decimal digits per iteration.
We call this naive Newton's method.
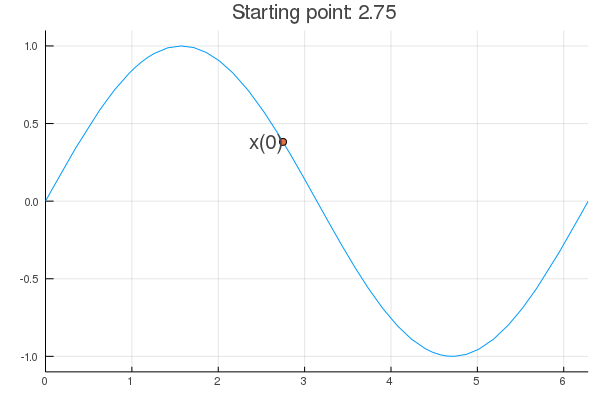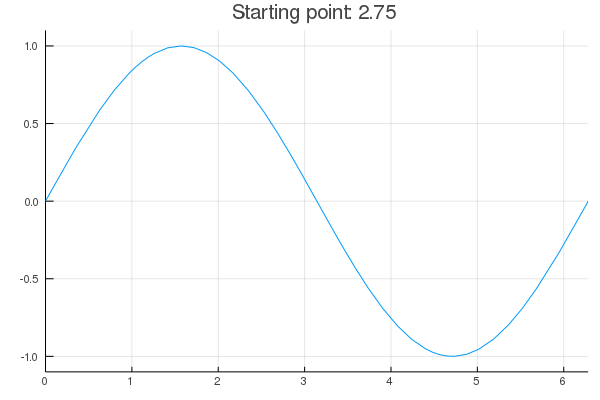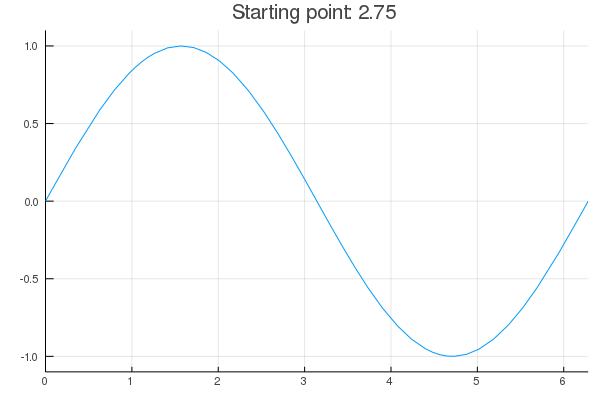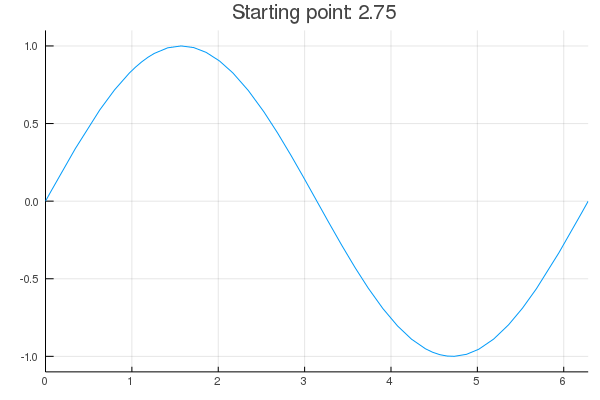
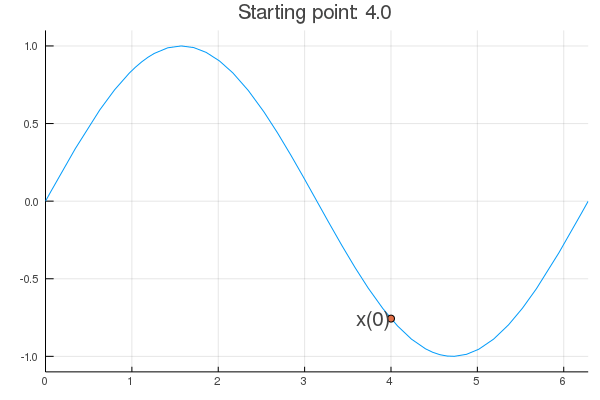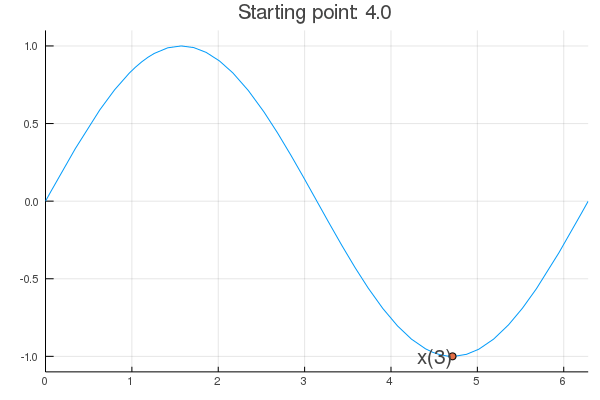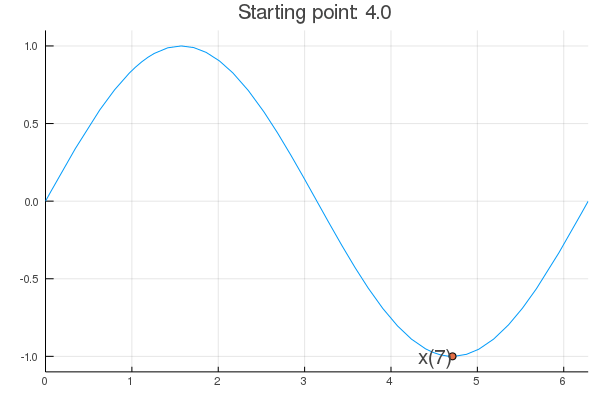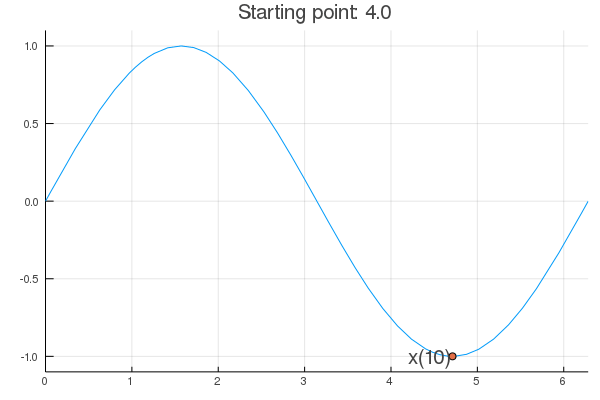
- Stability issue: naive Newton's iterate is not guaranteed to be a descent algorithm, i.e., that ensures $f(\mathbf{x}^{(t+1)}) \le f(\mathbf{x}^{(t)})$. It's equally happy to head uphill or downhill. Following example shows that the Newton iterate converges to a local maximum, converges to a local minimum, or diverges depending on starting points.
purenewton <- function(f, df, d2f, x0, maxiter=10, tol=1e-6) {
xold <- x0
stop <- FALSE
iter <- 1
x <- x0
while ((!stop) && (iter < maxiter)) {
x <- x - df(x) / d2f(x)
print(x)
xdiff <- x - xold
if (abs(xdiff) < tol) stop <- TRUE
xold <- x
iter <- iter + 1
}
return(list(val=x, iter=iter))
}
f <- function(x) sin(x) # objective function
df <- function(x) cos(x) # gradient
d2f <- function(x) -sin(x) # hessian
purenewton(f, df, d2f, 2.0)
[1] 1.542342 [1] 1.570804 [1] 1.570796 [1] 1.570796
- $val
- 1.5707963267949
- $iter
- 5
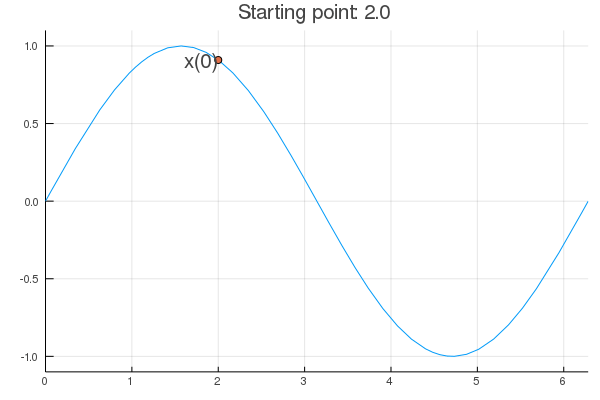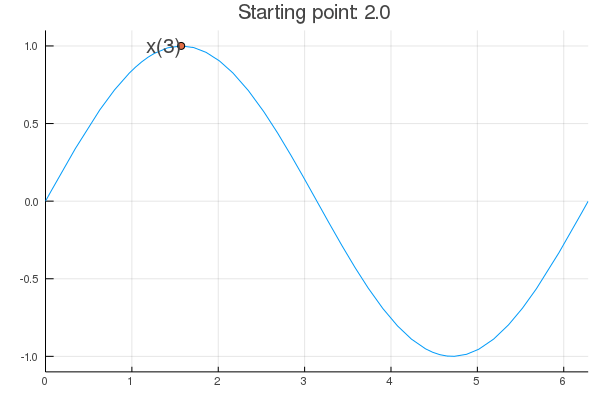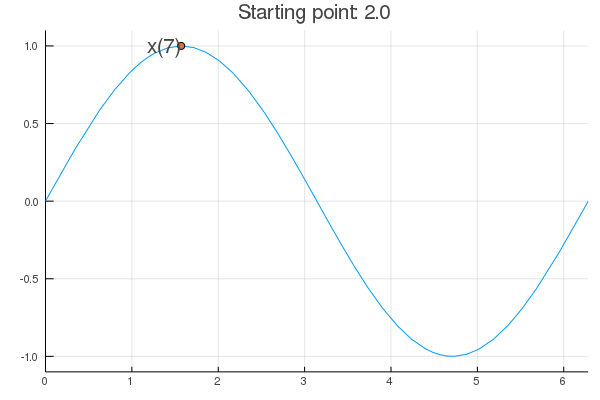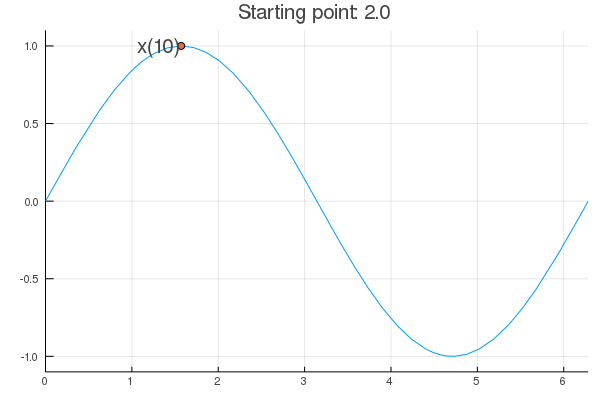
purenewton(f, df, d2f, 2.75)
[1] 0.328211 [1] 3.264834 [1] 11.33789 [1] 10.98155 [1] 10.99558 [1] 10.99557
- $val
- 10.9955742875643
- $iter
- 7
purenewton(f, df, d2f, 4.0)
[1] 4.863691 [1] 4.711224 [1] 4.712389 [1] 4.712389
- $val
- 4.71238898038469
- $iter
- 5
Practical Newton¶
A remedy for the instability issue:
- approximate $\nabla^2 f(\mathbf{x}^{(t)})$ by a positive definite $\mathbf{H}^{(t)}$ (if it's not), and
- line search (backtracking) to ensure the descent property.
Why insist on a positive definite approximation of Hessian? First define the Newton direction:
By first-order Taylor expansion,
$$
\begin{align*}
f(\mathbf{x}^{(t)} + s \Delta \mathbf{x}^{(t)}) - f(\mathbf{x}^{(t)})
&= \nabla f(\mathbf{x}^{(t)})^T s \Delta \mathbf{x}^{(t)} + o(s) \\
&= - s \cdot \nabla f(\mathbf{x}^{(t)})^T [\mathbf{H}^{(t)}]^{-1} \nabla f(\mathbf{x}^{(t)}) + o(s).
\end{align*}
$$
For $s$ sufficiently small, $f(\mathbf{x}^{(t)} + s \Delta \mathbf{x}^{(t)}) - f(\mathbf{x}^{(t)})$ is strictly negative if $\mathbf{H}^{(t)}$ is positive definite.
The quantity $\{\nabla f(\mathbf{x}^{(t)})^T [\mathbf{H}^{(t)}]^{-1} \nabla f(\mathbf{x}^{(t)})\}^{1/2}$ is termed the Newton decrement.
- In summary, a practical Newton-type algorithm iterates according to
where $\mathbf{H}^{(t)}$ is a positive definite approximation to $\nabla^2 f(\mathbf{x}^{(t)})$ and $s$ is a step size.
- For strictly convex $f$, $\nabla^2 f(\mathbf{x}^{(t)})$ is always positive definite. In this case, the above algorithm is called damped Newton. However, line search is still needed (at least for a finite number of times) to guarantee convergence.
Line search¶
Line search: compute the Newton direction and search $s$ such that $f(\mathbf{x}^{(t)} + s \Delta \mathbf{x}^{(t)})$ is minimized.
Note the Newton direction only needs to be calculated once. Cost of line search mainly lies in objective function evaluation.
Full line search: $s = \arg\min_{\alpha} f(\mathbf{x}^{(t)} + \alpha \Delta \mathbf{x}^{(t)})$. May use golden section search.
Approximate line search: step-halving ($s=1,1/2,\ldots$), Amijo rule, ...
Backtracking line search (Armijo rule)
# Backtracking line search
# given: descent direction ∆x, x ∈ domf, α ∈ (0,0.5), β ∈ (0,1).
t <- 1.0
while (f(x + t * delx) > f(x) + alpha * t * sum(gradf(x) * delx) {
t <- beta * t
}
The lower dashed line shows the linear extrapolation of $f$, and the upper dashed line has a slope a factor of α smaller. The backtracking condition is that $f$ lies below the upper dashed line, i.e., $0 \le t \le t_0$.
How to approximate $\nabla^2 f(\mathbf{x})$? More of an art than science. Often requires problem specific analysis.
Taking $\mathbf{H}^{(t)} = \mathbf{I}$ leads to the gradient descent method (see below).
Fisher scoring¶
Consider MLE in which $f(\mathbf{x}) = -\ell(\boldsymbol{\theta})$, where $\ell(\boldsymbol{\theta})$ is the log-likelihood of parameter $\boldsymbol{\theta}$.
Fisher scoring method: replace $- \nabla^2 \ell(\boldsymbol{\theta})$ by the expected Fisher information matrix
which is true under exchangeability of tne expectation and the differentiation (true for most common distributions).
Therefore we set $\mathbf{H}^{(t)}=\mathbf{I}(\boldsymbol{\theta}^{(t)})$ and obtain the Fisher scoring algorithm:
- Combined with line search, a descent algorithm can be devised.
Example: logistic regression¶
Binary data: response $y_i \in \{0,1\}$, predictor $\mathbf{x}_i \in \mathbb{R}^{p}$.
Model: $y_i \sim $Bernoulli$(p_i)$, where
- MLE: density
- Log likelihood of the data $(y_i,\mathbf{x}_i)$, $i=1,\ldots,n$, and its derivatives are
(why the last line?)
- Therefore for this problem Newton's method == Fisher scoring:
where $$ \mathbf{z}^{(t)} = \mathbf{X} \beta^{(t)} + s[\mathbf{W}^{(t)}]^{-1} (\mathbf{y} - \mathbf{p}^{(t)}) $$ are the working responses. A Newton iteration is equivalent to solving a weighed least squares problem $$ \min_{\beta} \sum_{i=1}^n w_i (z_i - \mathbf{x}_i^T \beta)^2 $$ for which we know how to solve well. Thus the name IRLS (iteratively re-weighted least squares).
- Implication: if a weighted least squares solver is at hand, then logistic regression models can be fitted.
- IRLS == Fisher scoring == Newton's method
Example: Poisson regression¶
Count data: response $y_i \in \{0, 1, 2, \dotsc \}$, predictor $\mathbf{x}_i \in \mathbb{R}^{p}$.
Model: $y_i \sim $Poisson$(\lambda_i)$, where
- MLE: density
- Log likelihood of the data $(y_i,\mathbf{x}_i)$, $i=1,\ldots,n$, and its derivatives are
(why the last line?)
- Therefore for this problem Newton's method == Fisher scoring:
where $$ \mathbf{z}^{(t)} = \mathbf{X} \beta^{(t)} + s[\mathbf{W}^{(t)}]^{-1} (\mathbf{y} - \boldsymbol{\lambda}^{(t)}) $$ are the working responses. A Newton iteration is again equivalent to solving a weighed least squares problem $$ \min_{\beta} \sum_{i=1}^n w_i (z_i - \mathbf{x}_i^T \beta)^2 $$ which leads to the IRLS.
- Implication: if a weighted least squares solver is at hand, then Poisson regression models can be fitted.
- IRLS == Fisher scoring == Newton's method
# Quarterly count of AIDS deaths in Australia (from Dobson, 1990)
deaths <- c(0, 1, 2, 3, 1, 4, 9, 18, 23, 31, 20, 25, 37, 45)
(quarters <- seq_along(deaths))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
# Poisson regression using Fisher scoring (IRLS) and step halving
# Model: lambda = exp(beta0 + beta1 * quarter), or deaths ~ quarter
poissonreg <- function(x, y, maxiter=10, tol=1e-6) {
beta0 <- matrix(0, nrow=2, ncol=1) # initial point
betaold <- beta0
stop <- FALSE
iter <- 1
inneriter <- rep(0, maxiter) # to count no. step halving
beta <- beta0
lik <- function(bet) {eta <- bet[1] + bet[2] * x; sum( y * eta - exp(eta) ) } # log-likelihood
likold <- lik(betaold)
while ((!stop) && (iter < maxiter)) {
eta <- beta[1] + x * beta[2]
w <- exp(eta) # lambda
# line search by step halving
s <- 1.0
for (i in 1:5) {
z <- eta + s * (y / w - 1) # working response
m <- lm(z ~ x, weights=w) # weighted least squares
beta <- as.matrix(coef(m))
curlik <- lik(beta)
if (curlik > likold) break
s <- s * 0.5
inneriter[iter] <- inneriter[iter] + 1
}
print(c(as.numeric(beta), inneriter[iter], curlik))
betadiff <- beta - betaold
if (norm(betadiff, "F") < tol) stop <- TRUE
likold <- curlik
betaold <- beta
iter <- iter + 1
}
return(list(val=as.numeric(beta), iter=iter, inneriter=inneriter[1:iter]))
}
poissonreg(quarters, deaths)
[1] -1.3076923 0.4184066 3.0000000 443.4763188 [1] 0.6456032 0.2401380 0.0000000 469.9257845 [1] 0.3743785 0.2541525 0.0000000 472.0483495 [1] 0.3400344 0.2564929 0.0000000 472.0625465 [1] 0.3396340 0.2565236 0.0000000 472.0625479 [1] 0.3396339 0.2565236 0.0000000 472.0625479
- $val
-
- 0.339633920708135
- 0.256523593717915
- $iter
- 7
- $inneriter
-
- 3
- 0
- 0
- 0
- 0
- 0
- 0
m <- glm(deaths ~ quarters, family = poisson())
coef(m)
- (Intercept)
- 0.339633920708136
- quarters
- 0.256523593717915
Homework: repeat this using the Armijo rule.
Generalized Linear Models (GLM)¶
That IRLS == Fisher scoring == Newton's method for both logistic and Poisson regression is not a coincidence. Let's consider a more general class of generalized linear models (GLM).
Exponential families¶
- Random variable $Y$ belongs to an exponential family if the density
* $\eta$: natural parameter.
* $\phi>0$: dispersion parameter.
* Mean: $\mu= b'(\eta)$. When $b'(\cdot)$ is invertible, function $g(\cdot)=[b']^{-1}(\cdot)$ is called the canonical link function.
* Variance $\mathbf{Var}{Y}=b''(\eta)a(\phi)$.
- For example, if $Y \sim \text{Ber}(\mu)$, then
Hence $$ \eta = \log \frac{\mu}{1-\mu}, \quad \mu = \frac{e^{\eta}}{1+e^{\eta}}, \quad b(\eta) = -\log (1-\mu) = \log(1+e^{\eta}) $$ Hence $$ b'(\eta) = \frac{e^{\eta}}{1+e^{\eta}} = g^{-1}(\eta). $$ as above.
| Family | Canonical Link | Variance Function |
|---|---|---|
| Normal (unit variance) | $\eta=\mu$ | 1 |
| Poisson | $\eta=\log \mu$ | $\mu$ |
| Binomial | $\eta=\log \left(\frac{\mu}{1 - \mu} \right)$ | $\mu (1 - \mu)$ |
| Gamma | $\eta = \mu^{-1}$ | $\mu^2$ |
| Inverse Gaussian | $\eta = \mu^{-2}$ | $\mu^3$ |
Generalized linear models¶
GLM models the conditional distribution of $Y$ given predictors $\mathbf{x}$ through the conditional mean $\mu = \mathbf{E}(Y|\mathbf{x})$ via a strictly increasing link function $$ g(\mu) = \mathbf{x}^T \beta, \quad \mu = g^{-1}(\mathbf{x}^T\beta) = b'(\eta) $$
From these relations we have (assuming no overdispersion, i.e., $a(\phi)\equiv 1$) $$ \mathbf{x}^T d\beta = g'(\mu)d\mu, \quad d\mu = b''(\eta)d\eta, \quad b''(\eta) = \mathbf{Var}[Y] = \sigma^2, \quad d\eta = \frac{1}{b''(\eta)}d\mu = \frac{1}{b''(\eta)g'(\mu)}\mathbf{x}^T d\beta. $$ Therefore $$ d\mu = \frac{1}{g'(\mu)}\mathbf{x}^T d\beta . $$
Then, after some workout with matrix calculus, we have for $n$ samples:
- Score, Hessian, information
- Fisher scoring method:
IRLS with weights $w_i = [1/g'(\mu_i)]^2/\sigma_i^2$ and some working responses $z_i$.
For canonical link, $\mathbf{x}^T\beta = g(\mu) =[b']^{-1}(\mu) = \eta$. The second term of Hessian vanishes because $d\eta=\mathbf{x}^Td\beta$ and $b''(\eta)=1/g'(\mu)$. The Hessian coincides with Fisher information matrix. IRLS == Fisher scoring == Newton's method. Hence MLE is a convex optimization problem.
Non-canonical link, Fisher scoring != Newton's method, and MLE is in general a non-convex optimization problem.
Example: Probit regression (binary response with probit link).
where $\Phi(\cdot)$ is the cdf of a standard normal. Exceptionally, this problem is a convex optimization problem.
- R implements the Fisher scoring method, aka IRLS, for GLMs in function
glm().
Nonlinear regression - Gauss-Newton method¶
- Now we finally get to the problem Gauss faced in 1801!
Relocate the dwarf planet Ceres https://en.wikipedia.org/wiki/Ceres_(dwarf_planet) by fitting 24 observations to a 6-parameter (nonlinear) orbit. - In 1801, Jan 1 -- Feb 11 (41 days), astronomer Piazzi discovered Ceres, which was lost behind the Sun after observing its orbit 24 times. - Aug -- Sep, futile search by top astronomers; Laplace claimed it unsolvable. - Oct -- Nov, Gauss did calculations by method of least squares, sent his results to astronomer von Zach. - Dec 31, von Zach relocated Ceres according to Gauss’ calculation.
- Nonlinear least squares (curve fitting):
For example, $y_i =$ dry weight of onion and $x_i=$ growth time, and we want to fit a 3-parameter growth curve $$ \mu(x, \beta_1,\beta_2,\beta_3) = \frac{\beta_3}{1 + \exp(-\beta_1 - \beta_2 x)}. $$

If $\mu_i$ is a linear function of $\beta$, i.e., $\mathbf{x}_i^T\beta$, then NLLS reduces to the usual least squares.
"Score" and "information matrices"
where $\mathbf{J}(\beta)^T = [\nabla \mu_1(\mathbf{x}_1,\beta), \ldots, \nabla \mu_n(\mathbf{x}_n,\beta)] \in \mathbb{R}^{p \times n}$.
- Gauss-Newton (= "Fisher scoring method") uses $\mathbf{I}(\beta)$, which is always positive semidefinite.
- Justification
- Residuals $y_i - \mu_i(\mathbf{x}_i, \beta)$ are small, or $\mu_i$ is nearly linear;
- Model the data as $y_i \sim N(\mu_i(\mathbf{x}_i, \beta), \sigma^2)$, where $\sigma^2$ is assumed to be known. Then,
Thus
$$
\mathbf{E}[-\nabla^2 \ell(\beta)] = \sum_{i=1}^n \nabla \mu_i(\beta) \nabla \mu_i(\beta)^T.
$$
- In fact Gauss invented the Gaussian (normal) distribution to justify this method!
Gradient descent method¶
- Iteration:
for some step size $\gamma_t$. This is a special case of the Netwon-type algorithms with $\mathbf{H}_t = \mathbf{I}$ and $\Delta\mathbf{x} = \nabla f(\mathbf{x}^{(t)})$.
- Idea: iterative linear approximation (first-order Taylor series expansion).
and then minimize the linear approximation within a compact set: let $\Delta\mathbf{x} = \mathbf{x}^{(t+1)}-\mathbf{x}^{(t)}$ to choose. Solve $$ \min_{\|\Delta\mathbf{x}\|_2 \le 1} \nabla f(\mathbf{x}^{(t)})^T\Delta\mathbf{x} $$ to obtain $\Delta\mathbf{x} = -\nabla f(\mathbf{x}^{(t)})/\|\nabla f(\mathbf{x}^{(t)})\|_2 \propto -\nabla f(\mathbf{x}^{(t)})$.
Step sizes are chosen so that the descent property is maintained (e.g., line search).
- Step size must be chosen at any time, since unlike Netwon's method, first-order approximation is always unbounded below.
Pros
- Each iteration is inexpensive.
- No need to derive, compute, store and invert Hessians; attractive in large scale problems.
Cons
- Slow convergence (zigzagging).
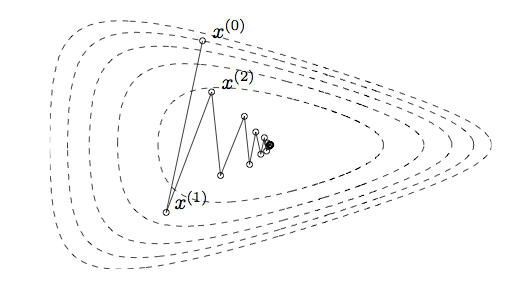
- Do not work for non-smooth problems.
Convergence¶
If
- $f$ is convex and differentiable over $\mathbb{R}^d$;
- $f$ has $L$-Lipschitz gradients, i.e., $\|\nabla f(\mathbf{x}) - \nabla f(\mathbf{y})\|_2 \le L\|\mathbf{x} - \mathbf{y} \|_2$;
- $p^{\star} = \inf_{\mathbf{x}\in\mathbb{R}^d} f(x) > -\infty$ and attained at $\mathbf{x}^{\star}$,
then
for constant step size ($\gamma_t = \gamma \in (0, 1/L]$), a *sublinear* convergence. Similar upper bound with line search.
- In general, the best we can obtain from gradient descent is linear convergence (cf. quadratic convergence of Newton).
Examples¶
Least squares: $f(\beta) = \frac{1}{2}\|\mathbf{X}\beta - \mathbf{y}\|_2^2 = \frac{1}{2}\beta^T\mathbf{X}^T\mathbf{X}\beta - \beta^T\mathbf{X}^T\mathbf{y} + \frac{1}{2}\mathbf{y}^T\mathbf{y}$
- Gradient $\nabla f(\beta) = \mathbf{X}^T\mathbf{X}\beta - \mathbf{X}^T\mathbf{y}$ is $\|\mathbf{X}^T\mathbf{X}\|_2$-Lipschitz. Hence $\gamma \in (0, 1/\sigma_{\max}(\mathbf{X})^2]$ guarantees descent property and convergence.
Logistic regression: $f(\beta) = -\sum_{i=1}^n \left[ y_i \mathbf{x}_i^T \beta - \log (1 + e^{\mathbf{x}_i^T \beta}) \right]$
Gradient $\nabla f(\beta) = - \mathbf{X}^T (\mathbf{y} - \mathbf{p})$ is $\frac{1}{4}\|\mathbf{X}^T\mathbf{X}\|_2$-Lipschitz.
May be unbounded below, e.g., all the data are of the same class.
Adding a ridge penalty $\frac{\rho}{2}\|\beta\|_2^2$ makes the problem identifiable.
Poisson regression: $f(\beta) = -\sum_{i=1}^n \left[ y_i \mathbf{x}_i^T \beta - \exp(\mathbf{x}_i^T \beta) - \log(y_i!) \right]$
- Gradient
is *not* Lipschitz (HW). What is the consequence?
# Poisson regression using gradient descent
# Model: lambda = exp(beta0 + beta1 * quarter), or deaths ~ quarter
poissonreg_grad <- function(x, y, maxiter=10, tol=1e-6) {
beta0 <- matrix(0, nrow=2, ncol=1) # initial point
betaold <- beta0
iter <- 1
inneriter <- rep(0, maxiter) # to count no. step halving
betamat <- matrix(NA, nrow=maxiter, ncol=length(beta0) + 2)
colnames(betamat) <- c("beta0", "beta1", "inneriter", "lik")
beta <- beta0
lik <- function(bet) {eta <- bet[1] + bet[2] * x; sum( y * eta - exp(eta) ) } # log-likelihood
likold <- lik(betaold)
while (iter < maxiter) {
eta <- beta[1] + x * beta[2]
lam <- exp(eta) # lambda
grad <- as.matrix(c(sum(lam - y), sum((lam - y) * x)))
# line search by step halving
#s <- 0.00001
s <- 0.00005
for (i in 1:5) {
beta <- beta - s * grad
curlik <- lik(beta)
if (curlik > likold) break
s <- s * 0.5
inneriter[iter] <- inneriter[iter] + 1
}
#print(c(as.numeric(beta), inneriter[iter], curlik))
betamat[iter,] <- c(as.numeric(beta), inneriter[iter], curlik)
betadiff <- beta - betaold
if (norm(betadiff, "F") < tol) break
likold <- curlik
betaold <- beta
iter <- iter + 1
}
#return(list(val=as.numeric(beta), iter=iter, inneriter=inneriter[1:iter]))
return(betamat[1:iter,])
}
# Australian AIDS data from the IRLS example above
pm <- poissonreg_grad(quarters, deaths, tol=1e-8, maxiter=20000)
head(pm, 10)
tail(pm, 10)
| beta0 | beta1 | inneriter | lik |
|---|---|---|---|
| 0.01025000 | 0.1149500 | 0 | 241.3754 |
| 0.01933954 | 0.2178634 | 0 | 423.2101 |
| 0.02505110 | 0.2826001 | 0 | 471.3151 |
| 0.02532401 | 0.2830995 | 0 | 471.3176 |
| 0.02553404 | 0.2828481 | 0 | 471.3190 |
| 0.02577206 | 0.2829335 | 0 | 471.3201 |
| 0.02599725 | 0.2828674 | 0 | 471.3212 |
| 0.02622798 | 0.2828694 | 0 | 471.3222 |
| 0.02645600 | 0.2828408 | 0 | 471.3233 |
| 0.02668501 | 0.2828259 | 0 | 471.3243 |
| beta0 | beta1 | inneriter | lik | |
|---|---|---|---|---|
| [12951,] | 0.3396212 | 0.2565247 | 0 | 472.0625 |
| [12952,] | 0.3396212 | 0.2565247 | 0 | 472.0625 |
| [12953,] | 0.3396212 | 0.2565247 | 0 | 472.0625 |
| [12954,] | 0.3396212 | 0.2565247 | 0 | 472.0625 |
| [12955,] | 0.3396212 | 0.2565247 | 0 | 472.0625 |
| [12956,] | 0.3396212 | 0.2565247 | 0 | 472.0625 |
| [12957,] | 0.3396212 | 0.2565247 | 0 | 472.0625 |
| [12958,] | 0.3396213 | 0.2565247 | 0 | 472.0625 |
| [12959,] | 0.3396213 | 0.2565247 | 0 | 472.0625 |
| [12960,] | 0.3396213 | 0.2565247 | 0 | 472.0625 |
Recall
m <- glm(deaths ~ quarters, family = poisson())
coef(m)
- (Intercept)
- 0.339633920708136
- quarters
- 0.256523593717915
Coordinate descent¶
- Idea: coordinate-wise minimization is often easier than the full-dimensional minimization

Similar to the Gauss-Seidel method for solving linear equations.
Block descent: a vector version of coordinate descent
Q: why objective value converges?
- A: descent property
Caution: even if the objective function is convex, coordinate descent may not converge to the global minimum and converge to a suboptimal point.