Cholesky Decomposition¶

André-Louis Cholesky, 1875-1918.

• A basic tenet in numerical analysis:

The structure should be exploited whenever possible in solving a problem.

Common structures include: symmetry, positive (semi)definiteness, sparsity, Kronecker product, low rank, ...

• LU decomposition (Gaussian Elimination) is not used in statistics very often because most of time statisticians deal with positive (semi)definite matrices.

• Recall that a matrix $M$ is positive (semi)definite if

• Example: normal equation

for linear regression, the coefficient matrix $\mathbf{X}^T \mathbf{X}$ is symmetric and positive semidefinite. How to exploit this structure?

• Most of time statisticians deal with positive (semi)definite matrices.

Cholesky decomposition¶

• Theorem: Let $\mathbf{A} \in \mathbb{R}^{n \times n}$ be symmetric and positive definite. Then $\mathbf{A} = \mathbf{L} \mathbf{L}^T$, where $\mathbf{L}$ is lower triangular with positive diagonal entries and is unique.

Proof (by induction):
If $n=1$, then $0 < a = \sqrt{a}\sqrt{a}$. For $n>1$, the block equation $$ \begin{eqnarray*} \begin{bmatrix} a_{11} & \mathbf{a}^T \\ \mathbf{a} & \mathbf{A}_{22} \end{bmatrix} = \begin{bmatrix} \ell_{11} & \mathbf{0}_{n-1}^T \\ \mathbf{b} & \mathbf{L}_{22} \end{bmatrix} \begin{bmatrix} \ell_{11} & \mathbf{b}^T \\ \mathbf{0}_{n-1} & \mathbf{L}_{22}^T \end{bmatrix} \end{eqnarray*} $$ entails $$ \begin{eqnarray*} a_{11} &=& \ell_{11}^2 \\ \mathbf{a} &=& \ell_{11} \mathbf{b} \\ \mathbf{A}_{22} &=& \mathbf{b} \mathbf{b}^T + \mathbf{L}_{22} \mathbf{L}_{22}^T . \end{eqnarray*} $$
Since $a_{11}>0$ (why?), $\ell_{11}=\sqrt{a_{11}}$ and $\mathbf{b}=a_{11}^{-1/2}\mathbf{a}$ are uniquely determined. $\mathbf{A}_{22} - \mathbf{b} \mathbf{b}^T = \mathbf{A}_{22} - a_{11}^{-1} \mathbf{a} \mathbf{a}^T$ is positive definite of size $(n-1)\times(n-1)$ because $\mathbf{A}_{22}$ is positive definite (why? homework). By induction hypothesis, lower triangular $\mathbf{L}_{22}$ such that $\mathbf{A}_{22} - \mathbf{b} \mathbf{b}^T = \mathbf{L}_{22}^T\mathbf{L}_{22}$ exists and is unique.

• This proof is constructive and completely specifies the algorithm:

for k=1:n
    for j=k+1:n
        a_jk_div_a_kk = A[j, k] / A[k, k] 
        for i=j:n
            A[i, j] -= A[i, k] * a_jk_div_a_kk    # L_22
        end
    end
    sqrt_akk = sqrt(A[k, k])
    for i=k:n
        A[i, k] /= sqrt_akk    # l_11 and b
    end
end

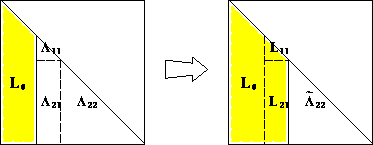
Source: http://www.netlib.org

• Computational cost:

plus $n$ square roots. Half the cost of LU decomposition.

• In general Cholesky decomposition is very stable. Failure of the decomposition simply means $\mathbf{A}$ is not positive definite. It is an efficient way to test positive definiteness.

Pivoting¶

• Pivoting is only needed if you want the Cholesky factor of a positive semidefinite matrix.

• When $\mathbf{A}$ does not have full rank, e.g., $\mathbf{X}^T \mathbf{X}$ with a non-full column rank $\mathbf{X}$, we encounter $a_{kk} = 0$ during the procedure.

• Symmetric pivoting. At each stage $k$, we permute both row and column such that $\max_{k \le i \le n} a_{ii}$ becomes the pivot. If we encounter $\max_{k \le i \le n} a_{ii} = 0$, then $\mathbf{A}[k:n,k:n] = \mathbf{0}$ (why?) and the algorithm terminates.

• With symmetric pivoting:

where $\mathbf{P}$ is a permutation matrix and $\mathbf{L} \in \mathbb{R}^{n \times r}$, $r = \text{rank}(\mathbf{A})$.

Implementation¶

• LAPACK functions: ?potrf (without pivoting), ?pstrf (with pivoting).

• Julia functions: cholesky, cholesky!, or call LAPACK wrapper functions potrf! and pstrf!

Example: positive definite matrix¶

Example: positive semidefinite matrix¶

Applications¶

• No inversion mentality: Whenever we see matrix inverse, we should think in terms of solving linear equations. If the matrix is positive (semi)definite, use Cholesky decomposition, which is twice cheaper than LU decomposition.

Multivariate normal density¶

Multivariate normal density $\mathcal{N}(0, \Sigma)$, where $\Sigma$ is $n\times n$ positive definite, is $$ \frac{1}{(2\pi)^{n/2}\det(\Sigma)^{1/2}}\exp\left(-\frac{1}{2}\mathbf{y}^T\Sigma^{-1}\mathbf{y}\right). $$

Hence the log likelihood is $$

• \frac{n}{2} \log (2\pi) - \frac{1}{2} \log \det \Sigma - \frac{1}{2} \mathbf{y}^T \Sigma^{-1} \mathbf{y}.

$$

• Method 1:

  1. compute explicit inverse $\Sigma^{-1}$ ($2n^3$ flops),
  2. compute quadratic form ($2n^2 + 2n$ flops),
  3. compute determinant ($2n^3/3$ flops).

• Method 2:

  1. Cholesky decomposition $\Sigma = \mathbf{L} \mathbf{L}^T$ ($n^3/3$ flops),
  2. Solve $\mathbf{L} \mathbf{x} = \mathbf{y}$ by forward substitutions ($n^2$ flops),
  3. compute quadratic form $\mathbf{x}^T \mathbf{x}$ ($2n$ flops)
  4. compute determinant from Cholesky factor ($n$ flops).

Which method is better?

• To evaluate same multivariate normal density at many observations $y_1, y_2, \ldots$, we pre-compute the Cholesky decomposition ($n^3/3$ flops), then each evaluation costs $n^2$ flops.

Linear regression by Cholesky¶

• Cholesky decomposition is one approach to solve linear regression. Assume $\mathbf{X} \in \mathbb{R}^{n \times p}$ and $\mathbf{y} \in \mathbb{R}^n$.
  • Compute $\mathbf{X}^T \mathbf{X}$: $np^2$ flops
  • Compute $\mathbf{X}^T \mathbf{y}$: $2np$ flops
  • Cholesky decomposition of $\mathbf{X}^T \mathbf{X}$: $\frac{1}{3} p^3$ flops
  • Solve normal equation $\mathbf{X}^T \mathbf{X} \beta = \mathbf{X}^T \mathbf{y}$: $2p^2$ flops
  • If need standard errors, another $(4/3)p^3$ flops

Total computational cost is $np^2 + (1/3) p^3$ (without s.e.) or $np^2 + (5/3) p^3$ (with s.e.) flops.

Further reading¶

• Section 7.7 of Numerical Analysis for Statisticians of Kenneth Lange (2010).

• Section II.5.3 of Computational Statistics by James Gentle (2010).

• Section 4.2 of Matrix Computation by Gene Golub and Charles Van Loan (2013).

Acknowledgment¶

Many parts of this lecture note is based on Dr. Hua Zhou's 2019 Spring Statistical Computing course notes available at http://hua-zhou.github.io/teaching/biostatm280-2019spring/index.html.