versioninfo()
Julia Version 1.9.3 Commit bed2cd540a1 (2023-08-24 14:43 UTC) Build Info: Official https://julialang.org/ release Platform Info: OS: macOS (x86_64-apple-darwin22.4.0) CPU: 8 × Intel(R) Core(TM) i5-8279U CPU @ 2.40GHz WORD_SIZE: 64 LIBM: libopenlibm LLVM: libLLVM-14.0.6 (ORCJIT, skylake) Threads: 2 on 8 virtual cores
using Pkg
Pkg.activate(pwd())
Pkg.instantiate()
Pkg.status()
Activating project at `~/Dropbox/class/M1399.000200/2023/M1300_000200-2023fall/lectures/17-qp`
Status `~/Dropbox/class/M1399.000200/2023/M1300_000200-2023fall/lectures/17-qp/Project.toml` [1e616198] COSMO v0.8.8 [f65535da] Convex v0.15.4 [a93c6f00] DataFrames v1.6.1 [2e9cd046] Gurobi v1.2.0 [b99e6be6] Hypatia v0.7.3 [b6b21f68] Ipopt v1.5.1 [b8f27783] MathOptInterface v1.22.0 [6405355b] Mosek v10.1.3 [1ec41992] MosekTools v0.15.1 [91a5bcdd] Plots v1.39.0 [c946c3f1] SCS v2.0.0
Quadratic programming (QP)¶
 {width=500}
{width=500}
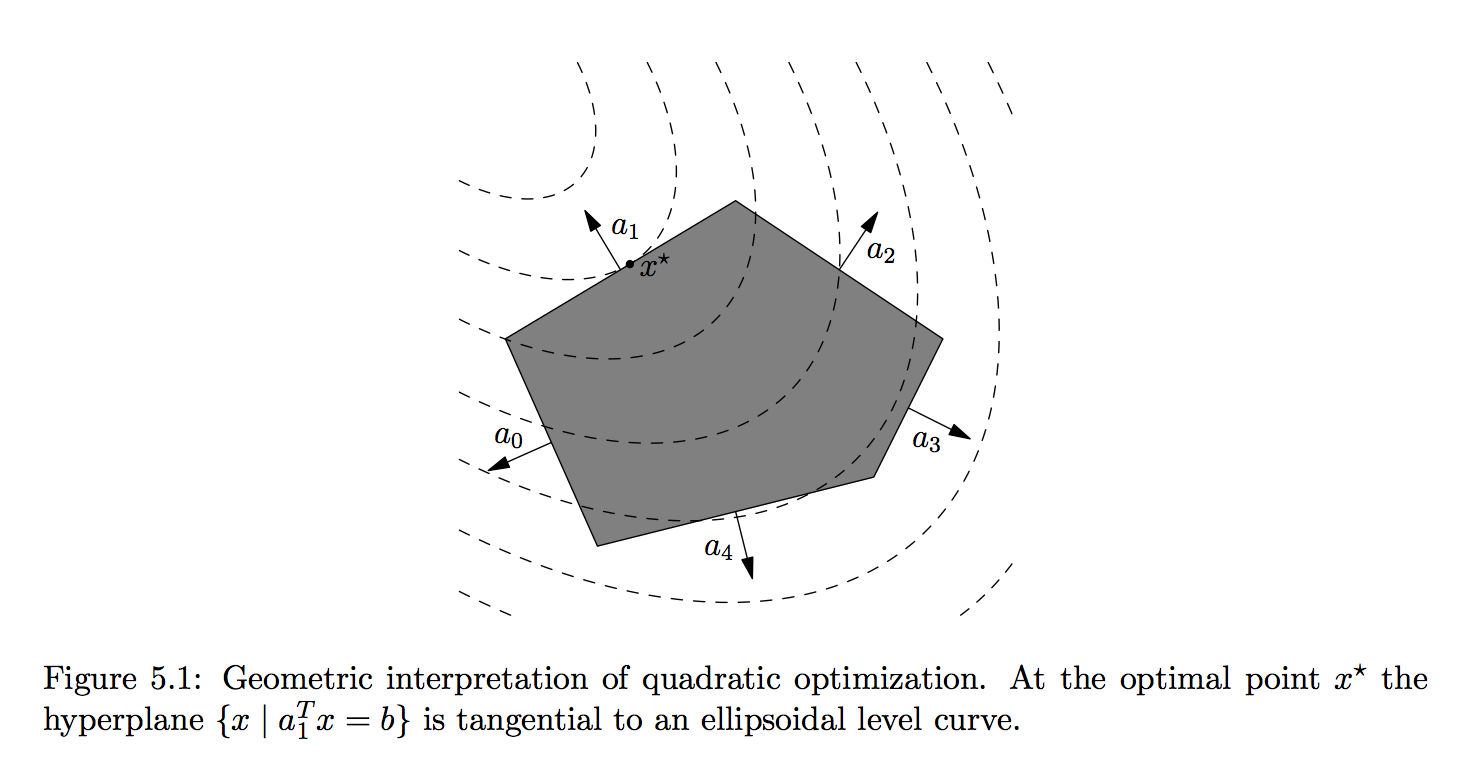
- A (linearly constrained) quadratic program (QP) has quadratic objective function and affine constraint functions
where we require $\mathbf{P} \in \mathbb{S}_+^d$ (why?). Apparently LP is a special case of QP with $\mathbf{P} = \mathbf{0}_{n \times n}$.
Example 1: least squares¶
- The least squares problem minimizes $\|\mathbf{y} - \beta_0\mathbf{1} - \mathbf{X} \beta\|_2^2$, which obviously is an (unconstrained) QP.
+ If the data is centered ($\mathbf{1}^T\mathbf{X} = \mathbf{0}$), then $\beta_0 = \frac{1}{n}\mathbf{y}$.
- Ridge regression.
+ $\mathbf{P} = \mathbf{X}^T\mathbf{X} + \lambda \mathbf{I} \in \mathbb{S}_{++}^d$
+ Usually the intercept $\beta_0$ is not penalized.
+ If the data is centered ($\mathbf{1}^T\mathbf{X} = \mathbf{0}$), then $\beta_0 = \frac{1}{n}\mathbf{y}$. (Why?)
using Statistics
using Random, LinearAlgebra, SparseArrays
Random.seed!(123) # seed
n, p = 100, 10
# Design matrix
X0 = randn(n, p)
X = [ones(n, 1) (X0 .- mean(X0 ,dims=1)) ./ std(X0, dims=1)] # design matrix is standardized and includes intercept
# True regression coefficients (first 5 are non-zero)
β = [1.0; randn(5); zeros(p - 5)]
# Responses
y = X * β + randn(n)
# plot the true β
using Plots
plt = plot(1:p, β[2:end], line=:stem, marker=2, legend=:none)
xlabel!(plt, "coordinate")
ylabel!(plt, "beta_j")
title!(plt, "True beta")
[ Info: Precompiling IJuliaExt [2f4121a4-3b3a-5ce6-9c5e-1f2673ce168a]
using Convex, MathOptInterface
using Mosek, MosekTools
const MOI = MathOptInterface
# solve at a grid of λ
λgrid = 0:20:1000
ridgepath = zeros(length(λgrid), size(X, 2)) # each row is β̂ at a λ
β̂ridge = Variable(size(X, 2))
@time for i in 1:length(λgrid)
λ = λgrid[i]
# objective
problem = minimize(sumsquares(y - X * β̂ridge) + λ * sumsquares(β̂ridge[2:end]))
solver = Mosek.Optimizer() # MOSEK this time!
MOI.set(solver, MOI.RawOptimizerAttribute("LOG"), 0) # keep silent
solve!(problem, solver)
ridgepath[i, :] = β̂ridge.value
end
plt = plot(collect(λgrid), ridgepath, legend=:none)
xlabel!(plt, "lambda")
ylabel!(plt, "beta_hat")
title!(plt, "Ridge")
1.251917 seconds (807.74 k allocations: 66.132 MiB, 1.98% gc time, 71.62% compilation time)
Example 2: constrained least squares¶
- Least squares with linear constraints. For example, nonnegative least squares (NLS)
# Use COSMO solver
using COSMO
solver = COSMO.Optimizer()
## Use SCS solver
# using SCS
# solver = SCS.Optimizer()
## Use Mosek solver
# using Mosek, MosekTools
# solver = Mosek.Optimizer()
## Use Hypatia solver
# using Hypatia
# solver = Hypatia.Optimizer()
# Set up optimizaiton problem
β̂nonneg = Variable(size(X, 2))
problem = minimize(0.5sumsquares(y - X * β̂nonneg))
problem.constraints += β̂nonneg[2:end] >= 0
# Solve the problem
@time solve!(problem, solver)
------------------------------------------------------------------
COSMO v0.8.8 - A Quadratic Objective Conic Solver
Michael Garstka
University of Oxford, 2017 - 2022
------------------------------------------------------------------
Problem: x ∈ R^{14},
constraints: A ∈ R^{116x14} (1116 nnz),
matrix size to factor: 130x130,
Floating-point precision: Float64
Sets: SecondOrderCone of dim: 101
Nonnegatives of dim: 11
SecondOrderCone of dim: 3
ZeroSet of dim: 1
Settings: ϵ_abs = 1.0e-05, ϵ_rel = 1.0e-05,
ϵ_prim_inf = 1.0e-04, ϵ_dual_inf = 1.0e-04,
ρ = 0.1, σ = 1e-06, α = 1.6,
max_iter = 5000,
scaling iter = 10 (on),
check termination every 25 iter,
check infeasibility every 40 iter,
KKT system solver: QDLDL
Acc: Anderson Type2{QRDecomp},
Memory size = 15, RestartedMemory,
Safeguarded: true, tol: 2.0
Setup Time: 0.51ms
Iter: Objective: Primal Res: Dual Res: Rho:
1 -2.4722e+00 7.6016e+00 6.0000e-01 1.0000e-01
25 6.3747e+01 2.0829e+00 8.8559e-01 1.0000e-01
50 2.1884e+02 9.9949e-01 4.4922e-02 1.0000e-01
75 2.1529e+02 8.2760e-01 1.2783e-02 1.0000e-01
100 4.4454e+02 7.3353e-01 3.9757e-02 8.2846e-03
125 3.6790e+02 3.2831e-01 8.5896e-01 1.1684e-03
150 3.9757e+02 4.0840e-01 4.2608e-04 1.1684e-03
175 3.8432e+02 3.5502e-01 2.1204e-05 1.1684e-03
200 3.8269e+02 3.4818e-01 5.6533e+00 7.7739e-03
225 3.7135e+02 2.8675e-01 1.4084e-03 7.7739e-03
250 3.8831e+02 2.7539e-01 9.8296e-05 7.7739e-03
275 4.0925e+02 1.8601e-01 3.1028e-04 7.7739e-03
300 4.2158e+02 2.0524e-01 3.1091e-04 7.7739e-03
325 4.2877e+02 1.8994e-01 3.4531e-05 7.7739e-03
350 4.3495e+02 1.4451e-01 6.2244e-04 7.7739e-03
375 4.3518e+02 1.6097e-01 2.8631e-04 7.7739e-03
400 4.4218e+02 1.6236e-01 3.0478e-04 7.7739e-03
425 4.6533e+02 1.5223e-01 5.9527e-04 7.7739e-03
450 4.8040e+02 1.1258e-01 8.7138e-05 7.7739e-03
475 4.7379e+02 9.0149e-02 8.9405e-05 7.7739e-03
500 4.7549e+02 8.7159e-02 4.2263e-05 7.7739e-03
525 4.8306e+02 7.6308e-02 4.9924e-06 7.7739e-03
550 4.8484e+02 7.3429e-02 7.9817e-05 7.7739e-03
575 5.0510e+02 1.0148e-01 3.5214e-03 7.7739e-03
600 5.0488e+02 5.2970e-02 2.7751e-04 7.7739e-03
625 5.1273e+02 2.1994e-02 2.1870e-04 7.7739e-03
650 5.1248e+02 1.8134e-02 4.3111e-05 7.7739e-03
675 5.1440e+02 1.2543e-02 1.5382e-05 7.7739e-03
700 5.1657e+02 1.4869e-02 6.1672e-05 7.7739e-03
725 5.1786e+02 1.0807e-02 1.0758e-05 7.7739e-03
750 5.1774e+02 1.0375e-02 6.7655e-06 7.7739e-03
775 5.1798e+02 1.0285e-02 1.2674e-05 7.7739e-03
------------------------------------------------------------------
>>> Results
Status: Solved
Iterations: 831 (incl. 56 safeguarding iter)
Optimal objective: 518
Runtime: 0.019s (19.35ms)
0.037223 seconds (24.25 k allocations: 5.272 MiB, 22.73% compilation time)
plot(β[2:end], line=:stem, label="true beta")
plot!(β̂nonneg.value[2:end], line=:stem, title="Nonnegative LS", label="fitted")
Example 3: lasso¶
- Lasso regression Tibshirani (1996), Donoho (1994) minimizes the least squares loss with $\ell_1$ (lasso) penalty
where $\lambda \ge 0$ is a tuning parameter. Writing $\beta = \beta^+ - \beta^-$, the equivalent QP is $$ \small \begin{array}{ll} \text{minimize}& \frac 12 (\beta^+ - \beta^-)^T \mathbf{X}^T \left(\mathbf{I} - \frac{\mathbf{1} \mathbf{1}^T}{n} \right) \mathbf{X} (\beta^+ - \beta^-) + \mathbf{y}^T \left(\mathbf{I} - \frac{\mathbf{1} \mathbf{1}^T}{n} \right) \mathbf{X} (\beta^+ - \beta^-) + \lambda \mathbf{1}^T (\beta^+ + \beta^-) \\ \text{subject to}& \beta^+ \geq \mathbf{0}, \, \beta^- \geq \mathbf{0} \end{array} $$ in $\beta^+$ and $\beta^-$; $\mathbf{x} = (\beta^+, \beta^-)$.
using Mosek, MosekTools
# solve at a grid of λ
λgrid = 0:10:200
β̂path = zeros(length(λgrid), size(X, 2)) # each row is β̂ at a λ
β̂lasso = Variable(size(X, 2))
@time for i in 1:length(λgrid)
λ = λgrid[i]
# objective
problem = minimize(0.5sumsquares(y - X * β̂lasso) + λ * norm(β̂lasso[2:end], 1))
solver = Mosek.Optimizer() # MOSEK this time!
MOI.set(solver, MOI.RawOptimizerAttribute("LOG"), 0) # keep silent
solve!(problem, solver)
β̂path[i, :] = β̂lasso.value
end
plt = plot(collect(λgrid), β̂path, legend=:none)
xlabel!(plt, "lambda")
ylabel!(plt, "beta_hat")
title!(plt, "Lasso")
17.769835 seconds (21.27 M allocations: 1.975 GiB, 4.78% gc time, 97.45% compilation time)
Example 4: elastic net¶
- Elastic net Zou and Hastie (2005)
where $\lambda \ge 0$ and $\alpha \in [0,1]$ are tuning parameters.
# solve at a grid of λ
λgrid = 0:10:400
alpha = 0.5
elastipath = zeros(length(λgrid), size(X, 2)) # each row is β̂ at a λ
β̂elastic = Variable(size(X, 2))
@time for i in 1:length(λgrid)
λ = λgrid[i]
# objective
problem = minimize(0.5*sumsquares(y - X * β̂elastic) +
λ * (alpha*norm(β̂elastic[2:end],1) + (1-alpha)*sumsquares(β̂elastic[2:end])))
solver = Mosek.Optimizer() # MOSEK this time!
MOI.set(solver, MOI.RawOptimizerAttribute("LOG"), 0) # keep silent
solve!(problem, solver)
elastipath[i, :] = β̂elastic.value
end
plt = plot(collect(λgrid), elastipath, legend=:none)
xlabel!(plt, "lambda")
ylabel!(plt, "beta_hat")
title!(plt, "Elastic net")
0.366815 seconds (491.97 k allocations: 42.703 MiB, 31.14% compilation time)
QP example 5: constrained lasso¶
- (Linearly) constrained lasso
where $\lambda \ge 0$ is a tuning parameter.
- We have seen this example (zero-sum lasso) before.
using Mosek, MosekTools
# solve at a grid of λ
λgrid = 0:10:150
β̂conpath = zeros(length(λgrid), size(X, 2)) # each row is β̂ at a λ
β̂conlasso = Variable(size(X, 2))
@time for i in 1:length(λgrid)
λ = λgrid[i]
# objective
problem = minimize(0.5sumsquares(y - X * β̂conlasso) + λ * norm(β̂conlasso[2:end], 1))
problem.constraints += β̂conlasso[2:end] >= 0
solver = Mosek.Optimizer() # MOSEK this time!
MOI.set(solver, MOI.RawOptimizerAttribute("LOG"), 0) # keep silent
solve!(problem, solver)
β̂conpath[i, :] = β̂conlasso.value
end
plt = plot(collect(λgrid), β̂conpath, legend=:none)
xlabel!(plt, "lambda")
ylabel!(plt, "beta_hat")
title!(plt, "Constrained Lasso")
0.115292 seconds (120.25 k allocations: 11.904 MiB)
QP example 7: robust regression¶
- The Huber loss function
is commonly used in robust statistics. The robust regression problem \begin{eqnarray*} &\text{minimize}& \sum_{i=1}^n \phi(y_i - \beta_0 - \mathbf{x}_i^T \beta) \end{eqnarray*} can be transformed to a QP \begin{eqnarray*} &\text{minimize}& \mathbf{u}^T \mathbf{u} + 2 M \mathbf{1}^T \mathbf{v} \\ &\text{subject to}& - \mathbf{u} - \mathbf{v} \leq \mathbf{y} - \mathbf{X} \beta \leq \mathbf{u} + \mathbf{v} \\ & & \mathbf{0} \leq \mathbf{u} \leq M \mathbf{1}, \mathbf{v} \geq \mathbf{0} \end{eqnarray*} in $\mathbf{u}, \mathbf{v} \in \mathbb{R}^n$ and $\beta \in \mathbb{R}^p$. Hint: write $|r_i| = (|r_i| \wedge M) + (|r_i| - M)_+ = u_i + v_i$.

QP example 8: SVM¶
- In two-class classification problems, we are given training data $(\mathbf{x}_i, y_i)$, $i=1,\ldots,n$, where $\mathbf{x}_i \in \mathbb{R}^n$ are feature vector and $y_i \in \{-1, 1\}$ are class labels. Support vector machine (SVM) solves the optimization problem
where $\lambda \ge 0$ is a tuning parameters. This is a QP (why?).
# convert to classification problem
Y = sign.(X * β + 5 * randn(n))
# solve at a grid of λ
λgrid = 0:10:100
β̂svmpath = zeros(length(λgrid), size(X, 2)) # each row is β̂ at a λ
β̂svm = Variable(size(X, 2))
@time for i in 1:length(λgrid)
λ = λgrid[i]
# objective
problem = minimize(sum(pos(1 - Y .* (X * β̂svm))) + λ * sumsquares(β̂svm[2:end]))
solver = Mosek.Optimizer() # MOSEK this time!
MOI.set(solver, MOI.RawOptimizerAttribute("LOG"), 0) # keep silent
solve!(problem, solver)
β̂svmpath[i, :] = β̂svm.value
end
plt = plot(collect(λgrid), β̂svmpath, legend=:none)
xlabel!(plt, "lambda")
ylabel!(plt, "beta_hat")
title!(plt, "SVM")
1.881291 seconds (2.51 M allocations: 167.199 MiB, 4.83% gc time, 93.43% compilation time)