Overfitting and Model Selection¶
This notebook will show
- the process of dividing train/test/validation sets
- an example of overfitting
- an example of estimator complexity
Input data¶
import pandas as pd
import sklearn.datasets as datasets
X, y = datasets.make_circles(n_samples=2000, factor=0.2, noise=0.24, random_state=42)
# X, y = datasets.make_blobs(n_samples=2000, cluster_std=1.0, random_state=0) # another dataset to try
# X, y = datasets.make_moons(n_samples=2000, noise=0.3, random_state=0) # another dataset to try
df_train = pd.DataFrame({"x0": X[:, 0], "x1": X[:, 1], "y": y})
df_train.plot.scatter(
x="x0", y="x1", c="y",
cmap="tab10", alpha=1.0,
vmax=10, colorbar=False, figsize=(4, 4),
)
<AxesSubplot:xlabel='x0', ylabel='x1'>
How does the model behave?¶
This section only gathers intuition on how the model behaves. It does not select the best performing model.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=0)
from sklearn.tree import DecisionTreeClassifier
max_depth = 8
clf = DecisionTreeClassifier(max_depth=max_depth, random_state=42)
clf.fit(X_train, y_train)
DecisionTreeClassifier(max_depth=8, random_state=42)
Let's visualize the decision region:
# This cell produces a grid of points, that covers the full dataset
# Don't worry about the syntax for now!
import numpy as np
x0 = np.linspace(df_train["x0"].min(), df_train["x0"].max())
x1 = np.linspace(df_train["x1"].min(), df_train["x1"].max())
x0, x1 = np.meshgrid(x0, x1)
df_test = pd.DataFrame({"x0": x0.flat[:], "x1": x1.flat[:]})
y_pred = clf.predict(df_test[["x0", "x1"]])
df_test["prediction"] = y_pred
df_test.plot.scatter(
x="x0", y="x1", c="prediction", cmap="tab10", vmax=10, colorbar=False, figsize=(4, 4)
)
<AxesSubplot:xlabel='x0', ylabel='x1'>
Evaluate the accuracy of the classifier (predict on the test set)
y_pred = clf.predict(X_test)
from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_pred)
0.945
It looks like the choice of max_depth could be a little better; the model looks to be a little rough around the edges.
Choosing max_depth¶
Let's choose the best max_depth. One rule to keep in mind:
Do not test the model on any data used to train.
Or, said a different way,
Only use the test data once at the very end
That means that all hyperparameter selection should be performed with the train dataset.
Let's wrap the above code used to get intuition on the classifier into a function. This will be done two different ways:
- Using a manual train/test split.
- Using a fancier method that provides some niceties
The nicer function will make it less clear what's happening, but offers a more robust scoring process.
Using train_test_split¶
Let's understand the process. What data is used for the model selection process?
def max_depth_info(X_train, y_train, max_depth=4):
"""
Find the best depth for DecisionTreeClassifier.
This function should take the train data
(which is why "_train" appended to input names).
Because training data should never be used for testing,
it splits the input data one more time into dataset for
training and validation.
Returns
-------
dictionary with keys "max_depth", "train_accuracy", "val_accuracy".
"""
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.2, random_state=0)
clf = DecisionTreeClassifier(max_depth=max_depth, random_state=42)
clf.fit(X_train, y_train)
val_score = clf.score(X_val, y_val)
# This is only to compare with val_score
train_score = clf.score(X_train, y_train)
return {"max_depth": max_depth,
"train_accuracy": train_score,
"val_accuracy": val_score}
The function train_test_split splits a dataset into two parts. See the documentation: https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html
Using cross_val_score¶
This is a fancier method that has a more robust scoring process. Specifically, it'll hopefully be robust to any imbalances in the training dataset. See the documentation for more detail: https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html
k-fold cross validation is defined as a process that...
- splits the data into $k$ chunks
- for $i = 1, ..., k$,
- $k - 1$ chunks are used for training
- $1$ chunk is used for testing
Then, a list of scores of length $k$ is returned.
from sklearn.model_selection import cross_val_score
def max_depth_info(X_train, y_train, max_depth=4):
"""
This is function is very slightly different than the previous definition:
It has the same inputs and outputs.
However, it uses Scikit-Learn's `cross_val_score` instead of
the manual train_test_split. This means that this function trains
and scores 5 different models. The "validation score" is defined to
be the mean of these 5 different scores.
"""
clf = DecisionTreeClassifier(max_depth=max_depth, random_state=42)
clf.fit(X_train, y_train)
scores = cross_val_score(clf, X, y, cv=5)
return {"max_depth": max_depth,
"train_accuracy": clf.score(X_train, y_train),
"val_accuracy": scores.mean()}
Remember the rule: do not test the model on any data used to train. What if the model just memorizes the training points?
More information is at https://scikit-learn.org/stable/modules/cross_validation.html. This page has a clear depiction of how the train/test set is split:
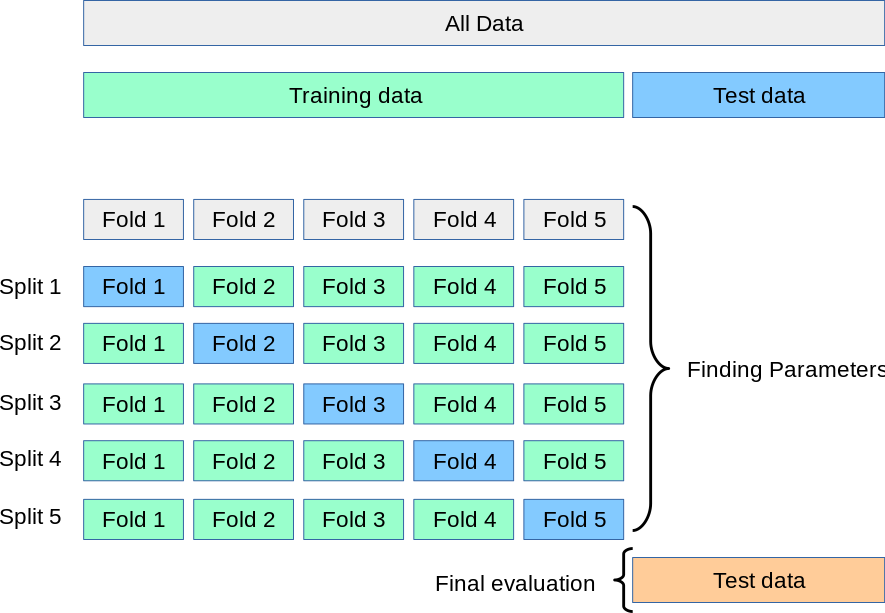
Now, let's call that function repeatedly to see
data = [max_depth_info(X_train, y_train, max_depth=k)
for k in range(1,15)]
df = pd.DataFrame(data)
ax = df.plot(x="max_depth", y=["train_accuracy", "val_accuracy"], style="o-", grid=True)
df.head(8)
| max_depth | train_accuracy | val_accuracy | |
|---|---|---|---|
| 0 | 1 | 0.655556 | 0.6240 |
| 1 | 2 | 0.800000 | 0.7915 |
| 2 | 3 | 0.868333 | 0.8580 |
| 3 | 4 | 0.940000 | 0.9330 |
| 4 | 5 | 0.945000 | 0.9285 |
| 5 | 6 | 0.953333 | 0.9225 |
| 6 | 7 | 0.958889 | 0.9195 |
| 7 | 8 | 0.967778 | 0.9150 |
Let's find the highest val_accuracy in this dataframe, then pull out the best depth from that:
best_row = df.val_accuracy.idxmax()
best_depth = df.loc[best_row]["max_depth"]
df.loc[best_row]
max_depth 4.000 train_accuracy 0.940 val_accuracy 0.933 Name: 3, dtype: float64
Looks like max_depth=4 is the best hyper-parameter. Let's train a model with max_depth=4, and test it to see the accuracy:
clf = DecisionTreeClassifier(max_depth=best_depth)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
0.945
Questions¶
What data should given as input to the hyper-parameter optimization process? i.e., what's the input to
get_best_depthbelow?X, y = pd.read_csv(...) X_train, X_test, y_train, y_test = train_test_split(X, y) max_depth = get_best_depth(...) # what goes here? print(max_depth) # prints "4" clf = DecisionTreeClassifier(max_depth=max_depth) clf.fit(X_train, y_train) clf.score(X_test, y_test)
- Input: the train data.
- Input: the test data.
- Input: the test and train data.
- Input: only the (untrained) model. The best hyper-parameters only depend on the model.
Why shouldn't the same dataset be used to train a model and evaluate performance of that model?
(the data used to train a model is the "train data", and the data used to evaluate the performance is the "test data")
- Because the model has seen the training data before. What if the model just memorized the answers for the training data?
- Because the model's goal is to perform well on unseen data. The best way to do that is train on one dataset and test on another.
- Because the model's goal is to perform well on unseen data. Why would testing on data it's already seen before be a good evaluation of that goal?
- It's okay to train on the test data because of "big data" and with the underlying algorithms.
Rerun this notebook for the two other datasets in the first cell. Which one has prodces the largest gap between "train_accuracy" and "val_accuracy" in the plot? (either definition of
get_max_depth_scorecan be used)
- make_circles dataset
- make_blobs dataset
- make_moons dataset